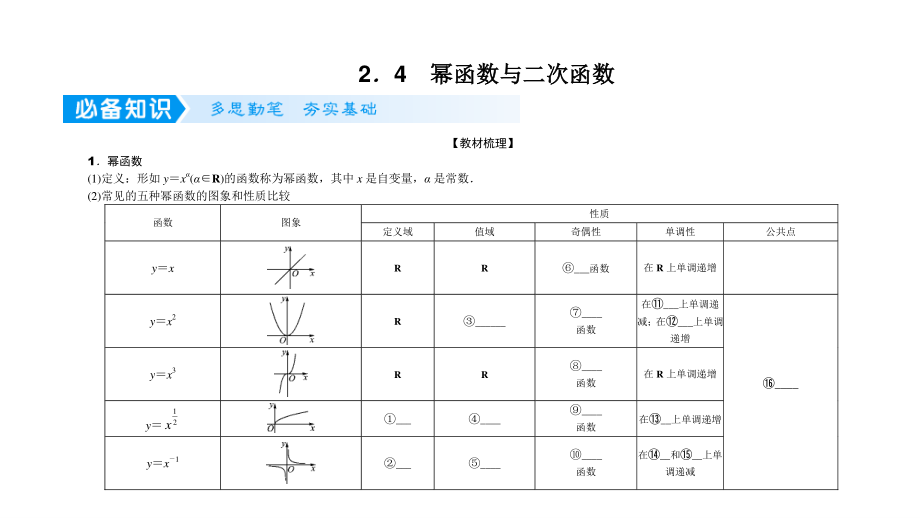
1、24 幂函数与二次函数幂函数与二次函数 【教材梳理】 1幂函数 (1)定义：形如 yx(R)的函数称为幂函数，其中 x 是自变量， 是常数 (2)常见的五种幂函数的图象和性质比较 性质 函数 图象 定义域 值域 奇偶性 单调性 公共点 yx R R _函数 在 R 上单调递增 yx2 R _ _ 函数 在_上单调递 减；在_上单调 递增 yx3 R R _ 函数 在 R 上单调递增 y 2 1 x _ _ _ 函数 在_上单调递增 yx 1 _ _ _ 函数 在_和_上单 调递减 _ 2二次函数解析式的三种形式 (1)一般式：f(x)_ (a0) (2)顶点式：f(x)_ (a0) (3)零点
2、式：f(x)_ (a0) 3二次函数的图象与性质 二次函数 f(x)ax2bxc(a0)的图象是一条抛物线，它的对称轴、顶点坐标、开口方向、 值域、单调性分别是： (1)对称轴：x_ (2)顶点坐标：_ (3)开口方向：a0 时，开口；a0 时，开口 (4)值域：a0 时，y_，a0 时，y_ (5)单调性：a0 时，f(x)在上是减函数，在上是增函数；a0 时，f(x)在 ， b 2a 上是， 在 b 2a， 上是_ 4二次函数、二次方程、二次不等式三者之间的关系 二次函数 f(x)ax2bxc(a0)的零点(图象与 x 轴交点的横坐标)是相应一元二次 方程 ax2bxc0 的，也是一元二次
3、不等式 ax2bxc0(或 ax2bxc0)解集的 5二次函数在闭区间上的最值 二次函数在闭区间上必有最大值和最小值 它只能在区间的或二次函数的处取得，可分别求值再比较大小，最后确定最值 【常用结论】 6幂函数相关常用结论 (1)一般地，在区间(0，1)上，幂函数中指数越大，函数图象越靠近 x 轴(简记为“指 大、图低”)，在区间(1，)上，幂函数中指数越大，图象越远离 x 轴(不包括幂函数 y x0) (2)幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出 现在第二、三象限内，则要看函数的定义域和奇偶性函数的图象最多只能同时出现在 两个象限内，如果幂函数的图象与坐标轴相
4、交，则交点一定是原点 (3)形如 yx m n或 y m n x (m，n 为互质的正整数)类型函数的奇偶性判断：当 m，n 都 为奇数时，幂函数在定义域上为奇函数；当 m 为奇数，n 为偶数时，幂函数在定义域上 为非奇非偶函数；当 m 为偶数，n 为奇数时，幂函数在定义域上为偶函数 7二次函数相关常用结论 对于二次函数 f(x)ax2bxc(a0)： (1)|a|越大，抛物线开口越小；|a|越小，抛物线开口越大 (2)f(1)abc，f(1)abc，f(0)c (3)|AB|x1x2| |a| （x1x2）24x1x2，其中 A(x1，0)，B(x2，0)为二次 函数与 x 轴的交点 8一元
5、二次方程根的分布 设 x1，x2是实系数一元二次方程 ax2bxc0(a0)的两实根，则 x1，x2的 分布范围与系数之间的关系如表所示 根的分布 (mnp 且 m， n，p 均为常数) 图象 满足的条件 x1x2m 0， b 2a0. mx1x2 0， b 2am， f（m）0. x1mx2 f(m)0， m b 2a0， f（n）0. mx1nx2p f（m）0， f（n）0. mx1x2n 0， m b 2an. 只有一根在区间(m，n)内 f(m) f(n)0. 【自查自纠】 1x|x0 x|x0 y|y0 y|y0 y|y0 奇 偶 奇 非奇非偶 奇 (，0 0，) 0，) (，0)
6、 (0，) (1，1) 2(1)ax2bxc (2)a(xh)2k (3)a(xx1)(xx2) 3(1) b 2a (2) b 2a， 4acb2 4a (3)向上 向下 (4) 4acb2 4a ， ，4acb 2 4a (5) ， b 2a b 2a， 增函数 减函数 4根 端点值 5端点 顶点 判断下列命题是否正确，正确的在括号内画“”，错误的画“” (1)函数 y3x 3 是幂函数 ( ) (2)二次函数 yax2bxc，xa，b的最值一定是4acb 2 4a ( ) (3)二次函数 yax2bxc，xR 不可能是偶函数 ( ) (4)如果幂函数的图象与坐标轴相交，则交点一定是原点
7、( ) (5)当 n0即可，解 得 0a1 4故填 0，1 4 考点一考点一 幂函数的图象和性质幂函数的图象和性质 (1)已知幂函数 yf(x)的图象过点 1 2， 2 2 ，则 log2f(2)的值为 ( ) A1 2 B 1 2 C1 D1 解：由题可得：设 f(x)xa，因为 f(x)的图象过点(1 2， 2 2 )，故(1 2) a 2 2 a1 2， 所以 f(x)x 1 2，故 log2f(2)log22 1 21 2故选 A (2)(2020内蒙古宁城高一期末)已知函数 yxa，yxb，yxc的部分图象如图所示， 则 a，b，c 的大小关系为( ) Acba Babc Cbca
8、Dca1，0b1，c(3x1) 2 3的解为( ) A 1 3，1 B(1，0) C(0，1) D(，0)(1，) 解：(x1) 2 3(3x1) 2 3等价于3 （x1）2 3 （3x1）2，所以(x1)2(3x1)2， 解得1x0 时，图象过原点和(1，1)，在第一象 限的图象上升；当 0，且 m1)的图象所经过的定点，则 b 的值等于( ) A1 2 B 2 2 C2 D2 解：由于 g(x)(2a1)xa 1 为幂函数，则 2a11，解得 a1，所以 g(x)x2当 x b 时，f(b)mb b1 2 1 2 ，故 f(x)的图象所经过的定点为 b，1 2 ，所以 g(b)1 2，即
9、b 21 2， 解得 b 2 2 故选 B (2)幂函数 y 2 4mm x (mZ)的图象如图所示，则 m 的值为( ) A0 B1 C2 D3 解：因为 y 2 4mm x (mZ)的图象不过原点，所以 m24m0，即 0m4又因为函数的图象关于 y 轴对称且 mZ，所以 m24m 为偶数， 因此 m2故选 C (3)已知 a2 4 3，b3 2 3，c25 1 3，则 ( ) Abac Babc Cbca Dcaab故选 A 考点二考点二 求二次函数的解析式求二次函数的解析式 (1)已知二次函数 f(x)满足 f(2)1，f(1)1，且 f(x)的最大值是 8， 则二次函数的解析式为_
10、解法一：(利用一般式) 设 f(x)ax2bxc(a0)， 由题意得 4a2bc1， abc1， 4acb2 4a 8， 解得 a4， b4， c7 所以所求二次函数为 y4x24x7 解法二：(利用顶点式) 设 f(x)a(xm)2n(a0)，因为 f(2)f(1)， 所以抛物线对称轴为 x2（1） 2 1 2， 所以 m1 2，又根据题意，函数有最大值为 8，所以 n8， 所以 f(x)a x1 2 2 8 因为 f(2)1，即 a 21 2 2 81解之得 a4 所以 f(x)4 x1 2 2 84x24x7 解法三：(利用零点式) 由已知 f(x)10 的两根为 x12，x21，即 g
11、(x)f(x)1 的两个零点为 2，1， 故可设 f(x)1a(x2)(x1)(a0)， 即 f(x)ax2ax2a1 又函数有最大值 ymax8，即4a（2a1）a 2 4a 8， 解之得 a4， 所以所求函数解析式为 f(x)4x24x2(4)14x24x7故填 f(x)4x2 4x7 (2)已知二次函数 f(x)的二次项系数为 a，且不等式 f(x)2x 的解集为(1， 3)若方程 f(x)6a0 有两个相等的根，则 f(x)的解析式为_ 解：因为 f(x)2x0 的解集为(1，3)， 设 f(x)2xa(x1)(x3)，且 a0， 所以 f(x)a(x1)(x3)2xax2(24a)x
12、3A 则方程 f(x)6a0，即 ax2(24a)x9a0 因为方程有两个相等的根，所以 (24a)24a9a0，解得 a1 或 a 1 5 由于 a0，所以 a1 5，代入式得 f(x) 1 5x 26 5x 3 5，即为所求故填 f(x) 1 5x 26 5x 3 5 【点拨】 根据已知条件确定二次函数的解析式，一般用待定系数法，方法如下： (1)二次函数的图象过点(0，1)，对称轴为 x2，最小值为1， 则它的解析式是 y_ 解：设 ya(x2)21(a0)， 当 x0 时，4a11，a1 2， 所以 y1 2(x2) 211 2x 22x1 故填1 2x 22x1 (2)若函数 f(x
13、)(xa)(bx2a)(常数 a，bR)是偶函数，且它的值域为(， 4，则该函数的解析式 f(x)_ 解：因为 f(x)的值域为(，4，所以 a0，b0，由 f(x)是偶函数知 f(x)的图 象关于 y 轴对称，所以a2a b 0，b2，所以 f(x)2x22a2，又 f(x)的值域 为(，4，所以 2a24，故 f(x)2x24故填2x24 (3)已知二次函数 yf(x)的图象经过点(4，3)，它在 x 轴上截得的线段长 为 2，并且对任意 xR，都有 f(2x)f(2x)，则 f(x)_ 解：因为 f(2x)f(2x)对任意 xR 恒成立，所以 f(x)图象的对称轴为 x2 又因为 f(x
14、)的图象被 x 轴截得的线段长为 2，所以 f(x)0 的两根为 1 和 3 设 f(x)的解析式为 f(x)a(x1)(x3)(a0)，又 f(x)的图象过点(4，3)，所以 3a 3，a1， 所以所求 f(x)的解析式为 f(x)(x1)(x3)， 即 f(x)x24x3故填 x24x3 考点三考点三 二次函数的图象与性质二次函数的图象与性质 命题角度 1 二次函数的图象 【多选题】如图是二次函数 yax2bxc 图象的一部分，图象过点 A(3，0)， 对称轴为 x1则下面四个结论中正确的是 ( ) Ab24ac B2ab1 Cabc0 D5ab 解：因为图象与 x 轴交于两点，所以 b2
15、4ac0，即 b24ac，A 正确；对称轴 为 x1，即 b 2a1，2ab0，B 错误；结合图象，当 x1 时，y0，即 abc0，C 错误；由对称轴为 x1 知，b2a，又函数图象开口向下，所以 a0，所以 5a2a，即 5ab，D 正确故选 AD 【点拨】 对于函数 f(x)ax2bxc，若是二次函数，就隐含 a0，当题 目未说明是二次函数时，就要分 a0 和 a0 两种情况讨论；在二次函数 y ax2bxc(a0)中，a 的正负决定抛物线开口的方向(a 的大小决定开口大小)，c 确定抛物线在 y 轴上的截距，b 与 a 确定顶点的横坐标(或对称轴的位置) 抛物线 yax2bxc 的顶点
16、在第一象限，与 x 轴的两个交点分别位于原点两侧， 则 a，b，c 的符号为( ) Aa0，b0，c0 Ba0，b0，c0 Ca0，b0，c0 Da0，b0，c0 解：由题意知抛物线开口向下，故 a0由抛物线与 x 轴的两个交点分别位 于原点两侧得c a0 再由顶点在第一象限得 b 2a0，所以 b0 故选 B 命题角度 2 二次函数的单调性 若函数 f(x)x22ax3 在区间4，6上是单调函数，则实数 a 的 取值范围为_ 解：由于函数 f(x)的图象开口向上，对称轴是 xa，所以要使 f(x) 在4，6上是单调函数，应有a4 或a6，即 a6 或 a4故 填(，64，) 【点拨】 二次函
17、数的单调性由其图象开口方向及对称轴位置确 定， 故而若是二次项系数含参数， 则往往还需要讨论其正负(开口方 向) 如果函数 f(x)ax22x3 在区间(，4)上是单调递增的， 则实数 a 的取值范围是 ( ) A 1 4， B 1 4， C 1 4，0 D 1 4，0 解： 当 a0 时， 函数 f(x)2x3 为一次函数， 在(， 4)上单调递增； 当 a0 时，依题意知，a0 且对称轴1 a4，解得 a 1 4，又 a0，故 1 4a0综上， 1 4 a0故选 D 命题角度 3 二次函数的最值 (1)若函数 f(x)x23x4 的定义域为0，m， 值域为 25 4 ，4 ， 则 m 的取
18、值范围是_ 解：函数 f(x)图象的对称轴为 x3 2，且 f 3 2 25 4 ，f(3)f(0)4，由二 次函数的图象知 m 的取值范围为 3 2，3 故填 3 2，3 (2)已知函数 f(x)x22ax1a 在区间0，1上的最大值为 2，则 a 的值为( ) A2 B1 或3 C2 或3 D1 或 2 解：函数 f(x)x22ax1a 图象的对称轴为直线 xa，开口向下 当 a0 时，f(x)在区间0，1上是减函数，所以 f(x)maxf(0)1a，由 1a2， 得 a1； 当 0a1 时，f(x)在区间0，a上是增函数，在a，1上是减函数，所以 f(x)maxf(a) a22a21aa
19、2a1， 由 a2a12， 解得 a1 5 2 或 a1 5 2 ， 因为 01 时，f(x)在区间0，1上是增函数，所以 f(x)maxf(1)12a1a2，所 以 a2 综上可知，a1 或 a2故选 D 【点拨】 二次函数在闭区间上的最值主要有三种类型：轴定区间定、 轴动区间定、轴定区间动不论哪种类型，解题的关键都是对称轴与区间 的位置关系，当含有参数时，要依据对称轴与区间的位置关系进行分类讨 论要注意数形结合思想的应用， 尤其是给定区间上的二次函数最值问题， 先“定性”(作草图)，再“定量”(看图求解)，事半功倍 (1)若函数 f(x)x22x1 在区间a，a2上的最小值为 4，则 a
20、的 取值集合为 ( ) A3，3 B1，3 C3，3 D1，3，3 解：函数 f(x)x22x1(x1)2，其图象的对称轴方程为 x1 因为 f(x)在区间a，a2上的最小值为 4， 令 x22x14x1 或 3 令 a21 或 a3，得 a3 或 3， 故 a 的取值集合为3，3故选 C (2)(20192020学年陕西安康高一上期中)定义在 R 上的偶函数 f(x)满足：当 x(，0时，f(x)x2mx1 ()当 x0 时，f(x)的解析式为_； ()若函数 f(x)在区间2，4上的最大值为 4，则 m 的值为_ 解：()当 x0 时，x0，f(x)x2mx1 因为 f(x)为偶函数，所以
21、 f(x)f(x)x2mx1(x0) ()当m 2 2，即 m4 时，f(x)在2，4上递减，所以 f(2)42m14，m9 2，不符合； 当 2m 2 4，即8m4 时，m 2 4 14，m2 5，此时 m2 5； 当m 2 4，即 m8 时，f(x)在2，4上递增， 所以 f(4)164m14，m21 4 ，不符合 综上可得 m2 5 故填()f(x)x2mx1；()2 5 命题角度 4 二次方程根的分布 已知关于 x 的二次方程 x22mx2m10 (1)若方程有两根，其中一根在区间(1，0)内，另一根在区间(1，2)内，求 m 的取值范围； (2)若方程两根均在区间(0，1)内，求 m
22、 的取值范围 解：(1)条件说明抛物线 f(x)x22mx2m1 与 x 轴的交点分别在区间(1，0) 和(1，2)内，作出函数 f(x)的大致图象，得 f（0）2m10， f（1）4m20 m 1 2， mR， m5 6 所以5 6m0， f（1）4m20， （2m）24（2m1）0， 0m 1 2， m1 2， m1 2或m1 2， 1m0 所以1 2m1 2 故 m 的取值范围为 m|1 2m1 2 【点拨】 对一元二次方程根的问题的研究，主要分三个方面：根 的个数问题，由判别式判断；正负根问题，由判别式及韦达定理判断； 根的分布问题，依函数与方程思想，通过考查开口方向、对称轴、判 别式
23、、端点函数值等数形结合求解 (1)(2020安徽省临泉一中高一月考)二次方程x2(a21)xa 20 有一个根比 1 大，另一个根比1 小，则 a 的取值范围是( ) A(2，0) B(1，0) C(3，1) D(0，2) 解：设 f(x)x2(a21)xa2， 因为二次方程 x2(a21)xa20，有一个根比 1 大，另一个根比1 小，所以 f(x)的图象与 x 轴的交点横坐标一个比 1 大，另一个比1 小，又抛物线开口向上，所以 f（1）0， f（1）0， 解得1a0， f（1）0， 即 42bc0， 1bc0， 即 2bc4， bc1， 又 f(3)93bc， 令 3bcm(2bc)n(
24、bc)，则 2mn3， nm1， 解得 m4， n5， 故 3bcm(2bc)n(bc)445(1)11， 所以 f(3)20 又 c0 且 cb1，故 b10，即 b1，所以 3bc3，即 f(3)12 综上知 f(3)的取值范围是(12，20)故选 C 命题角度 5 二次函数中的恒成立问题 (1)已知 a 是实数，函数 f(x)2ax22x3 在 x1，1上恒小于 零，则实数 a 的取值范围是_ 解：2ax22x30 在1，1上恒成立当 x0 时，30，成立；当 x0 时，a3 2 1 x 1 3 2 1 6，因为 1 x(，11，)，当 x1 时，右边 取最小值1 2， 所以 a0(a0
25、) 恒成立的充要条件为 a0， 0，f(x)0(a0)恒成立的充要条件为 a0， 0 (1)已知 f(x)x22(a2)x4，如果对 x3，1，f(x)0 恒 成立，则实数 a 的取值范围为_ 解：因为 f(x)x22(a2)x4，对称轴 x(a2)，对 x3，1，f(x)0 恒成立， 所以讨论对称轴与区间3，1的位置关系得： （a2）3， f（3）0， 或 3（a2）1， 0， 或 （a2）1， f（1）0， 解得 a或 1a4 或1 2a1，所以 a 的取值范围为 1 2，4 故填 1 2，4 (2)设 f(x)是定义在 R 上的偶函数， 且当 x0 时， f(x)2x若对任意的 xa， a2，不等式 f(xa)f(x)2恒成立，则实数 a 的取值范围是_ 解：由题知函数 f(x)2|x|，故 f(xa)f(x)2，即 2|x a|(2|x|)222|x|，即|xa|2|x|， 即 3x22axa20 对任意的 xa，a2恒成立令 g(x)3x22axa2，则只要 g(a)0 且 g(a2)0 即可g(a)0，满足要求，g(a2)3(a2)22a(a2)a28a120， 即 a3 2故填 ，3 2
