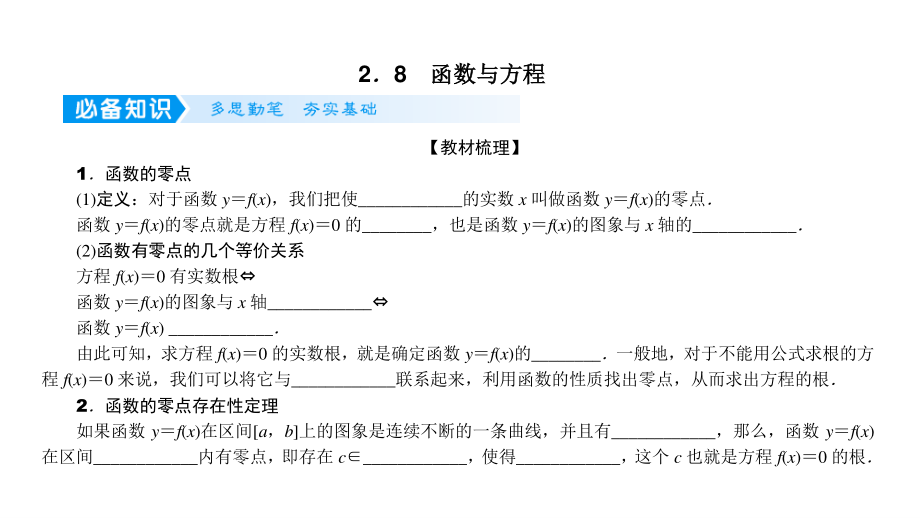
1、28 函数与方程函数与方程 【教材梳理】 1函数的零点 (1)定义：对于函数 yf(x)，我们把使_的实数 x 叫做函数 yf(x)的零点 函数 yf(x)的零点就是方程 f(x)0 的_，也是函数 yf(x)的图象与 x 轴的_ (2)函数有零点的几个等价关系 方程 f(x)0 有实数根 函数 yf(x)的图象与 x 轴_ 函数 yf(x) _ 由此可知，求方程 f(x)0 的实数根，就是确定函数 yf(x)的_一般地，对于不能用公式求根的方 程 f(x)0 来说，我们可以将它与_联系起来，利用函数的性质找出零点，从而求出方程的根 2函数的零点存在性定理 如果函数 yf(x)在区间a，b上的
2、图象是连续不断的一条曲线，并且有_，那么，函数 yf(x) 在区间_内有零点，即存在 c_，使得_，这个 c 也就是方程 f(x)0 的根 【常用结论】 3对于零点存在性定理，须知满足条件的零点可能不惟一；不满足条件时， 也可能有零点 4确定函数 f(x)零点个数的基本思路 (1)判断二次函数 f(x)在 R 上的零点个数， 一般由对应的二次方程 f(x)0 的判别 式 0，0，0 来完成；对于一些不便用判别式判断零点个数的二次函数， 则要结合二次函数的图象进行判断 (2)对于一般函数零点个数的判断，不仅要用到零点存在性定理，有时还必须结 合函数的图象和性质才能确定，如三次函数的零点个数问题
3、(3)若函数f(x)在a， b上的图象是连续不断的一条曲线， 且是单调函数， 又f(a) f(b) 0，则 yf(x)在区间(a，b)内有唯一零点 【自查自纠】 1(1)f(x)0 实数根 交点的横坐标 (2)有交点 有零点 零点 函数 yf(x) 2f(a) f(b)0 (a，b) (a，b) f(c)0 判断下列命题是否正确，正确的在括号内画“” ，错误的画“” (1)函数的零点就是函数的图象与 x 轴的交点( ) (2)函数 yf(x)在区间(a，b)内有零点(函数图象连续不断)，则 f(a) f(b)0 ( ) (3)只要函数有零点，我们就可以用二分法求出零点的近似值 ( ) (4)二
4、次函数 yax2bxc(a0)在 b24ac0 时没有零点 ( ) (5)已知函数 f(x)在a，b内图象连续且单调，若 f(a) f(b)0，则函数 f(x)在a，b上有 且只有一个零点( ) 解：(1)； (2)； (3)； (4)； (5) 下列函数的图象均与 x 轴有交点，其中不宜用二分法求交点横坐标的是( ) A B C D 解：利用二分法求函数与 x 轴交点的横坐标，该函数的零点必须是变号零点，所 以根据这个条件可知，不宜用二分法求交点横坐标的是选项 C 的图象故选 C (2020 合肥市第八中学高一月考)若函数 f(x)2xx7 的零点所在的区间 为(k，k1)(kZ)，则 k(
5、 ) A3 B4 C1 D2 解：因为 f（2）4270，且 f(x)单调递增，所以 f(x)的零点所在的区间 为(2，3)，所以 k2故选 D (2018全国卷)已知函数 f(x) ex，x0， lnx，x0，g(x)f(x)xa若 g(x)存 在 2 个零点，则 a 的取值范围是( ) A1，0) B0，) C1，) D1，) 解：函数 g(x)f(x)xa 存在 2 个零点，即关于 x 的方程 f(x)xa 有 2 个 不同的实根，即函数 f(x)的图象与直线 yxa 有 2 个交点，作出直线 yxa 与函数 yf(x)的图象， 如图所示，由图可知，a1，解得 a1故选 C (2020
6、届湖北“荆、荆、襄、宜”四地七校高三上 10 月联考)函数 f(x) 3x2，x0， xlog36，x0的零点之和为_ 解：令 3x20，解得 xlog32，令 xlog360，解得 xlog36，则函数 f(x)的零点之和为 log32log36log31 31故填1 考点一考点一 判断函数零点所在区间判断函数零点所在区间 (1)函数 f(x)log8x 1 3x的一个零点所在的区间是 ( ) A(0，1) B(1，2) C(2，3) D(3，4) 解：因为函数 f(x)log8x 1 3x是连续的增函数，f(1)0 1 3 1 30，f(2) log821 6 1 3 1 60， 可得 f
7、(1)f(2)0， 所以函数 f(x)的零点所在的区间是(1， 2) 故 选 B (2)若 abc，则函数 f(x)(xa)(xb)(xb) (xc)(xc)(xa)的两 个零点分别位于区间 ( ) A(a，b)和(b，c)内 B(，a)和(a，b)内 C(b，c)和(c，)内 D(，a)和(c，)内 解： 易知 f(a)(ab)(ac)， f(b)(bc)(ba)， f(c)(ca)(cb)又 ab0，f(b)0，又该函数是二次函数，且图象开口向上，可知两个零 点分别位于区间(a，b)和(b，c)内故选 A 【点拨】 理解函数零点存在定理要注意三点： “函数 yf(x)在区间a，b上的图象是
8、一条连续不断的曲线”和“f(a)f(b)0)，则函数 yf(x)( ) A在区间(0，1)，(1，2)内均有零点 B在区间(0，1)内有零点，在区间(1，2)内无零点 C在区间(0，1)，(1，2)内均无零点 D在区间(0，1)内无零点，在区间(1，2)内有零点 解：f(x)1 xx 1x2 x ，故 f(x)在(0，1)上递增，在(1，)递减，又 f 1 e ln1 e 1 2 1 e 2 10，f(2)ln210 的零点个数为( ) A0 B1 C2 D3 解：由 x0， x22x30，得 x3由 x0， 2lnx0，得 xe 2所以 f(x)的零点个 数为 2故选 C (2)已知 f(x
9、) |lnx|，x0， 2|x|，x0， 则函数 y2f2(x)3f(x)1 的零点个数是_ 解：由 2f2(x)3f(x)10 得 f(x)1 2或 f(x)1， 作出函数 yf(x)的图象 由图象知 y1 2与 yf(x)的图象有 2 个交点，y1 与 yf(x)的图象有 3 个交点因此函 数 y2f2(x)3f(x)1 的零点有 5 个故填 5 (3)若定义在 R 上的偶函数 f(x)满足 f(x2)f(x)，当 x0，1时，f(x)x，则函 数 yf(x)log3|x|的零点个数是 ( ) A5 B4 C3 D2 解： 由题意知， f(x)是周期为 2 的偶函数在同一坐标系内作出函数
10、yf(x)及 ylog3|x| 的图象，如图 观察图象可以发现它们有 4 个交点，即函数 yf(x)log3|x|有 4 个零点故选 B 【点拨】 判断函数零点个数的方法：解方程法；零点存在性 定理结合函数的性质；数形结合法，即转化为两个函数图象的交点 个数 (1)函数 f(x)xcosx2在区间0，4上的零点个数为 ( ) A4 B5 C6 D7 解： 由 f(x)xcosx20， 得 x0 或 cosx20又 x0， 4， 所以 x20， 16由 于 cos 2k 0(kZ)，而在 2k(kZ)的所有取值中，只有 2， 3 2 ， 5 2 ， 7 2 ， 9 2 满足在0，16内，故零点个
11、数为 156故选 C (2)方程|x22x|a21(aR )的解的个数是 ( ) A1 B2 C3 D4 解：因为 aR ，所以 a211 而 y|x22x|的图象如图，所以 y|x22x| 的图象与 ya21 的图象总有两个交点所以方程有两解故选 B (3)已知 f(x)是定义在 R 上的奇函数，且当 x(0，)时，f(x)2 021xlog2 021x， 则函数 f(x)的零点个数是( ) A1 B2 C3 D4 解： 作出函数 y2 021x和 ylog2 021x 的图象如图所示， 可知函数 f(x)2 021x log2 021x 在 x(0，)上只有一个零点，又 f(x)是定义在
12、R 上的奇函数，所以 f(x) 在 x(，0)上只有一个零点，又 f(0)0，所以函数 f(x)的零点个数是 3故选 C 考点三考点三 函数零点的应用函数零点的应用 命题角度 1 由函数零点个数求参数 函数 f(x)2x2 xa 的一个零点在区间(1，2)内，则实数 a 的取值范围是( ) A(1，3) B(1，2) C(0，3) D(0，2) 解：因为函数 f(x)2x2 xa 在区间(1，2)上单调递增，又函数 f(x)2 x2 xa 的一 个零点在区间(1，2)内，则有 f(1)0 且 f(2)0，即 a0， 3a0， 所以 0a3故选 C 【点拨】 由零点存在性定理求参数范围，属于零点
13、存在性定理的逆用， 要注意结合函数的单调性来确定参数的范围，否则可能出错 若函数 f(x)3ax12a 在区间(1，1)上存在一个零点，则实 数 a 的取值范围是( ) A 1 5， B(，1) 1 5， C 1，1 5 D(，1) 解：显然 a0，因为 f(x)在(1，1)上为单调函数，要使函数 f(x)在区间(1， 1)上存在一个零点，则有 f(1)f(1)0，即(a1)(5a1)1 5或 a1 故 选 B 命题角度 2 与零点相关的比较大小问题 已知三个函数 f(x)2xx，g(x)x2，h(x)log2xx 的零点依次 为 a，b，c，则( ) Aabc Bacb Cbac Dcab
14、解：方法一：由于 f(1)1 21 1 20，且 f(x)为 R 上的单调递增函数，故 f(x) 的零点 a(1，0) 因为 g(2)0，所以 g(x)的零点 b2 因为 h 1 2 11 2 1 20，且 h(x)为(0，)上的增函数，所以 h(x)的零点 c 1 2，1 因此 acb 方法二：由 f(x)0 得 2xx，由 h(x)0 得 log2xx，作出函数 y2x，ylog2x 和 y x 的图象(如图) 由图象易知 a0，0c1，而 b2，故 acb故选 B 【点拨】 与函数零点有关的函数值比较大小， 可以通过函数性质结 合零点存在性定理确定，也可考虑在同一平面直角坐标系中画出图象
15、， 根据交点及图象位置关系确定 已知函数 f(x)|lg(x1)|ax(0a1)有两个零点 x1，x2，则有 ( ) Ax1x21 Bx1x2x1x2 解： 由已知得： 不妨设 1x1ax2ax2ax10 lg（x11）ax1， lg（x21）ax2 lg(x11)(x21)ax2ax10，化简得 x1x2x1x2故选 B 思想方法微专题 数形结合思想在函数与方程中的应用 (1)(2020天津卷)已知函数 f(x) x3，x0， x，x0， 1，x0， 当 k0 时，此时 y2，如图 1，y2 与 h(x)有 1 个不同交点，不满足题意； 图 1 当 k0 时，如图 3，当 ykx2 与 yx
16、2相切时，联立方程得 x2kx20， 图 3 令 0 得 k280，解得 k2 2(负值舍去)，所以 k2 2，此时直线 y|kx2|与 h(x)1(x0)无交点，满足题 意 综上，k 的取值范围为(，0)(2 2，)故选 D (2)设函数 f(x) 2xa，x1， 4（xa）（x2a），x1 ()若 a1，则 f(x)的最小值为_； ()若 f(x)恰有 2 个零点，则实数 a 的取值范围是_ 解：()若 a1，则 f(x) 2x1，x1， 4（x1）（x2），x1 作出函数 yf(x)的图象，如图所示由图可得 f(x)的最小值为1 ()当 a1 时，要使 f(x)恰有 2 个零点，需满足
17、21a0，即 a2，所以 a2当 a1 时，要使 f(x)恰有 2 个零点，需满足 a0， a0， 解得1 2a0， 若函数 g(x)f(x)xa 有 3 个零点， 则实数 a 的取值范围是( ) A0，2) B0，1) C(，2 D(，1 解：当 x0 时，f(x)3x22，易知 f(x)在(，0上先增后减，绘制出 f(x)的大致图 象如图，令 h(x)xa，则 h(x)与 f(x)的图象有三个交点， h(x)的图象介于 l1和 l2之间，l2过原点，则 a0，l1与 f(x)相切，则由 f(x)3x221， 得 x1(x1 舍去)，y1，代入 h(x)中，解得 a2，所以实数 a 的取值范围为0，2)故 选 A (2)(2019届北京市朝阳区高三二模)已知函数 f(x) 2x，xa， x，xa，若函数 f(x)存在零点， 则 实数 a 的取值范围是( ) A(，0) B(，1) C(1，) D(0，) 解：函数 f(x) 2x，xa， x，xa，的图象如图所示： 由于 2x0 恒成立，故若函数 f(x)存在零点，则必是 yx(xa)的零点，即 x0， 故实数 a 的取值范围是(0，)故选 D
