1、33 利用导数研究函数的极值、最值利用导数研究函数的极值、最值 【教材梳理】 1函数的极值与导数 (1)判断 f(x0)是极大值，还是极小值的方法 一般地，当 f(x0)0 时， 如果在 x0附近的左侧 f(x)0，右侧 f(x)0，那么 f(x0)是极大值； 如果在 x0附近的左侧_，右侧_，那么 f(x0)是极小值 (2)求可导函数极值的步骤 求 f(x) 求方程_的根 检查 f(x)在上述根的左右对应函数值的符号如果左正右负，那么 f(x)在这个根处取得 _；如果左负右正，那么 f(x)在这个根处取得_ 2函数的最值与导数 (1)在闭区间a，b上连续的函数 f(x)在a，b上必有最大值与
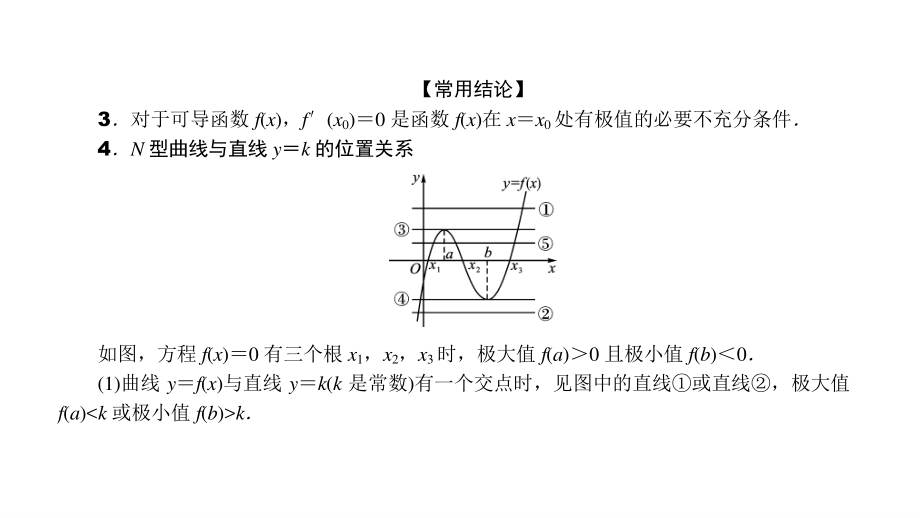
2、最小值 (2)若函数 f(x)在a，b上单调递增，则_为函数在a，b上的最小值， _为函数在a，b上的最大值；若函数 f(x)在a，b上单调递减，则为函数在 a，b上的最大值，_为函数在a，b上的最小值 (3)设函数 f(x)在a，b上连续，在(a，b)内可导，求 f(x)在a，b上的最大值和最小值的 步骤如下： 求 f(x)在(a，b)内的极值； 将 f(x)的各极值与端点处的函数值_，_进行比较，其中最大的一个是 _，最小的一个是_ 【常用结论】 3对于可导函数 f(x)，f(x0)0 是函数 f(x)在 xx0处有极值的必要不充分条件 4N 型曲线与直线 yk 的位置关系 如图，方程 f
3、(x)0 有三个根 x1，x2，x3时，极大值 f(a)0 且极小值 f(b)0 (1)曲线 yf(x)与直线 yk(k 是常数)有一个交点时，见图中的直线或直线，极大值 f(a)k (2)曲线 yf(x)与直线 yk(k 是常数)有两个交点时，见图中的直线或直 线，极大值 f(a)k 或极小值 f(b)k (3)曲线 yf(x)与直线 yk(k 是常数)有三个交点时，见图中的直线 5实际问题中的导数 (1)加速度是速度关于时间的导数 (2)线密度是质量关于长度的导数 (3)功率是功关于时间的导数 (4)瞬时电流是电荷量关于时间的导数 (5)水流的瞬时速度是流过的水量关于时间的导数 (6)边际
4、成本是成本关于产量的导数 【自查自纠】 1(1)f(x)0 f(x)0 (2)f(x)0 极大值 极小值 2(2)f(a) f(b) f(a) f(b) (3)f(a) f(b) 最大值 最小值 判断下列命题是否正确，正确的在括号内画“”，错误的画“” (1)函数的极大值不一定比极小值大 ( ) (2)对于可导函数 f(x)，f(x0)0 是 x0为极值点的充要条件 ( ) (3)函数的最大值不一定是极大值，函数的最小值也不一定是极小值 ( ) (4)函数 f(x)在(a，b)内单调，则函数 f(x)在(a，b)内一定没有极值 ( ) (5)三次函数在 R 上必有极大值和极小值 ( ) 解：(
5、1)； (2)； (3)； (4)； (5) (20192020学年江苏淮阴中学高二上10月考)函数 f(x)(x23x1)ex 的极大值为( ) Ae2 B5e 1 C5 4e 3 2 D2e 解：依题意，f(x)(x2x2)ex(x2)(x1)ex，故函数 f(x)在(，1)， (2，)上递增，在(1，2)上递减，所以函数 f(x)在 x1 处取得极大值为 f(1) 5e 1故选 B 设 f(x)是函数 f(x)的导函数， yf(x)的图象如图所示， 则 yf(x)的图象最有可能是 ( ) A B C D 解：由 f(x)的图象可知，x0 是函数 f(x)的极大值点，x 2 是 f(x)的
6、极小值点，仅选项 C 满足故选 C 函数 f(x)1 2xsinx 在 0， 2 上的最小值和最大值分别是( ) A 6 3 2 ，0 B 41，0 C 6 3 2 ， 41 D 1 2， 1 2 解：函数 f(x)1 2xsinx，f(x) 1 2cosx， 令 f(x)0，解得 2x 3； 令 f(x)0，解得 0 x 3， 所以 f(x)在 0， 3 递减，在 3， 2 递增， 所以 f(x)minf 3 6 3 2 ， 而 f(0)0， f 2 410， 故 f(x)在区间 0， 2 上 的最小值和最大值分别是 6 3 2 ，0故选 A 若 yalnxbx2x 在 x1 和 x2 处有
7、极值，则实数 a_， b_ 解：ya x2bx1由已知得 a2b10， a 24b10， 解得 a2 3， b1 6 故填2 3； 1 6 考点一考点一 利用导数解决函数的极值问题利用导数解决函数的极值问题 命题角度 1 由图象判断函数的极值 (1)(2020广西钦州高二期末)设三次函数 f(x)的导函数为 f(x)， 函数 yxf(x)的图象的一部 分如图所示，则下列判断正确的是 ( ) Af(x)的极大值为 f( 3)，极小值为 f( 3) Bf(x)的极大值为 f( 3)，极小值为 f( 3) Cf(x)的极大值为 f(3)，极小值为 f(3) Df(x)的极大值为 f(3)，极小值为
8、f(3) 解：由图象可知： 当 x3 和 x3 时，xf(x)0，则 f(3)f(3)0； 当 x0，则 f(x)0； 当3x0 时，xf(x)0； 当 0 x0，则 f(x)0； 当 x3 时，xf(x)0，则 f(x)0 所以 f(x)在(，3)上单调递减；在(3，0)，(0，3)上单调递增； 在(3，)上单调递减 所以 f(x)的极小值为 f(3)，极大值为 f(3)故选 C 【点拨】 由导函数图象判断函数 yf(x)的极值， 要抓住两点：由 y f(x)的图象与 x 轴的交点，可得函数 yf(x)的可能极值点；由导函数 y f(x)的图象可以看出 yf(x) 的值的正负，从而可得函数
9、yf(x)的单调性， 两者结合可得极值点 设函数 f(x)在 R 上可导，其导函数为 f(x)，且函数 y(1x)f(x)的图 象如图所示，则下列结论中一定成立的是( ) A函数 f(x)有极大值 f(2)和极小值 f(1) B函数 f(x)有极大值 f(2)和极小值 f(1) C函数 f(x)有极大值 f(2)和极小值 f(2) D函数 f(x)有极大值 f(2)和极小值 f(2) 解：由题图可知，当 x0；当2x1 时，f(x)0；当 1x2 时，f(x)2 时，f(x)0由此可以得到函数 f(x)在 x2 处取得极大 值，在 x2 处取得极小值故选 D 命题角度 2 求已知函数的极值 (
10、1)(2020届山东济钢高中高三上10月考)设函数 f(x)mxex3(mR)， 讨论函数 f(x)的极值 解：因为 f(x)mxex3，所以 f(x)mex， 当 m0 时，f(x)mex0 恒成立，因此 f(x)在 R 上单调递减，此时无极值； 当 m0 时，由 f(x)mex0 得 xlnm； 由 f(x)mex0 得 xlnm； 所以 f(x)在(， lnm)上单调递增， 在(lnm， )上单调递减， 因此 f(x)有极大值 f(lnm) mlnmm3 综上所述，当 m0 时，函数 f(x)无极值； 当 m0 时，f(x)有极大值 f(lnm)mlnmm3，无极小值 (2)已知函数 f
11、(x)x3ax2bxa2在 x1 处有极值 10，则 f(2)等于( ) A11 或 18 B11 C18 D17 或 18 解：因为函数 f(x)在 x1 处有极值 10， 所以 f(1)10，且 f(1)0， 即 1aba210， 32ab0， 解得 a3， b3 或 a4， b11 而当 a3，b3 时，f(x)3(x1)20，函数在 x1 处无极值，故舍去所以 f(x) x34x211x16，所以 f(2)18故选 C 【点拨】 求函数 f(x)极值的步骤：第一步，确定函数的定义域；第二步， 求导函数 f(x)；第三步，解方程 f(x)0，求出在函数定义域内的所有根；第四 步，列表检验
12、 f(x)在 f(x)0 的根 x0左右两侧值的符号，如果左正右负，那么 f(x)在 x0处取极大值，如果左负右正，那么 f(x)在 x0处取极小值 (1)(2020 贵州兴仁凤凰中学高二月考)已知函数 f(x)(x2mxm)ex 2m(mR，e 是自然对数的底数)在 x0 处取得极小值，则 f(x)的极大值是 ( ) A4e 2 B4e2 Ce2 De2 解：由题意知，f(x)x2(2m)x2mex， 由 f(0)2m0，解得 m0， 所以函数 f(x)x2ex，此时 f(x)(x22x) ex， 由 f(x)0，即 x22x0，解得 x0； 由 f(x)0，即 x22x0，解得2x0， x
13、1x21 a0， x1x2 1 2a0， 即 0a1 2故选 C 【点拨】 解含参数的极值问题要注意：f(x0)0 是 x0为函数极值点的 必要不充分条件，故而要注意检验；若函数 yf(x)在区间(a，b)内有极值， 那么 yf(x)在(a，b)内一定不是单调函数，反之，若函数在某区间上单调， 则函数没有极值 若函数 f(x)x 3 3 a 2x 2x1 在区间 1 2，3 上有极值点，则实数 a 的取值范围是( ) A 2，5 2 B 2，5 2 C 2，10 3 D 2，10 3 解： 若函数 f(x)在区间 1 2，3 上无极值点， 则当 x 1 2，3 时， f(x)0 恒成立或 f(
14、x)0 恒成立 当 x 1 2，3 时，yx 1 x 2，10 3 ；当 f(x)x2ax10 时，ax1 x恒成立，则 a2；当 f(x)x 2 ax1x1 x恒成立，则 a 10 3 因此要使函数 f(x)在 1 2，3 上有极值点，实数 a 的取值范围 是 2，10 3 另解：问题转化为 f(x)x2ax1 在 x 1 2，3 内存在变号零点，即 ax1 x，x 1 2，3 ， a240， 求值 域即可故选 C 考点二考点二 利用导数解决函数的最值问题利用导数解决函数的最值问题 命题角度 1 求函数最值 设函数 f(x)alnxbx2(x0)，若函数 f(x)在 x1 处与直线 y1 2
15、相切 (1)求实数 a，b 的值； (2)求函数 f(x)在 1 e，e 上的最大值 解：(1)f(x)a x2bx， 因为函数 f(x)在 x1 处与直线 y1 2相切， 所以 f（1）a2b0， f（1）b1 2， 解得 a1， b1 2 (2)由(1)知，f(x)lnx1 2x 2， f(x)1 xx 1x2 x ， 当1 exe 时，令 f(x)0，得 1 ex1， 令 f(x)0，得 1xe， 所以 f(x)在 1 e，1 上单调递增，在(1，e上单调递减， 所以 f(x)maxf(1)1 2 【点拨】 求函数 f(x)在a，b上的最大值和最小值的步骤：第一步，求函数 在(a，b)内
16、的极值；第二步，求函数在区间端点的函数值 f(a)，f(b)；第三步，将函 数 f(x)的极值与 f(a)，f(b)比较，其中最大的一个为最大值， 最小的一个为最小值 对于含参数的函数的最值，先讨论函数的单调性，再根据单调性求出最值含参函 数在区间上的最值通常有两类：一是动极值点定区间；二是定极值点动区间，这两 类问题一般根据区间与极值点的位置关系来分类讨论 (2019年广东潮州高二下质检)已知函数 f(x)(x22x)ex(xR，e 为自然对数的底数) (1)求函数 f(x)的单调区间； (2)求函数 f(x)在区间0，m上的最大值和最小值 解：(1)f(x)(x22x)ex，求导得 f(x
17、)ex(x22) 因为 ex0，令 f(x)ex(x22)0，即 x220，解得 x 2或 x 2 令 f(x)ex(x22)0，即 x220， 解得 2x 2 所以函数 f(x)在(， 2)和( 2，)上递增，在( 2， 2)上递减 即函数 f(x)的单调递增区间为(， 2)，( 2，)，单调递减区间为( 2， 2) (2)当 0m 2时，因为 f(x)在 2， 2上递减， 所以 f(x)在区间0，m上的最大值为 f(0)0， f(x)在区间0，m上的最小值为 f(m)(m22m)em 当 2m2 时， 因为 f(x)在 2， 2上递减，f(x)在 2，)上递增，且 f(0)f(2)0， 所
18、以 f(x)在0，m上的最大值为 f(0)0， f(x)在区间0，m上的最小值为 f( 2)(22 2)e 2 当 m2 时， 因为 f(x)在 2， 2上递减，f(x)在 2，)上递增，且 f(m)0f(0)， 所以 f(x)在0，m上的最大值为 f(m)(m22m)em，f(x)在区间0，m上的最小值为 f( 2) (22 2) e 2 命题角度 2 已知最值情况求参数范围 若函数 f(x)1 3x 3x22 3在区间(a，a5)上存在最小值，则实数 a 的取 值范围是_ 解：由题意得 f(x)x22xx(x2)，故 f(x)在(，2)，(0，)上是增函数， 在(2，0)上是减函数，作出其
19、图象如图所示 令1 3x 3x22 3 2 3得， x0 或 x3， 则结合图象可知， 3a0， 解得 a 3，0)故填3，0) 【点拨】 函数的图象和性质是解决函数最值问题的重要辅助手 段由于所给区间是开区间，故最值点不可能在区间端点处取得，进 而分析极值点与区间端点的关系即可 (2020届湖北宜昌高三9月考)函数 f(x)x33x 在区间(2，m)上有最大值， 则 m 的取值范围是_ 解：由于 f(x)3x233(x1)(x1)，故函数在(，1)和(1，)上递增，在( 1，1)上递减，f(1)f(2)2，画出函数图象如图所示， 由于函数在区间(2，m)上有最大值，根据图象可知 m(xB，x
20、A，即1m2故 填(1，2 考点三考点三 利用导数解决实际问题利用导数解决实际问题 如图，养殖公司欲在某湖边依托互相垂直的湖岸线 CA，CB 围成一个三角形养 殖区 ACB，为了便于管理，在线段 AB 之间有一观察站点 M，M 到直线 BC，CA 的距离 分别为 8 百米、1 百米，则观察点 M 到点 A，B 距离之和的最小值为_百米 解：以 C 为原点，CA，CB 所在直线分别作为 x，y 轴，建立平面直角坐标系，则 M(8，1)，设直线 AB：y1k(x 8)，即 ykx18k，则 A 18k k ，0 ，B(0，18k)，所以 18k k 0， 18k0， 所以 k0， AB2 18k
21、k 2 (18k)2f(k)(k0)， 则 f(k)(18k)2 1 1 k2 (k0)， 则 f(k)2(18k)(8) 1 1 k2 (18k)2(2) 1 k3 2（18k）（8k31） k3 k ，1 2 1 2 1 2，0 f(k) 0 f(k) 单调递减 极小 值 单调递增 所以当 k1 2时，AB 最短，此时 AB5 5故填 5 5 【点拨】 函数的优化问题即实际问题中的最值问题， 其一般解题 步骤为：一设，设出自变量、因变量；二列，列出函数关系式，并写 出定义域；三解，解出函数的最值，一般常用导数求解；四答，回答 实际问题 (2019年安徽黄山市屯溪一中高二下期中)某厂生产某种
22、产 品 x 件的总成本 C(x)1 200 1 27x 2(单位：万元)，又知产品单价的平 方与产品件数 x 成反比， 生产 100 件这样的产品单价为 50 万元， 则产 量定为_件时总利润最大 解：设产品单价为 m，因为产品单价的平方与产品件数 x 成反比，所以 m2k x(其中 k 为 非零常数)， 又生产 100 件这样的产品单价为 50 万元，所以 502 k 100，故 k250 000， 记生产 x 件产品时，总利润为 f(x)， 所以 f(x)mxC(x)500 x1 200 1 27x 2，x0， 则 f(x)250 x 2 27x， 由 f(x)0 得 0 x225，由 f(x)0 得 x225， 故函数 f(x)在(0，225)上单调递增，在(225，)上单调递减， 因此当 x225 时，f(x)取最大值即产量定为 225 件时，总利润最大故填 225
