1、93 随机事件的概率与古典概型随机事件的概率与古典概型 【教材梳理】 1随机事件和确定事件 (1)在条件 S 下，一定会发生的事件，叫做相对于条件 S 的_ (2)在条件 S 下，一定不会发生的事件，叫做相对于条件 S 的_ 必然事件与不可能事件统称为相对于一定条件 S 的确定事件 (3)在条件 S 下可能发生也可能不发生的事件，叫做相对于条件 S 的_ (4)_和_统称为事件，一般用大写字母 A，B，C，表示 2频率与概率 (1)在相同的条件 S 下重复 n 次试验，观察某一事件 A 是否出现，称 n 次试验中事件 A 出现的次数 nA 为事件 A 出现的_，称事件 A 出现的比例 fn(A
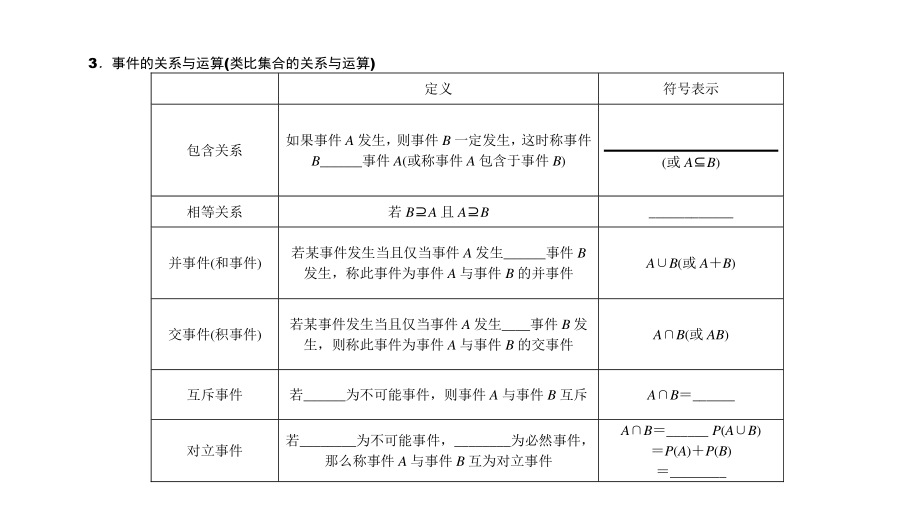
2、)_为事件 A 出现的频率 (2)对于给定的随机事件 A，如果随着试验次数的增加，事件 A 发生的_fn(A)稳定在某个常 数上，把这个_记作 P(A)，称为事件 A 的_ (3)在一次试验中几乎不可能发生的事件称为_ 3事件的关系与运算(类比集合的关系与运算) 定义 符号表示 包含关系 如果事件 A 发生， 则事件 B 一定发生， 这时称事件 B_事件 A(或称事件 A 包含于事件 B) (或 AB) 相等关系 若 BA 且 AB _ 并事件(和事件) 若某事件发生当且仅当事件 A 发生_事件 B 发生，称此事件为事件 A 与事件 B 的并事件 AB(或 AB) 交事件(积事件) 若某事件发
3、生当且仅当事件 A 发生_事件 B 发 生，则称此事件为事件 A 与事件 B 的交事件 AB(或 AB) 互斥事件 若_为不可能事件，则事件 A 与事件 B 互斥 AB_ 对立事件 若_为不可能事件，_为必然事件， 那么称事件 A 与事件 B 互为对立事件 AB_ P(AB) P(A)P(B) _ 4概率的几个基本性质 (1)概率的取值范围：_ (2)必然事件的概率 P(E)_ (3)不可能事件的概率 P(F)_ (4)互斥事件概率的加法公式 如果事件A与事件B互斥，则P(AB) _ 若事件B与事件A互为对立事件，则P(A) _ 5基本事件 在一次试验中，我们常常要关心的是所有可能发生的基本结
4、果，它们是试验中不能再分的 最简单的随机事件，其他事件可以用它们来描绘，这样的事件称为_ 6基本事件的特点 (1)任何两个基本事件是_的 (2)任何事件(除不可能事件)都可以表示成_的和 7古典概型 具有以下两个特点的概率模型称为古典概率模型，简称古典概型： (1)试验中所有可能出现的基本事件只有_个 (2)每个基本事件出现的可能性_ 8古典概型的概率公式 对于古典概型，其计算概率的公式为_ 【常用结论】 9如果事件 A1，A2，An两两互斥(彼此互斥)，那么事件 A1A2An 发生的概率，等于这 n 个事件分别发生的概率的和，即 P(A1A2An)P(A1) P(A2)P(An) 【自查自纠
5、】 1(1)必然事件 (2)不可能事件 (3)随机事件 (4)确定事件 随机事件 2(1)频数 nA n (2)频率 常数 概率 (3)小概率事件 3包含 BA AB 或 且 AB AB AB 1 4(1)0P(A)1 (2)1 (3)0 (4)P(A)P(B) 1P(B) 5基本事件 6(1)互斥 (2)基本事件 7(1)有限 (2)相等 8P(A)A包含的基本事件的个数 基本事件的总数 判断下列命题是否正确，正确的在括号内画“”，错误的画“” (1)事件发生的频率等于事件发生的概率 ( ) (2)P(AB)P(A)P(B) ( ) (3)若 A，B 为互斥事件，则 P(A)P(B)1( )
6、 (4)“在适宜条件下，种下一粒种子观察它是否发芽”属于古典概型，其基本事 件是“发芽与不发芽” ( ) (5)掷一枚硬币两次，出现“两个正面” “一正一反” “两个反面” ，这三个结果 是等可能事件 ( ) 解：(1)； (2)； (3)； (4)； (5) (2020安徽宣城期末)从装有 2 个红球和 2 个黑球的口袋内任取两个球， 那么互斥而不对立的事件是( ) A至少有一个黑球与都是黑球 B至少有一个黑球与至少有一个红球 C恰好有一个黑球与恰好有两个黑球 D至少有一个黑球与都是红球 解： 对于 A， “至少有一个黑球”等价于“一个黑球和一个红球或两个黑球”与 “都是黑球”可以同时发生，
7、不是互斥事件，故错误 对于 B， “至少有一个黑球” 等价于“一个黑球和一个红球或两个黑球”， “至 少有一个红球”等价于“一个黑球和一个红球或两个红球”，可以同时发生，故错 误 对于 C, “恰好有一个黑球” 等价于“一个黑球和一个红球”，与“恰好有两 个黑球”不同时发生，还有可能都是红球，不是对立事件，故正确 对于 D， “至少有一个黑球” 等价于“一个黑球和一个红球或两个黑球”，与 “都是红球”不同时发生，但一定会有一个发生，是对立事件，故错误故选 C 若有 2 位老师，2 位学生站成一排合影，则每位老师都不站在两端的概率是( ) A 1 12 B 1 6 C1 4 D 1 2 解：依题
8、意，所求概率为 PA 2 2A 2 2 A4 4 1 6故选 B (2021届湖北武汉起点质检)我国古人认为宇宙万物是由金、木、水、火、土这五种元 素构成，历史文献尚书 洪范提出了五行的说法，到战国晚期，五行相生相克的思想被正 式提出这五种物质属性的相生相克关系如图所示，若从这五种物质属性中随机选取三种， 则取出的三种物质属性中，彼此间恰好有一个相生关系和两个相克关系的概率为( ) A3 5 B 1 2 C2 5 D 1 3 解： 从 5 种物质属性中选 3 个有 C3 510 种情况， 其中恰好有一个相生关系和两个 相克关系，即图中有两个相邻，另一个与这两个都不相邻，有 5 种情况，所以所求
9、概 率为 P 5 10 1 2故选 B (2018全国卷)若某群体中的成员只用现金支付的概率 为 045，既用现金支付也用非现金支付的概率为 015，则不 用现金支付的概率为_ 解：设事件 A 为只用现金支付，事件 B 为只用非现金支付，事件 C 为既用现金支 付也用非现金支付，则 P(A)P(B)P(C)1，因为 P(A)045，P(C)015，所 以 P(B)04故填 04 考点一考点一 随机事件及其概率计算随机事件及其概率计算 命题角度 1 互斥、对立事件判断 (2020陕西商洛期末)将标有数字 3，4，5 的三张扑克牌随机分给甲、乙、丙三人， 每人一张，事件 A：“甲得到的扑克牌数字小
10、于乙得到的扑克牌数字”与事件 B：“乙得到 的扑克牌数字为 3”是 ( ) A互斥但不对立事件 B对立事件 C既不互斥又不对立事件 D以上都不对 解：依题意， 事件 A 为：(3，4)，(3，5)，(4，5)， 事件 B 为：(4，3)，(5，3)， 事件 A 与事件 B 不能同时发生，但能同时不发生， 所以事件 A 与事件 B 是互斥但不对立事件故选 A 【点拨】 互斥事件、对立事件的判定方法：(1)利用基本概念：互斥 事件是两个不可能同时发生的事件；对立事件首先是互斥事件，且必有一 个发生(2)利用集合的观点来判断： 设事件 A 与 B 所含的结果组成的集合分 别是 A，B，事件 A 与
11、B 互斥，即集合 AB；事件 A 与 B 对立，即 集合 AB，且 ABI(全集)，也即 AIB 或 BIA；对互斥事件 A 与 B 的和 AB，可理解为集合 AB“互斥事件”与“对立事件”的区别 及联系：两个事件 A 与 B 是互斥事件，有如下三种情况：若事件 A 发生， 则事件 B 就不发生；若事件 B 发生，则事件 A 就不发生；事件 A，B 都 不发生两个事件 A 与 B 是对立事件，仅有前两种情况因此，互斥未必对 立，但对立一定互斥 (2020陕西西安二模)2021 年某省新高考将实行“312”模式，即语 文、数学、外语必选，物理、历史二选一，政治、地理、化学、生物四选二，共有 12
12、 种选课模式某同学已选了物理，记事件 A：“他选择政治和地理”，事件 B： “他选择化学和地理”，则事件 A 与事件 B ( ) A是互斥事件，不是对立事件 B是对立事件，不是互斥事件 C既是互斥事件，也是对立事件 D既不是互斥事件，也不是对立事件 解：事件 A 与事件 B 不能同时发生，是互斥事件，他还可以选择化学和政治， 不是对立事件故选 A 命题角度 2 随机事件的频率与概率 某超市为了解顾客的购物量及结算时间等信息， 安排一名员工随机收集了在该超市购 物的 100 位顾客的相关数据，如下表所示 一次购物量 1 至 4 件 5 至 8 件 9 至 12 件 13 至 16 件 17 件及
13、以上 顾客数/人 x 30 25 y 10 结算时间/ (min/人) 1 15 2 25 3 已知这 100 位顾客中一次购物量超过 8 件的顾客占 55% (1)确定 x，y 的值，并估计顾客一次购物的结算时间的平均值； (2)求一位顾客一次购物的结算时间不超过 2 min 的概率(将频率视为概率) 解：(1)由已知得 25y1055，x3045，所以 x15，y20 该超市所有顾客一次购物的结算时间组成一个总体，所收集的 100 位顾客一次购物的结算时间可视为 总体的一个容量为 100 的简单随机样本，顾客一次购物的结算时间的平均值可用样本平均数估计，其估计 值为 11515302252
14、520310 100 19(min) (2)记 A 表示事件“一位顾客一次购物的结算时间不超过 2 min” ，A1，A2，A3分别表示事件“该顾客一 次购物的结算时间为 1 min” 、“该顾客一次购物的结算时间为 15 min” 、“该顾客一次购物的结算时间 为 2 min”将频率视为概率得 P(A1) 15 100 3 20，P(A2) 30 100 3 10，P(A3) 25 100 1 4 因为 AA1A2A3，且 A1，A2，A3是互斥事件， 所以 P(A)P(A1A2A3)P(A1)P(A2)P(A3) 3 20 3 10 1 4 7 10 故一位顾客一次购物的结算时间不超过 2
15、 min 的概率为 7 10 【点拨】 概率是频率的稳定值， 它从数量上反映了随机事件发生的可能性的大 小，它是频率的科学抽象当试验次数越来越多时，频率越趋近于概率求解 随机事件的概率的常用方法有两种：可用频率来估计概率；利用随机事件 A 包含的基本事件数除以基本事件总数，计算的方法有：列表法、列举法、树 状图法等 某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆 车的赔付结果统计如下： 赔付金额(元) 0 1 000 2 000 3 000 4 000 车辆数(辆) 500 130 100 150 120 (1)若每辆车的投保金额均为 2 800 元，估计赔付金额大于投保金
16、额的概率； (2)在样本车辆中，车主是新司机的占 10%，在赔付金额为 4 000 元的样本车辆中， 车主是新司机的占 20%，估计在已投保车辆中，新司机获赔金额为 4 000 元的概率 解： (1)设事件A表示“赔付金额为 3 000元”， 事件B表示“赔付金额为4 000 元”， 以频率估计概率得 P(A) 150 1 000015，P(B) 120 1 000012由表格知，赔付金额大 于投保金额即事件(AB)发生， 且 A、 B 互斥所以 P(AB)P(A)P(B)015012 027故赔付金额大于投保金额的概率为 027 (2)设事件 C 表示“投保车辆中新司机获赔 4 000 元”
17、，由已知，样本车辆中车主为 新司机的有 011 000100(辆)，而赔付金额为 4 000 元的车辆中，车主为新司机的有 0212024(辆)所以样本车辆中新司机车主获赔金额为 4 000 元的频率为 24 100 024因此，由频率估计概率得 P(C)024 命题角度 3 互斥事件、对立事件的概率计算 某医院一天派出医生下乡医疗，派出医生人数及其概率如下： 医生人数 0 1 2 3 4 5人及以上 概率 01 016 03 02 02 004 求：(1)派出医生至多是 2 人的概率； (2)派出医生至少是 2 人的概率 解：记事件 A：“不派出医生”，事件 B：“派出 1 名医生”，事件
18、C：“派出 2 名医生”，事件 D： “派出 3 名医生”，事件 E：“派出 4 名医生”，事件 F：“派出不少于 5 名医生” 因为事件 A，B，C，D，E，F 彼此互斥， 且 P(A)01，P(B)016，P(C)03，P(D)02，P(E)02，P(F)004 (1)“派出医生至多 2 人”的概率为 P(ABC)P(A)P(B)P(C)0101603056 (2)方法一：“派出医生至少 2 人”的概率为 P(CDEF)P(C)P(D)P(E)P(F)030202004074 方法二： “派出医生至少 2 人”与“派出医生至多 1 人”是对立事件， “派出医生至多 1 人”的概率 PP(A
19、)P(B)01016026， 所以“派出医生至少 2 人”的概率 P1P1026074 【点拨】 解决此类问题， 首先应根据互斥事件和对立事件的定义分析 是不是互斥事件或对立事件，再选择概率公式进行计算求复杂的互斥事 件的概率一般有两种方法：直接法，将所求事件的概率分解为一些彼此 互斥的事件的概率的和，运用互斥事件的概率加法公式计算；间接法， 先求此事件的对立事件的概率，再用公式 P(A)1P(A)求解，即用正难 则反的数学思想，特别是“至多”“至少”型问题，用间接法往往显得较 简便 某商场有奖销售活动中， 购满 100 元商品得 1 张奖券， 多购多得1 000 张奖券为一个开奖单位，设特等
20、奖 1 个，一等奖 10 个，二等奖 50 个设 1 张奖 券中特等奖、一等奖、二等奖的事件分别为 A，B，C，求： (1)P(A)，P(B)，P(C)； (2)1 张奖券的中奖概率； (3)1 张奖券不中特等奖且不中一等奖的概率 解：(1)P(A) 1 1 000，P(B) 10 1 000 1 100， P(C) 50 1 000 1 20 (2)1 张奖券中奖包含中特等奖、一等奖、二等奖设“1 张奖券中奖”这个事件为 M，则 MABC 因为 A，B，C 两两互斥， 所以 P(M)P(ABC)P(A)P(B)P(C) 1 1 000 1 100 1 20 61 1 000 故 1 张奖券的
21、中奖概率为 61 1 000 (3)设“1 张奖券不中特等奖且不中一等奖”为事件 N，则事件 N 与“1 张奖券中特等奖或中一等奖”为对立 事件， 所以 P(N)1P(AB)1( 1 1 000 1 100) 989 1 000 故 1 张奖券不中特等奖且不中一等奖的概率为 989 1 000 考点二考点二 古典概型古典概型 命题角度 1 列举基本事件求概率 (1)(2018全国卷)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成 果哥德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”，如 30723在不超 过 30 的素数中，随机选取两个不同的数，其和等于 30 的概率是 (
22、 ) A 1 12 B 1 14 C 1 15 D 1 18 解：不超过 30 的素数有 2，3，5，7，11，13，17，19，23，29，共 10 个，随 机选取两个不同的数，共有 C2 1045 种方法，因为 7231119131730， 所以随机选取两个不同的数， 其和等于 30 的有 3 种方法， 故概率为 3 45 1 15 故选 C (2)古代埃及人在进行分数运算时，只使用分子是 1 的分数，因此，分子是 1 的分 数叫做埃及分数(也称为单位分数)，如1 8， 1 15， 1 24， 1 100等都是埃及分数 现从1 2， 1 3， 1 4， 1 5 ， 1 6 这 5 个分数中
23、，找出 2 个不同的分数，则这两个埃及分数的和为 n1 n n1 n 为最简分数，且nN*，n2 的概率为_ 解： 利用列举法， 从 5 个埃及分数中， 随机抽取 2 个不同埃及分数的基本事件总数为 C2 510， 其中1 2 1 3 5 6， 1 2 1 4 3 4， 1 2 1 6 4 6 2 3， 1 3 1 6 3 6 1 2，其余的均不满足题意，故所求概率为 P 4 10 2 5故填 2 5 【点拨】 基本事件总数较少且无规律时， 常用列举法把所有基 本事件一一列出，列举要有规律，要做到不重复、不遗漏，可借助 “树状图”列举 (1)如图，在 A，B 两点间有 6 条网线并联，它们能通
24、过的最大信息量分别为 1， 1，2，2，3，4，现从中任取三条且使每条网线通过最大信息量，则选取的三条网线由 A 到 B 可通过的信息总量为 6 的概率是 ( ) A1 4 B 1 3 C1 2 D 2 3 解：设这 6 条网线从上到下分别是 a，b，c，d，e，f，任取 3 条有 C3 620 种不同的取法，选取的三条网线由 A 到 B 可通过的信息总量为 6 的取法有(a，b， f)，(a，c，e)，(a，d，e)，(b，c，e)，(b，d，e)，共 5 种不同的取法，所以选取 的三条网线由 A 到 B 可通过的信息总量为 6 的概率是 5 20 1 4故选 A (2)已知函数 f(x)2
25、x24ax2b2，若 a4，6，8，b3，5，7，则 该函数有两个零点的概率为_ 解：要使函数 f(x)2x24ax2b2有两个零点，即方程 x22axb20 有两个 实根，则 4a24b20，又 a4，6，8，b3，5，7，即 ab，而(a，b)的所 有取法共有 339(种)，其中满足 ab 的取法有(4，3)，(6，3)，(6，5)，(8，3)， (8，5)，(8，7)，共 6 种，所以所求的概率为6 9 2 3故填 2 3 命题角度 2 有放回抽样与无放回抽样 (1)(2019全国卷)我国古代典籍周易用“卦”描述万物的变化每一“重卦”由从下到上 排列的 6 个爻组成，爻分为阳爻“”和阴爻
26、“ ” ，下图就是一重卦在所有重卦中随机取一重卦， 则该重卦恰有 3 个阳爻的概率是 ( ) A 5 16 B 11 32 C21 32 D 11 16 解：所求概率为C 3 6 26 5 16故选 A (2)(2020河南信阳六中高三月考)某盒中装有产品 10 个，其中有 7 个正品，3 个次品 ()从中不放回地依次抽取 3 个产品，求取到的次品数比正品数多的概率； ()从中任取一个产品，若取出的是次品不放回，再取一个产品，直到取得正品为止， 求在取得正品之前已取出的次品数 X 的分布列和数学期望 解：()取到 3 个次品的概率 P1 C3 3 C3 10 1 120； 取到 2 个次品、1
27、 个正品的概率 P2 C1 7 C1 10 C1 3 C1 9 C1 2 C1 83 21 120故所求概率 PP1P2 1 120 21 120 11 60 ()由题意可得 X 的所有可能取值为 0，1，2，3 P(X0) C1 7 C1 10 7 10；P(X1) C1 3 C1 10 C1 7 C1 9 7 30； P(X2) C2 3 C2 10 C1 7 C1 8 7 120；P(X3) C3 3 C3 10 C1 7 C1 7 1 120 X 的分布列为 X 0 1 2 3 P 7 10 7 30 7 120 1 120 故 E(X)0 7 101 7 302 7 1203 1 1
28、20 3 8 【点拨】 有放回抽样可视作独立重复试验， 抽样时总体个数不发 生变化；无放回抽样时总体个数减少注意样本空间选取的不同对概 率计算的影响 (1)(2020山东邹城一中月考)“总把新桃换旧符”(王安石)、“灯前小草写桃符”(陆 游)，春节是中华民族的传统节日，在宋代人们用写“桃符”的方式来祈福避祸，而现代人们通过 贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿某商家在春节前开展商品促销活 动，顾客凡购物金额满 50 元，则可以从“福”字、春联和灯笼这三类礼品中任意免费领取一件， 若有 4 名顾客都领取一件礼品，则他们中有且仅有 2 人领取的礼品种类相同的概率是 ( ) A5
29、9 B 4 9 C 7 16 D 9 16 解：由题意知，基本事件总数为 n3481， 有且仅有 2 人领取的礼品种类相同包含的基本事件个数 mC2 4A 3 336，则所求 概率 Pm n 36 81 4 9故选 B (2)一个盒子中装有 5 张卡片，分别写着数字 1，2，3，4，5，现从盒子中随机 抽取卡片 ()从盒中依次抽取两次卡片，每次抽取一张，取出的卡片不放回，求两次取 到的卡片的数字既不全是奇数，也不全是偶数的概率； ()若从盒子中有放回的抽取 3 次卡片，每次抽取一张，求恰有两次取到卡片 的数字为偶数的概率； ()从盒子中依次抽取卡片，每次抽取一张，取出的卡片不放回，当取到记有
30、奇数的卡片即停止抽取，否则继续抽取卡片，求抽取次数 X 的分布列和期望 解：()因为 1，3，5 是奇数，2，4 是偶数， 设事件 A 为“两次取到的卡片的数字既不全是奇数，也不全是偶数” ， 则 P(A)C 1 3C 1 2 C2 5 3 5 另解：P(A)1P(A)1C 2 3C 2 2 C2 5 3 5 ()设事件 B 为“有放回地抽取 3 次卡片，每次抽取一张，恰有两次取到的卡片上数字 为偶数”，由已知，每次取到的卡片上数字为偶数的概率为2 5， 则 P(B)C2 3 2 5 2 12 5 36 125 ()依题意，X 的可能取值为 1，2，3 P(X1)3 5，P(X2) 23 54
31、 3 10， P(X3)213 543 1 10， 所以 X 的分布列为 X 1 2 3 P 3 5 3 10 1 10 E(X)13 52 3 103 1 10 3 2 命题角度 3 间接计算 (2020湖南邵阳市邵东十中模拟)现有甲、乙、丙、丁、戊 5 种在线 教学软件，若某学校要从中随机选取 3 种作为教师“停课不停学”的教学工 具，则其中甲、乙、丙至多有 2 种被选取的概率为 ( ) A2 3 B 2 5 C3 5 D 9 10 解： 记事件 A： “甲、 乙、 丙至多有 2 种被选取”的对立事件为A： “甲、 乙、 丙都被选取”， 依题意所有基本事件有 C3 510 个，其中事件A所
32、包含的基本事件数为 1，所以 P(A) 1 10，所求 事件 A 的概率为 P(A)1P(A)1 1 10 9 10故选 D 【点拨】 间接计算是计算概率十分常用的方式，是“正难则反”策略的体现， 对于含“至多”“至少”等词句的概率问题，一般情况下应首先考虑利用这一策 略高考概率大题对间接计算的考查也比较常见，尤其是计算含个别比较复杂概率 的分布列或期望问题 4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都 有同学参加公益活动的概率为( ) A1 8 B 3 8 C5 8 D 7 8 解：4 名同学各自在周六、周日两天中任选一天参加公益活动的情况有 24 16(种)，其中仅在周六或周日参加公益活动的情况各有 1 种，所以所求概率 为 111 16 7 8故选 D
