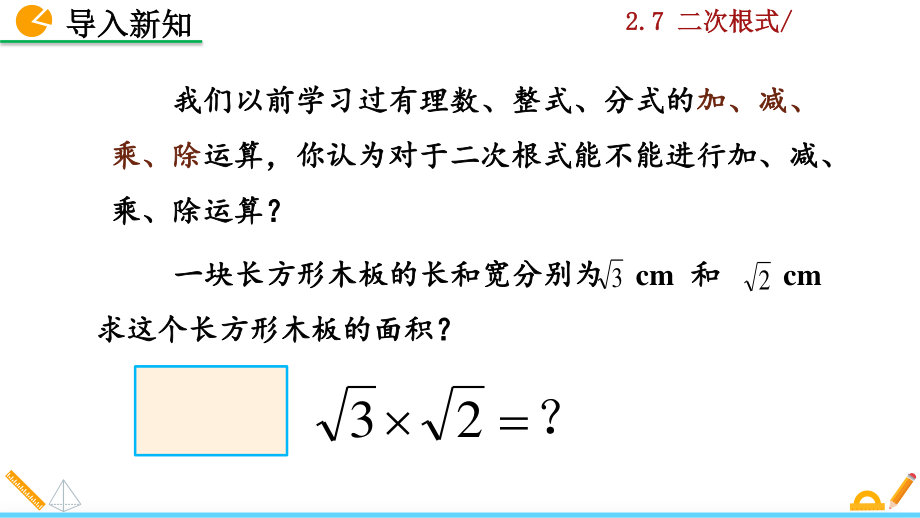
1、2.7 2.7 二次根式二次根式/ / 2.7 2.7 二次根式二次根式（第第2 2课时）课时） 北师北师大大版版 数学数学 八年级八年级 上册上册 2.7 2.7 二次根式二次根式/ / 我们以前学习我们以前学习过有理数过有理数、整式、分式的、整式、分式的加、减、加、减、 乘、除乘、除运算，你认为对于二次根式能不能进行加、减、运算，你认为对于二次根式能不能进行加、减、 乘、除运算？乘、除运算？ 2 3 一块一块长方形木板的长和宽分别为长方形木板的长和宽分别为 cm 和和 cm 求这个长方形木板的面积？求这个长方形木板的面积？ ？ 23 导入新知导入新知 2.7 2.7 二次根式二次根式/ /
2、 1. 探索二次根式乘法法则和除法法则探索二次根式乘法法则和除法法则. 2. 会运用二次根式的会运用二次根式的乘法法则乘法法则和和除法法则除法法则进行进行 简单运算简单运算. 素养目标素养目标 3. 用类比的方法，引入实数的用类比的方法，引入实数的运算法则、运算律运算法则、运算律， 并能用这些法则，运算律在并能用这些法则，运算律在实数范围实数范围内正确计算内正确计算. 2.7 2.7 二次根式二次根式/ / (1) _=_; =_; 49= 计算下列各式计算下列各式: : 1625 25 36 49 (2) _=_; (3) _=_; 2536= =_; =_. 1625 2 3 6 366
3、4 5 20 40020 5 6 30 90030 观察两者有什么关系？观察两者有什么关系？ 探究新知探究新知 知识点 1 二次根式的乘法二次根式的乘法 2.7 2.7 二次根式二次根式/ / 观察三组式子的结果，我们得到下面三个等式：观察三组式子的结果，我们得到下面三个等式： 你你发现了什么规律？你能用字母表示你所发现的规律吗？发现了什么规律？你能用字母表示你所发现的规律吗？ 猜测猜测 探究新知探究新知 这个式子与我们上节课学过的积的算数平方根的这个式子与我们上节课学过的积的算数平方根的 公式有什么关系？公式有什么关系？ 49= 49 ； 1625= 1625； 2536= 25 36. (
4、 (1) ) ( (2) ) ( (3) ) 2.7 2.7 二次根式二次根式/ / 一般地，对于二次根式的乘法是一般地，对于二次根式的乘法是 语言表述：语言表述： 算术平方根的算术平方根的积积等于各个被开方数等于各个被开方数积的算术平方根积的算术平方根. . 二次根式的乘法法二次根式的乘法法则是则是: : 二次根式相乘，二次根式相乘，_不变，不变，_相乘相乘. . 根指数根指数 被开方数被开方数 注意注意：a,b都必须是非负数都必须是非负数. . 在本章中， 如果没有特别 说明，所有的 字母都表示正 数 探究新知探究新知 0,0 .aba b ab 2.7 2.7 二次根式二次根式/ / 例
5、例1 计算计算: : 解解: : 探究新知探究新知 素养考点素养考点 1 简单的二次根式的乘法运算简单的二次根式的乘法运算 （1） ; （2） . 53 27 3 1 ( (1) ;) ; 3155 ( (2) .) . 1 27 3 1 2793 3 2.7 2.7 二次根式二次根式/ / 想一想想一想 下边下边的式子如何运算？的式子如何运算？ 解解: : ( 23)52356530 0,0,0)abka bkabk （ 235 探究新知探究新知 总结：总结：只需其中两个结合就可实现转化进行计算，说明二只需其中两个结合就可实现转化进行计算，说明二 次根式乘法法则同样适合三个及三个以上的二次根
6、式相乘次根式乘法法则同样适合三个及三个以上的二次根式相乘 （ ） 可先用乘法结合律，可先用乘法结合律， 再运用二次根式的乘再运用二次根式的乘 法法则法法则 2.7 2.7 二次根式二次根式/ / A. B. C. D. 1.计算计算 的结果是的结果是 ( ( ) ) A. B.4 C. D.2 106 C 2.下面计算结果正确的是下面计算结果正确的是( ( ) ) B 3.计算计算： _. 20 巩固练习巩固练习 2 1 12 11381025 12)2(61427 8105 变式训练变式训练 2.7 2.7 二次根式二次根式/ / 思考思考 你你还记得单项式乘单项式法则吗？还记得单项式乘单项
7、式法则吗？ 试回顾如何计算试回顾如何计算4a2 5a4= . 20a6 探究新知探究新知 2.7 2.7 二次根式二次根式/ / 例例2 计算计算: : 解解: : 0,0m a n bmnab ab 探究新知探究新知 素养考点素养考点 2 因数不是因数不是1 1二次根式的乘法运算二次根式的乘法运算 总结：总结：当二次根式根号外的因数不为当二次根式根号外的因数不为1 1时，可类比单项式时，可类比单项式 乘乘单项式单项式的法则计算，即的法则计算，即 （1） ; （2） . 7352）（3 2 1 -274 ( (1) ;) ; 2 32 57375536（）（） 可类可类比前比前 面面的的计计算
8、算 哦！哦！ ( (2) .) . 1 4-273 2 1 4 27-3 =-2 9=-18 2 （） （）（） 2.7 2.7 二次根式二次根式/ / 探究新知探究新知 归纳总结归纳总结 二次根式的乘法法则的推广：二次根式的乘法法则的推广： 多多个二次根式相乘时此法则也适用，即个二次根式相乘时此法则也适用，即 当当二次根号外有因数二次根号外有因数( (式式) )时，可以类比单项式乘单时，可以类比单项式乘单 项式的法则计算，即根号外的因数项式的法则计算，即根号外的因数( (式式) )的积作为根号外的积作为根号外 的因数的因数( (式式) )，被开方数的积作为被开方数，即，被开方数的积作为被开方
9、数，即 0,0m a n bmnab ab 0,0,00abcnabcn abcn 2.7 2.7 二次根式二次根式/ / 计算计算： 巩固练习巩固练习 解：解： 271245)( 20 43 3 9 2 20 (23 3) =2018=360 274125 ( (1) ) ; ( (2) .) . 61510 10156 2 3 3 5 52 2 (23 5) 30302 10156 ( (2) ) ( (1) ) 274125 变式训练变式训练 2.7 2.7 二次根式二次根式/ / ( (1) ) _=_; = _; 4 9 计算下列各式计算下列各式: : 16 25 36 49 4 9
10、 ( (2) ) _=_; ( (3) ) _=_; 36 49 = _; = _. 16 25 2 3 4 5 6 7 观察两者有什么关系？观察两者有什么关系？ 2 3 4 5 6 7 2 3 4 5 6 7 探究新知探究新知 知识点 2 二次根式的除法二次根式的除法 2.7 2.7 二次根式二次根式/ / 观察三组式子的结果，我们得到下面三个等式：观察三组式子的结果，我们得到下面三个等式： 44 = 99 ； 1616 2525 =； 3636 . 4949 ( (1) ) ( (2) ) ( (3) ) 猜想猜想 通过上述二次根式除法运算结果，联想到二次通过上述二次根式除法运算结果，联想
11、到二次 根式乘法运算法则，你能说出二次根式根式乘法运算法则，你能说出二次根式 的结果吗？的结果吗？ aa bb 特殊特殊 一般一般 a b 探究新知探究新知 2.7 2.7 二次根式二次根式/ / 在前面发现的规律在前面发现的规律 中，中，a,b的取值范围有没有限的取值范围有没有限 制呢？制呢？ aa bb a,b同号同号 就可以啦就可以啦 探究新知探究新知 你们都错啦，你们都错啦，a0， b0,b=0时等式两时等式两 边的二次根式就没边的二次根式就没 有意义啦有意义啦 不对，同乘法法不对，同乘法法 则一样，则一样，a,b都为都为 非负数非负数. 2.7 2.7 二次根式二次根式/ / 二次根
12、式的除法法则二次根式的除法法则: : (0,0). aa ab bb 文字叙述文字叙述: : 算术平方根的算术平方根的商商等于被开方数等于被开方数商的算术平方根商的算术平方根. . 当二次根式根号外的因数当二次根式根号外的因数( (式式) )不为不为1时，可类比单项式除时，可类比单项式除 以单项式法则，易得以单项式法则，易得 (0,0,0). m ama abn nbn b 探究新知探究新知 2.7 2.7 二次根式二次根式/ / 计算：计算： 解：解： 探究新知探究新知 素养考点素养考点 1 利用二次根式的除法进行计算利用二次根式的除法进行计算 3 2 6（1） （2） 2 36 ( (3)
13、 ) 5 2 3 2 6（1） 2 6 3 4=2 6 3 2 2 36 9=3 2 5 ( (2) ) 2 36 （3） 5 2 55 52 5 10 例例 在二次根式的运算中，在二次根式的运算中， 最后结果一般要求：最后结果一般要求： ( (1) )分母中不含有二分母中不含有二 次根式次根式. . ( (2) ) 最后结果中的二最后结果中的二 次根式要求写成最简次根式要求写成最简 的二次根式的形式的二次根式的形式. . 2.7 2.7 二次根式二次根式/ / 3232 2 2 计算计算： 解：解： 17 4 510 21 10 57 6. 巩固练习巩固练习 （1） ； （2） ； 10 7
14、 5 1 4 （3） . 32 2 32 164 2 （1） ; 5050 5 1010 （2） ; 5050 1010 （3） 10 7 5 1 4 变式训练变式训练 2.7 2.7 二次根式二次根式/ / （2）x2+2x2+4y= ; 1. .（1）3x2+2x2= ; 2. .类比合并同类项的方法，想想如何计算：类比合并同类项的方法，想想如何计算： 解：解： 答答：不能不能，因为它们都是最简二次根式，被开方数，因为它们都是最简二次根式，被开方数 不相同，所以不能合并不相同，所以不能合并. . 5x2 3x2+4y 知识点 3 二次根式的加减计算二次根式的加减计算 探究新知探究新知 45
15、-80 45-804 5-3 55 3. . 能不能再进行计算能不能再进行计算? ?为什么为什么? ? 53 2.7 2.7 二次根式二次根式/ / 解：解：( (1) )原式原式= = 计算计算: : ( (2) )原式原式= ( (3) )原式原式= ( (4) )原式原式= = 例例1 （1） 3223（2） 5-312 （3） 2 15 （4） 3-13313 （5） 3 3 1 -12 （6） 2 188 探究新知探究新知 2 2 13-3 =13-9=4 52 511525 526 12 3-55-36=6-5=1 3 22 3 66 素养考点素养考点 1 二次根式的加减乘除计算二
16、次根式的加减乘除计算 2.7 2.7 二次根式二次根式/ / 解：解：( (5) )原式原式= = ( (6) )原式原式= = （5） 3 3 1 -12 （6） 2 188 818 22 94 =2+3=5 1 123-3 3 1-36=6-1=5 探究新知探究新知 2.7 2.7 二次根式二次根式/ / 下列计算正确的是下列计算正确的是（ ） A. B. C. D. B 巩固练习巩固练习 133-34 532 3327 5205554 变式训练变式训练 2.7 2.7 二次根式二次根式/ / 知识点 计算：计算： . 6)3 3 4 )(3( ; 5 1 5)2( ; 348) 1 (
17、解解: : （1）原式原式 （2）原式原式 5 5- 25 5 5 -55 5 4 （3）原式原式 4 63 6 3 188232225 16 33331633435 例例2 探究新知探究新知 素养考点素养考点 2 二次根式的四则运算二次根式的四则运算 2.7 2.7 二次根式二次根式/ / 完成下列计算完成下列计算. . 19 502;6714. 67 (1) (2) ;(3)（） 解：解： （1）原式原式= = 25 22222522526 （2）原式原式= = 1 6 6 6 6 36 6 6 6 6 6 6 6 7 （3）原式原式= = 9 147 14 7 24929 2723210
18、 巩固练习巩固练习 变式训练变式训练 2.7 2.7 二次根式二次根式/ / 二次根式的加减法法则 一般一般地，二次根式加减时，可以先将二次根地，二次根式加减时，可以先将二次根 式化成最简二次根式，再将被开方数相同的二次根式化成最简二次根式，再将被开方数相同的二次根 式进行合并式进行合并. . 1. .加减法的运算步骤：“一化简二判断三合并”加减法的运算步骤：“一化简二判断三合并”. . 2. .合并的前提条件：只有被开方数相同的合并的前提条件：只有被开方数相同的 最简二次根式才能进行合并最简二次根式才能进行合并. . 探究新知探究新知 小结小结 提示提示 2.7 2.7 二次根式二次根式/
19、/ 818 2 2 3 22 32 5 2+=+=+=+=+=+=（） 化为最简化为最简 二次根式二次根式 用分配用分配 律合并律合并 整式整式 加减加减 二次根二次根 式性质式性质 分配律分配律 整式加整式加 减法则减法则 依据依据：二次根式的性质、分配律和整式加减法则：二次根式的性质、分配律和整式加减法则. . 基本思想基本思想：把二次根式加减问题转化为整式加减问题：把二次根式加减问题转化为整式加减问题 探究新知探究新知 2.7 2.7 二次根式二次根式/ / 1. （ ） A B4 C D 82 241022 连接中考连接中考 2. 一一个长方形的长和宽分别为个长方形的长和宽分别为 和和
20、 ，则这个长方，则这个长方 形的面积为形的面积为_ 102 2 4 5 B 2.7 2.7 二次根式二次根式/ / 1.化简化简 的结果是（的结果是（ ） A9 B3 C D 182 3 22 3 A. B. C. D. B 2.下面计算结果正确的是下面计算结果正确的是 ( ( ) ) 4 52 58 55 34 220 5 4 33 27 55 34 220 6 D 课堂检测课堂检测 基 础 巩 固 题基 础 巩 固 题 2.7 2.7 二次根式二次根式/ / 3. 计算：计算： 课堂检测课堂检测 基 础 巩 固 题基 础 巩 固 题 （4） =_ 3 903 5 5 （5） =_ （6）
21、=_ 12 -2 3 -1 15+ 205（）3+2 （1） =_ 153 （3） =_ 223 （2） =_ 1263 5 2 6 6 2 2.7 2.7 二次根式二次根式/ / 4. 计算计算： 解：解： 课堂检测课堂检测 基 础 巩 固 题基 础 巩 固 题 （1） （2） 1 18- 2 181 + 32-50 35 1 1= 9 2- 2 （）原式 2 =3 2- 2 5 2 = 2 9 21 2=+ 16 2-25 2 35 （ ）原式 3 21 =+4 2-5 2 35 = 2+4 2- 2=4 2 2.7 2.7 二次根式二次根式/ / 5.计算计算： 2 53 21 30 7
22、 1 3-318 4 2 3 36 4 3 36 4 9 6. 4 课堂检测课堂检测 （1） 21532（2） ）（ 4 18 -33 解：解： （1） 21532（2） ）（ 4 18 -33 基 础 巩 固 题基 础 巩 固 题 2 10 37 2.7 2.7 二次根式二次根式/ / 1.下面是意大利艺术家列奥纳多下面是意大利艺术家列奥纳多达达芬奇所创作世界名画，若芬奇所创作世界名画，若 长为长为 ，宽为，宽为 ，求出它的面积，求出它的面积. . 248 解：解：它的面积为它的面积为 能 力 提 升 题能 力 提 升 题 82424 838238 课堂检测课堂检测 2.7 2.7 二次根式
23、二次根式/ / 2.设长方形的面积为设长方形的面积为S，相邻两边分别为，相邻两边分别为a,b. . ( (1) )已知已知 , , ，求，求S； 8a 12b 解：解： S = ab = 812 （2）已知）已知 , , ，求，求S. . 2 50a 323b 2 50 3 32 课堂检测课堂检测 能 力 提 升 题能 力 提 升 题 8 12= （1） S = ab = （2） =240 2 42 3 = 4 6= 650 32= 2 640= 2.7 2.7 二次根式二次根式/ / 已知已知 试着用试着用a, b表示表示 . 7, 70,ab 4.9 解解： 课堂检测课堂检测 拓 广 探
24、索 题拓 广 探 索 题 4.910010 4.9, 又又因为因为 因为因为 10 4.9,ab 所以所以 所以所以 1 4.9. 10 ab 2.7 2.7 二次根式二次根式/ / 二次根式二次根式 的运算的运算 乘法法则乘法法则 加减法则加减法则 乘法公式乘法公式 课堂小结课堂小结 除法法则除法法则 (a+b)(a-b)=a2-b2 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 (x+a)(x+b)=x2+(a+b)x+ab 加减法的运算步骤：“一化简二判断加减法的运算步骤：“一化简二判断 三合并”三合并”. . (0,0). aa ab bb 0,0 .aba b ab 2.7 2.7 二次根式二次根式/ / 课后作业课后作业 作业 内容 教材作业 从课后习题中选取从课后习题中选取 自主安排 配套练习册练习配套练习册练习
