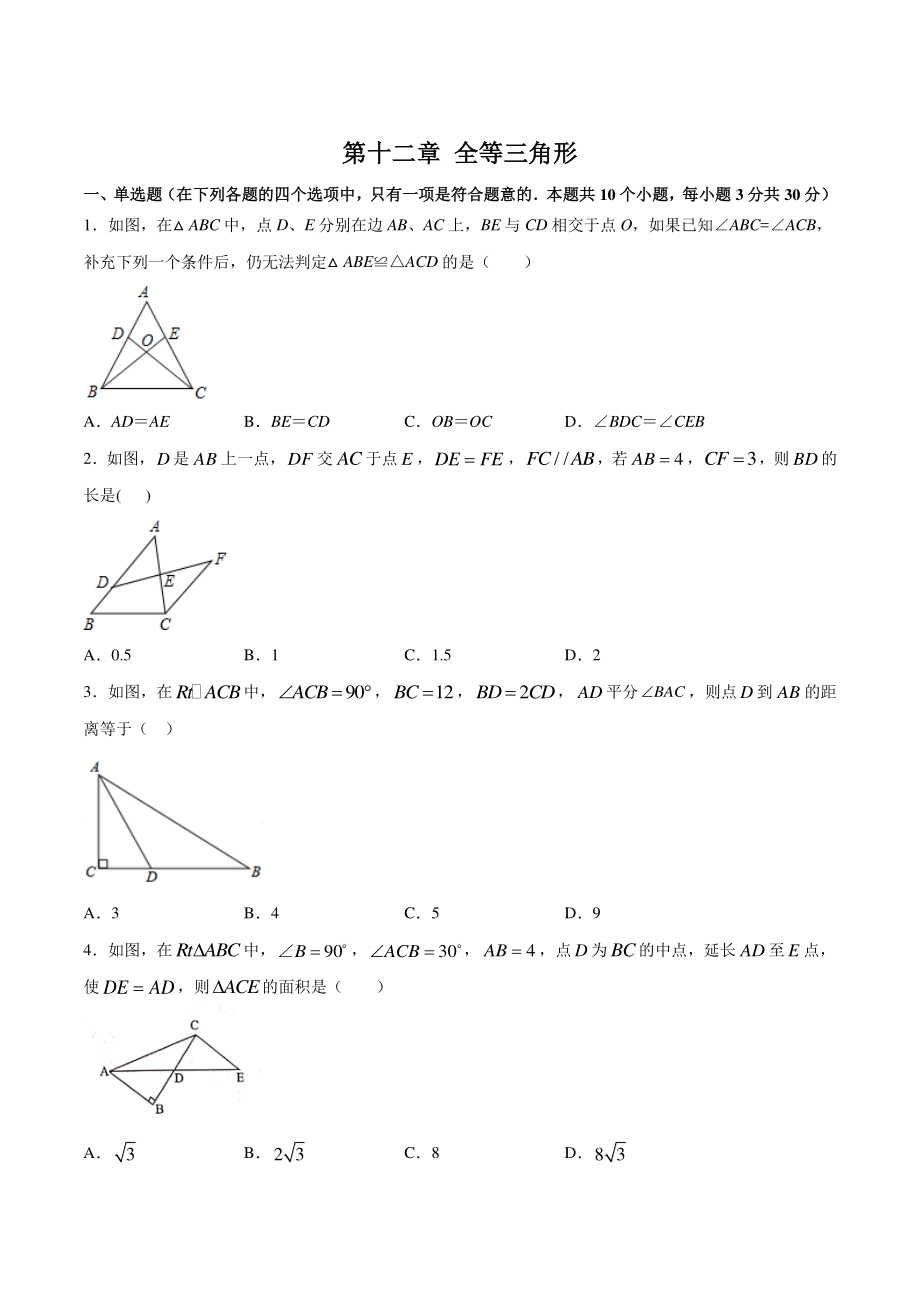
1、第十二章第十二章 全等三角形全等三角形 一、单选题（在下列各题的四个选项中，只有一项是符合题意的本题共一、单选题（在下列各题的四个选项中，只有一项是符合题意的本题共 10 个小题，每小题个小题，每小题 3 分共分共 30 分）分） 1如图，在 ABC 中，点 D、E 分别在边 AB、AC 上，BE 与 CD 相交于点 O，如果已知ABC=ACB， 补充下列一个条件后，仍无法判定 ABEACD 的是（ ） AADAE BBECD COBOC DBDCCEB 2如图，D是AB上一点，DF交AC于点E，DEFE ，/FCAB，若4AB ，3CF ，则BD的 长是( ) A0.5 B1 C1.5 D2
2、 3如图，在Rt ACB中，90ACB，12BC ，2BDCD，AD平分BAC，则点D到AB的距 离等于（ ） A3 B4 C5 D9 4如图，在Rt ABC中，90B ，30ACB ，4AB ，点D为BC的中点，延长AD至E点， 使DEAD，则ACE的面积是（ ） A3 B2 3 C8 D8 3 5 已知 ABCDEF， 若 ABC 的周长为 30cm， AB8cm， BC12cm， 则 DE、 DF 的长度分别是 （ ） A8cm 和 9cm B8cm 和 10cm C10cm 和 12cm D8cm 和 12cm 6如图，用直尺和圆规作一个角的平分线，该作法的依据是 ASSS BSAS
3、CASA DAAS 7如图， ABD 和 ACE 分别是等边三角形，ABAC，下列结论中正确有（ ）个. DC=BE，BOD=60 ，BDO=CEO，AO 平分DOE，AO 平分BAC A2 B3 C4 D5 8下列命题中，是假命题的是（ ） A两条直角边对应相等的两个直角三角形全等 B两个锐角对应相等的两个直角三角形全等 C斜边和一条直角边对应相等的两个直角三角形全等 D斜边和一个锐角对应相等的两个直角三角形全等 9如图，在 Rt ABC 中，C90 ，D 是 AB 的中点，E 在边 AC 上，若 D 与 C 关于 BE 成轴对称，则下 列结论：A30 ；ABE 是等腰三角形；点 B 到CE
4、D 的两边距离相等其中正确的有（ ） A0 个 B1 个 C2 个 D3 个 10如图，任意画一个60BAC的ABC，再分别作ABC的两条角平分线BE和CD，BE和CD相 交于点P，连接AP，有以下结论：120BPC；: ABPACP SSAB AC ；PD PE； ADAE；BD CEBC其中正确的结论为（ ） A1 个 B2 个 C3 个 D4 个 二、填空题（本题共二、填空题（本题共 8 个小题，每小题个小题，每小题 3 分共分共 24 分）分） 11如图，已知ABCBAD，判定ABC BAD，需添加的条件是_ （只需填一个条 件） 12 如图，ABC中，ADBC于 D， 要使ABDAC
5、D ， 若根据“HL”判定， 还需要加条件_ 13如图，已知1=2，AC=AD，请增加一个条件，使 ABCAED，你添加的条件是_（只 要写出一个答案） 14如图, /AD BC，、BGAG分别平分ABC与BAD，GHAB，4HG，则AD与BC之间的 距离是_ 15如图，在 Rt ABC 中，C90 ，A30 ，AC3，则斜边 AB_ 16如图，已知 ABC 和 DCE 均是等边三角形，点 B，C，E 在同一条直线上，AE 与 CD 交于点 G，AC 与 BD 交于点 F，连接 FG，则下列结论： AE=BD；AG =BF；FGBE；CF=CG.其中正确的结论 为_. 17如图所示的网格是正方
6、形网格，图形的各个顶点均为格点，则1+2_ 18如图，4cmAB，3cmACBD，CABDBA ，点P在线段AB上以1cm/s的速度由点A 向点B运动，同时，点Q在线段BD上由点B向点D运动，设运动时间为 s t ，则当ACP与BPQV全 等时，点Q的运动速度为_cm/s 三、解答题（本大题共三、解答题（本大题共 7 小题，小题，19、20 小题每小题小题每小题 6 分，分，21、22 每小题每小题 8 分，分，23、24 每小题每小题 9 分，分，25、26 每小题每小题 10 分，共分，共 66 分分.解答应写出文字说明、证明过程或演算步骤解答应写出文字说明、证明过程或演算步骤.） 19已
7、知：如图，点 A，D，B，E 在同一条直线上，ABC=EDF，AD=BE，BC=DF. 求证：AC=EF. 20如图，E为BC上一点，AC BD，AC BE，ABDCED .求证：ABED. 21 如图所示，D是BC上一点，ABAD，BCDE，ACAE ，AC与DE交于点F 求证：CE 22如图，已知AOB，求作射线OC，使 AO CBO C（要求：尺规作图，保留作图痕迹，不写作法） ， 并说明其中的道理 23如图，ABC中， 3AB ，4AC ，AD为中线，求中线AD的取值范围 24如图，ABC中，D是边BC的中点，过点C作 / /,CEAB交AD的延长线于点E求证:D是AE的 中点 证明:
8、/ /CEAB(已知)， B_ (两直线平行，内错角相等)， DQ是边BC的中点， BD(_ ） ，(_ ） ， 在ABD和ECD中， ADBEDC BDCD BBCE ， ABDECD( ) ， AD (全等三角形的对应边相等)， D是AE的中点 25在ABC中， 90 ,ACBACBC ，直线MN经过点 C，且ADMN于 D，BEMN于 E， （1）当直线MN绕点 C 旋转到图 1 的位置时，显然有：DEADBE（不必证明） ； （2）当直线MN绕点 C 旋转到图 2 的位置时，求证：DEADBE； （3）当直线MNMN 绕点 C 旋转到图 3 的位置时，试问DE、AD、BE具有怎样的等量
9、关系？请直接写 出这个等量关系 26如图 1，图 2，图 3，在ABC中，分别以AB AC，为边，向ABC外作正三角形，正四边形，正五 边形，BECD，相交于点O （正多边形的各边相等，各个内角也相等） 如图 1，求证： ABEADC； 探究：如图 1，BOD= o； 如图 2，BOD= o； 如图 3，BOD= o 第十二章第十二章 全等三角形全等三角形 一、单选题（在下列各题的四个选项中，只有一项是符合题意的本题共一、单选题（在下列各题的四个选项中，只有一项是符合题意的本题共 10 个小题，每小题个小题，每小题 3 分共分共 30 分）分） 1如图，在 ABC 中，点 D、E 分别在边 A
10、B、AC 上，BE 与 CD 相交于点 O，如果已知ABC=ACB， 补充下列一个条件后，仍无法判定 ABEACD 的是（ ） AADAE BBECD COBOC DBDCCEB 【答案】B 【分析】 根据题目中的条件和各个选项中的条件，利用全等三角形的判定方法，可以得到哪个选项中的条件，不能 判定 ABEACD，从而可以解答本题 【详解】 解：ABC=ACB， AB=AC， BAE=CAD， 补充条件 AD=AE 时， ABEACD（SAS） ，故选项 A 不符合题意； 补充条件 BE=CD，无法判断 ABEACD，故选项 B 符合题意； 补充条件 OB=OC 时，则OBC=OCB，故ABE
11、=ACD，则 ABEACD（ASA） ，故选项 C 不符合 题意； 补充条件BDC=CEB 时，则AEB=ADC，则 ABEACD（AAS） ，故选项 D 不符合题意； 故选：B 【点睛】 本题考查全等三角形的判定，解答本题的关键是明确全等三角形的判定方法，利用数形结合的思想解答 2如图，D是AB上一点，DF交AC于点E，DEFE ，/FCAB，若4AB ，3CF ，则BD的 长是( ) A0.5 B1 C1.5 D2 【答案】B 【分析】 根据平行线的性质，得出AFCE ，ADEF ，根据全等三角形的判定，得出ADECFE， 根据全等三角形的性质，得出ADCF，根据4AB ，3CF ，即可求
12、线段DB的长 【详解】 /CFAB， AFCE ，ADEF ， 在ADE和FCE中 AFCE ADEF DEFE ， ADECFE AAS ， 3ADCF， 4AB ， 4 3 1DBABAD . 故选 B 【点睛】 本题考查了全等三角形的性质和判定，平行线的性质的应用，能判定ADEFCE是解此题的关键 3如图，在Rt ACB中，90ACB，12BC ，2BDCD，AD平分BAC，则点D到AB的距 离等于（ ） A3 B4 C5 D9 【答案】B 【分析】 根据角平分线的性质“角的平分线上的点到角的两边的距离相等”， 可得点 D 到 AB 的距离=点 D 到 AC 的距 离=CD 【详解】 解
13、：BC=12，BD=2CD， CD=4， 由角平分线的性质，得点 D 到 AB 的距离等于 CD=4 故选：B 【点睛】 本题主要考查平分线的性质，由已知能够注意到 D 到 AB 的距离即为 CD 长是解决的关键 4如图，在Rt ABC中，90B ，30ACB ，4AB ，点D为BC的中点，延长AD至E点， 使DEAD，则ACE的面积是（ ） A3 B2 3 C8 D8 3 【答案】D 【分析】 由直角三角形的性质可求 AC=8，BC= 3AB=43，可求 ABC 的面积，由“SAS”可证 ADBEDC， 可得 S ADB=S EDC，即可求解 【详解】 解：B=90 ，ACB=30 ，AB=
14、4， AC=8，BC= 3AB=43， S ABC= 1 2 AB BC=8 3， 点 D 为 BC 的中点， CD=BD， 在 ADB 和 EDC 中， ADDE ADBCDE DBDC ， ADBEDC（SAS） ， S ADB=S EDC， S ABC=S ACE=8 3， 故选：D 【点睛】 本题考查了全等三角形的判定和性质，直角三角形的性质，证明 ADBEDC 是本题的关键 5 已知 ABCDEF， 若 ABC 的周长为 30cm， AB8cm， BC12cm， 则 DE、 DF 的长度分别是 （ ） A8cm 和 9cm B8cm 和 10cm C10cm 和 12cm D8cm
15、和 12cm 【答案】B 【分析】 根据三角形的周长为 30cm，可计算出 AC 的长，再利用全等三角形的性质可得 DE、DF 的长度 【详解】 AB8cm，BC12cm， AC3081210（cm） ， ABCDEF， DEAB8cm，DFAC10cm， 故选：B 【点睛】 此题主要考查了全等三角形的性质，关键是掌握全等三角形的对应边相等 6如图，用直尺和圆规作一个角的平分线，该作法的依据是 ASSS BSAS CASA DAAS 【答案】A 【分析】 根据题意易知：OB=OA，BC=AC，OC=OC，因此符合 SSS 的条件 【详解】 解：如图 解：连接 BC，AC， 由作图知：在 OAC
16、 和 OBC 中， OAOB COCO ACBC OACOBC（SSS） ， 故选 A 【点睛】 本题考查的是全等三角形的判定，要清楚作图时作出的线段 OB 与 OA、BC 与 AC 是相等的 7如图， ABD 和 ACE 分别是等边三角形，ABAC，下列结论中正确有（ ）个. DC=BE，BOD=60 ，BDO=CEO，AO 平分DOE，AO 平分BAC A2 B3 C4 D5 【答案】B 【分析】 根据等边三角形的性质推出 AD=AB，AE=AC，ADB=ABD=60 ，DAB=EAC=60 ，求出 DAC=BAE，根据 SAS 证 DACBAE，推出 BE=DC，ADC=ABE，根据三角
17、形的内角和定理 求出BOD=180 -ODB-DBA-ABE=60 ，根据等边三角形性质得出ADB=AEC=60 ，但 ADCAEB，过点 A 作 AFDC，AHBE，根据三角形全等得 AF=AH，则点 A 到角两边距离相等， 故点 A 在角角平分线上，根据以上推出的结论即可得出答案 【详解】 ABD 与 AEC 都是等边三角形， AD=AB,AE=AC,ADB=ABD=60 ,DAB=EAC=60 ， DAB+BAC=EAC+BAC， DAC=BAE， 在 DAC 和 BAE 中 ADAB DACBAE ACAE ， DACBAE(SAS), BE=DC，ADC=ABE， BOD=180OD
18、BDBAABE=180ODB60ADC=120(ODB+ADC)=12060=60 BOD=60 ， 正确；正确； ABD 与 AEC 都是等边三角形， ADB=AEC=60 ，但根据已知不能推出ADC=AEB， 说BDO=CEO 错误，错误； 过点 A 作 AFDC，AHBE，分别交 DC 与 BE 与点 F、H. DACBAE， AF=AH， 则点 A 在DOE 的角平分线上， OA 平分DOE，正确； 根据已知条件不能证明 OA 平分BAC， 错误. 故答案选：B. 【点睛】 本题考查了等边三角形的性质以及全等三角形的判定与性质，解题的关键是熟练的掌握等边三角形的性质 以及全等三角形的判
19、定与性质. 8下列命题中，是假命题的是（ ） A两条直角边对应相等的两个直角三角形全等 B两个锐角对应相等的两个直角三角形全等 C斜边和一条直角边对应相等的两个直角三角形全等 D斜边和一个锐角对应相等的两个直角三角形全等 【答案】B 【分析】 根据直角三角形的判定定理可直接进行排除选项 【详解】 A、两条直角边对应相等的两个直角三角形全等，符合“SAS”判定方法，故是真命题； B、两个锐角对应相等的两个直角三角形不全等，因为没有对应边的相等，故是假命题； C、斜边和一条直角边对应相等的两个直角三角形全等，符合“HL”判定方法，故是真命题； D、斜边和一个锐角对应相等的两个直角三角形全等，符合“
20、ASA”或“AAS”的判定方法，故是真命题； 故选 B 【点睛】 本题主要考查直角三角形的判定定理，熟练掌握直角三角形的判定定理是解题的关键 9如图，在 Rt ABC 中，C90 ，D 是 AB 的中点，E 在边 AC 上，若 D 与 C 关于 BE 成轴对称，则下 列结论：A30 ；ABE 是等腰三角形；点 B 到CED 的两边距离相等其中正确的有（ ） A0 个 B1 个 C2 个 D3 个 【答案】D 【解析】 【分析】 根据题意需要证明 Rt BCERt BDE, Rt EDARt EDB，即可解答 【详解】 D 与 C 关于 BE 成轴对称 Rt BCERt BDE（SSS） BCE
21、BDE EDB=EDA=90 ，BD=BC 又D 是 AB 的中点 AD=DB Rt EDARt EDB(HL) A30 （直角三角形含 30 角，BC= 1 2 AB） ABE 是等腰三角形 点 B 到CED 的两边距离相等 故选 D 【点睛】 此题考查全等三角形的判定和直角三角形的性质，解题关键在于利用全等三角形的判定求解 10如图，任意画一个60BAC的ABC，再分别作ABC的两条角平分线BE和CD，BE和CD相 交于点P，连接AP，有以下结论：120BPC；: ABPACP SSAB AC ；PD PE； ADAE；BD CEBC其中正确的结论为（ ） A1 个 B2 个 C3 个 D
22、4 个 【答案】D 【分析】 在 BC 上取 BF=BD，通过 SAS 证 BDPBFP，ASA 证 CPFCPE，作 PGAB 于 G，PHAC 于 H 通过 AAS 证 DPGEPH 即可判断各结论 【详解】 解：ABC 的两条角平分线 BE 和 CD 交于 P，BAC=60 PBC+PCB= 1 2 (ABC+ACB) 1 180 2 BAC60 ， BPC=180 -60 =120 ，故正确； BPD=60 ， 在 BC 上取 BF=BD， BP 平分ABC， ABP=CBP， 在 BDP 和 BFP 中， BDBF DBPFBP BPBP ， BDPBFP（SAS） ， BPD=BP
23、F=60 ， BPC=120 ， FPC=EPC=60 ， CPFCPE（ASA） ， CE=CF， BC=BD+CE，故正确； 作 PGAB 于 G，PHAC 于 H， BAC=60 ， GPH=120 ， DPE=BPC=120 ， DPG=EPH， DPGEPH（AAS） PG=PH，PD=PE，故正确； AD-DG=AE+EH， AD-AE=2DG，故不正确； AP 是角平分线， P 到 AB、AC 的距离相等， S ABP：S ACP=AB：AC， 故正确 故选：D 【点睛】 本题主要考查了三角形全等的判定与性质，角平分线的性质，作出辅助线构造全等三角形是解题的关键 二、填空题（本题
24、共二、填空题（本题共 8 个小题，每小题个小题，每小题 3 分共分共 24 分）分） 11如图，已知ABCBAD，判定ABC BAD，需添加的条件是_ （只需填一个条 件） 【答案】ADCB 【解析】 若ADCB，ABCBAD，ABAB， 则ABC(SAS)BAD， 故答案为：AD=BC（答案不唯一）. 12 如图，ABC中，ADBC于 D， 要使ABDACD ， 若根据“HL”判定， 还需要加条件_ 【答案】AB=AC 【详解】 解： 还需添加条件 AB=AC ADBC 于 D， ADB=ADC=90 在 Rt ABD 和 Rt ACD 中， AB=AC， AD=AD，Rt ABDRt AC
25、D（HL） 故答案为 AB=AC 13如图，已知1=2，AC=AD，请增加一个条件，使 ABCAED，你添加的条件是_（只 要写出一个答案） 【答案】AE=AB（答案不唯一） 【分析】 添加条件 AB=AE，由等式的性质得到BAC=EAD，再利用 SAS 证明 BACEAD 【详解】 添加 AE=AB， 1=2， 1+EAB=2+EAB， BAC=EAD， 在 BCA 和 EDA 中， ACAD BACEAD ABAE ， BACEAD（SAS） 故答案为：AB=AE 【点睛】 考查了三角形全等的判定方法，解题关键是判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、 HL 14如
26、图, /AD BC，、BGAG分别平分ABC与BAD，GHAB，4HG，则AD与BC之间的 距离是_ 【答案】8 【分析】 过点 G 作 GFBC 于 F，交 AD 于 E，根据角平分线的性质得到 GF=GH=5，GE=GH=5，计算即可 【详解】 解：过点 G 作 GFBC 于 F，交 AD 于 E， ADBC，GFBC， GEAD， AG 是BAD 的平分线，GEAD，GHAB， GE=GH=4， BG 是ABC 的平分线，FGBC，GHAB， GF=GE=4， EF=GF+GE=8， 故答案为：8 【点睛】 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键
27、 15如图，在 Rt ABC 中，C90 ，A30 ，AC3，则斜边 AB_ 【答案】2 3 【解析】 C=90 ，A=30 ，AB=2BC，AB2=BC2+AC2 ,又AC=3，AB=23 . 16如图，已知 ABC 和 DCE 均是等边三角形，点 B，C，E 在同一条直线上，AE 与 CD 交于点 G，AC 与 BD 交于点 F，连接 FG，则下列结论： AE=BD；AG =BF；FGBE；CF=CG.其中正确的结论 为_. 【答案】 【分析】 首先由 SAS 判定 BCDACE，即可证得正确； 又由全等三角形的对应角相等， 得到CBD=CAE， 根据 ASA，证得 BCFACG，即可得到
28、正确，同理证得 CF=CG，则正确，可得FCE=60 ，可得 CFG 是等边三角形，则可得CFG=FCB，则 FGBE，可得正确 【详解】 解：ABC 和 DCE 均是等边三角形， BC=AC，CD=CE，ACB=ECD=60 ， ACB+ACD=ACD+ECD，ACD=60 ， BCDACE（SAS） ， AE=BD， （正确） CBD=CAE， BCA=ACG=60 ，AC=BC， BCFACG（ASA） ， AG=BF， （正确） CF=CG（正确） ，且ACD=60 CFG 是等边三角形， CFG=FCB=60 ， FGBE， （正确） 正确的有 【点睛】 本题的关键是熟练掌握等边三角
29、形的判定与性质，全等三角形的判定与性质，应用数形结合思想 17如图所示的网格是正方形网格，图形的各个顶点均为格点，则1+2_ 【答案】135 【分析】 直接利用网格证明 ABCCDE，得出对应角1=3，进而得出答案 【详解】 解：如图所示： 可知：AB=CD=3，BC=DE=1，B=D=90 ， ABCCDE（SAS） ， 1=3， 则1+2=2+3=135 故答案为：135 【点睛】 此题主要考查了全等三角形的判定和性质，正确借助网格分析是解题关键 18如图，4cmAB，3cmACBD，CABDBA ，点P在线段AB上以1cm/s的速度由点A 向点B运动，同时，点Q在线段BD上由点B向点D运
30、动，设运动时间为 s t ，则当ACP与BPQV全 等时，点Q的运动速度为_cm/s 【答案】1 或 3 2 【分析】 设点 Q 的运动速度是 x cm/s，有两种情况：AP=BP，AC=BQ，AP=BQ，AC=BP，列出方程，求出方程 的解即可 【详解】 解：设点 Q 的运动速度是 x cm/s， CAB=DBA， ACP 与 BPQ 全等，有两种情况： AP=BP，AC=BQ， 则 1 t=4-1 t， 解得：t=2， 则 3=2x， 解得：x= 3 2 ； AP=BQ，AC=BP， 则 1 t=tx，4-1 t=3， 解得：t=1，x=1， 综上所述，点Q的运动速度为 1 或 3 2 ；
31、 故答案为：1 或 3 2 【点睛】 本题考查了全等三角形的判定的应用，掌握方程的思想和分类讨论思想是解此题的关键 三、解答题（本大题共三、解答题（本大题共 7 小题，小题，19、20 小题每小题小题每小题 6 分，分，21、22 每小题每小题 8 分，分，23、24 每小题每小题 9 分，分，25、26 每小题每小题 10 分，共分，共 66 分分.解答应写出文字说明、证明过程或演算步骤解答应写出文字说明、证明过程或演算步骤.） 19已知：如图，点 A，D，B，E 在同一条直线上，ABC=EDF，AD=BE，BC=DF. 求证：AC=EF. 【答案】证明见解析 【分析】 结合图形可得 AD+
32、BD=BE+BD，得出 AB=ED，再利用全等三角形的判定定理即可证明 ABCEDF SAS（），从而得出结论 【详解】 解：ADBE ADBDBEBD ABDE 在ABC和EDF 中 A BDE A B CE DF B CDF ABCEDF SAS（） ACEF 【点睛】 本题考查的知识点是全等三角形的判定定理及其性质，熟记定理和性质是解题的关键 20如图，E为BC上一点，AC BD，AC BE，ABDCED .求证：ABED. 【答案】详见解析 【分析】 先由平行线的性质得ACBEBD，再由角的和与差得ABCEDB，根据AAS定理可得 ABCEDB，最后根据三角形全等的性质即可得. 【详解
33、】 /ACBD ACBEBD ,ABDCEDABDABCEBDCEDEBDEDB ABCEDB 在ABC与EDB中， ABCEDB ACBEBD ACBE ()ABCEDB AAS ABED. 【点睛】 本题考查了三角形全等的判定定理与性质，熟记判定定理与性质是解题关键. 21 如图所示，D是BC上一点，ABAD，BCDE，ACAE ，AC与DE交于点F 求证：CE 【答案】证明见解析 【分析】 利用“边边边”证明ABC和ADE全等，根据全等三角形对应角相等证明即可； 【详解】 证明：在ABC和ADE中， ABAD BCDE ACAE ， ()ABCADE SSS ， CE（全等三角形对应角相
34、等） ； 【点睛】 本题考查了全等三角形的判定与性质，熟练掌握三角形全等的判定方法是解题的关键 22如图，已知AOB，求作射线OC，使 AO CBO C（要求：尺规作图，保留作图痕迹，不写作法） ， 并说明其中的道理 【答案】见解析. 【解析】 【分析】 利用基本作图（作已知角的角平分线）作出 OC，同时得到 OC，然后根据“SSS“判断 ODPOEP 得到 DOP=EOP，再根据等角的补角相等得到AOC=BOC 【详解】 解：如图，射线OC或OC为所作 通过证明ODPOEP 得到DOPEOP ， 然后根据等角的补角相等得到AOCBOC 【点睛】 本题考查了作图-基本作图：熟练掌握基本作图（作
35、一条线段等于已知线段；作一个角等于已知角；作已知 线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线） 23如图，ABC中， 3AB ，4AC ，AD为中线，求中线AD的取值范围 【答案】 17 22 AD 【分析】 延长AD至点E，使DEAD，连接CE，证明ABDCDE，得到4ABEC，然后根据三角形三条 边的关系求解即可 【详解】 解：延长AD至点E，使DEAD，连接CE， AD是中线， BDCD， 在ABD和ECD中， ADDE ADBCDE BDCD ， ()ABDCDE SAS ， 4ABEC， 在ACE中，AC CEAEACCE， 43243AD ， 127AD ， 17
36、 22 AD 【点睛】 本题考查了三角形三条边的关系， 以及全等三角形的判定和性质， 掌握全等三角形的判定方法 （即 SSS、 SAS、 ASA、AAS 和 HL）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键 24如图，ABC中，D是边BC的中点，过点C作 / /,CEAB交AD的延长线于点E求证:D是AE的 中点 证明:/ /CEAB(已知)， B_ (两直线平行，内错角相等)， DQ是边BC的中点， BD(_ ） ，(_ ） ， 在ABD和ECD中， ADBEDC BDCD BBCE ， ABDECD( ) ， AD (全等三角形的对应边相等)， D是AE的中点
37、【答案】;BCE CD；线段中点的定义；;ASA ED 【分析】 利用中线类倍长的基本模型进行证明，结合平行线的性质进行论证 【详解】 证明:/ /CEAB(已知)， BBCE (两直线平行，内错角相等)， DQ是边BC的中点， BDCD(线段中点的定义)， 在ABD和ECD中， ADBEDC BDCD BBCE ABDECD ASA ， ADED(全等三角形的对应边相等)， D是AE的中点 【点睛】 本题考查了类倍长中线的模型，能够通过平行结合中点问题，推出三角形全等，是解决问题的关键 25在ABC中， 90 ,ACBACBC ，直线MN经过点 C，且ADMN于 D，BEMN于 E， （1）
38、当直线MN绕点 C 旋转到图 1 的位置时，显然有：DEADBE（不必证明） ； （2）当直线MN绕点 C 旋转到图 2 的位置时，求证：DEADBE； （3）当直线MNMN 绕点 C 旋转到图 3 的位置时，试问DE、AD、BE具有怎样的等量关系？请直接写 出这个等量关系 【答案】 （1）见解析； （2）见解析； （3）DE=BE-AD 【分析】 （1）由于 ABC 中，ACB=90 ，AC=BC，直线 MN 经过点 C，且 ADMN 于 D，BEMN 于 E，由此即 可证明 ADCCEB，然后利用全等三角形的性质即可解决问题； （2）由于 ABC 中，ACB=90 ，AC=BC，直线 MN
39、 经过点 C，且 ADMN 于 D，BEMN 于 E，由此仍 然可以证明 ADCCEB，然后利用全等三角形的性质也可以解决问题； （3）当直线 MN 绕点 C 旋转到图（3）的位置时，仍然 ADCCEB，然后利用全等三角形的性质可以 得到 DE=BE-AD 【详解】 解： （1）ABC 中，ACB=90 ， ACD+BCE=90 ， 又直线 MN 经过点 C，且 ADMN 于 D，BEMN 于 E， ADC=CEB=90 ACD+DAC=90 ， BCE=DAC， 在 ADC 和 CEB 中， ADCCEB DACECB ACBC ， ADCCEB（AAS） ， CD=BE，CE=AD， DE
40、=CD+CE=AD+BE； （2）ABC 中，ACB=90 ，直线 MN 经过点 C，且 ADMN 于 D，BEMN 于 E， ADC=CEB=90 ，ACD+BCE=BCE+CBE=90 ， 而 AC=BC， ADCCEB， CD=BE，CE=AD， DE=CE-CD=AD-BE； （3）如图 3， ABC 中，ACB=90 ，直线 MN 经过点 C，且 ADMN 于 D，BEMN 于 E， ADC=CEB=90 ，ACD+BCE=BCE+CBE=90 ， ACD=CBE， AC=BC， ADCCEB， CD=BE，CE=AD， DE=CD-CE=BE-AD； DE、AD、BE 之间的关系为
41、 DE=BE-AD 【点睛】 此题需要考查了全等三角形的判定与性质，也利用了直角三角形的性质，是一个探究性题目，对于学生的 能力要求比较高 26如图 1，图 2，图 3，在ABC中，分别以AB AC，为边，向ABC外作正三角形，正四边形，正五 边形，BECD，相交于点O （正多边形的各边相等，各个内角也相等） 如图 1，求证： ABEADC； 探究：如图 1，BOD= o； 如图 2，BOD= o； 如图 3，BOD= o 【答案】见解析；60 ；90 ；108 【分析】 根据等边三角形的性质可以得出 ABEADC 根据 ABEADC 可得CDA=EBA，根据三角形内角和可得BOD=BAD，从
42、而求解 【详解】 解：证明：如图， ABD 和 AEC 是等边三角， AD=AB，AE=AC，DAB=EAC=ABD=ADB=60 ， DAB+BAC=EAC+BAC， 即DAC=BAE 在 ABE 和 ADC 中， ABAD BAEDAC AEAC ， ABEADC（SAS） ； ABEADC， CDAEBA ， AFD=OFB， BOD=BAD=60 ； 如图， 四边形ABFD和四边形ACGE是正方形， ABAD，AEAC，90BADCAE， 45BDADBA ， BADDAECAEDAE， 即BAECAD， 在ABE和ADC中， ABAD BAEDAC AEAC ， ()ABEADC SAS ， ABEADC， AHB=OHD， BOD=BAD=90 ； 如图，五边形ABHFD和五边形ACIGE是正五边形， ABAD，AEAC， 108BADEAC ， BADDAEEACDAE ，36ABDADB ， BAEDAC， 在ABE和ADC中， ABAD BAEDAC AEAC ， ()ABEADC SAS ， ABEADC， AMB=OMD， BOD=BAD=（5-2） 180 5=108 【点睛】 本题考查了等边三角形的性质的运用，正方形的性质的运用，正五边形的性质的 运用及正n边形的性质的运用，全等三角形的判定及性质的运用，解答时根据正 多边形的性质证明三角形全等是关键
