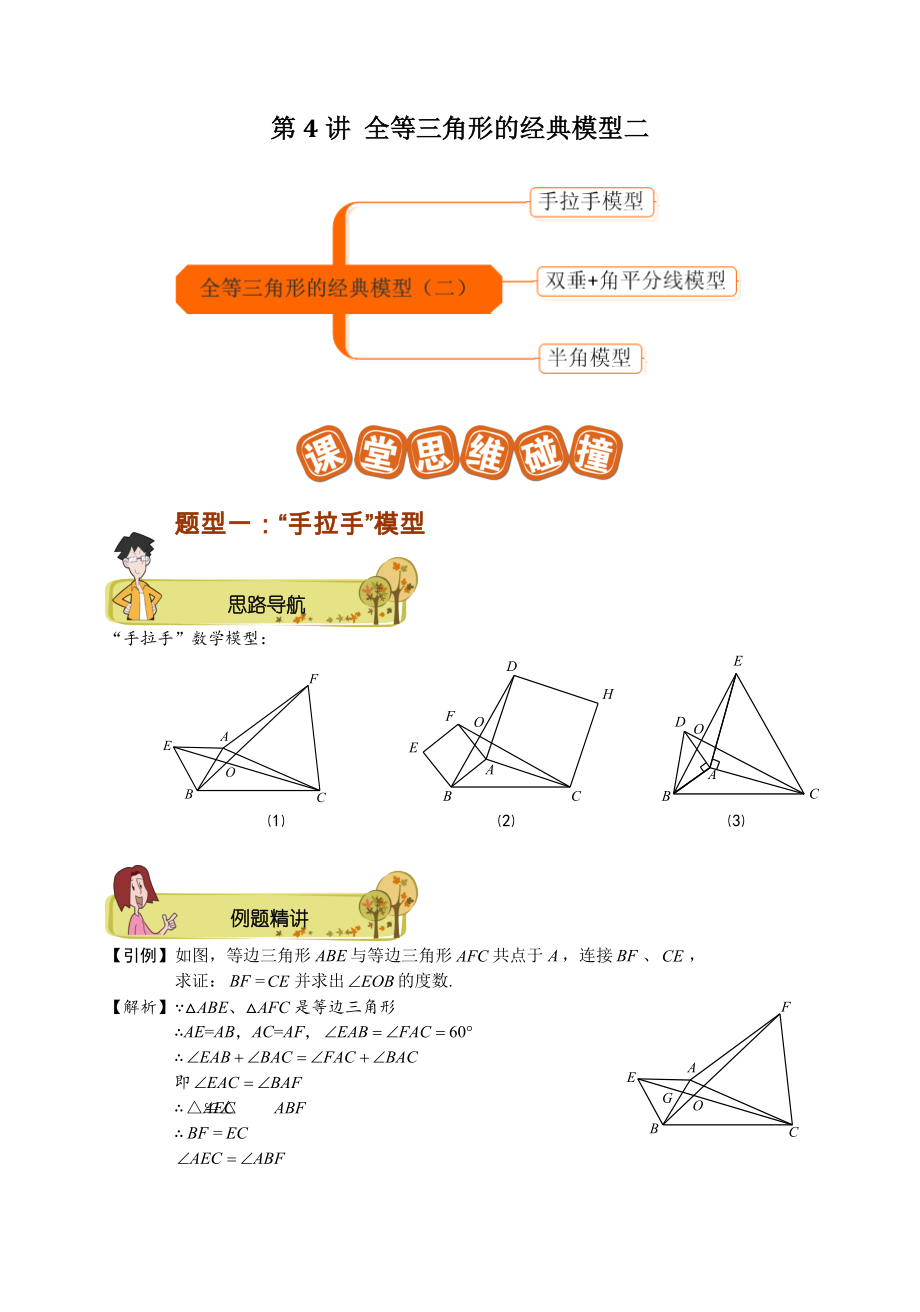
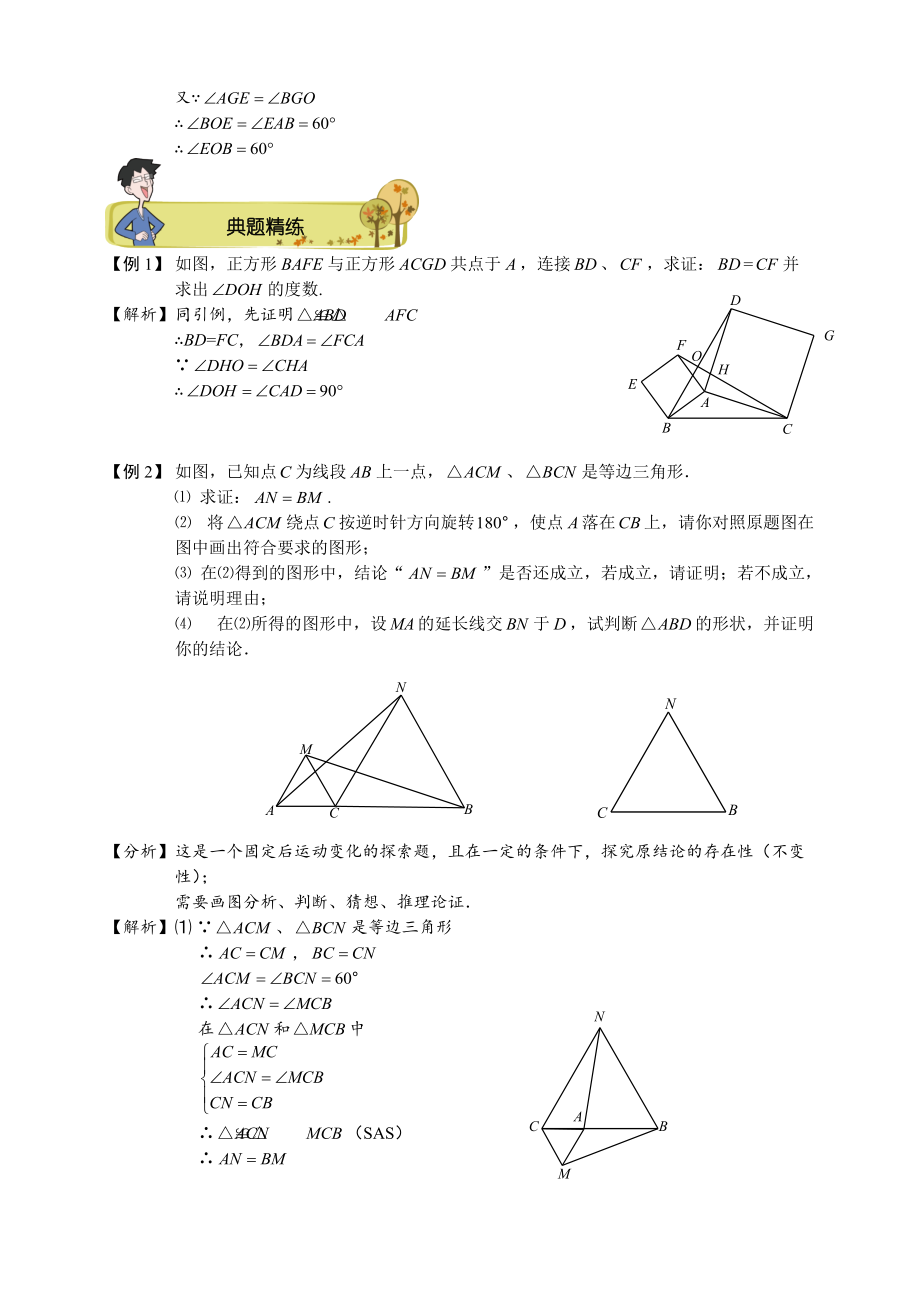
1、第4讲 全等三角形的经典模型二题型一：“手拉手”模型思路导航“手拉手”数学模型： 例题精讲【引例】 如图，等边三角形与等边三角形共点于，连接、，求证：=并求出的度数.【解析】 ABE、AFC是等边三角形 AE=AB，AC=AF，即=又典题精练【例1】 如图，正方形BAFE与正方形ACGD共点于，连接、，求证：=并求出的度数.【解析】 同引例，先证明BD=FC，【例2】 如图，已知点为线段上一点，、是等边三角形 求证：. 将绕点按逆时针方向旋转，使点落在上，请你对照原题图在图中画出符合要求的图形； 在得到的图形中，结论“”是否还成立，若成立，请证明；若不成立，请说明理由； 在所得的图形中，设的延
2、长线交于，试判断的形状，并证明你的结论【分析】 这是一个固定后运动变化的探索题，且在一定的条件下，探究原结论的存在性（不变性）；需要画图分析、判断、猜想、推理论证【解析】 、是等边三角形，在和中 （SAS） 将绕点旋转如图： 在的情况，结论仍然成立证明：，（SAS）， 如图，延长交于，则为等边三角形证明：是等边三角形题型二：双垂+角平分线模型典题精练【例3】 在中，于D，BF平分交AD于E，交AC于F.求证：AE=AF.【解析】 ，是的角平分线【例4】 如图，已知中，于，的角平分线交于，交于，交于求证：【分析】 要证，一般想到证明这两条线段所在的三角形全等，由图形可知，不存在直接全等三角形，因
3、此要想到添加辅助线构造全等三角形【解析】 作于，（角平分线定理）又，又，（AAS），题型三：半角模型典题精练【例5】 已知：正方形中，绕点顺时针旋转，它的两边分别交线段于点.求证. 【解析】 延长到使四边形ABCD是正方形AD=AB在和 AM=AE 在和中MN=ENDE+DN=BM+DN=MN【例6】 如图，在四边形ABCD中，E、F分别是线段BC、CD上的点，且BE+FD=EF. 求证：.【解析】 延长FD到H，使DH=BE，易证，再证【例7】 在等边三角形的两边AB、AC所在直线上分别有两点M、N，D为三角形ABC外一点，且,BD=DC. 探究：当M、N分别在直线AB、AC上移动时，BM、
4、NC、MN之间的数量关系 图1 图2 如图1，当点M、N在边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系是 ； 如图2，点M、N在边AB、AC上，且当DMDN时，猜想问的结论还成立吗？写出你的猜想并加以证明. 【解析】 如图1， BM、NC、MN之间的数量关系 BM+NC=MN 猜想：结论仍然成立证明：如图，延长AC至E，使CE=BM，连接DE BD=CD且又ABC是等边三角形，在与中：(SAS) DM=DE, 在MDN与EDN中：(SAS) 第04讲精讲：典型的旋转全等构图：“手拉手”全等模型探究；【探究一】“手拉手”模型基本构图；如图1，若与旋转全等，则必有与为两个顶角相等
5、的等腰三角形（即相似的等腰三角形）；反之，如图2，若有两个顶角相等的等腰三角形与共顶角顶点，则必有与旋转全等；而图2正是“手拉手”模型的基本构图；【探究二】将探究一中的普通等腰三角形换成特殊的图形，例如等边三角形、等腰直角三角形、正方形，然后再探究结论如何变化；如图3、图4、图5，当两个等边三角形、等腰直角三角形、正方形共顶点时，与仍然旋转全等，并且有两个共同的结论；结论1：；结论2：与所夹锐角等于两个等腰三角形的顶角；（倒角方法如下图6、图7、图8的八字模型）【探究三】将探究二中的特殊图形旋转后结论是否仍然成立；如下图9、图10、图11易得探究二中的两个结论仍然成立；【探究四】深化探究二中图
6、3的结论；如图12，可得结论1：；结论2：；结论3：如图12、图13、图14，可得三对三角形全等（；）结论4：如图15，连接，可得为等边三角形；（由结论3可得）结论5：；（由结论4可得）结论6：连接，可得平分；（如图16，分别作、，与分别是全等三角形与对应边和上的高，故相等）复习巩固题型一 手拉手模型 巩固练习【练习1】 如图，DAAB，EAAC，AD=AB，AE=AC，则下列正确的是（ ） A. B. C. D. 【解析】 D【练习2】 如图，正五边形ABDEF与正五边形ACMHG共点于，连接、，则线段BG、CF具有什么样的数量关系并求出的度数【解析】 先证 可得BG=CF， 题型二 双垂+
7、角平分线模型 巩固练习【练习3】 已知AD平分，垂足为E，,垂足为F，且DB=DC，则EB与FC的关系（ ）A. 相等 B. EBFC D.以上都不对【解析】 A题型三 半角模型 巩固练习【练习4】 如图，ABC是边长为3的等边三角形，BDC是等腰三角形，且BDC120以D为顶点作一个60角，使其两边分别交AB于点M，交AC于点N，连接MN，则AMN的周长为【解析】 6 【练习5】 如图，在四边形中，、分别是边、延长线上的点，且，求证： 【解析】 证明：在上截取，使，连接， ，思维拓展训练(选讲) 训练1. 如图，为线段上一点，分别以、为边在同侧作等边和等边，交于点，交于点，求证：【分析】 本
8、题中，与是等边三角形，因此，因为、在同一条直线上，故这样可以得到，故可以得到，则，所以，故【解析】 和是等边三角形（已知），（等边三角形的各边都相等）（等边三角形的每个角都等于） ，在和中， （SAS）（全等三角形的对应角相等）在和中，（ASA）（全等三角形的对应边相等）（等边对等角）（三角形内角和定理）（等量代换）（内错角相等，两直线平行）训练2. 条件：正方形，在延长线上，在延长线上，结论： ； .【解析】 在CD上取一点Q，使DQ=BM先证可得AM=AQ再证MN=NQ 可证ANHAND，AH=AD=AB训练3. 如图，在中，锐角的平分线交对边于，又交斜边的高于，过引，交于，请问与相等吗？理由是什么？ 【解析】 相等理由如下：如图，过作于平分，平分，（AAS）训练4. 如图，ABD为等腰直角三角形，求证：以、为边的三角形是直角三角形. 【解析】 过B作BD的垂线并取BQ=ND，连接AQ、QM先证再证以、为边的三角形是直角三角形. 课后测测试1. 如图，等腰直角ADB与等腰直角AEC共点于，连接、，则线段BE、CD具有什么样的数量关系和位置关系【解析】 先证明BE=CD，再类似例1倒角即可得到BECD测试2. 如图，ABD为等腰直角三角形，求证：以、为边的三角形是直角三角形. 【解析】 过B作BD的垂线并取BQ=ND，连接AQ、QM先证再证以、为边的三角形是直角三角形.
