1、第第 1818 讲讲 几何变换之旋转（一）几何变换之旋转（一） 一、旋转初步：一、旋转初步： 旋转在生活中很常见，在数学中，旋转变换也是几何三大变换中最常考的一种，也是在近几年中考和 直升外地生考试中频繁出现的热点考点。 1旋转的三要素：旋转角度，旋转中心和旋转方向。 2旋转的性质：旋转前后对应的图形全等，对应的旋转角度相等。 3中心对称：特别的，如果旋转角度为180，那么旋转前后两个图形成中心对称。 注意：注意：两个图形成中心对称和中心对称图形要区别清楚，两个图形成中心对称指的是两个图形，中心 对称图形指的是一个图形，比如说平行四边形是一个中心对称图形。 二、大角夹半角：二、大角夹半角： 大
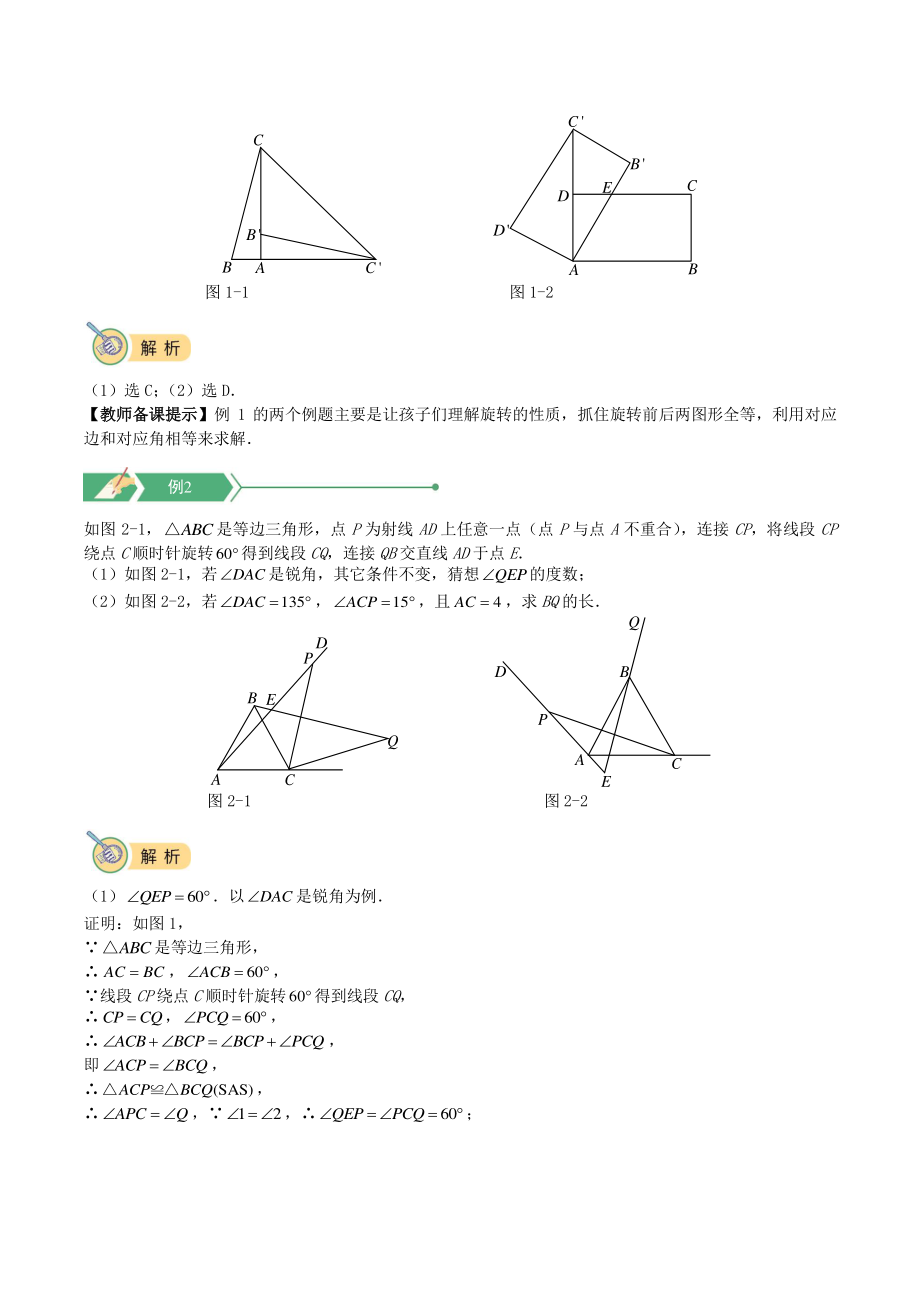
2、角2和半角，比较常见的是90和45，120和60，以90和45为例。 模型模型 I I：正方形中，45EAF，AHEF 可得：可得：BEDFEF；AHAB 模型模型 IIII：等腰直角ABC中，45MAN，可得 222 DNBMMN AD G F B EC H A D N B M Q 模块一 旋转初步 （1）如图 1-1，在RtABC中，90BAC，将ABC绕点顺时针旋转90后得到的ABC （点的对应 点是点B，点的对应点是点C） ，连接CC若32CC B ，则B的大小是（ ） A32 B64 C77 D87 （2）如图 1-2，将矩形绕点旋转至矩形AB C D 位置，此时的中点恰好与点重合，
3、AB交于点若3AB ， 则AEC的面积为（ ） A3 B1.5 C2 3 D3 例1 C CBA B C B BA D D E C 图 1-1 图 1-2 （1）选 C； （2）选 D 【教师备课提示】【教师备课提示】例 1 的两个例题主要是让孩子们理解旋转的性质，抓住旋转前后两图形全等，利用对应 边和对应角相等来求解 如图 2-1，ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合） ，连接CP，将线段CP 绕点C顺时针旋转60得到线段CQ，连接QB交直线AD于点E （1）如图 2-1，若DAC是锐角，其它条件不变，猜想QEP的度数； （2）如图 2-2，若135DAC，15AC
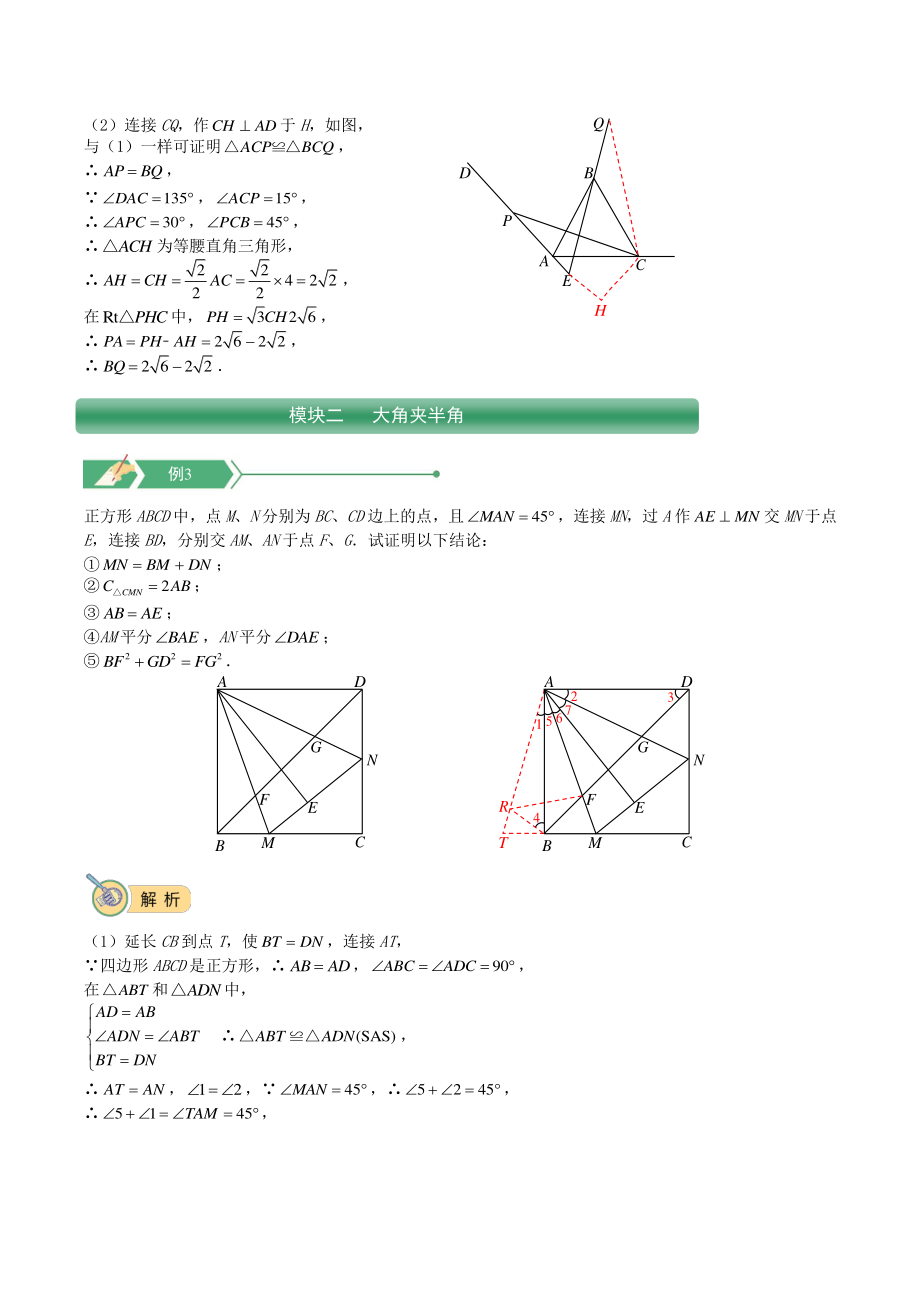
4、P，且4AC ，求BQ的长 C B A Q E P D C B A Q P D E 图 2-1 图 2-2 （1）60QEP以DAC是锐角为例 证明：如图 1， ABC是等边三角形， ACBC，60ACB， 线段CP绕点C顺时针旋转60得到线段CQ， CPCQ，60PCQ， ACBBCPBCPPCQ， 即ACPBCQ， (SAS)ACPBCQ， APCQ ，12 ，60QEPPCQ； 例2 （2）连接CQ，作CHAD于H，如图， 与（1）一样可证明ACPBCQ， APBQ， 135DAC，15ACP， 30APC，45PCB， ACH为等腰直角三角形， 22 42 2 22 AHCHAC， 在
5、RtPHC中，32 6PHCH， 2 62 2PAPHAH， 2 62 2BQ 正方形ABCD中，点M、N分别为BC、CD边上的点，且45MAN，连接MN，过A作AEMN交MN于点 E，连接BD，分别交AM、AN于点F、G试证明以下结论： MNBMDN； 2 CMN CAB ； ABAE； AM平分BAE，AN平分DAE； 222 BFGDFG C A M D B N G F E C A M D B N G F ER T 4 15 6 7 23 （1）延长CB到点T，使BTDN，连接AT， 四边形ABCD是正方形，ABAD，90ABCADC ， 在ABT和ADN中， ADAB ADNABT B
6、TDN (SAS)ABTADN， ATAN，12 ，45MAN，5245 ， 5145TAM ， 模块二 大角夹半角 例3 C B A Q P D E H 在AMT和AMN中， ATAN MANMAT AMAM (SAS)TAMNAM， TMMN，MNBTBMBMDN （2）TAMNAM TMNM， ATMANM SS ABAE； （3）在RtABM和RtAEM ABAE AMAM RtRt()ABMAEM HL，56 17 27 平分 BAE，AN平分DAE； （4）在AT上截取TRNG，连接RB，RF 则有(SAS)TBRNDG RBDG 在ARF和AGF中， ARAG RAFGAF AF
7、AF (SAS)ARFAGF RFGF，4345 ，90RBF， 22 RFRBBF 222 BFGDFG 如图，在正方形ABCD中，E为CD上一动点，连接AE交对角线BD于点F，过点F作FGAE交BC于点G， 连接EG，已知正方形ABCD边长为 4cm，求ECG的周长 C A G D B E F C A G D B E F H 如图，连接CF， 易证(SAS)ABFCBF， AFCF，BAFBCF ， FGAE， 在四边形ABGF中， 3609090180BAFBGF ， 例4 又180BGFCGF， BAFCGF ， CGFBCF ， CFFG， AFFG； AFG是等腰直角三角形， 45
8、EAG， 把ADE顺时针旋转90得到ABH，则AHAE,BHDE,=BAHDAE, AFFG，FGAE， 904545HAGBAGDAE ， EAGHAG ， (SAS)AHGAEG， HGEG， HGBHBGDEBG， 28cm ECG CECEGCGECBGDECGBC 【教师备课提示】【教师备课提示】此题就是需要去先求半角模型，然后再利用半角模型求解 如图， 在直角梯形ABCD中，AD/BC()BCAD，90B，12ABBC，E是AB上的一点， 且45DCE， 4BE ，求DE的长 过C做CGAD交AD延长线于G， 延长AG至F， 使得GFEB CGAD 90AGCAB ABBC 四边形
9、ABCG为正方形 12CGCB， 易证(SAS)BECFGC, ECFC，1= 2 4=45 1+ 3= 2+ 3=45FCD (SAS)ECDFCD EDFD 设EDx 则4DGx，12(4)16ADxx 222 ADAEED 22 6425632xxx 10 x 10DE 例5 D E C B A 在等边ABC的两边AB，AC所在直线上分别有两点M，N，D为ABC外一点， 且60MDN，120BDC， BDCD，探究：当点M，N分别在直线AB，AC上移动时，BM，CN，MN之间的数量关系及AMN的周长Q 与等边ABC的周长L的关系 （1）如图 6-1，当点M，N在边AB，AC上，且DMDN
10、时，BM，NC，MN之间的数量关系式_；此 时 Q L _ （2）如图 6-2，当点，在边，上，且DMDN时，猜想（1）问的两个结论还成立吗？写出你的猜想并加 以证明； （3）如图 6-3，当点M，N分别在边AB，CA的延长线上时，若ANx，则Q _（用x，L表示） 图 6-1 图 6-2 图 6-3 （1）BM + NC = MN； 2 3 Q L （2）猜想：仍然成立，证明：如图，延长AC至E，使CEBM，连接DE， ， 且， ， 由是等边三角形， ， (SAS)MBDECD ， ， ，在与中， ， ，的周长 ， 而等边ABC的周长， （3） 图 M N D CB A 图 M N D C
11、B A N 图 M D C B A BDCD120BDC30DBCDCB ABC90MBDNCD DMDEBDMCDE， DMDE MDNEDN DNDN ()MDNEDN SAS MNNENCBMAMN ()()2QAMANMNAMBMANNCABACAB 3LAB 2 3 Q L 2 2 3 xL 例6 M E N D C B A 如图所示，ABC是边长为 的正三角形，BDC是顶角为120的等腰三角形，以D为顶点作一个60的 MDN，点M、N分别在AB、AC上，求AMN的周长 C A B M D N C A B M D N FE 如图所示，过D作DE交BC于E，使得BEBM；过D作DF交B
12、C于F，使得CFCN 因为120BDC，BDC为等腰三角形，所以30DBC， 又因为ABC为正三角形，所以 30ABC 注意到DBCMBD ，BMBE，BDBD，所以DBEDBM，可知AMCE同理， DCFDCN，ANBF 则有DEDM，DFDN，MDBEDB，NDCFDC 又因为60MDN，120BDC，则180MDBNDC 而120120EDCEDBMDB，120120BDFFDCNDC， 故24060EDCBDFMDBNDC，因此60FDE， 则FDENDM，MNEF，进而可知AMN的周长为 1 【教师备案教师备案】本题是大角夹半角模型的一种变化，可以将条件弱化成D是任意三角形的外心，
13、，结论改成，就变成了一道相当有难度的竞赛题了（第 27 届 全俄奥林匹克题） 如图， 菱形ABCD中， 点E、M在AD上， 且CDCM， 点F为AB上的点， 且 1 2 ECFB.求证：BFEFEM A BC D E F M A BC D E F M N 1 4 3 2 5 1 1 2 MDNBDC AMN CBC 例7 例8 延长AB到N，使BNEM，连接CN CDCM，CDCB，且ABCD BCCM，2ABC 125ABC 15 又BNME，BCCM，BNCMEC 43 ，CENC AD/BC 2BCMABC 1 2 ECFABC 34BCFBCFECF 又NCEC，CFCF NCFECF
14、 FNEFFBNBFBEM FBEFEM. （1）如图 1-1，边长为 6 正方形绕点B按顺时针方向旋转30后得到正方形EBGF，EF交CD于点H，则FH 的长为_（结果保留根号） （2） 如图 1-2， 在同一平面内， 将ABC绕点旋转40到ABC 的位置， 使得CCAB ， 则 B A C （ ） A30 B40 C70 D80 图 1-1 图 1-2 （1）62 3；（2）A 30 H G F E D C B A C C AB B 模块一模块一 旋转初步旋转初步 演练1 演练2 复习巩固 如图，ABC中，1ABAC，45BAC，AEF是由ABC绕点A按顺时针方向旋转得到的，连 接BE、C
15、F相交于点D （1）求证：BECF； （2）当四边形ACDE为菱形时，求BD的长 （1）证明：AEF是由ABC绕点A按顺时针方向旋转得到的，AEAB， AFAC，EAFBAC ， EAFBAFBACBAF ，即EABFAC ， ABAC，AEAF，AEB可由AFC绕点A按顺时针方向旋转得到， BECF； （2）解：四边形ACDE为菱形，1ABAC，1DEAEACAB，ACDE， AEBABE，45ABEBAC ，45AEBABE ， ABE为等腰直角三角形，2= 2BEAC，21BDBEDE 已知梯形ABCD中，ADBC，ABBCDC， 点E、F分别在AD、AB上， 且 1 = 2 FCEBC
16、D （1）求证：BFEFED； （2）连接AC，若80B，70DEC，求ACF的度数 （1）证明：旋转BCF使BC与CD重合， ADBC，ABDC，即梯形ABCD为等腰梯形， AADC ，180AABC ， 180ADCABC ， 由旋转可知：ABCCDF ， 180ADCCDF ，即ADF为平角， A，D，F共线， FCF C，ECEC， ECFBCFDCEECF ， FCEF CE， EFEFDFED， BFEFED； （2）解：ABBC，80B， 50ACB， 由（1）得70FECDEC ， 70ECB， 而80BBCD ， 模块二模块二 大角夹半角大角夹半角 演练3 E A F D B
17、 C B AED F C F B AED F C B AED F C 10DCE， 30BCF， 20ACFBCABCF （1）如图 4-1，在四边形ABCD中，ABAD，90BD，E、F分别是边BC、CD上的点，且 1 2 EAFBAD求证：EFBEFD （2）如图 4-2，在四边形ABCD中，ABAD，180BD，E、F分别是边BC、CD上的点，且 1 2 EAFBAD， （1）中的结论是否仍然成立？不用证明 （3）如图 4-3，在四边形ABCD中，ABAD，180BD，E、F分别是边BC、CD延长线上的点，且 1 2 EAFBAD， （1） 中的结论是否仍然成立？若成立， 请证明； 若不
18、成立， 请写出它们之间的数量关系， 并证明 A D F BEC A B E C F D A B F D C E 图 4-1 图 4-2 图 4-2 （1）延长EB到G，使BGDF，连接AG 90ABGABCD，ABAD， ABGADFAGAF，12 1 1323 2 EAFBAD GAEEAF又AEAE， AEGAEFEGEF EGBEBGEFBEFD （2） （1）中的结论EFBEFD仍然成立 （3）结论EFBEFD不成立，应当是EFBEFD 证明：在BE上截取BG，使BGDF，连接AG 180BADC，180ADFADC， BADFABAD， ABGADFBAGDAF，AGAF 1 2 B
19、AGEADDAFEADEAFBAD GAEEAFAEAE，AEGAEF 演练4 EGEF，EGBEBG，EFBEFD A D F BECG 13 2 A B F D C E G 如图，已知正方形ABCD的边长为 1，P、Q是其内两点，且45PAQPCQ求 P A BP C QQ A D SSS 的 值 如图，将绕点A顺时针旋转至处， 使与重合，连接 将绕点逆时针旋转至处， 使与重合，连接 由旋转可知： ， 又 又， （SAS） APQAPM SS APQBMPPCQ SSS 同理：， ， ， 又， （SSS） ADQ90 ABM ADABPM CQDC90CBN CDCBPN ABMADQ A
20、MAQQDMBMABQAD ABMADQ SS 1 45 2 PAQBAD 45MAPMABPABQADPAB PAQMAP AQAM APAP APQAPM PMPQ PABPCQQAD SSS PABPCQMAB SSS AMPBMPPCQ SSS CDQCBNCPQCPN BMQDPNPQ BNQDPNPQ QCDAPQBPC SSS BCNAPQBPC SSS CNBNPAPQ SSS P PCQBNPAPQ SSS BPBPBMBN PMPNPQ PBMPBN 演练5 A BC D M N P P D CB A Q PBMPBN SS PABPCQQADQCDAPQBPC SSSSSS 11 22 PABPCQQADABCD SSSS 正方形
