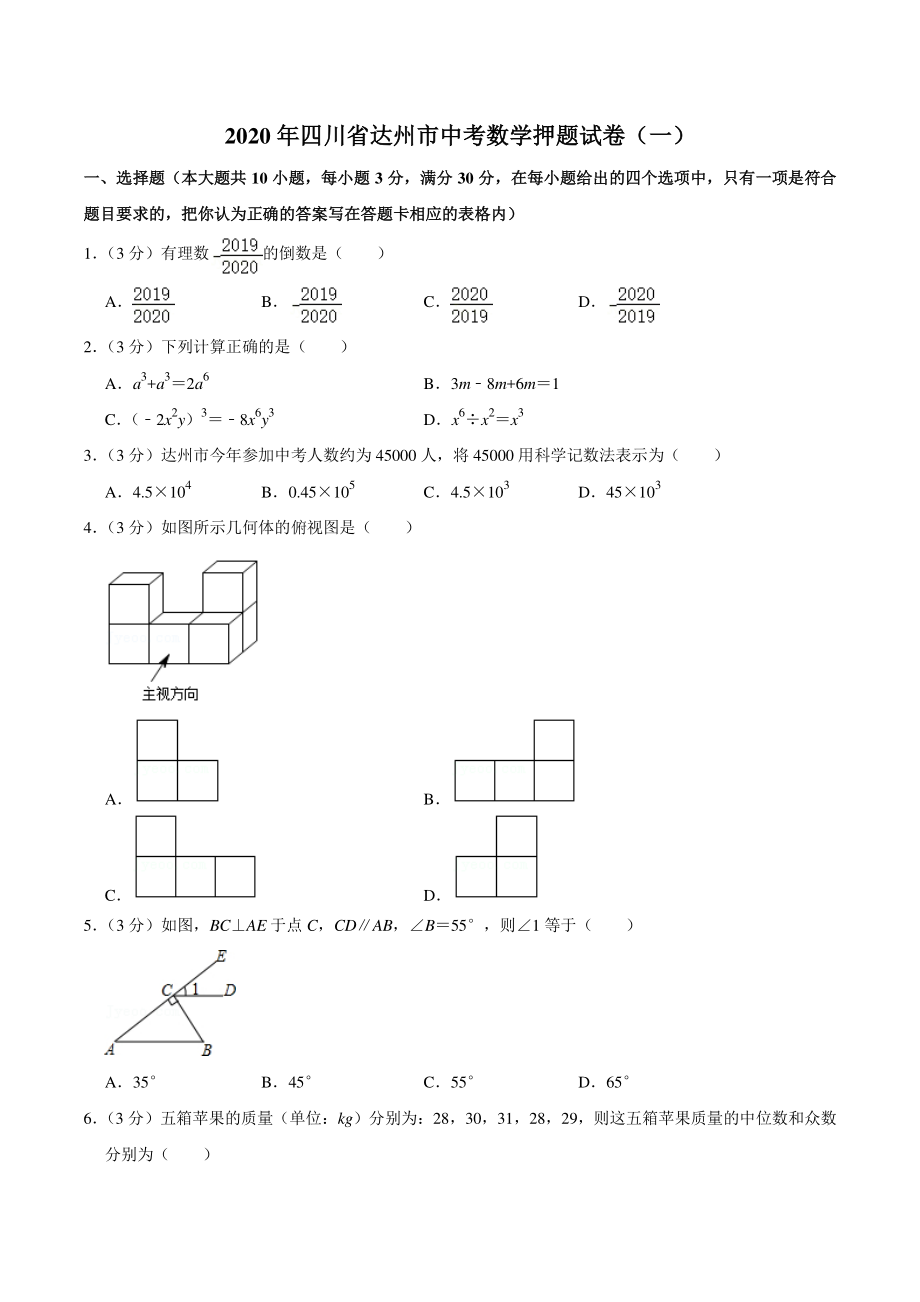
 2020年四川省达州市中考数学押题试卷(一)含答案详解
2020年四川省达州市中考数学押题试卷(一)含答案详解
《2020年四川省达州市中考数学押题试卷(一)含答案详解》由会员分享,可在线阅读,更多相关《2020年四川省达州市中考数学押题试卷(一)含答案详解(27页珍藏版)》请在七七文库上搜索。
1、 2020 年四川省达州市中考数学押题试卷(一)年四川省达州市中考数学押题试卷(一) 一、选择题(本大题共一、选择题(本大题共 10 小题,每小题小题,每小题 3 分,满分分,满分 30 分,在每小题给出的四个选项中,只有一项是符合分,在每小题给出的四个选项中,只有一项是符合 题目要求的,把你认为正确的答案写在答题卡相应的表格内)题目要求的,把你认为正确的答案写在答题卡相应的表格内) 1 (3 分)有理数的倒数是( ) A B C D 2 (3 分)下列计算正确的是( ) Aa3+a32a6 B3m8m+6m1 C (2x2y)38x6y3 Dx6x2x3 3 (3 分)达州市今年参加中考人数
2、约为 45000 人,将 45000 用科学记数法表示为( ) A4.5104 B0.45105 C4.5103 D45103 4 (3 分)如图所示几何体的俯视图是( ) A B C D 5 (3 分)如图,BCAE 于点 C,CDAB,B55,则1 等于( ) A35 B45 C55 D65 6 (3 分)五箱苹果的质量(单位:kg)分别为:28,30,31,28,29,则这五箱苹果质量的中位数和众数 分别为( ) A30 和 28 B30 和 29 C28 和 28 D29 和 28 7 (3 分)若关于 x 的方程 x22(m+1)x+m2+30 有实数根,则反比例函数 y与一次函数
3、ymx+m 的图象大致是( ) A B C D 8 (3 分)如图,在ABC 中,ABAC16,D 是 BC 边上一点,E 是 AC 边上一点,ADEC,CE: BD3:4,则 CD 的长为( ) A12 B10 C8 D6 9 (3 分)小华在学习“锐角三角函数”时发现,将如图所示的矩形纸片 ABCD 沿过点 B 的直线折叠,使 点 A 落在 BC 上的点 E 处,还原后,再沿过点 E 的直线折叠,使点 A 落在 BC 上的点 F 处,这样就可以 求出 22.5角的正切值是( ) A1 B+1 C+1 D1 10 (3 分)已知二次函数 yax2+bx+c(a0)的图象如图所示,则下列结论:
4、3a+b0;ab+c0; c0;a+b0其中正确的结论有( ) A仅 B仅 C仅 D 二、填空题(本大题共二、填空题(本大题共 6 小题,每小题小题,每小题 3 分,满分分,满分 18 分)分) 11 (3 分)函数 y中自变量 x 的取值范围是 12 (3 分)分解因式:3x212 13 (3 分) 为了丰富学生课余生活, 达州市某中学计划开设以下社团: A 足球, B 机器人, C 航模, D 绘 画,学校要求每人只能参加一个社团,小丽和小亮准备随机报名一个项目,则两人至少有一人参加“航 模”社团的概率为 14 (3 分)如图,在AOB 中,AOB90,tanOAB2,点 A 在反比例函数
5、 y的图象上,若点 B 在反比例函数 y的图象上,则 k 15 (3 分)如图,在平面直角坐标系中,若矩形 OABC 的边 OA 与 x 轴正半轴的夹角为 30,OC6,OA 12则点 B 的坐标为 16 (3 分)如图,在O 中,AB 是直径,D 是O 上一点,C 是的中点,弦 CEAB 于点 F,过点 D 的 切线交 EC 的延长线于点 G,连接 AD,分别交 CF,BC 于点 P,Q,连接 AC给出下列结论:BAD 2CAD;GPGD;AQ2PC;AFABCQCB;AQACQCBA其中正确的是 (写出所有正确结论的序号) 三、解答题(本大题共三、解答题(本大题共 9 小题,满分小题,满分
6、 72 分,解答时应写出必要的文字说明、证明过程或演算步骤)分,解答时应写出必要的文字说明、证明过程或演算步骤) 17 (6 分)计算:|3|+2cos30+() 1+( )0+ 18 (6 分)先化简,后计算:,其中 x2+x3 19 (7 分)为创建“国家园林城市” ,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对 200 名 同学的参赛作品打分发现,参赛者的成绩 x 均满足 50 x100,并制作了频数分布直方图,如图 根据以上信息,解答下列问题: (1)请补全频数分布直方图; (2)若依据成绩,采取分层抽样的方法,从参赛同学中抽 40 人参加图片制作比赛总结大会,则从成绩 80
7、 x90 的选手中应抽多少人? (3)比赛共设一、二、三等奖,若只有 25%的参赛同学能拿到一等奖,则一等奖的分数线是多少? 20 (7 分)我市为创建“国家级森林城市” ,政府对江边一处荒地进行绿化,要求栽植腊梅、黄葛两种不同 的树苗共 6000 棵,且腊梅树苗不得多于黄葛树苗某承包商以 35 万元的报价中标承包了这项工程根 据调查及相关资料表明: 移栽一棵树苗的平均费用为 8 元, 腊梅、 黄葛两种树苗的购买价及成活率如表: 品种 购买价(元/棵) 成活率 腊梅树 20 90% 黄葛树 50 95% 设购买腊梅树苗 x 棵,承包商获得的利润为 y 元请根据以上信息解答下列问题: (1)设
8、y 与 x 之间的函数关系式,并写出自变量的取值范围; (2)承包商要获得不低于中标价 16%的利润,应如何选购树苗? (3)政府与承包商的合同要求规定:栽植这批树苗的成活率不得低于 93%,否则承包商出资补栽;若成 活率达到 94%以上(含 94%) ,则政府另给予中标价的 6%作为奖励,该承包商应如何选购树苗才能获得 最大利润?最大利润为多少? 21 (7 分)如图,直线 yx+b(b0)与双曲线 y(x0)交于点 A,与 x轴交于点 B,OA 与 x 轴 的正半轴的夹角为 ,且 OA2OB26,tan3,求一次函数和反比例函数的解析式 22 (8 分)如图,在一条笔直的公路 MN 的同侧
9、有 A,B 两个山头,为了测量这两个山头之间的距离,在 公路 MN 上选取点 C,在点 C 处测得ACM60,BCN45,从点 C 沿 CN 方向前进 1000 米到 达点 D,在点 D 处测得ADMADB45求 A,B 两个山头之间的距离(结果用根号表示) 23 (9 分)如图,AB 为O 的直径,CD 为弦,且 CDAB 于点 F,连接 AD,O 的半径为 6,弦 CD 6 (1)试判断ACD 的形状,并说明理由; (2)若 E 为的中点,连接 CE 交 AB 于点 G求 CECG 的值 24 (10 分)如图,四边形 ABCD 中,AB90,AD2,AB5,BC3 (1)如图,P 为 A
10、B 边上的一动点,以 PD,PC 为边作PCQD 请问四边形 PCQD 能否为矩形,若能,求出 AP 的长;若不能,请说明理由; 当 AP 时,四边形 PCQD 为菱形; 当 AP 时,四边形 PCQD 有四条对称轴 (2)如图,若 P 为 AB 边上一点,以 PD,PC 为边作PCQD,请问对角线 PQ 的长是否存在最小值? 如果存在,请求出最小值;如果不存在,请说明理由 (3) 如图, 若 P 为 DC 边上任意一点, 延长 PA 到 E, 使 AEnPA (n 为常数) , 以 PE, PB 为边作PBQE, 请探究对角线 PQ 的长是否也存在最小值?如果存在,请求出最小值;如果不存在,
11、请说明理由 25 (12 分)如图,在平面直角坐标系中,矩形 ABCD 的三个顶点 B(1,0) ,C(3,0) ,D(3,4) 以 A 为顶点的抛物线 yax2+bx+c 过点 C,动点 P 从点 A 出发,沿线段 AB 向点 B 运动,同时动点 Q 从点 C 出发,沿线段 CD 向点 D 运动,点 P,Q 的运动速度均为每秒 1 个单位长度,运动时间为 t 秒过点 P 作 PEAB 交 AC 于点 E (1)直接写出点 A 的坐标,并求出抛物线的表达式; (2)过点 E 作 EFAD 于点 F,交抛物线于点 G,当 t 为何值时,ACG 的面积最大?最大值为多少? (3)在动点 P,Q 运
12、动的过程中当 t 为何值时,在矩形 ABCD 内(包括边界)存在点 H,使以 C,Q, E,H 为顶点的四边形为菱形?请直接写出 t 的值 2020 年四川省达州市中考数学押题试卷(一)年四川省达州市中考数学押题试卷(一) 参考答案与试题解析参考答案与试题解析 一、选择题(本大题共一、选择题(本大题共 10 小题,每小题小题,每小题 3 分,满分分,满分 30 分,在每小题给出的四个选项中,只有一项是符合分,在每小题给出的四个选项中,只有一项是符合 题目要求的,把你认为正确的答案写在答题卡相应的表格内)题目要求的,把你认为正确的答案写在答题卡相应的表格内) 1 (3 分)有理数的倒数是( )
13、A B C D 【解答】解:()()1, 有理数的倒数是, 故选:D 2 (3 分)下列计算正确的是( ) Aa3+a32a6 B3m8m+6m1 C (2x2y)38x6y3 Dx6x2x3 【解答】解:A、a3+a32a3,故此选项错误; B、3m8m+6mm,故此选项错误; C、 (2x2y)38x6y3,正确; D、x6x2x4,故此选项错误; 故选:C 3 (3 分)达州市今年参加中考人数约为 45000 人,将 45000 用科学记数法表示为( ) A4.5104 B0.45105 C4.5103 D45103 【解答】解:450004.5104, 故选:A 4 (3 分)如图所示
14、几何体的俯视图是( ) A B C D 【解答】解:从上边看有两层,底层是三个正方形,上层的右边是一个正方形 故选:B 5 (3 分)如图,BCAE 于点 C,CDAB,B55,则1 等于( ) A35 B45 C55 D65 【解答】解:如图,BCAE, ACB90 A+B90 又B55, A35 又 CDAB, 1A35 故选:A 6 (3 分)五箱苹果的质量(单位:kg)分别为:28,30,31,28,29,则这五箱苹果质量的中位数和众数 分别为( ) A30 和 28 B30 和 29 C28 和 28 D29 和 28 【解答】解:将这组数按小到大排列:28,28,29,30,31,
15、则中位数为 29, 28 出现了 2 次,出现的次数最多, 众数为 28 故选:D 7 (3 分)若关于 x 的方程 x22(m+1)x+m2+30 有实数根,则反比例函数 y与一次函数 ymx+m 的图象大致是( ) A B C D 【解答】解:关于 x 的方程 x22(m+1)x+m2+30 有实数根, 2(m+1)24(m2+3)0 解得 m1, 反比例函数 y的图象在一三象限,一次函数 ymx+m 的图象经过一二四象限, 故选:B 8 (3 分)如图,在ABC 中,ABAC16,D 是 BC 边上一点,E 是 AC 边上一点,ADEC,CE: BD3:4,则 CD 的长为( ) A12
16、 B10 C8 D6 【解答】解:如图, ABAC, BC, ADEC, ADB180ADECDE, DEC180CCDE, ADBDEC, ABDDCE, , AB16,CE:BD3:4, , DC12 故选:A 9 (3 分)小华在学习“锐角三角函数”时发现,将如图所示的矩形纸片 ABCD 沿过点 B 的直线折叠,使 点 A 落在 BC 上的点 E 处,还原后,再沿过点 E 的直线折叠,使点 A 落在 BC 上的点 F 处,这样就可以 求出 22.5角的正切值是( ) A1 B+1 C+1 D1 【解答】解:将如图所示的矩形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 上的
17、点 E 处, ABC90,ABBE, AEBEAB45, 还原后,再沿过点 E 的直线折叠,使点 A 落在 BC 上的点 F 处, AEEF,EAFEFAAEB22.5, 设 ABx,则 AEEFx,BFBE+EFx+x, tanAFBtan22.51, 故选:A 10 (3 分)已知二次函数 yax2+bx+c(a0)的图象如图所示,则下列结论:3a+b0;ab+c0; c0;a+b0其中正确的结论有( ) A仅 B仅 C仅 D 【解答】解:抛物线开口方向向下,则 a0, 对称轴是直线 x1,则 b2a, 3a+b3a2aa0,故正确; 当 x1 时,y0,即 ab+c0,故正确; 抛物线与
18、 y 轴交于正半轴,则 c0,故正确; b2a, a+ba2aa, a0, a0, a+b0,故正确 综上所述,正确的结论是: 故选:D 二、填空题(本大题共二、填空题(本大题共 6 小题,每小题小题,每小题 3 分,满分分,满分 18 分)分) 11 (3 分)函数 y中自变量 x 的取值范围是 x2 且 x1 【解答】解:由题意得,x+20 且 x10, 解得 x2 且 x1 故答案为:x2 且 x1 12 (3 分)分解因式:3x212 3(x2) (x+2) 【解答】解:原式3(x24) 3(x+2) (x2) 故答案为:3(x+2) (x2) 13 (3 分) 为了丰富学生课余生活,


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2020 四川省 达州市 中考 数学 押题 试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 2021年四川省达州市中考物理真题含答案
- 2021年四川省达州市中考数学全真模拟试卷二含答案
- 2020年四川省达州市中考语文试题含答案
- 2018年四川省达州市中考数学试卷含答案解析
- 2020年四川省达州市中考道德与法治试题含答案
- 2020年四川省各市中考数学真题压轴题圆含答案
- 2020年四川省达州市中考物理试卷含详细解答
- 2017年四川省达州市中考数学试卷含答案解析
- 2021年四川省达州市中考历史模拟卷一含答案
- 2020年四川省达州市中考数学试卷含详细解答
- 2021达州数学
- 2020年四川省达州市中考英语试卷含答案解析
- 2022年四川省达州市中考模拟冲刺语文试卷一含答案
- 2020年四川省达州市中考数学押题试卷一含答案详解
- 2020年达州中考语文试卷
- 2020年四川省达州市中考语文试卷
- 2020年四川省达州市中考生物试题
- 2021年四川省达州市中考英语真题
- 2022年四川省达州市中考英语真题
- 2020年四川省达州市中考生物试卷



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-189263.html