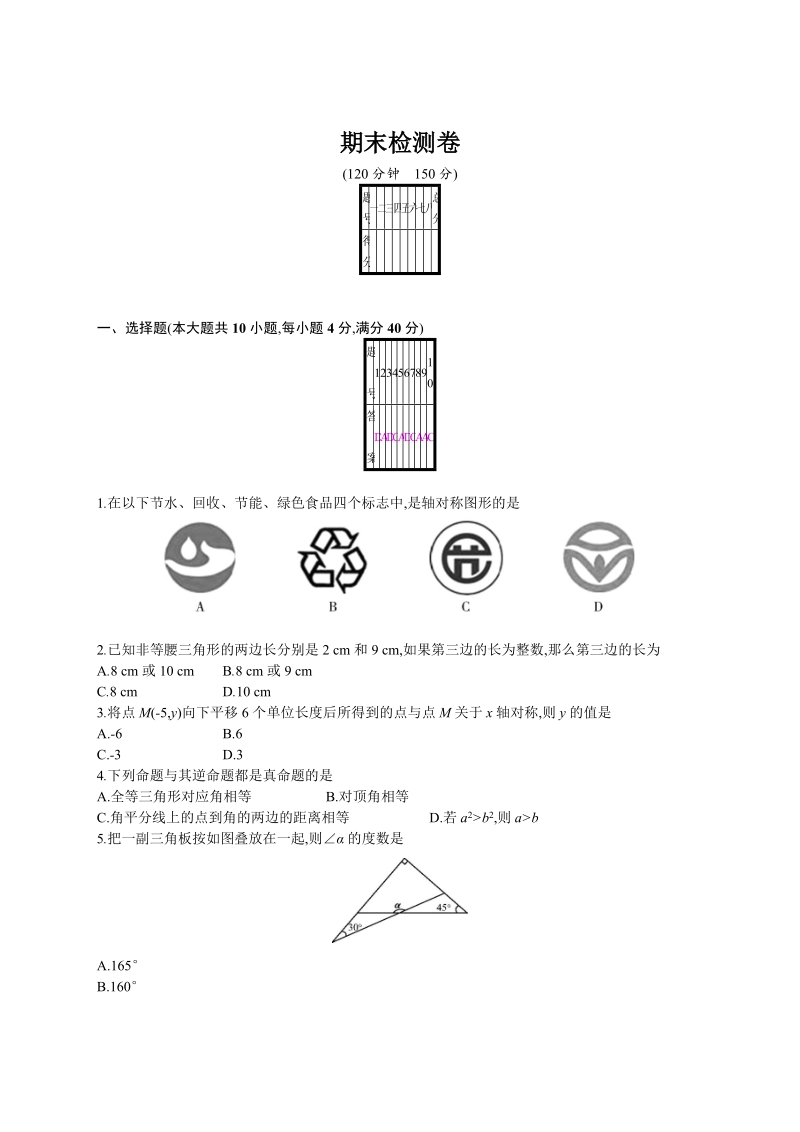
1、期末检测卷(120 分钟 150 分)题号 一 二 三 四 五 六 七 八总分得分一、选择题(本大题共 10 小题 ,每小题 4 分,满分 40 分)题号12345678910答案DADCADCAAC1.在以下节水、回收、节能、绿色食品四个标志中,是轴对称图形的是2.已知非等腰三角形的两边长分别是 2 cm 和 9 cm,如果第三边的长为整数,那么第三边的长为A.8 cm 或 10 cm B.8 cm 或 9 cmC.8 cm D.10 cm3.将点 M(-5,y)向下平移 6 个单位长度后所得到的点与点 M 关于 x 轴对称,则 y 的值是A.-6 B.6C.-3 D.34.下列命题与其逆命
2、题都是真命题的是A.全等三角形对应角相等 B.对顶角相等C.角平分线上的点到角的两边的距离相等 D.若 a2b2,则 ab5.把一副三角板按如图叠放在一起,则 的度数是A.165B.160C.155D.1506.如图,点 A,D,C,F 在一条直线上,AB=DE,A=EDF,下列条件不能判定ABC DEF 的是A.AD=CFB.BCA=FC.B=ED.BC=EF7.已知函数 y=kx+b 的图象如图所示 ,则函数 y=-bx+k 的图象大致是8.如图,点 E 是 BC 的中点,ABBC ,DCBC ,AE 平分BAD,下列结论: AED=90; ADE= CDE; DE=BE; AD=AB+C
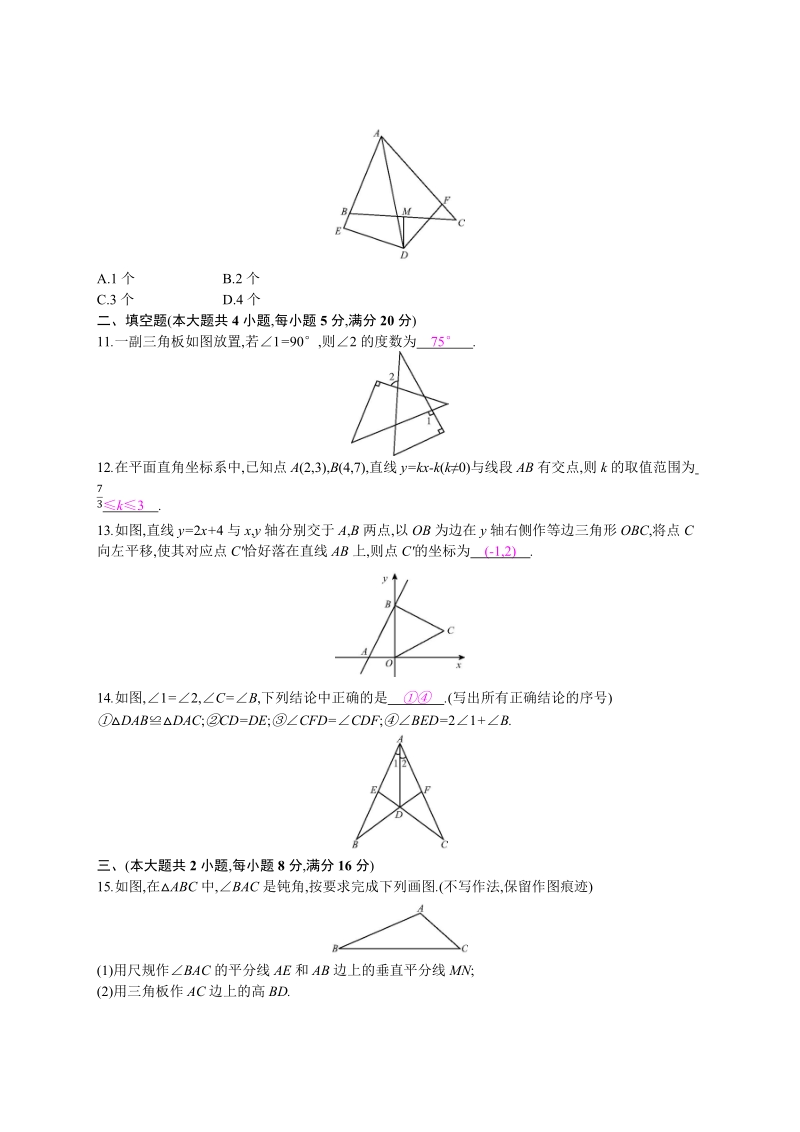
3、D.其中正确的是A.B.C.D.9.如图,已知直线 mn,在某平面直角坐标系中 ,x 轴直线 m,y 轴直线 n,点 A,B 的坐标分别为(-4,2),(2,-4),点 A,O4,B 在同一条直线上 ,则坐标原点为A.O1 B.O2 C.O3 D.O410.如图,ABC 中,BAC=60 ,BAC 的平分线 AD 与边 BC 的垂直平分线 MD 相交于点D,DEAB 交 AB 的延长线于点 E,DFAC 于点 F,现有下列结论: DE=DF; DE+DF=AD; DM 平分ADF; AB+AC=2AE.其中正确的有A.1 个 B.2 个C.3 个 D.4 个二、填空题(本大题共 4 小题 ,每
4、小题 5 分,满分 20 分)11.一副三角板如图放置,若1=90,则2 的度数为 75 . 12.在平面直角坐标系中,已知点 A(2,3),B(4,7),直线 y=kx-k(k0)与线段 AB 有交点,则 k 的取值范围为 k3 . 7313.如图,直线 y=2x+4 与 x,y 轴分别交于 A,B 两点,以 OB 为边在 y 轴右侧作等边三角形 OBC,将点 C向左平移,使其对应点 C恰好落在直线 AB 上,则点 C的坐标为 (-1,2) . 14.如图,1=2,C= B ,下列结论中正确的是 .(写出所有正确结论的序号) DABDAC; CD=DE; CFD=CDF; BED=21+ B
5、.三、(本大题共 2 小题,每小题 8 分,满分 16 分)15.如图,在ABC 中,BAC 是钝角 ,按要求完成下列画图.(不写作法,保留作图痕迹)(1)用尺规作BAC 的平分线 AE 和 AB 边上的垂直平分线 MN;(2)用三角板作 AC 边上的高 BD.解:如图所示.16.如图,在边长为 1 个单位长度的小正方形组成的网格中,给出了平面直角坐标系及格点AOB.(顶点是网格线的交点)(1)画出将AOB 沿 y 轴翻折得到的 AOB1,则点 B1 的坐标为 (-3,0) ; (2)画出将AOB 沿射线 AB1 方向平移 2.5 个单位得到的A 2O2B2,则点 A2 的坐标为 (-1.5,
6、2) ; (3)请求出AB 1B2 的面积.解:(1)AOB 1 如图所示.(2)A2O2B2 如图所示.(3)AB1B2 的面积=4.56- 34- 1.56- 4.52=12.12 12 12四、(本大题共 2 小题,每小题 8 分,满分 16 分)17.如图,已知 CD 是 AB 的中垂线,垂足为 D,DEAC 于点 E,DFBC 于点 F.(1)求证:DE=DF;(2)若线段 CE 的长为 3 cm,BC 的长为 4 cm,求 BF 的长.解:(1) CD 是 AB 的中垂线, AC=BC, ACD=BCD, DEAC,DFBC, DE=DF.(2) DEAC,DFBC, AED=BF
7、D=90,在 RtADE 和 RtBDF 中, =,=, RtADERtBDF(HL), AE=BF, CE=3 cm,BC=4 cm, BF=AE=AC-CE=BC-CE=1 cm.18.已知:如图 1,在 RtABC 和 RtABC中,AB=AB,AC=AC,C=C= 90.求证:RtABC 和 RtABC全等.(1)请你用“如果,那么”的形式叙述上述命题;(2)将ABC 和 ABC拼在一起,请你画出两种拼接图形;例如图 2:(即使点 A 与点 A重合,点 C 与点 C重合.)(3)请你选择你拼成的其中一种图形,证明该命题.解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的
8、斜边和一条直角边分别相等,那么这两个直角三角形全等.(2)如图:图 使点 A 与点 A重合,点 B 与点 B重合.图 使点 A 与点 B重合,点 B 与点 A重合.(3)在图 中, 点 A 和点 A重合 ,点 B 和点 B重合,连接 CC. AC=AC, ACC=ACC , ACB=ACB=90, ACB- ACC=ACB- ACC,即BCC=BCC, BC=BC.在 RtABC 和 RtABC中, =,=,=, ABCABC(SSS) .五、(本大题共 2 小题,每小题 10 分,满分 20 分)19.小明平时喜欢玩“宾果消消乐”游戏.本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如
9、下表:月份 x 910111213(第二年元月)14(第二年 2月)成绩y(分 )90 80 70 60 (1)以月份为 x 轴,成绩为 y 轴,根据上表提供的数据在平面直角坐标系中描点;(2)观察(1)中所描点的位置关系,猜想 y 与 x 之间的函数关系,并求出所猜想的函数表达式;(3)若小明继续沉溺于“宾果消消乐”游戏,照这样的发展趋势,请你估计元月(此时 x=13)份的考试中小明的数学成绩,并用一句话对小明提出一些建议.解:(1)如图.(2)猜想:y 是 x 的一次函数 .设 y=kx+b,把点(9,90),(10,80)代入得 解得 y=-10x+180.9+=90,10+=80, =
10、-10,=180,经验证,点(11,70)和(12,60) 均在直线 y=-10x+180 上, y 与 x 之间的函数表达式为 y=-10x+180.(3) 当 x=13 时,y=50, 估计元月份的考试中小明的数学成绩是 50 分.建议:不要再沉迷于游戏,要好好学习 .20.如图,在 Rt ABC 中,ACB=90,A=22.5,斜边 AB 的垂直平分线交 AC 于点 D,点 F 在 AC 上,点E 在 BC 的延长线上,CE=CF,连接 BF,DE.则线段 DE 和 BF 在数量和位置上有什么关系?请说明理由.解:DE=BF,DE BF.理由如下 :连接 BD,延长 BF 交 DE 于点
11、 G. 点 D 在线段 AB 的垂直平分线上 , AD=BD, ABD=A=22.5.在 Rt ABC 中, ACB=90,A=22.5, ABC=67.5, CBD=ABC-ABD=45, BCD 为等腰直角三角形, BC=DC.在ECD 和FCB 中, =,=,=, ECDFCB(SAS ), DE=BF,CED= CFB. CFB+CBF=90, CED+CBF=90, EGB= 90,即 DEBF.六、(本题满分 12 分)21.某学校开展“青少年科技创新比赛”活动,“ 喜洋洋”代表队设计了一个遥控车沿直线轨道 AC 做匀速直线运动的模型.甲、乙两车同时分别从 A,B 出发,沿轨道到达
12、 C 处,在 AC 上,甲的速度是乙的速度的 1.5 倍,设 t 分后甲、乙两遥控车与 B 处的距离分别为 d1,d2(单位:米),则 d1,d2 与 t 的函数关系如图,试根据图象解决下列问题.(1)填空:乙的速度 v2= 40 米/分; (2)写出 d1 与 t 的函数表达式;(3)若甲、乙两遥控车的距离超过 10 米时信号不会产生相互干扰 ,试探究什么时间两遥控车的信号不会产生相互干扰?解:(2)v 1=1.5v2=1.540=60(米/ 分),6060=1(分钟),a=1, d1=-60+60 (010,解得 t10,解得 t2.5,所以 1t2.5 时,两车不会产生信号干扰 . 当
13、0t2.5 时,两遥控车的信号不会产生相互干扰 .七、(本题满分 12 分)22.在平面直角坐标系 xOy 中 ,已知定点 A(1,0)和 B(0,1).(1)如图 1,若动点 C 在 x 轴上运动,则使ABC 为等腰三角形的点 C 有几个?(2)如图 2,过点 A,B 向过原点的直线 l 作垂线,垂足分别为 M,N,试判断线段 AM,BN,MN 之间的数量关系,并说明理由.解:(1)如图,当以 AB 为腰时,有 3 个; 当以 AB 为底时,有 1 个, 使ABC 为等腰三角形的点 C 有 4 个.(2)AM+BN=MN.理由:由已知可得 OA=OB,AOM=90- BON= OBN,在AO
14、M 和OBN 中, =,=,=, AOMOBN(AAS ), AM=ON,OM=BN, AM+BN=ON+OM=MN.八、(本题满分 14 分)23.如图,在ABC 中,AB=AC, BAC=90,点 P 是 BC 上的一动点,AP=AQ,PAQ=90,连接 CQ.(1)求证:CQ BC.(2)ACQ 能否是直角三角形?若能,请直接写出此时点 P 的位置 ;若不能,请说明理由.(3)当点 P 在 BC 上什么位置时,ACQ 是等腰三角形? 请说明理由.解:(1) BAP+CAP=BAC=90,CAQ+CAP=PAQ=90, BAP=CAQ ,在ABP 和ACQ 中, =,=,=, ABP ACQ(SAS), ACQ=B, AB=AC,BAC=90, B=ACB=45, BCQ=ACB+ACQ=45+ 45=90, CQBC.(2)当点 P 为 BC 的中点或与点 C 重合时,ACQ 是直角三角形.(3) 当 BP=AB 时,ABP 是等腰三角形; 当 AB=AP 时,点 P 与点 C 重合 ; 当 AP=BP 时,点 P 为 BC 的中点 . ABP ACQ, 当点 P 为 BC 的中点或与点 C 重合或 BP=AB 时,ACQ 是等腰三角形.
