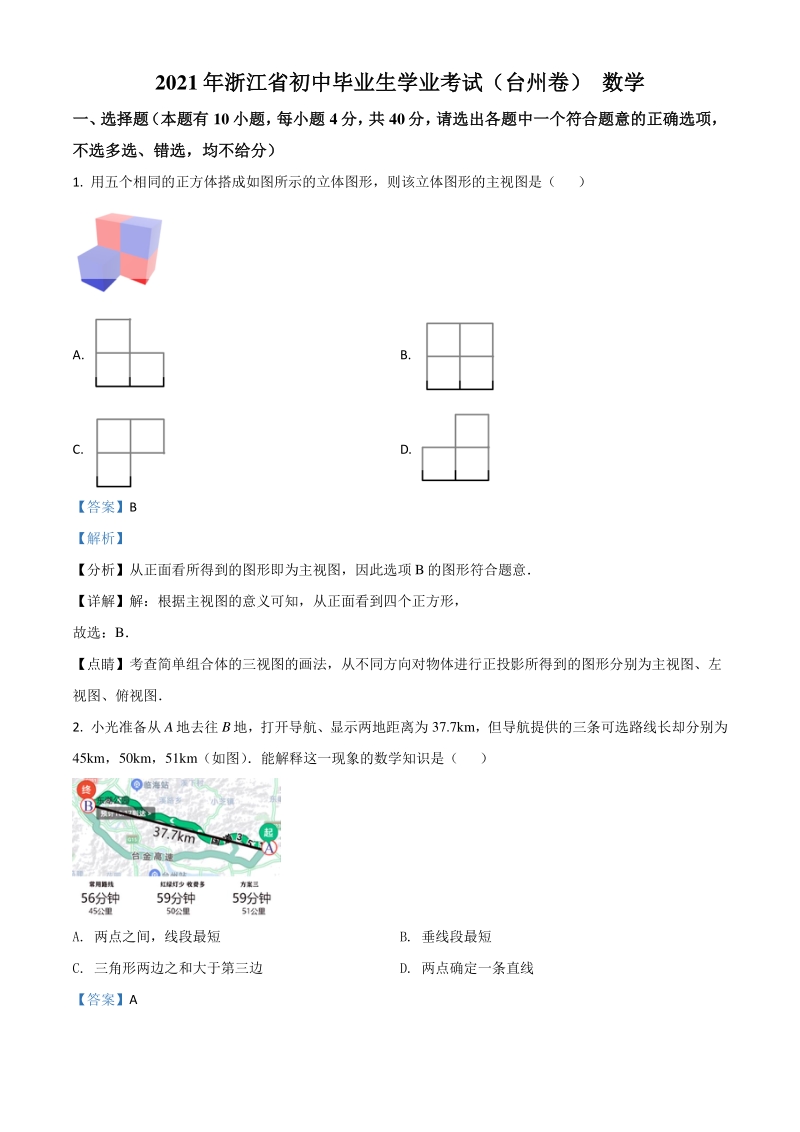
1、 2021 年浙江省初中毕业生学业考试（台州卷）年浙江省初中毕业生学业考试（台州卷） 数学数学 一、 选择题 （本题有一、 选择题 （本题有 10 小题， 每小题小题， 每小题 4 分， 共分， 共 40 分， 请选出各题中一个符合题意的正确选项，分， 请选出各题中一个符合题意的正确选项， 不选多选、错选，均不给分）不选多选、错选，均不给分） 1. 用五个相同的正方体搭成如图所示的立体图形，则该立体图形的主视图是（ ） A. B. C. D. 【答案】B 【解析】 【分析】从正面看所得到的图形即为主视图，因此选项 B的图形符合题意 【详解】解：根据主视图的意义可知，从正面看到四个正方形， 故选
2、：B 【点睛】考查简单组合体的三视图的画法，从不同方向对物体进行正投影所得到的图形分别为主视图、左 视图、俯视图 2. 小光准备从 A地去往 B地，打开导航、显示两地距离为 37.7km，但导航提供的三条可选路线长却分别为 45km，50km，51km（如图） 能解释这一现象的数学知识是（ ） A. 两点之间，线段最短 B. 垂线段最短 C. 三角形两边之和大于第三边 D. 两点确定一条直线 【答案】A 【解析】 【分析】根据线段的性质即可求解 【详解】解：两地距离显示的是两点之间的线段，因为两点之间线段最短，所以导航的实际可选路线都比 两地距离要长， 故选：A 【点睛】本题考查线段的性质，掌
3、握两点之间线段最短是解题的关键 3. 大小在 2和5之间的整数有（ ） A. 0个 B. 1个 C. 2个 D. 3个 【答案】B 【解析】 【分析】先估算 2和5的值，即可求解 【详解】解：1 22 ，253， 在 2和5之间的整数只有 2，这一个数， 故选：B 【点睛】此题主要考查了无理数的估算能力，解决本题的关键是得到最接近无理数的两个有理数的值现 实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法 4. 下列运算中，正确的是（ ） A. a2aa3 B. （- -ab）2- -ab2 C. a5a2a3 D. a5a2a10 【答案】C 【解析】
4、 【分析】根据合并同类项、积的乘方、同底数幂相除、同底数幂相乘的法则分别计算即可 【详解】解：A 2 a与 a 不是同类项，不能合并，故该项错误； B 22 2 baab，故该项错误； C 523 aaa，该项正确； D 527 aaa，该项错误； 故选：C 【点睛】本题考查整式的运算，掌握合并同类项、积的乘方、同底数幂相除、同底数幂相乘的法则是解题 的关键 5. 关于 x的方程 x2- -4xm0有两个不相等的实数根，则 m 的取值范围是（ ） A. m2 B. m2 C. m4 D. m4 【答案】D 【解析】 【分析】根据方程 x2- -4xm0有两个不相等实数根，可得 2 44 10m
5、 ，进而即可求解 【详解】解：关于 x的方程 x2- -4xm0有两个不相等的实数根， 2 44 10m ，解得：m4， 故选 D 【点睛】 本题主要考查一元二次方程根的判别式， 熟练掌握 ax2+bxc0（a0）有两个不相等的实数根， 则判别式大于零，是解题的关键 6. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋，设货架上原有鸡蛋的质量 （单位：g）平均数和方差分别为x，s2，该顾客选购的鸡蛋的质量平均数和方差x1， 2 1 s，则下列结论一 定成立的是（ ） A. xx 1 B. xx 1 C. s2 2 1 s D. s2 2 1 s 【答案】C 【解析】 【分析
6、】根据平均数和方差的意义，即可得到答案 【详解】解：顾客从一批大小不一的鸡蛋中选购了部分大小均匀的鸡蛋， 2 1 ss2，x和x1的大小关系不明确， 故选 C 【点睛】本题主要考查平均数和方差的意义，掌握一组数据越稳定，方差越小，是解题的关键 7. 一把直尺与一块直角三角板按如图方式摆放，若147，则2（ ） A. 40 B. 43 C. 45 D. 47 【答案】B 【解析】 【分析】过三角板的直角顶点作直尺两边的平行线，根据平行线的性质即可求解 【详解】解：如图，过三角板的直角顶点作直尺两边的平行线， 直尺的两边互相平行， 3147 ， 490343 ， 2443 ， 故选：B 【点睛】本
7、题考查平行线的性质，掌握平行线的性质是解题的关键 8. 已知（ab）249，a2b225，则 ab（ ） A. 24 B. 48 C. 12 D. 26 【答案】C 【解析】 【分析】利用完全平方公式计算即可 【详解】解： 2 22 249ababab， 22 25ab ， 4925 12 2 ab ， 故选：C 【点睛】本题考查整体法求代数式的值，掌握完全平方公式是解题的关键 9. 将 x 克含糖 10%的糖水与 y 克含糖 30%的糖水混合，混合后的糖水含糖（ ） A. 20% B. + 100% 2 x y C. +3 100% 20 xy D. +3 100% 10 +10 xy xy
8、 【答案】D 【解析】 【分析】先求出两份糖水中糖的重量，再除以混合之后的糖水总重，即可求解 【详解】解：混合之后糖的含量： 10%30%3 100% 1010 xyxy xyxy ， 故选：D 【点睛】本题考查列代数式，理解题意是解题的关键 10. 如图，将长、宽分别为 12cm，3cm的长方形纸片分别沿 AB，AC折叠，点 M，N恰好重合于点 P若 60 ，则折叠后的图案（阴影部分）面积为（ ） A. （36 6 3 ）cm2 B. （36 12 3 ）cm2 C. 24 cm2 D. 36 cm2 【答案】A 【解析】 【分析】过点 C 作CFMN，过点 B 作BEMN，根据折叠的性质求
9、出60PAC， 30EABPAB，分别解直角三角形求出 AB 和 AC 的长度，即可求解 【详解】解：如图，过点 C作CFMN，过点 B作BEMN， ， 长方形纸片分别沿 AB，AC 折叠，点 M，N恰好重合于点 P， 60PAC， 30EABPAB， 90BAC，6cm sin BE AB EAB ，2 3cm sin CF AC ， 1 6 3 2 ABC SAB AC， 2 12 36 3366 3 cm ABC SSS 阴矩形 ， 故选：A 【点睛】本题考查折叠的性质、解直角三角形，掌握折叠的性质是解题的关键 二、填空题（本题有二、填空题（本题有 6 小题，每小题小题，每小题 5 分，
10、共分，共 30 分）分） 11. 因式分解：xy- -y2_ 【答案】y(x-y) 【解析】 【分析】根据提取公因式法，即可分解因式 【详解】解：原式= y(x-y)， 故答案是：y(x-y) 【点睛】本题主要考查分解因式，掌握提取公因式法分解因式，是解题的关键 12. 一个不透明布袋中有 2 个红球，1 个白球，这些球除颜色外无其他差别，从中随机模出一个小球，该小 球是红色概率为_ 【答案】 2 3 【解析】 【分析】直接利用概率公式即可求解 【详解】解： 2 3 P摸出红球， 故答案为： 2 3 【点睛】本题考查求概率，掌握概率公式是解题的关键 13. 如图，将线段 AB绕点 A 顺时针旋
11、转 30，得到线段 AC若 AB12，则点 B 经过的路径BC长度为 _ （结果保留 ） 【答案】2 【解析】 【分析】直接利用弧长公式即可求解 【详解】解： 3012 2 180 BC l ， 故答案为：2 【点睛】本题考查弧长公式，掌握弧长公式是解题的关键 14. 如图，点 E， F，G分别在正方形 ABCD的边 AB，BC，AD上，AFEG若 AB5，AEDG1，则 BF_ 【答案】 5 4 【解析】 【分析】先证明ABFGAE，得到 ABBF GAAE ，进而即可求解 【详解】在正方形 ABCD中，AFEG， AGE+GAM =90 ，FAB+GAM=90 ， FAB =AGE， 又A
12、BF=GAE=90， ABFGAE， ABBF GAAE ，即： 5 5 11 BF ， BF= 5 4 故答案是： 5 4 【点睛】本题主要考查正方形的性质，相似三角形的判定和性质，证明ABFGAE，是解题的关键 15. 如图，在ABC中，ACB90，ACBC分别以点 A，B为圆心，大于 1 2 AB 的长为半径画弧，两 弧交于 D， E两点， 直线 DE交 BC于点 F， 连接 AF 以点 A为圆心， AF为半径画弧， 交 BC延长线于点 H， 连接 AH若 BC3，则AFH 的周长为_ 【答案】6 【解析】 【分析】根据作图可得 DF垂直平分线段 AB，利用线段垂直平分线的性质可得AFB
13、F，再根据等腰三角 形的三线合一可得AFH的周长222AFAHFHAFCFBFCFBC，即可求解 详解】解：由作图可得 DF 垂直平分线段 AB， AFBF， 以点 A 为圆心，AF为半径画弧，交 BC延长线于点 H， AFAH， AFAHBF ACBH， CFCH， AFH的周长2226AFAHFHAFCFBFCFBC， 故答案为：6 【点睛】本题考查尺规作图线段垂直平分线、等腰三角形的判定与性质，掌握上述基本性质定理是解题 的关键 16. 以初速度 v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度 h（单位：m） 与小球的运动时间 t（单位：s）之间的关系式是 h
14、vt4.9t2，现将某弹性小球从地面竖直向上抛出，初速 度为 v1，经过时间 t1落回地面，运动过程中小球的最大高度为 h1（如图 1） ；小球落地后，竖直向上弹起， 初速度为 v2， 经过时间 t2落回地面， 运动过程中小球的最大高度为 h2（如图 2） 若 h12h2， 则 t1： t2_ 【答案】 2 【解析】 【分析】根据函数图像分别求出两个函数解析式，表示出 1 1 4.9 v t ， 2 1 1 19.6 v h ， 2 2 4.9 v t ， 2 2 2 19.6 v h ，结 合 h12h2，即可求解 【详解】解：由题意得，图 1 中的函数图像解析式为：hv1t4.9t2，令
15、h=0， 1 1 4.9 v t 或 1 0t （舍去） ， 22 11 1 44.919.6 vv h ， 图 2中的函数解析式为：hv2t4.9t2， 2 2 4.9 v t 或 2 0t （舍去） ， 22 22 2 44.919.6 vv h ， h12h2， 2 1 19.6 v =2 2 2 19.6 v ，即： 1 v= 22 v或 1 v=- 22 v（舍去） ， t1：t2= 1 4.9 v ： 2 4.9 v = 2， 故答案是： 2 【点睛】本题主要考查二次函数的实际应用，掌握二次函数的图像和性质，二次函数的顶点坐标公式，是 解题的关键 三、解答题（本题有三、解答题（本题
16、有 8 小题，第小题，第 17 20 题每题题每题 8 分，第分，第 21 题题 10 分，第分，第 22，23 题每题题每题 12 分，分， 第第 24 分分 14 分，共分，共 80 分）分） 17. 计算：|2|123 【答案】2+ 3 【解析】 【分析】先算绝对值，化简二次根式，再算加减法，即可求解 【详解】解：原式=22 33 =2+ 3 【点睛】本题主要考查二次根式的运算，熟练掌握二次根式的性质以及合并同类二次根式法则，是解题的 关键 18. 解方程组： 24 1 xy xy 【答案】 1 2 x y . 【解析】 【分析】观察方程组中同一未知数的系数特点：x 的系数存在倍数关系，
17、而 y的系数互为相反数，因此将两 方程相加，消去 y求出 x，再求出 y的值，可得到方程组的解. 【详解】解：+得：3x=3， 即 x=1， 把 x=1 代入得：y=2， 则方程组的解为 1 2 x y . 【点睛】此题考查解二元一次方程组，解题关键在于利用加减消元法. 19. 图 1 是放置在水平地面上的落地式话筒架实物图，图 2是其示意图支撑杆 AB 垂直于地 l，活动杆 CD 固定在支撑杆上的点 E 处，若AED48，BE110 cm，DE80 cm，求活动杆端点 D 离地面的高度 DF （结果精确到 1cm，参考数据：sin480.74， cos480.67， tan481. 11）
18、【答案】164cm 【解析】 【分析】过点 E 作EMDF，易得四边形 EBFM 是矩形，即110cmMFBE，再通过解直角三角形 可得cosDMDEEDM，即可求解 【详解】解：过点 E作EMDF， EMDF，ABBF，DFBF， 90EMFEBFMFB， 四边形 EBFM是矩形， 110cmMFBE， AED48， 48EDMAED， cos80 0.6753.6cmDMDEEDM， 164cmDFDMMF 【点睛】本题考查解直角三角形的实际应用，做出合适的辅助线构造直角三角形是解题的关键 20. 小华输液前发现瓶中药液共 250 毫升，输液器包装袋上标有“15滴/毫升”输液开始时，药液流
19、速为 75 滴/分钟小华感觉身体不适，输液 10分钟时调整了药液流速，输液 20 分钟时，瓶中的药液余量为 160 毫升 （1）求输液 10 分钟时瓶中的药液余量； （2）求小华从输液开始到结束所需的时间 【答案】（1） 输液 10分钟时瓶中的药液余量为 200毫升；（2） 小华从输液开始到结束所需的时间为 60 分钟 【解析】 【分析】 （1）先求出每分钟输液多少毫升，进而即可求解； （2）先求出输液 10 分钟时调整后的药液流速，进而即可求解 【详解】 （1）解：7515=5（毫升/分钟） ， 250-510=200（毫升） ， 答：输液 10分钟时瓶中的药液余量为 200 毫升； （2）
20、 （200-160）10=4（毫升/分钟） ， 1604+20=60（分钟） ， 答：小华从输液开始到结束所需的时间为 60 分钟 【点睛】本题主要考查有理数运算的实际应用，明确时间，流速，输液量三者之间的数量关系，是解题的 关键 21. 如图，在四边形 ABCD中，ABAD20，BCDC10 2 （1）求证：ABCADC； （2）当BCA45时，求BAD的度数 【答案】 （1）见详解； （2）60 【解析】 【分析】 （1）通过 SSS证明ABCADC，即可； （2）先证明 AC垂直平分 BD，从而得BOC是等腰直角三角形，求出 BO= 10，从而得 BD=20，ABD 是等边三角形，进而即
21、可求解 【详解】 （1）证明：在ABC 和ADC 中， ABAD BCDC ACAC ABCADC（SSS） ， （2）连接 BD，交 AC于点 O， ABCADC， AB=AD，BC=DC， AC垂直平分 BD，即：AOB=BOC=90， 又BCA45， BOC是等腰直角三角形， BO=BC 2=1022=10， BD=2BO=20， ABAD20， ABD是等边三角形， BAD=60 【点睛】本题主要考查全等三角形的判定和性质，等腰直角三角形的判定和性质，等边三角形的判定和性 质，掌握垂直平分线的判定定理，是解题的关键 22. 杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果
22、农造成损失为此，市农科所开 展了用防雨布保护杨梅果实的实验研究 在某杨梅果园随机选择 40 棵杨梅树， 其中 20棵加装防雨布 （甲组） ， 另外 20棵不加装防雨布（乙组） 在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨 梅颗数占树上原有杨梅颗数的百分比） ，绘制成如下统计图表（数据分组包含左端值不包含右端值） 甲组杨梅树落果率频数分布表 落果率 组中值 频数（棵） 0 x10% 5% 12 10%x20% 15% 4 20%x30% 25% 2 30%x40% 35% 1 40%x50% 45% 1 乙组杨梅树落果率频数分布直方图 （1）甲、乙两组分别有几棵杨梅树的落果率低
23、于 20%？ （2）请用落果率的中位数或平均数，评价市农科所“用防雨布保护杨梅果实”的实际效果； （3）若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据 【答案】 （1）甲、乙两组分别有 16 棵和 2 棵杨梅树的落果率低于 20%；（2）“用防雨布保护杨梅果实” 大大降低了杨梅树的落果率，理由见详解； （3）该果园的杨梅树全部加装这种防雨布，落果率可降低 21% 【解析】 【分析】 （1）根据频数直方图和频数统计表，直接求解即可； （2）分别求出甲乙两组杨梅树落果率的组中值的中位数，即可得到结论； （3）分别求出甲乙两组杨梅的落果率的平均数，即可得到答案 【详解】解：
24、（1）12+4=16（棵） ，1+1=2（棵） ， 答：甲、乙两组分别有 16棵和 2 棵杨梅树的落果率低于 20%； （2）甲组杨梅树落果率的组中值从小到大排列： 5%，5%，5%，5%，5%，5%，5%，5%，5%，5%，5%，5%，15%，15%，15%，15%，25%，25%，35 %，45%， 甲组杨梅树落果率的组中值的中位数为：5%， 乙组杨梅树落果率的组中值从小到大排列：5%，15%， 25%，25%，25%，35%，35%，35%，35%，35%，35%，35%，35%，35%，35%，45%，45%，45%，45 %，45%， 乙组杨梅树落果率的组中值的中位数为：35%， “
25、用防雨布保护杨梅果实”的落果率的中位数低于“不加装防雨布”的落果率的中位数， “用防雨布保护杨梅果实”大大降低了杨梅树的落果率； （3） （125%+415%+225%+135%+145%） 20=12.5%， （15%+115%+325%+1035%+545%） 20=33.5%， 33.5%-12.5%=21%， 答：该果园的杨梅树全部加装这种防雨布，落果率可降低 21% 【点睛】本题主要考查频数直方图和频数统计表，中位数和平均数，准确从统计图表中找出数据，求出中 位数和平均数，是解题的关键 23. 电子体重科读数直观又便于携带，为人们带来了方便某综合实践活动小组设计了简易电子体重秤：制
26、作一个装有踏板（踏板质量忽略不计）的可变电阻 R1， R1与踏板上人的质量 m 之间的函数关系式为 R1 kmb（其中 k，b 为常数，0m120） ，其图象如图 1所示；图 2的电路中，电源电压恒为 8伏，定值电 阻 R0 的阻值为 30 欧，接通开关，人站上踏板，电压表显示的读数为 U0 ，该读数可以换算为人的质量 m， 温馨提示： 导体两端的电压 U，导体的电阻 R，通过导体的电流 I，满足关系式 I U R ； 串联电路中电流处处相等，各电阻两端电压之和等于总电压 （1）求 k，b的值； （2）求 R1关于 U0的函数解析式； （3）用含 U0的代数式表示 m； （4）若电压表量程为
27、06伏，为保护电压表，请确定该电子体重秤可称的最大质量 【答案】 （1） 240 1 2 b k ； （2） 1 0 240 30R U ；I（3） 0 480 540m U ； （4）该电子体重秤可称的最大质量 为 460 千克 【解析】 【分析】 （1）根据待定系数法，即可求解； （2）根据“串联电路中电流处处相等，各电阻两端的电压之和等于总电压”，列出等式，进而即可求解； （3）由 R1 1 2 m240， 1 0 240 30R U ，即可得到答案； （4）把 0 6U 时，代入 0 480 540m U ，进而即可得到答案 【详解】解： （1）把（0，240） ， （120，0）代入
28、 R1kmb，得 240 0120 b kb ，解得： 240 1 2 b k ； （2） 00 1 8 30 UU R ， 1 0 240 30R U ； （3）由（1）可知： 240 1 2 b k ， R1 1 2 m240， 又 1 0 240 30R U ， 0 240 30 U = 1 2 m240，即： 0 480 540m U ； （4）电压表量程为 06伏， 当 0 6U 时， 480 540460 6 m 答：该电子体重秤可称的最大质量为 460 千克 【点睛】本题主要考查一次函数与反比例函数的实际应用，熟练掌握待定系数法，是解题的关键 24. 如图，BD是半径为 3的O的
29、一条弦，BD4 2，点 A是O上的一个动点（不与点 B，D 重合） ， 以 A，B，D 为顶点作平行四边形 ABCD （1）如图 2，若点 A是劣弧BD的中点 求证：平行四边形 ABCD是菱形； 求平行四边形 ABCD的面积 （2）若点 A运动到优弧BD上，且平行四边形 ABCD有一边与O相切 求 AB 的长； 直接写出平行四边形 ABCD 对角线所夹锐角的正切值 【答案】证明见解析；8 2； （2）AB 的长为 8 2 3 或4 2； 8 2 5 【解析】 【分析】 （1）利用等弧所对的弦相等可得ADAB，根据一组邻边相等的平行四边形是菱形可得证； 连接 AO，交 BD 于点 E，连接 OD
30、，根据垂径定理可得 2 2DEBE ，利用勾股定理求出 OE 的长，即 可求解； （2）分情况讨论当 CD与O相切时、当 BC 与O相切时，利用垂径定理即可求解；根据等面积法 求出 AH 的长度，利用勾股定理求出 DH的长度，根据正切的定义即可求解 【详解】解： （1）点 A 是劣弧BD的中点， AD AB ， ADAB， 四边形 ABCD是平行四边形， 平行四边形 ABCD是菱形； 连接 AO，交 BD 于点 E，连接 OD， ， 点 A是劣弧BD的中点，OA为半径， OABD，OA 平分 BD， 2 2DEBE ， 平行四边形 ABCD是菱形， E为两对角线的交点， 在RtODE中， 22
31、 1OEODDE , 2AE ， 1 28 2 2 ABCD SBD AE； （2）如图，当 CD与O相切时，连接 DO并延长，交 AB于点 F， CD与O相切， DFCD， 2ABBF， 四边形 ABCD是平行四边形， /AB CD， DFAB， 在RtBDF中， 2 222 323BFBDDFOF， 在RtBOF中， 2222 9BFBOOFOF， 2 2 3239OFOF，解得 7 3 OF ， 4 2 3 BF ， 8 22 3 ABBF； 如图，当 BC 与O相切时，连接 BO 并延长，交 AD于点 G， 同理可得 4 2 3 AGDG， 7 3 OG ， 所以 22 4 2ABBGAG , 综上所述，AB长为 8 2 3 或4 2； 过点 A 作AHBD， ， 由（2）得： 8716 4 2,2,3, 333 BDADBG 根据等面积法可得 11 22 BD AHAD BG， 解得 32 9 AH ， 在在Rt ADH中， 22 8 2 9 DHADAH， 810 2 222 99 HI ， 8 tan2 5 AH AIH HI 【点睛】本题考查垂径定理、平行四边形的判定与性质、解直角三角形等内容，掌握分类讨论的思想是解 题的关键
