 2021年四川省乐山市中考数学试卷(含答案详解)
2021年四川省乐山市中考数学试卷(含答案详解)
《2021年四川省乐山市中考数学试卷(含答案详解)》由会员分享,可在线阅读,更多相关《2021年四川省乐山市中考数学试卷(含答案详解)(27页珍藏版)》请在七七文库上搜索。
1、2021 年四川省乐山市中考数学试卷年四川省乐山市中考数学试卷 一、选择题:本大题共一、选择题:本大题共 10 个小题,每小题个小题,每小题 3 分,共分,共 30 分分. 1 (3 分)如果规定收入为正,那么支出为负,收入 2 元记作+2,支出 5 元记作( ) A5 元 B5 元 C3 元 D7 元 2 (3 分)在一次心理健康教育活动中,张老师随机抽取了 40 名学生进行了心理健康测试,并将测试结果 按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ) 类型 健康 亚健康 不健康 数据(人) 32 7 1 A32 B7 C D 3 (3 分)某种商品 m 千克的
2、售价为 n 元,那么这种商品 8 千克的售价为( ) A(元) B(元) C(元) D(元) 4 (3 分)如图,已知直线 l1、l2、l3两两相交,且 l1l3,若 50,则 的度数为( ) A120 B130 C140 D150 5 (3 分)如图,已知直线 l1:y2x+4 与坐标轴分别交于 A、B 两点,那么过原点 O 且将AOB 的面积 平分的直线 l2的解析式为( ) Ayx Byx Cyx Dy2x 6(3 分) 如图是由 4 个相同的小正方体堆成的物体, 将它在水平面内顺时针旋转 90后, 其主视图是 ( ) A B C D 7 (3 分)七巧板起源于我国先秦时期,古算书周髀算
3、经中有关于正方形的分割术,经历代演变而成七 巧板,如图 1 所示.19 世纪传到国外,被称为“唐图” (意为“来自中国的拼图” ) ,图 2 是由边长为 4 的 正方形分割制作的七巧板拼摆而成的 “叶问蹬”图, 则图中抬起的 “腿” (即阴影部分) 的面积为 ( ) A3 B C2 D 8 (3 分)如图,已知点 P 是菱形 ABCD 的对角线 AC 延长线上一点,过点 P 分别作 AD、DC 延长线的垂 线,垂足分别为点 E、F若ABC120,AB2,则 PEPF 的值为( ) A B C2 D 9 (3 分)如图,已知 OA6,OB8,BC2,P 与 OB、AB 均相切,点 P 是线段 A
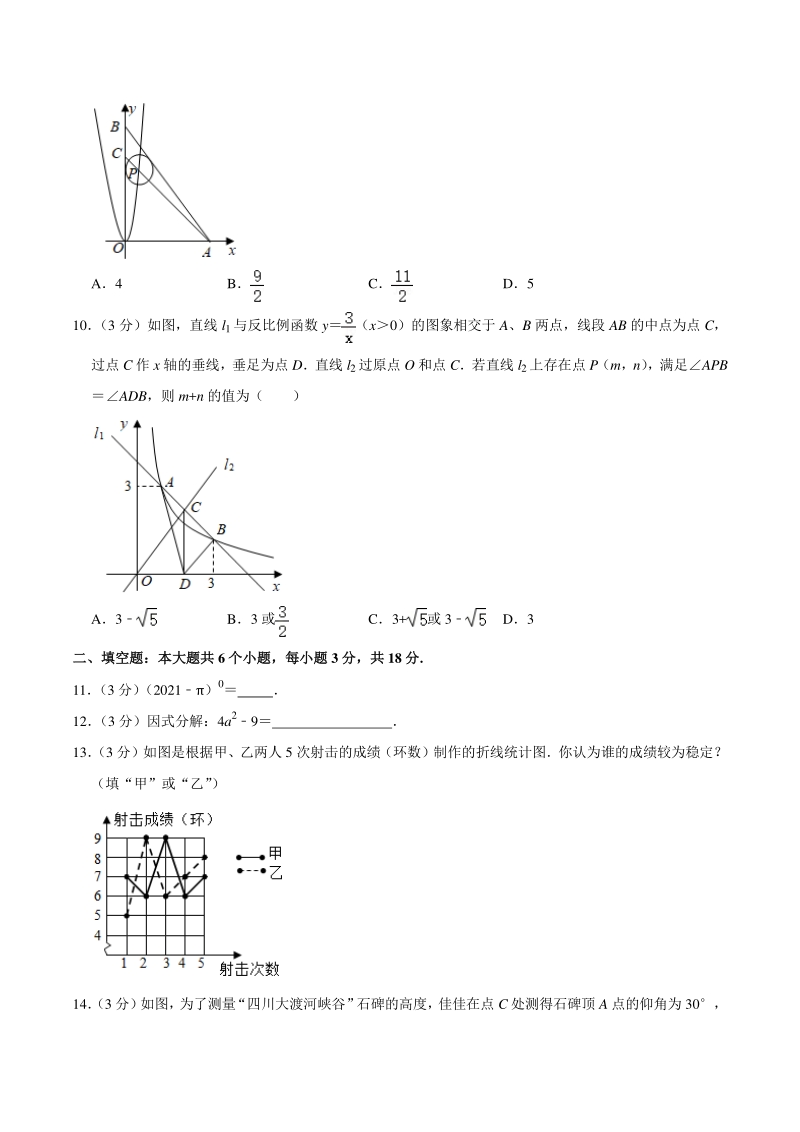
4、C 与抛物线 yax2 的交点,则 a 的值为( ) A4 B C D5 10 (3 分)如图,直线 l1与反比例函数 y(x0)的图象相交于 A、B 两点,线段 AB 的中点为点 C, 过点 C 作 x 轴的垂线,垂足为点 D直线 l2过原点 O 和点 C若直线 l2上存在点 P(m,n) ,满足APB ADB,则 m+n 的值为( ) A3 B3 或 C3+或 3 D3 二、填空题:本大题共二、填空题:本大题共 6 个小题,每小题个小题,每小题 3 分,共分,共 18 分分. 11 (3 分) (2021)0 12 (3 分)因式分解:4a29 13 (3 分)如图是根据甲、乙两人 5 次
5、射击的成绩(环数)制作的折线统计图你认为谁的成绩较为稳定? (填“甲”或“乙” ) 14 (3 分) 如图, 为了测量 “四川大渡河峡谷” 石碑的高度, 佳佳在点 C 处测得石碑顶 A 点的仰角为 30, 她朝石碑前行 5 米到达点 D 处,又测得石碑顶 A 点的仰角为 60,那么石碑的高度 AB 的长 米 (结果保留根号) 15 (3 分)在 RtABC 中,C90,有一个锐角为 60,AB4若点 P 在直线 AB 上(不与点 A,B 重合) ,且PCB30,则 CP 的长为 16 (3 分)如图,已知点 A(4,3) ,点 B 为直线 y2 上的一动点,点 C(0,n) ,2n3,ACBC
6、 于点 C,连接 AB若直线 AB 与 x 正半轴所夹的锐角为 ,那么当 sin 的值最大时,n 的值 为 三、本大题共三、本大题共 3 个小题,每小题个小题,每小题 9 分,共分,共 27 分分. 17 (9 分)当 x 取何正整数值时,代数式与的值的差大于 1 18 (9 分)如图已知 ABDC,AD,AC 与 DB 相交于点 O,求证:OBCOCB 19 (9 分)已知,求 A、B 的值 四、本大题共四、本大题共 3 个小题,每小题个小题,每小题 10 分,共分,共 30 分分. 20 (10 分)已知关于 x 的一元二次方程 x2+xm0 (1)若方程有两个不相等的实数根,求 m 的取
7、值范围; (2)二次函数 yx2+xm 的部分图象如图所示,求一元二次方程 x2+xm0 的解 21 (10 分)某中学全校师生听取了“禁毒”宣传报告后,对禁毒人员肃然起敬学校德育处随后决定在全 校 1000 名学生中开展“我为禁毒献爱心”的捐款活动张老师在周五随机调查了部分学生随身携带零花 钱的情况,并将收集的数据进行整理,绘制了如图所示的条形统计图 (1)求这组数据的平均数和众数; (2)经调查,当学生身上的零花钱多于 15 元时,都愿捐出零花钱的 20%,其余学生不参加捐款请你 估计周五这一天该校可能收到学生自愿捐款多少元? (3)捐款最多的两人将和另一个学校选出的两人组成一个“禁毒”知
8、识宣讲小组,若从 4 人中随机指定 两人担任正、副组长,求这两人来自不同学校的概率 22 (10 分)如图,直线 l 分别交 x 轴、y 轴于 A、B 两点,交反比例函数 y(k0)的图象于 P、Q 两 点若 AB2BP,且AOB 的面积为 4 (1)求 k 的值; (2)当点 P 的横坐标为1 时,求POQ 的面积 五、本大题共五、本大题共 2 个小题,每小题个小题,每小题 10 分,共分,共 20 分分. 23(10 分) 通过实验研究发现: 初中生在数学课上听课注意力指标随上课时间的变化而变化, 上课开始时, 学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散学生注意力指标
9、 y 随时间 x (分钟)变化的函数图象如图所示,当 0 x10 和 10 x20 时,图象是线段;当 20 x45 时,图象 是反比例函数的一部分 (1)求点 A 对应的指标值; (2)张老师在一节课上讲解一道数学综合题需要 17 分钟,他能否经过适当的安排,使学生在听这道综 合题的讲解时,注意力指标都不低于 36?请说明理由 24 (10 分)如图,已知点 C 是以 AB 为直径的半圆上一点,D 是 AB 延长线上一点,过点 D 作 BD 的垂线 交 AC 的延长线于点 E,连结 CD,且 CDED (1)求证:CD 是O 的切线; (2)若 tanDCE2,BD1,求O 的半径 六、本大
10、题共六、本大题共 2 个小题,第个小题,第 25 题题 12 分,第分,第 26 题题 13 分,共分,共 25 分分. 25 (12 分)在等腰ABC 中,ABAC,点 D 是 BC 边上一点(不与点 B、C 重合) ,连结 AD (1)如图 1,若C60,点 D 关于直线 AB 的对称点为点 E,连结 AE,DE,则BDE ; (2)若C60,将线段 AD 绕点 A 顺时针旋转 60得到线段 AE,连结 BE 在图 2 中补全图形; 探究 CD 与 BE 的数量关系,并证明; (3)如图 3,若k,且ADEC试探究 BE、BD、AC 之间满足的数量关系,并证明 26 (13 分)已知二次函
11、数 yax2+bx+c 的图象开口向上,且经过点 A(0,) ,B(2,) (1)求 b 的值(用含 a 的代数式表示) ; (2)若二次函数 yax2+bx+c 在 1x3 时,y 的最大值为 1,求 a 的值; (3)将线段 AB 向右平移 2 个单位得到线段 AB若线段 AB与抛物线 yax2+bx+c+4a1 仅有 一个交点,求 a 的取值范围 2021 年四川省乐山市中考数学试卷年四川省乐山市中考数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题:本大题共一、选择题:本大题共 10 个小题,每小题个小题,每小题 3 分,共分,共 30 分分. 1 (3 分)如果规定收入为正,
12、那么支出为负,收入 2 元记作+2,支出 5 元记作( ) A5 元 B5 元 C3 元 D7 元 【解答】解:如果规定收入为正,那么支出为负,收入 2 元记作+2,支出 5 元记作5 元 故选:B 2 (3 分)在一次心理健康教育活动中,张老师随机抽取了 40 名学生进行了心理健康测试,并将测试结果 按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ) 类型 健康 亚健康 不健康 数据(人) 32 7 1 A32 B7 C D 【解答】解:抽取了 40 名学生进行了心理健康测试,测试结果为“健康”的有 32 人, 测试结果为“健康”的频率是: 故选:D 3 (3 分
13、)某种商品 m 千克的售价为 n 元,那么这种商品 8 千克的售价为( ) A(元) B(元) C(元) D(元) 【解答】解:根据题意,得:8(元) , 故选:A 4 (3 分)如图,已知直线 l1、l2、l3两两相交,且 l1l3,若 50,则 的度数为( ) A120 B130 C140 D150 【解答】解:如图,根据对顶角相等得:150, l1l3, 290 是三角形的外角, 1+250+90140, 故选:C 5 (3 分)如图,已知直线 l1:y2x+4 与坐标轴分别交于 A、B 两点,那么过原点 O 且将AOB 的面积 平分的直线 l2的解析式为( ) Ayx Byx Cyx
14、Dy2x 【解答】解:如图,当 y0,2x+40,解得 x2,则 A(2,0) ; 当 x0,y2x+44,则 B(0,4) , AB 的中点坐标为(1,2) , 直线 l2把AOB 面积平分 以 l2经过 AB 的中点; 直线 l2过 AB 的中点, 设直线 l2的解析式为 ykx, 把(1,2)代入得 2k,解得 k2, l2的解析式为 y2x, 故选:D 6(3 分) 如图是由 4 个相同的小正方体堆成的物体, 将它在水平面内顺时针旋转 90后, 其主视图是 ( ) A B C D 【解答】解:顺时针旋转 90后,从正面看第一列有一层,第二列有两层, 故选:C 7 (3 分)七巧板起源于
15、我国先秦时期,古算书周髀算经中有关于正方形的分割术,经历代演变而成七 巧板,如图 1 所示.19 世纪传到国外,被称为“唐图” (意为“来自中国的拼图” ) ,图 2 是由边长为 4 的 正方形分割制作的七巧板拼摆而成的 “叶问蹬”图, 则图中抬起的 “腿” (即阴影部分) 的面积为 ( ) A3 B C2 D 【解答】解:由题意,阴影部分的平行四边形的面积212, 阴影部分的三角形的面积211, 阴影部分的面积2+13, 故选:A 8 (3 分)如图,已知点 P 是菱形 ABCD 的对角线 AC 延长线上一点,过点 P 分别作 AD、DC 延长线的垂 线,垂足分别为点 E、F若ABC120,
16、AB2,则 PEPF 的值为( ) A B C2 D 【解答】解:设 AC 交 BD 于 O,如图: 菱形 ABCD,ABC120,AB2, BADBCD60,DACDCA30,ADAB2,BDAC, RtAOD 中,ODAD1,OA, AC2OA2, RtAPE 中,DAC30,PEAP, RtCPF 中,PCFDCA30,PFCP, PEPFAPCP(APCP)AC, PEPF, 故选:B 9 (3 分)如图,已知 OA6,OB8,BC2,P 与 OB、AB 均相切,点 P 是线段 AC 与抛物线 yax2 的交点,则 a 的值为( ) A4 B C D5 【解答】解:设P 与 OB、AB
17、 分别相切于点 M、N,连接 PM、PN, 设圆的半径为 x,则 PNPMx, 由题意知,OCAO6,则直线 BA 与 y 轴的夹角为 45,则 CMMPx, 由点 A、C 的坐标得,直线 AC 的表达式为 yx+6, 则点 P 的坐标为(x,x+6) , 由点 P、A 的坐标得,PA(6x) , 则 AN, P 与 OB、AB 分别相切于点 M、N,故 BNBMBC+CM2+x, 在 RtABO 中,OA6,OB8,则 AB10BN+AN, 即 10+2+x,解得 x1, 故点 P 的坐标为(1,5) , 将点 P 的坐标代入 yax2得 5a, 故选:D 10 (3 分)如图,直线 l1与


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 四川省 乐山市 中考 数学试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 数学试卷
- 四川中考真题数学
- 2021年淮安市中考数学真题试卷含答案详解
- 2021年四川省乐山市中考物理试题含答案
- 四川省乐山市新桥中学
- 四川省乐山市延风中学
- 2019年四川省乐山市中考数学试题含答案解析
- 2021年四川省乐山市中考语文试卷含答案
- 2017年四川省乐山市中考数学试卷含答案解析
- 2019年四川省乐山市中考数学试卷含答案解析2
- 2021年四川省乐山市中考历史模拟试卷一含答案
- 2021年四川省乐山市中考语文试题word版含答案
- 2019年四川省乐山市中考化学试卷含详细答案
- 2021年四川省乐山市中考历史模拟试卷二含答案
- 2020年四川省乐山市中考数学试卷含详细解答
- 2019年四川省乐山市中考地理试卷含答案
- 2021年四川省乐山市中考数学全真模拟试卷一含答案
- 2021年四川省乐山市中考数学试卷含答案详解
- 2018年四川省乐山市中考英语试卷含答案解析
- 2021年四川省乐山市中考化学全真模拟试卷2含答案



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-186283.html