1、 南通市南通市 2021 年中考数学考前押题卷年中考数学考前押题卷 一、选择题（本大题共一、选择题（本大题共 10 小题，每小题小题，每小题 3 分，共分，共 30 分分.在每小题给出的四个选项中，只有一项是符合题在每小题给出的四个选项中，只有一项是符合题 目要求的目要求的) 1(本题 3 分)下列计算正确的是 （ ） A （3）（5）=8 B （3）（5）=8 C （3）3=9 D32=9 2(本题 3 分)下列计算正确的是（ ） Aa2a3a5 B （-2x2y）3-6x6y3 C （a-b） （-a-b）a2-b2 D2x2（- 1 3 xy）- 2 3 x3y 3(本题 3 分)下列函
2、数中，自变量取值范围错误的是（ ） A 11 () 212 yx x B1(1)yx x C 2 1(yxx为任意实数） D 1 (1) 1 yx x 4(本题 3 分)如图所示的几何体的左视图是（ ） A B C D 5 (本题 3 分)对某班最近一次数学测试成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘 制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为 A 等(80 分以上,不含 80 分) 的百分率为( ) A24% B40% C42% D50% 6(本题 3 分)德国数学家高斯在大学二年级时得出了正十七边形是尺规作图法，并给出了可用尺规作图的
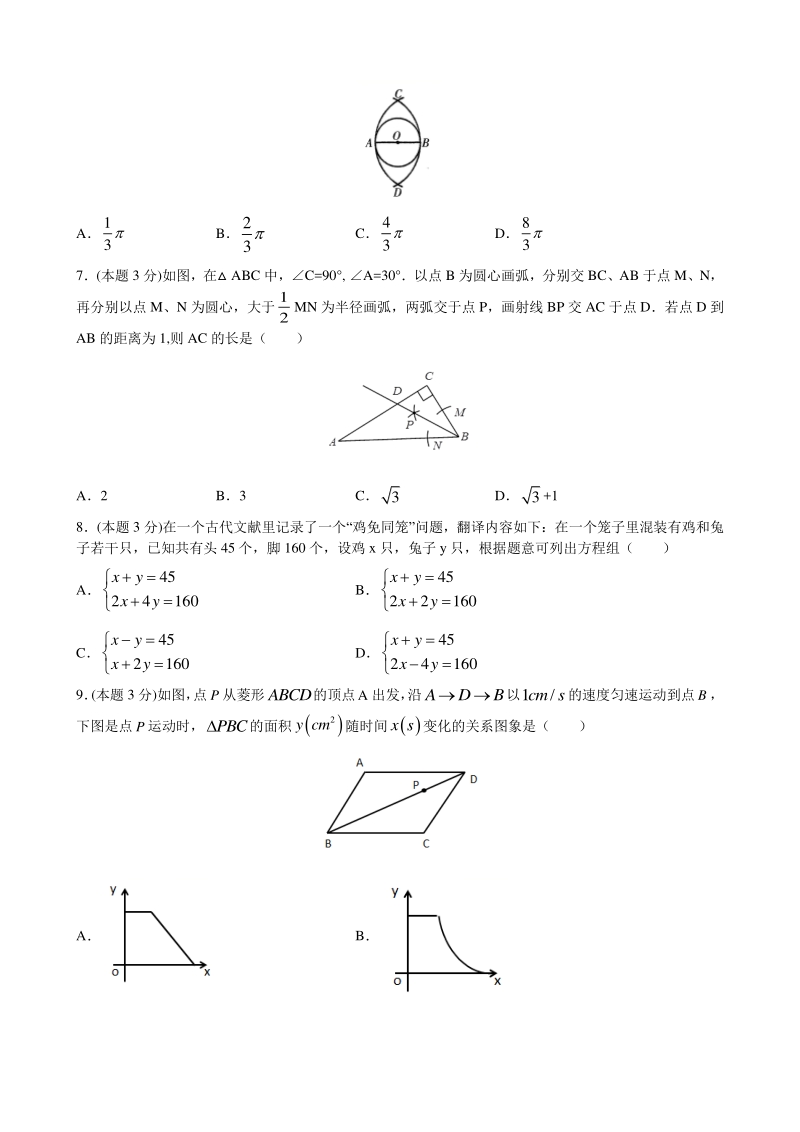
3、正多边形的条件.下面是高斯正十七边形作法的一部分： “如图， 已知 AB 是圆 O 的直径，分别以 A， B 为圆心、 AB 长为半径作弧，两弧交于点 C， D 两点”.若 AB 长为 2， 则图中弧 CAD 的长为 （ ） A 1 3 B 2 3 C 4 3 D 8 3 7(本题 3 分)如图，在 ABC 中，C=90 , A=30 以点 B 为圆心画弧，分别交 BC、AB 于点 M、N， 再分别以点 M、N 为圆心，大于 1 2 MN 为半径画弧，两弧交于点 P，画射线 BP 交 AC 于点 D若点 D 到 AB 的距离为 1,则 AC 的长是（ ） A2 B3 C 3 D3+1 8(本题
4、 3 分)在一个古代文献里记录了一个“鸡免同笼”问题，翻译内容如下：在一个笼子里混装有鸡和兔 子若干只，已知共有头 45 个，脚 160 个，设鸡 x 只，兔子 y 只，根据题意可列出方程组（ ） A 45 24160 xy xy B 45 22160 xy xy C 45 2160 xy xy D 45 24160 xy xy 9 (本题 3 分)如图， 点P从菱形ABCD的顶点A出发， 沿ADB以1/cm s的速度匀速运动到点B， 下图是点P运动时，PBC的面积 2 y cm 随时间 x s变化的关系图象是（ ） A B C D 10(本题 3 分)如图面积为 24 的四边形ABCD内接于
5、圆O，对角线AC与BD相交于点E，AECE， 2ABAE ，且8BD，则圆O的半径是（ ） A5 B3 5 C4 2 D 25 6 二、填空题（本大题共二、填空题（本大题共 8 小题，第小题，第 1112 题每小题题每小题 3 分，第分，第 1318 题每小题题每小题 4 分，共分，共 30 分分) 11(本题 3 分)（0.09）2的平方根是_ 12(本题 3 分)地球半径大约是 6370 千米，用科学记数法表示为_米. 13(本题 4 分)如图，已知 ABCD，EFCD，ABC45 ，CEF150 ，则BCE 等于_度 14(本题 4 分)当 m+n=3 时,式子 m2+2mn+n2的值为
6、_. 15(本题 4 分)若正六边形的边长为 3，则其面积为_ 16(本题 4 分)今年春节期间，为了进一步做好新型冠状病毒感染的肺炎疫情防控工作，防止新型肺炎外 传，切断传播途径.北海市区各入口一些主要路段均设立了检测点，对出入人员进行登记和体温检测.如图 为一关口的警示牌，已知立杆AB高度是2m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是 60 和 45 ，则警示牌BC的高度为_m.（结果保留根号） 17(本题 4 分)如图，直线 3 3 3 yx 交 x 轴于点 A，交 y 轴于点 B，点 P 是 x 轴上一动点，以点 P 为 圆心，以 1 个单位长度为半径作P，当P 与直线 A
7、B 相切时，点 P 的横坐标是_ 18(本题 4 分)如图，已知一次函数 y1k1xb 的图象与 x 轴、y 轴分别交于 A、B 两点，与反比例函数 y2 2 k x 的图象分别交于 C、D 两点，点 D 的坐标为(2，3)，点 B 是线段 AD 的中点则不等式 k1xb 2 k x 0 的解集是_. 三、解答题（本大三、解答题（本大题共题共 8 小题，共小题，共 90 分解答时应写出必要的计算过程、推演步骤或文字说明分解答时应写出必要的计算过程、推演步骤或文字说明) 19(本题 10 分)先化简，再求值： 22 22 2 244 xyxy xyxxyy ，其中 22x ，y=2 2-1 20
8、(本题 11 分)佳佳文具店购进 A， B 两种款式的笔袋， 其中 A 种笔袋的单价比 B 种袋的单价低 10% 已 知店主购进 A 种笔袋用了 810 元，购进 B 种笔袋用了 600 元，且所购进的 A 种笔袋的数量比 B 种笔袋多 20 个请问：文具店购进 A，B 两种款式的笔袋各多少个？ 21(本题 12 分)已知直线y = kx + 2(k 0)经过点(1,3) （1）求k的值； （2）求此直线与x轴、y轴围成的三角形面积 22(本题 10 分)学校选派 25 名志愿者准备参加社会服务工作，其中男生 15 人，女生 10 人， (1)若从这 25 人中通过抽签选取一人作为联络员，求选
9、到女生的概率 (2)一项工作只在甲、乙两人中选一人，他俩以游戏方式决定谁参加规则如下：将 4 张点数分别为 2，3， 4， 5 的扑克牌洗匀后， 背面朝上放于桌面， 从中任取 2 张若点数之和为合数， 则甲得 1 分； 否则乙得 1 分 谁 先满 10 分谁参加这个游戏公平吗?请说明理由 23(本题 9 分)“新型冠状病毒肺炎”疫情牵动着亿万国人的心，为进一步加强疫情防控工作，某学校利用 网络平台进行疫情防控知识测试 小青从全体学生中随机抽取部分同学的分数 （得分取正整数， 满分为 100 分）进行统计，以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图，请根据图表， 回答下列问
10、题： 组别 分组 频数 频率 1 5060 x 9 0.18 2 6070 x m b 3 7080 x 21 0.42 4 8090 x a 0.06 5 90100 x 2 n （1）根据上表填空：a ，b ，m ； （2）若小青的测试成绩是抽取的同学成绩的中位数，则小青的测试成绩在什么范围内？ （3）若规定：得分在 90 x100 的为“优秀”，若小青所在学校共有 600 名学生，从本次比赛选取得分为“优 秀”的学生参加决赛，请问共有多少名学生被选拔参加决赛？ 24(本题 12 分)如图，在 ABC 中，AB=AC，AD 是 BC 边上的中线，E 是 AB 上一点，且 AE=DE （1）
11、求证：DE/AC （2）若 BE=5，BC=12，求 AED 的周长 25(本题 13 分)如图，抛物线 yx22x 的顶点为 A，与 x 轴交于 B、C 两点（点 B 在点 C 的左侧） （1）请求出 A、B、C 三点的坐标； （2）平移抛物线，记平移后的抛物线的顶点为 D，与 y 轴交于点 E，F 为平面内一点，若以 A、D、E、F 为顶点的四边形是正方形，且平移后的抛物线的对称轴在 y 轴右侧，请求出满足条件的平移后抛物线的表 达式 26(本题 13 分)在ABC中，BDAC于点D，点为射线BD上任一点（点B除外）连接AP，将线 段PA绕点顺时针方向旋转，ABC，得到PE，连接CE （1
12、） （观察发现）如图 1，当BABC，且60ABC时，BP 与CE的数量关系是_，BC 与CE的位置关系是_ （2） （猜想证明）如图 2，当BABC，且90ABC时， （1）中的结论是否成立？若成立，请予以证 明；若不成立，请说明理由 （请选择图 2，图 3 中的一种情况予以证明或说理） （3） （拓展探究）在（2）的条件下，若8AB， 5 2AP ，请直接写出CE的长 参考答案参考答案 1D 【解析】解：A、 （-3）-（-5）=（-3）+（+5）=2，故本选项错误； B、 （-3）+（-5）=-（3+5）=-8，故本选项错误； C、 （-3）3=（-3） （-3） （-3）=-27，故本
13、选项错误； D、-32=-3 3=-9，正确 故选 D 2D 【解析】a2与 a3不是同类项 a2与 a3不能合并 选项 A 不合题意； 3 263 28x yx y 选项 B 不合题意； （a-b） （-a-b）b2-a2 选项 C 不合题意； 2x2（- 1 3 xy）- 2 3 x3y 选项 D 符合题意； 故选：D 3D 【解析】解： 1 21 y x 的自变量的取值范围为 2x-10，即 1 2 x ，故选项 A 正确； 1yx的自变量的取值范围为 1-x0，即1x，故选项 B 正确； 2 1yx的自变量的取值范围为x为任意实数，故选项 C 正确； 1 1 y x 的自变量的取值范围
14、为 x-10，即1x 故选项 D 不正确； 故选：D 4A 【解析】该几何体的左视图有两层，第一层有 1 个正方形，第二层有 1 个正方形， 故选：A 5C 【解析】5+9+15+14+7=50， （14+7） 50=42%. 故选 C. 6C 【解析】解：连接 AC、BC、DA、DB，如图， 由作法得 BC=BA=AC=BD=AD， ACB 和 ADB 都是等边三角形， ABC=ABD=60 ， 图中弧 CAD 的长=120 2 180 = 4 3 故选 C 7B 【解析】解：如图， 过点 D 作 DEAB 于 E，则 DE=1， C=90 , A=30 ， 60ABC 由尺规作图，知 PB
15、 是ABC的平分线， 1 30 2 ABDABC， AABD ， ADDB， 2ABEB， 在RtDBE中， 1 3 t a n 3 03 3 DE EB 2 3AB， 在Rt ABC中， 3 cos302 33 2 ACAB , 故选：B 8A 【解析】解：设鸡 x 只，兔子 y 只，共有头 45 个， 故依据题意可得： 45 24160 xy xy 故选：A 9A 【解析】当点 P 在 AD 上时，此时 BC 是定值，BC 边的高是定值，则 PBC 的面积 y 是定值； 当点 P 在 BD 上时，此时 BC 是定值，BC 边的高与运动时间 x 成正比例的关系，则 PBC 的面积 y 与 运
16、动时间 x 是一次函数，并且 PBC 的面积 y 与运动时间 x 之间是减函数，y0 所以只有 A 符合要求 故选：A 10D 【解析】解：连接 OA、OB，OA 交 BD 于 F AECE， 2ABAE ， 1 2 AEAC，2 AB AE 2 2 2 ABAEAC 2 AC AB ABAC AEAB BAC=EAB BACEAB ACB=ABE ACB=ADB ADB=AEB AD=AB 点 A 在 BD 的中垂线上 点 O 也在 BD 的中垂线上 OA 垂直平分 BD AFB=OFB=90 ，BF= 1 4 2 BD 点 E 是 CA 的中点 S ADE= 1 2 S ADC，S BAE
17、= 1 2 S BAC S ADB= S ADES BAE= 1 2 S ADC 1 2 S BAC= 1 2 （S ADCS BAC）= 1 2 S四边形ABCD=12 即 1 2 BD AF=12 解得：AF=3 设 OA=OB=r，则 OF=OAAF=r3 在 Rt OFB 中，OF2BF2=OB2 （r3）242=r2 解得： 25 6 r 故选 D 110.09 【解析】 22 ( 0.09)0.09， 2 0.09的平方根是0.09， 故答案为：0.09 126.37 106 【解析】解：将 6370 千米用科学记数法表示为 6.37 106米 故答案为 6.37 106 1315
18、. 【解析】解：ABCD，ABC45， BCDABC45， EFCD， ECD+CEF180， CEF150， ECD180CEF18015030， BCEBCDECD 453015， BCE 的度数为 15 故答案为：15 149 【解析】将代数式化为完全平方公式的形式，代入即可得出答案：m2+2mn+n2=（m+n）2=9 15 27 3 2 【解析】解：此多边形为正六边形，如图： AOB 360 6 60 ； OAOB， OAB 是等边三角形， OAAB3， OGOAcos303 3 2 3 3 2 ， S OAB 1 2 AB OG 1 2 333 2 9 3 4 ， S六边形6S O
19、AB693 4 27 3 2 故答案为： 27 3 2 ； 16 2 32 【解析】解：在Rt ADB中，45BDA，2AB ， 2DA 在Rt ADC中，60CDA， tan60 AC AD ， tan602 3CADA ， 2 32BCCABA （米) 答：路况显示牌BC的高度是 2 32 米 173 323 32或 【解析】直线 3 3 3 yx 交 x 轴于点 A，交 y 轴于点 B， 令 x=0，得 y=-3，令 y=0，得 x=3 3， A（3 3，0） ，B（0-3） ， OA=3 3，OB=3， AB=6， 设P 与直线 AB 相切于 D，连接 PD， 则 PDAB，PD=1，
20、 ADP=AOB=90 ，PAD=BAO， APDABO， PDAP OBAB ， 1 36 AP ， AP=2， OP=3 3-2 或 OP=33+2， P（3 3-2，0）或 P（33+2，0） ， 故答案为：3 323 32或 18x4 或 0x2 【解析】点 D（2，3）在反比例函数 y2= 2 k x 的图象上，k2=2 （3）=6，y2= 6 x ； 作 DEx 轴于 ED（2，3） ，点 B 是线段 AD 的中点，A（2，0） A（2，0） ，D（2，3） 在 y1=k1x+b 的图象上， 1 1 20 23 kb kb ， 解得： k1= 3 4 ， b= 3 2 ， y1 =
21、 3 4 x 3 2 ； 由 33 42 6 yx y x ， 解得： 2 1 12 4 2 3 3 2 x x yy ， ，C（4， 3 2 ） ， 由图象可知：当 x4 或 0 x2 时，y1y2故答案为 x4 或 0 x2 19 x xy ；43 2 【解析】原式 2 xy xy 2 (2 ) ()() xy xy xy 2 x xy ； 当 x2 2，y221 时， 原式 22 222 21 43 2 20文具店购进 A 种款式的笔袋 60 个，B 种款式的笔袋 40 个 【解析】解：设文具店购进 B 种款式的笔袋 x 个，则购进 A 种款式的笔袋( 20)x 个， 依题意，得： 81
22、0600 (1 10%) 20 xx ， 解得：40 x， 经检验，40 x是所列分式方程的解，且符合题意， 2060 x 答：文具店购进 A 种款式的笔袋 60 个，B 种款式的笔袋 40 个 21(1) k = 1； （2）2. 【解析】 （1）将点(1,3)代入y = kx + 2 得3 = k + 2 k = 1 （2） 由（1）得直线解析式为y = x + 2 令x = 0，得到与y轴交点为(0,2) 令y = 0，得到与x轴交点为(2,0) 直线与两坐标轴围成的三角形面积为S = 1 2 2 2 = 2 22 （1） 2 5 ； （2）公平，理由见解析 【解析】(1) P (选到女
23、生)= 102 15 105 (2)这个游戏公平理由如下 列表 2 3 4 5 2 / 5 6 7 3 5 / 7 8 4 6 7 / 9 5 7 8 9 / 共有 12 种等可能结果其中点数和为合数有 6 种，为质数有 6 种 P (点数和为合数)=P (点数和为质数)= 61 = 122 这个游戏公平 23 （1）3，0.3，15， （2）7080 x； （3）共有 24 名学生被选拔参加决赛 【解析】解： （1）90.1850（人) 600.063a ，50(921 32)15m ，15500.3b 故答案为：3，0.3，15 （2）抽取的学生共有 50 名，中位数是第 25、26 个数
24、据的平均数，第 25、26 个数据在第 3 组，所以小青 的测试成绩在7080 x范围内； （3） 22 60060024 509 1521 35 （人） 答：共有 24 名学生被选拔参加决赛 24 （1）见解析;（2）18 【解析】 （1）证明：AB=AC，AD 是 BC 边上的中线， BAD=CAD， AE=DE， EAD=EDA， EDA=CAD， DE/AC； （2）AD 是 BC 边上的中线，即 D 是 BC 的中点，DE/AC， DE 是 ABC 的中位线， BE=5， AE=DE=5，AB=10， AB=AC，AD 是 BC 边上的中线，BC=12 ADBC，BD=CD=6， 2
25、222 1068ADABBD ， AED 的周长为 5+5+8=18 25 （1）点 A（1，1） ，点 B（2，0） ，点 C（0，0） ； （2）y（x2）22 或 y（x1 5 2 ）2 1 5 2 【解析】解： （1）抛物线 yx22x 与 x 轴交于 B、C 两点， 0 x22x， x10，x22， 点 B（2，0） ，点 C（0，0） ， yx22x（x1）21， 点 A（1，1） ； （2）设平移后抛物线的表达式为：y（x1m）21n（m1） ， 点 D（m1，1n） ， y（x1m）21nx22 （1m）xm22mn， 点 E（0，m22mn） ， 如图 1，当点 D 在点 A
26、 的下方时，过点 A 作 AMy 轴于 N，过点 D 作 DMAM 于 M， ANEAMD90 ， 以 A、D、E、F 为顶点的四边形是正方形， AEAD，EAD90 ， EANDAM90 ， AENEAN90 ， AENDAM， AENDAM（AAS） ， ANDM，ENAM， 11（1n） ，m1（1）m22mn（1） ， n1，m3， 平移后抛物线的表达式为：y（x2）22； 如图 2，点 D 在点 A 上方时，过点 D 作 DMy 轴于 N，过点 A 作 AMDM 于 M， 同理可证 EDNDAM， DNAM，ENDM， m11n1，m22mn（1n）m11， m 35 2 ，n1 5
27、 2 ， 平移后抛物线的表达式为：y（x1 5 2 ）21 5 2 ， 综上所述：平移后抛物线的表达式为：y（x2）22 或 y（x1 5 2 ）21 5 2 26 （1）BPCE，BC CE； （2）BCCE成立，BPCE不成立，BP与CE的关系为 2CEBP ， 见解析； （3）2 或 14 【解析】 （1）如图，连接 AE， BABC，且60ABC， ABC 为等边三角形， 60ABCBACACB，AB=AC， PEPA，且60APE， APE 为等边三角形， 60PAE，AP=AE， BACPACPAEPAC， BAPCAE； 在 BAP 和 CAE 中， ABAC BAPCAE AP
28、AE ， ABPACE， BP=CE，ABPACE ， BDAC，BABC， 60ABC， ABP=30 ， 30ABPACE， 90ACEACB， BCCE 故答案为：BPCE，BCCE （2）BCCE成立，BPCE不成立，BP与CE的关系为 2CEBP 理由如下： 选图 2 证明：连接AE， 由题意可知：ABC、APE均为等腰直角三角形， 45BACPAE，2 ACAE ABAP ， BAPPADCAEPAD， 即BAPCAE； 又 ACAE ABAP ， BAPCAE， 2 CECA BPBA ，ACEABP， ABBC，BDAC， 45ABDCBDACBACE， 454590BCEBC
29、AACE， BCCE， BCCE， 2CEBP 选图 3 证明： 理由如下：连接AE， 由题意可知：ABC、APE均为等腰直角三角形， 45BACPAE，2 ACAE ABAP ， BACPADPAEPAD， 即BAPCAE， 又 ACAE ABAP ， BAPCAE， 2 CECA BPBA ，ACEABP， ABBC，BDAC， 45ABDCBDACBACE， 454590BCEBCAACE， BCCE， BCCE， 2CEBP ； （3）2CE 或 14 如图， 8AB， 4 2ADBD ， 5 2AP ， 在Rt APD中， 22 3 2PDAPAD ， 4 23 22BP ， 由（2）知： 2CEBP ， 222CE ； 如图，同理可得 3 2DP ， 4 23 27 2BP ， 7 2214CE 综上：CE的长为 2 或 14
