 2021年重庆市万州区中考数学联考试卷(含答案解析)
2021年重庆市万州区中考数学联考试卷(含答案解析)
《2021年重庆市万州区中考数学联考试卷(含答案解析)》由会员分享,可在线阅读,更多相关《2021年重庆市万州区中考数学联考试卷(含答案解析)(32页珍藏版)》请在七七文库上搜索。
1、2021 年重庆市万州区中考数学联考试卷年重庆市万州区中考数学联考试卷 一、选择题(本大题共一、选择题(本大题共 12 个小题,每小题个小题,每小题 4 分,共分,共 48 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。 17 的相反数是( ) A B7 C D7 2下列垃圾分类图标中,是轴对称图形的是( ) A可回收物 B厨余垃圾 C有害垃圾 D其他垃圾 3下列运算中,正确的是( ) Ax
2、3+x4x7 B2x23x46x8 C (3x2y)29x4y2 D 4下列命题中,是真命题的是( ) A同旁内角互补 B有两边及一角对应相等的两个三角形全等 C矩形的对角线互相平分 D多边形的内角和为 360 5如图,点 A,B,C,D 四点均在O 上,AOD68,AODC,则B 的度数为( ) A40 B60 C56 D68 6估算的运算结果应在( ) A6 与 7 之间 B7 与 8 之间 C8 与 9 之间 D9 与 10 之间 7 九章算术是我国古代数学的经典著作,书中记载:今有上禾七秉,损实一斗,益之下禾两秉,而实 一十斗;下禾八秉,益实一斗,于上禾二秉,而实一十斗问上、下禾实一秉
3、各几何?其意思为:现有 七捆上等稻子和两捆下等稻子打成谷子,再减去一斗谷子,最后得到十斗谷子;八捆下等稻子和两捆上 等稻子打成谷子,再加上一斗谷子,最后得到十斗谷子问一捆上等稻子和一捆下等稻子各打谷子多少 斗?设一捆上等稻子和一捆下等稻子分别打成谷子 x 斗,y 斗,则可建立方程组为( ) A B C D 8 如图, 下列图形都是由黑色和白色的棋子按一定的规律排列组成的, 其中第个图形中有 2 颗黑色棋子, 第个图形中有 8 颗黑色棋子,第个图形中有将 17 颗黑色棋子按此规体, 则第个图中黑色棋子 的颗数是( ) A83 B104 C70 D99 9今年春天,红梅、李花、桃花争相盛开,重庆“
4、开往春天的列车”火爆全网重庆育才中学初三学生小 陶来到佛图关公园附近的观景台上开展数学实践活动如图,轻轨站上停靠着一辆长度为 200 米的轻轨 列车 AB,小陶从轨道正上方观景台 C 处先沿直线步行一段距离到达点 D 处后,他再沿着坡度为 i1: 2.4 的斜坡 DE 走了 28.6 米到另一观景台点 E 处,在点 E 处测得停靠在车站的轻轨车头端点 A 的俯角为 50,测得车尾端点 B 的俯角为 14 度如图,若点 A、B、C、D、E、F 在同一平面内,点 A、B、F 在 同一水平线上,则观景台 C 点距离轻轨轨道的竖直高度 CF 约为( )米 (结果保留一位小数,参考 数据:sin140.
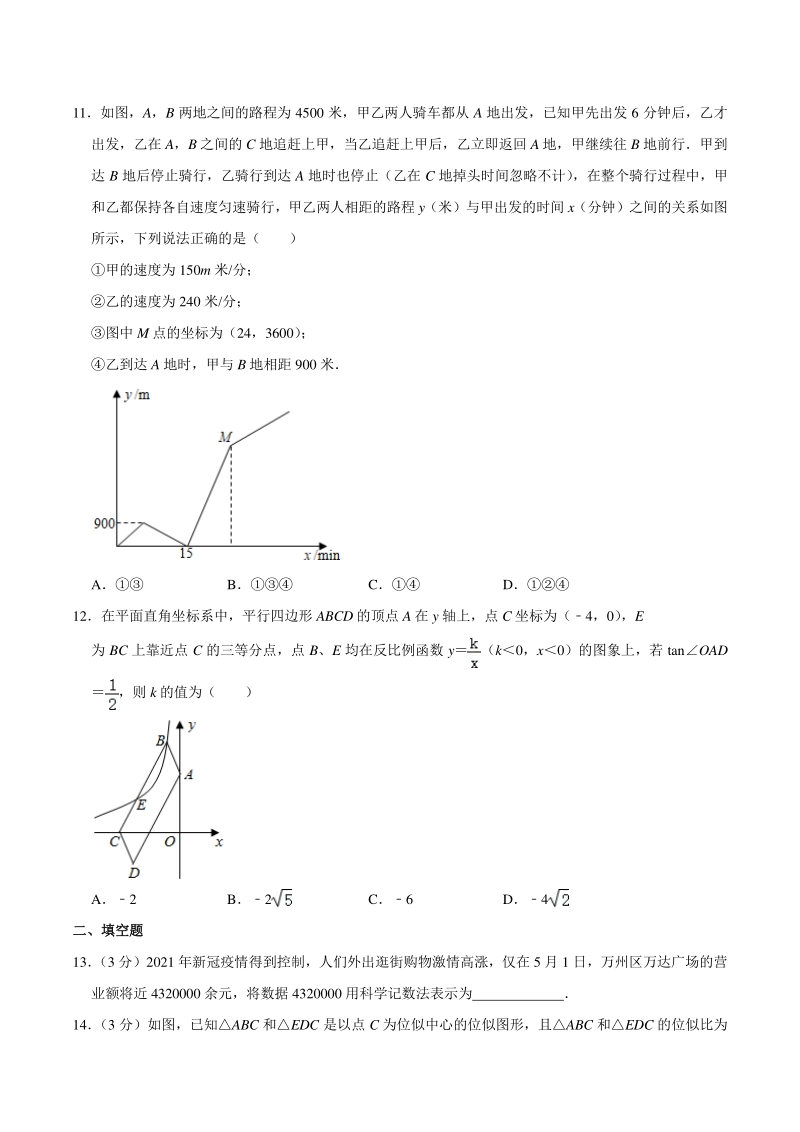
5、24,cos140.9,tan140.25;sin500.77,cos500.64,tan501.2) A39.1 B47.3 C52.2 D63.2 10若关于 x 的一元一次不等式组的解集为 x5,且关于 x 的分式方程+2 有非负整数解,则符合条件的所有整数 a 的和为( ) A1 B2 C3 D0 11如图,A,B 两地之间的路程为 4500 米,甲乙两人骑车都从 A 地出发,已知甲先出发 6 分钟后,乙才 出发,乙在 A,B 之间的 C 地追赶上甲,当乙追赶上甲后,乙立即返回 A 地,甲继续往 B 地前行甲到 达 B 地后停止骑行,乙骑行到达 A 地时也停止(乙在 C 地掉头时间忽略
6、不计) ,在整个骑行过程中,甲 和乙都保持各自速度匀速骑行,甲乙两人相距的路程 y(米)与甲出发的时间 x(分钟)之间的关系如图 所示,下列说法正确的是( ) 甲的速度为 150m 米/分; 乙的速度为 240 米/分; 图中 M 点的坐标为(24,3600) ; 乙到达 A 地时,甲与 B 地相距 900 米 A B C D 12在平面直角坐标系中,平行四边形 ABCD 的顶点 A 在 y 轴上,点 C 坐标为(4,0) ,E 为 BC 上靠近点 C 的三等分点,点 B、E 均在反比例函数 y(k0,x0)的图象上,若 tanOAD ,则 k 的值为( ) A2 B2 C6 D4 二、填空题
7、二、填空题 13 (3 分)2021 年新冠疫情得到控制,人们外出逛街购物激情高涨,仅在 5 月 1 日,万州区万达广场的营 业额将近 4320000 余元,将数据 4320000 用科学记数法表示为 14 (3 分)如图,已知ABC 和EDC 是以点 C 为位似中心的位似图形,且ABC 和EDC 的位似比为 1:2,ABC 面积为 4,则EDC 的面积是 15 (3 分)在五个完全相同的小球上分别写上 1,2,3,4,5 五个数字,然后装入一个不透明的口袋内搅 匀,从口袋内取出一个球记下数字后作为点 P 的横坐标 x,放回袋中搅匀,然后再从口袋中取出一个球 记下数字后作为点 P 的纵坐标 y
8、则在坐标平面内,点 P(x,y)落在直线 yx+5 上的概率 是 16 (3 分)如图, 在菱形 ABCD 中, BC4,ADC120,以 A 为圆心, AD 为半径画弧, 交 AC 于点 E, 过点 E 作 EFAB 交 AD 于点 F,则阴影部分的面积为 (结果保留根号与 ) 17 (3 分)如图,在矩形 ABCD 中,AB10,点 E 是 AD 边上的一点,将ABE 沿着 BE 折叠,点 A 刚好 落在 CD 边上点 G 处,点 F 为 CG 上的一点,将BCF 沿着 BF 折叠,点 C 恰好落在 BG 上点 H 处,若 SBCF:SBGF3:5,连接 AG,则点 H 到 AG 的距离为
9、 18 (3 分)为迎接“五一节”的到来,某水果店推出了 A、B、C 三类礼包,已知这三类礼包均由苹果、芒 果、草莓三种水果搭配而成,每袋礼包的成本均为苹果、芒果、草莓三种水果成本之和每袋 A 类礼包 有 5 斤苹果、2 斤芒果、8 斤草莓;每袋 C 类礼包有 7 斤苹果、1 斤芒果、4 斤草莓已知每袋 A 的成本 是该袋中苹果成本的 3 倍,利润率为 30%,每袋 B 的成本是其售价的,利润是每袋 A 利润的;每袋 C 礼包利润率为 25%若该网店 12 月 12 日当天销售 A、B、C 三种礼包袋数之比为 4:6:5,则当天该 水果店销售总利润率为 三、解答题三、解答题 19计算: (1)
10、 (x2) (x+2)(x2)2; (2) (a+1) 20 (10 分)如图,已知等边ABC 中边 AB10,按要求解答下列问题: (1)尺规作图:作ABC 的角平分线 BP,射线 BP 交边 AC 于点 P (不写作法,用 2B 铅笔作图并保留 痕迹) (2)在(1)作图中,若点 D 在线段 BP 上,且使得 AD5,求 BD 的长 (结果保留根号) 21随着冬季的来临, “新冠”疫情再次肆虐,育才中学为确保学生健康,开展了“远离新冠珍爱生命”的 防 “新冠” 安全知识竞赛 现从该校七、 八年级中各随机抽取 10 名学生的竞赛成绩 (百分制) 进行整理、 描述和分析 (成绩得分用 x 表示
11、, 共分成四组, A.80 x85; B.85x90, C.90 x95, D.95x100) , 下面给出了部分信息:七年级 10 名学生的竞赛成绩是:80,86,99,96,90,99,100,82,89,99; 八年级 10 名学生的竞赛成绩在 C 组中的数据是:94,94,90 七、八年级抽取的学生竞赛成绩统计表 年级 七年级 八年级 平均数 92 92 中位数 93 b 众数 c 100 方差 52 50.4 根据以上信息,解答下列问题: (1)直接写出上述图表中 a,b,c 的值; (2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防“新冠”安全知识更好?请说明理由 (一条
12、即可) ; (3) 育才中学七、 八年级共 2160 人参加了此次竞赛活动, 估计参加此次竞赛活动获得成绩优秀 (x95) 的学生人数是多少? 22在函数的学习中,我们经历“确定函数表达式画函数图象利用函数图象研究函数性质利 用图象解决问题”的学习过程,画函数图象时,我们常通过描点或平移或翻折的方法画函数图象,请根 据你学到的函数知识探究函数 y1的图象与性质并利用图象解决如下问题: 列出 y1与 x 的几组对应的值如表: x 3 2 1 0 1 2 3 4 5 y m 0 1 2 1 0 n (1)根据表格中 x、y 的对应关系可得 m ,n ; (2)用你喜欢的方式画出该函数图象:根据函数
13、图象,写出该函数的一条性质: ; (3)直接写出当函数 y1的图象与直线 y2kx+1 有三个交点时,k 的取值范围是 23根据农业部提出“大力发展农村产业,实现乡村全面振兴”的方针,我市精准扶贫,指导某县大力发 展枇杷种植,去年、今年枇杷产量连续获得大丰收该县某种植户枇杷销售采用线下销售和线上销售两 种模式 (1)今年该种植户枇杷产量为 4500 千克,全部售出,其中线上销量不超过线下销量的 4 倍求线下销 量至少多少千克? (2)该种植户去年枇杷线下销售均价为 15 元/千克,销售量为 900 千克线上销售均价为 12 元/千克, 销售量为 1800 千克今年线下销售均价上涨了 a%,但销
14、售量下降了 2a%,线上销售均价上涨了a%, 销量与去年持平,今年枇杷的销售总金额比去年销售总金额减少了a%,求 a 的值 24 若一个四位自然数满足千位数字比十位数字大 2, 百位数字比个位数字大 2, 我们称这个数为 “多多数” 将 “多多数”m 各个数位上的数字倒序排列可得到一个新的四位数 m,记 F(m)例如: m3412,m2143,则 F(3412)1 (1)判断 6543 和 4231 是否为“多多数”?请说明理由; (2)若 A 和 B 为两个“多多数” ,其中 A 的十位数字为 6,B 的个位数字为 2,且满足 F(A) F(B) 35,求 AB 的值 25在平面直角坐标系
15、xOy 中,抛物线 yx22x6 与 x 轴交于点 A、B(点 A 在点 B 左侧) ,与 y 轴交 于点 C,顶点为点 D (1)求点 B、D 的坐标; (2)如图 1,点 P 在直线 BD 下方抛物线上运动(不含端点 B、D) ,记PCB 的面积为 S1,记PDB 的面积为 S2,求 2S1S2的最大值及此时点 P 的坐标; (3)如图 2,将该抛物线沿直线 DB 平移,设平移后的新抛物线的顶点为 D(D与 D 不重合) ,新抛物 线与直线 DB 的另一个交点为点 E,在平面直角坐标系中是否存在点 F,使以点 C、D、E、F 为顶点的 四边形为矩形?若存在,直接写出点 F 的坐标;若不存在
16、,请说明理由 26如图,点 B,C,D 在同一条直线上,BCF 和ACD 都是等腰直角三角形连接 AB,DF,延长 DF 交 AB 于点 E (1)如图 1,若 ADBD,DE 是ABD 的平分线,BC1,求 CD 的长度; (2)如图 2,连接 CE,求证:DECE+AE; (3)如图 3,改变BCF 的大小,始终保持点 F 在线段 AC 上(点 F 与点 A,C 不重合) 将 ED 绕点 E 顺时针旋转 90得到 EP取 AD 的中点 O,连接 OP当 AC2 时,直接写出 OP 长度的最大值 2021 年重庆市万州区中考数学联考试卷年重庆市万州区中考数学联考试卷 参考答案与试题解析参考答
17、案与试题解析 一、选择题(本大题共一、选择题(本大题共 12 个小题,每小题个小题,每小题 4 分,共分,共 48 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。 17 的相反数是( ) A B7 C D7 【分析】只有符号不同的两个数互为相反数 【解答】解:根据相反数的定义,7 的相反数是+7,即 7 故选:B 2下列垃圾分类图标中,是轴对称图形的是( ) A可回收物 B厨余垃圾 C有害垃
18、圾 D其他垃圾 【分析】根据轴对称图形的概念对各选项分析判断即可得解 【解答】解:A、不是轴对称图形,故本选项不合题意; B、不是轴对称图形,故本选项不合题意; C、不是轴对称图形,故本选项不合题意; D、是轴对称图形,故本选项符合题意 故选:D 3下列运算中,正确的是( ) Ax3+x4x7 B2x23x46x8 C (3x2y)29x4y2 D 【分析】直接利用合并同类项法则以及积的乘方运算法则、单项式乘单项式、二次根式的乘法运算法则 分别计算得出答案 【解答】解:A、x3+x4无法合并,故此选项错误; B、2x23x46x6,故此选项错误; C、 (3x2y)29x4y2,故此选项错误;
19、 D、,故此选项正确 故选:D 4下列命题中,是真命题的是( ) A同旁内角互补 B有两边及一角对应相等的两个三角形全等 C矩形的对角线互相平分 D多边形的内角和为 360 【分析】利用平行线的性质、全等三角形的判定、矩形的性质及多边形的内角和的知识分别判断后即可 确定正确的选项 【解答】解:A、两直线平行,同旁内角互补,故原命题错误,是假命题,不符合题意; B、有两边及夹对应相等的两个三角形全等,故原命题错误,是假命题,不符合题意; C、矩形的对角线互相平分,正确,是真命题,符合题意; D、多边形的内角和为(n2)180,故原命题错误,是假命题,不符合题意, 故选:C 5如图,点 A,B,C
20、,D 四点均在O 上,AOD68,AODC,则B 的度数为( ) A40 B60 C56 D68 【分析】 接 OC, 由 AODC, 得出ODCAOD68, 再由 ODOC, 得出ODCOCD68, 求得COD44,进一步得出AOC,进一步利用圆周角定理得出B 的度数即可 【解答】解:如图, 连接 OC, AODC, ODCAOD68, ODOC, ODCOCD68, COD44, AOC112, BAOC56 故选:C 6估算的运算结果应在( ) A6 与 7 之间 B7 与 8 之间 C8 与 9 之间 D9 与 10 之间 【分析】先根据二次根式的乘法法则:两个二次根式相乘,被开方数相
21、乘,根指数不变,作为积中的被 开方数,再利用夹逼法可得 45,从而进一步可判断出答案 【解答】解:原式+4+, 45, 84+9, 即+的值在 8 和 9 之间 故选:C 7 九章算术是我国古代数学的经典著作,书中记载:今有上禾七秉,损实一斗,益之下禾两秉,而实 一十斗;下禾八秉,益实一斗,于上禾二秉,而实一十斗问上、下禾实一秉各几何?其意思为:现有 七捆上等稻子和两捆下等稻子打成谷子,再减去一斗谷子,最后得到十斗谷子;八捆下等稻子和两捆上 等稻子打成谷子,再加上一斗谷子,最后得到十斗谷子问一捆上等稻子和一捆下等稻子各打谷子多少 斗?设一捆上等稻子和一捆下等稻子分别打成谷子 x 斗,y 斗,则
22、可建立方程组为( ) A B C D 【分析】根据“七捆上等稻子和两捆下等稻子打成谷子,再减去一斗谷子,最后得到十斗谷子;八捆下 等稻子和两捆上等稻子打成谷子,再加上一斗谷子,最后得到十斗谷子” ,即可得出关于 x,y 的二元一 次方程组,此题得解 【解答】解:依题意得: 故选:C 8 如图, 下列图形都是由黑色和白色的棋子按一定的规律排列组成的, 其中第个图形中有 2 颗黑色棋子, 第个图形中有 8 颗黑色棋子,第个图形中有将 17 颗黑色棋子按此规体, 则第个图中黑色棋子 的颗数是( ) A83 B104 C70 D99 【分析】设第 n 个图形中有 an颗黑色棋子(n 为正整数) ,根据
23、各图形中黑色棋子数的变化可找出变化规 律“ann(n+1)1(n 为正整数) ” ,再代入 n7 即可求出结论 【解答】解:设第 n 个图形中有 an颗黑色棋子(n 为正整数) , a1212,a23318,a3451217,a45712329, an(n+1) (2n1)12(n1)(n+1) (2n1)n(n+1)1 (n 为正整数) , a77(7+1)183 故选:A 9今年春天,红梅、李花、桃花争相盛开,重庆“开往春天的列车”火爆全网重庆育才中学初三学生小 陶来到佛图关公园附近的观景台上开展数学实践活动如图,轻轨站上停靠着一辆长度为 200 米的轻轨 列车 AB,小陶从轨道正上方观景
24、台 C 处先沿直线步行一段距离到达点 D 处后,他再沿着坡度为 i1: 2.4 的斜坡 DE 走了 28.6 米到另一观景台点 E 处,在点 E 处测得停靠在车站的轻轨车头端点 A 的俯角为 50,测得车尾端点 B 的俯角为 14 度如图,若点 A、B、C、D、E、F 在同一平面内,点 A、B、F 在 同一水平线上,则观景台 C 点距离轻轨轨道的竖直高度 CF 约为( )米 (结果保留一位小数,参考 数据:sin140.24,cos140.9,tan140.25;sin500.77,cos500.64,tan501.2) A39.1 B47.3 C52.2 D63.2 【分析】 过 E 作 E


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 重庆市 万州区 中考 数学 联考 试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-185579.html