 2021年山东省德州市乐陵市中考数学一模试卷(含答案详解)
2021年山东省德州市乐陵市中考数学一模试卷(含答案详解)
《2021年山东省德州市乐陵市中考数学一模试卷(含答案详解)》由会员分享,可在线阅读,更多相关《2021年山东省德州市乐陵市中考数学一模试卷(含答案详解)(27页珍藏版)》请在七七文库上搜索。
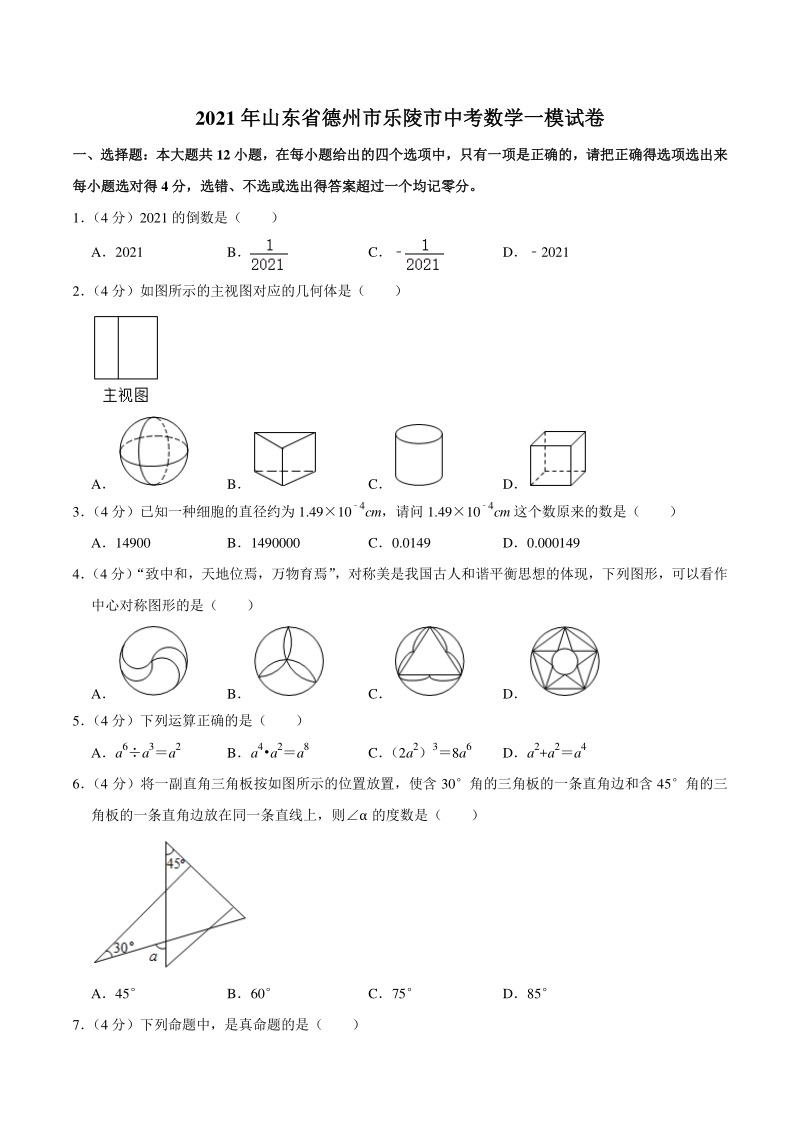
1、2021 年山东省德州市乐陵市中考数学一模试卷年山东省德州市乐陵市中考数学一模试卷 一、选择题:本大题共一、选择题:本大题共 12 小题,在每小题给出的四个选项中,只有一项是正确的,请把正确得选项选出来小题,在每小题给出的四个选项中,只有一项是正确的,请把正确得选项选出来 每小题选对得每小题选对得 4 分,选错、不选或选出得答案超过一个均记零分。分,选错、不选或选出得答案超过一个均记零分。 1 (4 分)2021 的倒数是( ) A2021 B C D2021 2 (4 分)如图所示的主视图对应的几何体是( ) A B C D 3 (4 分)已知一种细胞的直径约为 1.4910 4cm,请问
2、1.49104cm 这个数原来的数是( ) A14900 B1490000 C0.0149 D0.000149 4 (4 分) “致中和,天地位焉,万物育焉” ,对称美是我国古人和谐平衡思想的体现,下列图形,可以看作 中心对称图形的是( ) A B C D 5 (4 分)下列运算正确的是( ) Aa6a3a2 Ba4a2a8 C (2a2)38a6 Da2+a2a4 6 (4 分)将一副直角三角板按如图所示的位置放置,使含 30角的三角板的一条直角边和含 45角的三 角板的一条直角边放在同一条直线上,则 的度数是( ) A45 B60 C75 D85 7 (4 分)下列命题中,是真命题的是(
3、) A一组对边平行,另一组对边相等的四边形是平行四边形 B两边及其中一边的对角分别相等的两个三角形全等 C两条直线被第三条直线所截,内错角相等 D对角线互相垂直的平行四边形是菱形 8 (4 分) 孙子算经中有一道题,原文是: “今有木,不知长短引绳度之,余绳四尺五寸;屈绳量之, 不足一尺木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 4.5 尺将绳子对折再量长木, 长木还剩余 1 尺,问木长多少尺,现设绳长 x 尺,木长 y 尺,则可列二元一次方程组为( ) A B C D 9 (4 分)若关于 x 的方程+2 的解为正数,则 m 的取值范围是( ) Am6 Bm6 Cm6 且 m0
4、Dm6 且 m8 10 (4 分)为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内 每立方米空气中含药量 y(mg)与时间 t(h)成正比例;药物释放完毕后,y 与 t 成反比例,如图所示根 据图象信息,下列选项错误的是( ) A药物释放过程需要小时 B药物释放过程中,y 与 t 的函数表达式是 yt C空气中含药量大于等于 0.5mg/m3的时间为h D若当空气中含药量降低到 0.25mg/m3以下时对身体无害,那么从消毒开始,至少需要经过 4.5 小时学 生才能进入教室 11 (4 分)如图,分别以等边三角形 ABC 的三个顶点为圆心,以边长为半径画弧,得
5、到的封闭图形是莱洛 三角形,若 AB2,则莱洛三角形的面积(即阴影部分面积)为( ) A B C2 D2 12 (4 分)如图,OA1B1,A1A2B2,A2A3B3,是分别以 A1,A2,A3,为直角顶点,一条直角边 在 x 轴正半轴上的等腰直角三角形,其斜边的中点 C1(x1,y1) ,C2(x2,y2) ,C3(x3,y3) ,在反比 例函数 y(x0)的图象上则 y1+y2+y2021的值为( ) A2 B900 C2 D4 二、填空题:本大题共二、填空题:本大题共 6 小题,共小题,共 24 分,只要求填写最后的结果,每小题填对得分,只要求填写最后的结果,每小题填对得 4 分分. 1
6、3 (4 分) 九章算术中注有“今两算得失相反,要令正负以名之” ,意思是:今有两数若其意义相反, 则分别叫做正数与负数,若气温为零上 10记作+10,则3表示气温为 14 (4 分)一个不透明的盒子中装有 1 个红球,2 个黄球和 1 个绿球,这些球除了颜色外无其他差别,从 中随机摸出一个小球,恰好是黄球的概率为 15 (4 分)菱形的一条对角线长为 8,其边长是方程 x29x+200 的一个根,则该菱形的周长为 16 (4 分)阅读理解:用“十字相乘法”分解因式 2x2x3 的方法 (1)二次项系数 212; (2)常数项3131(3) ,验算: “交叉相乘之和” ; 13+2(1)1 1
7、(1)+235 1(3)+211 11+2(3) 5 (3)发现第个“交叉相乘之和”的结果 1(3)+211,等于一次项系数1 即: (x+1) (2x3)2x23x+2x32x2x3,则 2x2x3(x+1) (2x3) 像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫做十字相乘法仿照以上方法,分解 因式:3x2+5x12 17 (4 分)如图,在 RtABC 中,C90,AC6,BC8,P 为 AB 边上不与 A,B 重合的一动点, 过点 P 分别作 PEAC 于点 E,PFBC 于点 F,则线段 EF 的最小值是 18 (4 分)如图,矩形 ABCD 中,AC,BD 相交于点
8、O,过点 B 作 BFAC 交 CD 于点 F,交 AC 于点 M, 过点 D 作 DEBF 交 AB 于点 E,交 AC 于点 N,连接 FN,EM则下列结论: DNBM;EMFN;AEFC;当 AOAD 时,四边形 DEBF 是菱形 其中,正确的序号为: 三、解答题:本大题共三、解答题:本大题共 7 小题,共小题,共 78 分解答要求写出必要的文字说明、证明过程或演算步骤分解答要求写出必要的文字说明、证明过程或演算步骤. 19 (8 分)已知:a2+3a20,求代数的值 20 (10 分)为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平 相当的初三年级进行
9、调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为 150 分)分为 5 组(从左到右的顺序) 统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计 图观察图形的信息,回答下列问题: (1)本次调查共随机抽取了该年级 名学生,并将频数分布直方图补充完整; (2)估计该年级 1500 名考生中,考试成绩 120 分以上(合 120 分)学生有 名; (3)扇形统计图中,第二组所占圆心角的度数为 (4)如果第一组(7590)中只有一名是女生,第五组(135150)中只有一名是男生,针对考试成绩 情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想请你用列表
10、或画树状图 的方法求出所选两名学生刚好是一名女生和一名男生的概 率 21 (10 分)小乐(甲) 、小陵(乙)两人相约周末沿同一条路线登山,小乐、小陵两人距地面的高度 y(米) 与登山时间 x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: (1)小乐登山的速度是每分钟 米;小陵在 A 地提速时,小乐距地面的高度为 米; (2)若小陵提速后,小陵的速度是小乐登山速度的 3 倍; 求小陵登山全过程中,登山时距地面的高度 y(米)与登山时间 x(分钟)之间的函数解析式; 小陵计划在他提速后 5 分钟内追上小乐,请判断小陵的计划能实现吗?并说明理由 22 (12 分)如图,在ABC
11、 中,ACBC,AB26,以 AB 为直径的O 交 AC 边于点 D,点 E 在 BC 上, 连接 BD,DE,CDEABD (1)证明:DE 是O 的切线; (2)若 sinCDE,求 DC 的长 23 (12 分)用电脑程序控制小型赛车进行 50m 比赛, “畅想号”和“和谐号”两辆赛车进入了决赛比赛 前的练习中,两辆车从起点同时出发, “畅想号” 到达终点时, “和谐号”离终点还差 3m 已知 “畅想号” 的平均速度为 2.5m/s (1)求“和谐号”的平均速度; (2)如果两车重新开始比赛, “畅想号”从起点向后退 3m,两车同时出发,两车能否同时到达终点?若 能,求出两车到达终点的时
12、间;若不能,请重新调整一辆车的平均速度,使两车能同时到达终点 24 (12 分)随着教育教学改革的不断深入,数学教学如何改革和发展,如何从“重教轻学”向自主学习探 索为主的方向发展, 是一个值得思考的问题 从数学的产生和发展历程来看分析, 不外乎就是三个环节: 观察猜想探究证明拓展延伸下面同学们从这三个方面试着解决下列问题: 已知:如图 1 所示,将一块等腰三角板 BMN 放置与正方形 ABCD 的B 重合,连接 AN、CM,E 是 AN 的中点,连接 BE 观察精想 (1)CM 与 BE 的数量关系是 ,CM 与 BE 的位置关系是 ; 探究证明 (2)如图 2 所示,把三角板 BMN 绕点
13、 B 逆时针旋转 (090) ,其他条件不变,线段 CM 与 BE 的 关系是否仍然成立,并说明理由; 拓展延伸 (3)若旋转角 45,且NBE2ABE,求的值 25 (14 分)如图,抛物线 yax2+bx+2 与 x 轴交于 A,B 两点,且 OA2OB,与 y 轴交于点 C,连接 BC, 抛物线对称轴为直线 x,D 为第一象限内抛物线上一动点,过点 D 作 DEOA 于点 E,与 AC 交于 点 F,设点 D 的横坐标为 m (1)求抛物线的表达式; (2)当线段 DF 的长度最大时,求 D 点的坐标; (3) 抛物线上是否存在点 D, 使得以点 O, D, E 为顶点的三角形与BOC
14、相似?若存在, 求出 m 的值; 若不存在,请说明理由 2021 年山东省德州市乐陵市中考数学一模试卷年山东省德州市乐陵市中考数学一模试卷 参考答案与试题解析参考答案与试题解析 一、选择题:本大题共一、选择题:本大题共 12 小题,在每小题给出的四个选项中,只有一项是正确的,请把正确得选项选出来小题,在每小题给出的四个选项中,只有一项是正确的,请把正确得选项选出来 每小题选对得每小题选对得 4 分,选错、不选或选出得答案超过一个均记零分。分,选错、不选或选出得答案超过一个均记零分。 1 (4 分)2021 的倒数是( ) A2021 B C D2021 【解答】解:2021 的倒数是: 故选:
15、B 2 (4 分)如图所示的主视图对应的几何体是( ) A B C D 【解答】解:A、主视图为,故此选项不合题意; B、主视图为,故此选项符合题意; C、主视图为,故此选项不合题意; D、主视图为,故此选项不合题意 故选:B 3 (4 分)已知一种细胞的直径约为 1.4910 4cm,请问 1.49104cm 这个数原来的数是( ) A14900 B1490000 C0.0149 D0.000149 【解答】解:1.4910 40.000149, 故选:D 4 (4 分) “致中和,天地位焉,万物育焉” ,对称美是我国古人和谐平衡思想的体现,下列图形,可以看作 中心对称图形的是( ) A B
16、 C D 【解答】解:A、是中心对称图形,故本选项符合题意; B、不是中心对称图形,故本选项不符合题意; C、不是中心对称图形,故本选项不符合题意; D、不是中心对称图形,故本选项不符合题意 故选:A 5 (4 分)下列运算正确的是( ) Aa6a3a2 Ba4a2a8 C (2a2)38a6 Da2+a2a4 【解答】解:A、a6a3a3,故本选项不合题意; B、a4a2a6,故本选项不合题意; C、 (2a2)38a6,故本选项符合题意; D、a2+a22a2,故本选项不合题意; 故选:C 6 (4 分)将一副直角三角板按如图所示的位置放置,使含 30角的三角板的一条直角边和含 45角的三
17、 角板的一条直角边放在同一条直线上,则 的度数是( ) A45 B60 C75 D85 【解答】解:如图, ACD90, FCG180ACD90, F45, CGFDGB904545, D30, D+DGB30+4575, 故选:C 7 (4 分)下列命题中,是真命题的是( ) A一组对边平行,另一组对边相等的四边形是平行四边形 B两边及其中一边的对角分别相等的两个三角形全等 C两条直线被第三条直线所截,内错角相等 D对角线互相垂直的平行四边形是菱形 【解答】解:A、一组对边平行,另一组对边相等的四边形可能是平行四边形,也可能是等腰梯形,故 原命题错误,是假命题,不符合题意; B、两边及夹角分
18、别相等的两个三角形全等,故原命题错误,是假命题,不符合题意; C、两条平行直线被第三条直线所截,内错角相等,故原命题错误,是假命题,不符合题意; D、对角线互相垂直的平行四边形是菱形,正确,是真命题,符合题意, 故选:D 8 (4 分) 孙子算经中有一道题,原文是: “今有木,不知长短引绳度之,余绳四尺五寸;屈绳量之, 不足一尺木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 4.5 尺将绳子对折再量长木, 长木还剩余 1 尺,问木长多少尺,现设绳长 x 尺,木长 y 尺,则可列二元一次方程组为( ) A B C D 【解答】解:设绳长 x 尺,木长为 y 尺, 依题意得, 故选:B 9
19、 (4 分)若关于 x 的方程+2 的解为正数,则 m 的取值范围是( ) Am6 Bm6 Cm6 且 m0 Dm6 且 m8 【解答】解:原方程化为整式方程得:2xm2(x2) , 解得:x2, 因为关于 x 的方程+2 的解为正数, 可得:, 解得:m6, 因为 x2 时原方程无解, 所以可得, 解得:m0 故选:C 10 (4 分)为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内 每立方米空气中含药量 y(mg)与时间 t(h)成正比例;药物释放完毕后,y 与 t 成反比例,如图所示根 据图象信息,下列选项错误的是( ) A药物释放过程需要小时 B药物释
20、放过程中,y 与 t 的函数表达式是 yt C空气中含药量大于等于 0.5mg/m3的时间为h D若当空气中含药量降低到 0.25mg/m3以下时对身体无害,那么从消毒开始,至少需要经过 4.5 小时学 生才能进入教室 【解答】解:设正比例函数解析式是 ykt, 反比例函数解析式是 y, 把点(3,)分别代入反比例函数解析式得:, 解得:m, 反比例函数解析式是 y, 当 y1 时,代入上式得 t, 把 t时,y1 代入正比例函数解析式是 ykt 得:k, 正比例函数解析式是 yt, A由图象知,y1 时,t,即药物释放过程需要小时,故 A 不符合题意; B药物释放过程中,y 与 t 的成正比


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 山东省 德州市 乐陵市 中考 数学 试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 2021德州数学中考
- 2019年山东省德州市乐陵市中考数学一模试卷含答案解析
- 2021年西藏日喀则市中考数学一模试卷含答案详解
- 2019年山东省德州市陵城区中考数学一模试卷含答案解析
- 2021年山东省青岛市市南区中考数学一模试卷含答案详解
- 2020年山东省德州市乐陵市中考化学一模试卷含答案解析
- 2021年山东省枣庄市薛城区中考数学一模试卷含答案详解
- 2019年山东省德州市乐陵市中考化学二模试卷含答案解析
- 山东省德州市乐陵市中考数学二模试卷含答案解析
- 2021年山东省德州市乐陵市中考数学一模试卷含答案详解
- 2021年山东省德州市宁津县中考数学一模小练兵试卷含答案
- 2021 德州 中考 数学
- 2021年山东省德州市庆云县中考数学一模试卷含答案解析
- 2021年山东省德州市乐陵市中考二模数学试卷含答案解析
- 2021年山东省德州市乐陵市中考二模数学试卷含答案解



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-184926.html