 2021年重庆市沙坪坝区中考数学强化训练试卷(二)含答案解析
2021年重庆市沙坪坝区中考数学强化训练试卷(二)含答案解析
《2021年重庆市沙坪坝区中考数学强化训练试卷(二)含答案解析》由会员分享,可在线阅读,更多相关《2021年重庆市沙坪坝区中考数学强化训练试卷(二)含答案解析(35页珍藏版)》请在七七文库上搜索。
1、2021 年重庆市沙坪坝区中考数学强化训练试卷(二) 一、选择题: (本大题 12 个小题,每小题 4 分。共 48 分)在每个小题的下面,都给出了代号 为 A,B,C,D 的四个答案。其中只有一个是正确的,请将答题卡上题号右侧正确答案所对 应的方框涂黑。 1.下列数字中最小的数为( ) A2 B1 C0 D 2.由五个小立方体搭成如图的几何体,从正面看到的平面图形是( ) A B C D 3.估计+2 的值在( ) A0 到 1 之间 B1 到 2 之间 C2 到 3 之间 D3 到 4 之间 4.下列计算正确的是( ) Aa3+a3a6 B3aa2 C (a2)3a5 Daa2a3 5.下
2、列命题,真命题是( ) A一组对边平行,另一组对边相等的四边形是平行四边形 B有一个角为直角的四边形为矩形 C对角线互相垂直的四边形是菱形 D一组邻边相等的矩形是正方形 6.孙子算经中有一道题: “今有木,不知长短引绳度之,余绳四尺五,屈绳量之,不足一尺问木长 几何?”译文大致是: “用一根绳子去量一根木条,绳子剩余 4.5 尺;将绳子对折再量木条,木条剩余 1 尺,问木条长多少尺 ”如果设木条长为 x 尺,绳子长为 y 尺,根据题意列方程组正确的是( ) A B C D 7.如图,P 是O 外一点,PA 是O 的切线,A 为切点,PO 与O 相交于 B 点,已知BCA34,C 为 O 上一点
3、,连接 CA,CB,则P 的度数为( ) A34 B56 C22 D28 8.如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比 为,点 A,B,E 在 x 轴上若正方形 ABCD 的边长为 2,则点 F 坐标为( ) A (8,6) B (9,6) C D (10,6) 9.一天,小明和朋友一起到小区测量小明所住楼房的高度,他们首先在 A 测得楼房顶部 E 的仰角为 37, 然后沿着斜坡 AB 走了 7.8 米到 B 处,再测得楼房顶部 E 的仰角为 45,身高忽略不计已知斜坡 AB 的坡度 i1:2.4,楼房 EF 所离 BC 高度
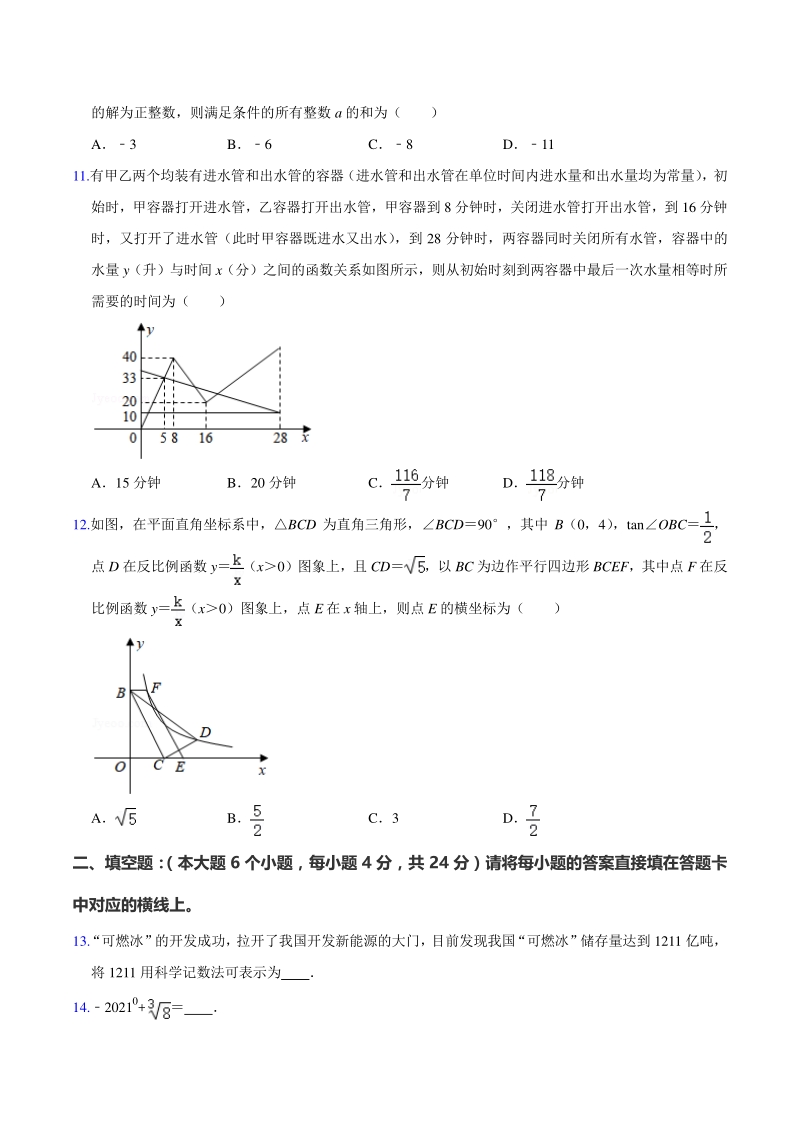
4、CD 为 1.8 米则楼房自身高度 EF 大约为( )米 (参考数据:sin370.60,cos370.80,tan370.75) A40.8 B33.6 C31.8 D30.6 10.已知关于 x 的一元一次不等式组的解集为 x7, 且关于 y 的分式方程1 的解为正整数,则满足条件的所有整数 a 的和为( ) A3 B6 C8 D11 11.有甲乙两个均装有进水管和出水管的容器(进水管和出水管在单位时间内进水量和出水量均为常量) ,初 始时,甲容器打开进水管,乙容器打开出水管,甲容器到 8 分钟时,关闭进水管打开出水管,到 16 分钟 时,又打开了进水管(此时甲容器既进水又出水) ,到 2
5、8 分钟时,两容器同时关闭所有水管,容器中的 水量 y(升)与时间 x(分)之间的函数关系如图所示,则从初始时刻到两容器中最后一次水量相等时所 需要的时间为( ) A15 分钟 B20 分钟 C分钟 D分钟 12.如图,在平面直角坐标系中,BCD 为直角三角形,BCD90,其中 B(0,4) ,tanOBC, 点 D 在反比例函数 y(x0)图象上,且 CD,以 BC 为边作平行四边形 BCEF,其中点 F 在反 比例函数 y(x0)图象上,点 E 在 x 轴上,则点 E 的横坐标为( ) A B C3 D 二、填空题: (本大题 6 个小题,每小题 4 分,共 24 分)请将每小题的答案直接
6、填在答题卡 中对应的横线上。 13. “可燃冰” 的开发成功, 拉开了我国开发新能源的大门, 目前发现我国 “可燃冰” 储存量达到 1211 亿吨, 将 1211 用科学记数法可表示为 14.20210+ 15.如图,在等边ABC 中,O 为 BC 中点,以 O 为圆心画弧 DE,弧 DE 分别与 AB、AC 相切于点 D、E, 若 BD1,则图中阴影部分的面积为 16.现有五张完全相同的不透明的卡片,其正面分别写有1,0,1,5,6 五个数把这五张卡片背面朝上 洗匀后放在桌上,小张先随面抽取一张卡片, 其上的数字记为 x, 小李再从剩下卡片中随机抽取一卡片, 其上的数字记为 y,这样确定了点
7、 P(x,y) ,则点 P 在直线 yx+5 的概率为 17.如图,在平行四边形 ABCD 中,A60,AB10,BC12,点 E、F 分别在边 CD、BC 上,将CEF 沿 EF 翻折得到CEF,若点 C 的对应点 C恰好落在 AD 边上,且满足 AC2CD,则点 E 到 BC 边的距 离为 18.端午将至,吃粽子是中华民族的传统粽子馅料有很多品种,比如素馅,肉馅,甜味馅去年某商人抓 住商机,购进素馅,肉馅,甜味馅三种粽子已知销售每袋素馅粽子的利润率为 10%,每袋肉馅粽子的 利润率为 20%,每袋甜味馅粽子的利润率为 30%,当售出的三种馅料粽子的袋数之比为 1:3:1 时,商 人得到的总
8、利润率为 22%; 当售出的三种馅料粽子的袋数之比为 3: 2: 1 时, 商人得到的总利润率为 20%, 那么当售出的三种馅料粽子的袋数之比为 2:3:4 时,这个商人得到的总利润率为 三、解答题(本大题 7 个小题,每小题 10 分,共 70 分)解答时每小题必须给出必要的演算 过程或推理步骤,画出必要的图形(包括辅助线) 。请将解答过程书写在答题卷中对应的位置 上。 19.化简: (1) (x+2) (x3)(x2)2 (2) 20.如图,已知ABC,在 BC 的延长线上取一点 D 使得 ADAC (1)在 AC 左侧,求作点 E,使得 AEAB,CEDB,连接 AE、CE (用基本作图
9、,保留作图痕迹, 不写作法、结论 ) (2)求证:EABCAD 21.重庆是一个非常适合旅游打卡的城市,在渝中区有“洪崖洞” ,南岸区有“南山一颗树”等等,为了解初 三学生对重庆历史文化的了解程度, 随机抽取了男、 女各 m 名学生进行问卷测试, 问卷共 30 道选择题, 现将得分情况统计,并绘制了如图不完整的统计图(数据分组为 A 组:x18,B 组:18x22,C 组: 22x26,D 组:26x30,x 表示问卷测试的分数) ,其中男生得分处于 C 组的有 14 人,男生 C 组 得分情况分别为:22,22,22,22,22,23,23,23,24,24,24,25,25,25 男生、女
10、生得分的平均数、中位数、众数(单位:分)如表所示: 组别 平均数 中位数 众数 男 20 n 22 女 20 23 20 (1)直接写出 m,n 的值,并补全条形统计图; (2)通过以上数据分析,你认为成绩更好的是男生还是女生?说明理由(一条理由即可) ; (3)已知初三年级总人数为 1800 人,请估计参加问卷测试,成绩处于 C 组的人数 22.根据我们学习函数的过程和方法,对函数 y的图象与性质进行探究 (1)如表是 y 与 x 的几组对应值: x 3.5 3 2 1 0 1 2 3 3.5 y m 2 0 n 2 则 m 的值为 ,n 的值为 (2)描点、连线,在所给的平面直角坐标系中画
11、出该函数的图象,写出该函数的一条性质: (3)若x32xx,结合图象,直接写出 x 的取值范围 23.五一假期即将到来, 重庆是一个集山水、 美食为一体的旅游城市, 重庆某商家在 4 月就进行了 “五一节” 特产促销,已知江津米花糖每盒 12 元,梁平张鸭子每盒 50 元,第一次促销期间,共卖出江津米花糖和 梁平张鸭子共计 2000 盒 (1)若卖出米花糖和鸭子的总销售额不低于 54400 元,则至少卖出梁平张鸭子多少盒? (2) 第一次促销结束, 为了回馈顾客, 在第二次促销期间, 米花糖每盒降价a%, 鸭子每盒降价 4a%, 米花糖数量在(1)问最多的数量下增加 6a%,鸭子数量在(1)问
12、最少的数量下增加 4a%,最终第二次 促销总销售额比第一次促销的最低销售额 54400 元少 80a 元,求 a 的值 24.在数的学习过程中,我们通过对其中一些具有某种特性的数进行研究探索,发现了数字的美和数学的灵 动性,现在我们继续探索一类数 定义:一个各位数字均不为 0 的四位自然数 t,若 t 的百位、十位数字之和的 2 倍等于千位与个位数字之 和,那我们称这个四位数 t 为“优数” 例如:当 t6414 时,2(4+1)(6+4)0,6414 是“优数” ; 当 t4257 时,2(2+5)(4+7)30,4257 不是“优数” (1)判断 1318 和 7401 是否为“优数” ,
13、并说明理由; (2)已知:t(1a9,1b9,1c9 且 a,b,c 均为正整数)是“优数” ,且满足与 的差能被 7 整除,且 F(t)|4+abc|,求 F(t)的最大值 25.如图,在平面直角坐标系中,抛物线 yax2+bx2(a0)与 x 轴交于 A(2,0) ,B(1,0)两点, 与 y 轴交于点 C (1)求抛物线的函数表达式; (2)若点 D 是第三象限内抛物线上一个动点,连接 AC,过点 D 作 DEAC 于点 E,求线段 DE 最大值 及此时点 D 的坐标; (3)将抛物线向右平移 5 个单位得到抛物线 y抛物线 y与抛物线 y 交于点 F,连接 CF,若点 P 是 x 轴上
14、一动点, 是否存在这样的点 P, 使得PCBOCF, 若存在, 请直接写出点 P 的坐标; 若不存在, 请说明理由 四、解答题(本大题 1 个小题,8 分)请把答案写在答题卷上对应的空白处,解答时每小题必 须给出必要的演算过程或推理步骤. 26.在ABC 中,ACBC,D 为ABC 外一点,连接 CD (1)如图 1,若ACB60,CDAB,连接 BD 交 AC 于点 E,且 CD2AB2,求 SBCE (2)如图 2,CECD,ECBDCA,ED 交 AB 于点 F,FG 垂直平分 EC,且 FGEC,M,N 分别为 AF,CD 中点,连接 MN,求证:MNBF (3)如图 3,若ACB90
15、,CDAB,将 AD 绕着 A 点顺时针旋转 60得到 AD,连接 DD,BD, 且 AC,求 BD的最小值 2021 年重庆市沙坪坝区中考数学强化训练试卷(二) 一、选择题: (本大题 12 个小题,每小题 4 分。共 48 分)在每个小题的下面,都给出了代号 为 A,B,C,D 的四个答案。其中只有一个是正确的,请将答题卡上题号右侧正确答案所对 应的方框涂黑。 1.下列数字中最小的数为( ) A2 B1 C0 D 【考点】算术平方根;实数大小比较 【专题】实数;数感 【答案】D 【分析】根据正数比 0 大,负数比 0 小,两个负数相比较,绝对值大的反而小可直接得到答案 【解答】解:由题可得
16、,102, 四个选项中最小的数为, 故选:D 2.由五个小立方体搭成如图的几何体,从正面看到的平面图形是( ) A B C D 【考点】简单组合体的三视图 【专题】应用题 【答案】C 【分析】找到从正面看所得到的图形即可 【解答】解:从正面可看到三列正方形的个数依次为 2,1,1 故选:C 3.估计+2 的值在( ) A0 到 1 之间 B1 到 2 之间 C2 到 3 之间 D3 到 4 之间 【考点】估算无理数的大小 【专题】实数;数感 【答案】D 【分析】先估算的大小,在确定+2 的值在哪两个数之间 【解答】解:12, 3+24, +2 的值在 3 和 4 之间, 故选:D 4.下列计算
17、正确的是( ) Aa3+a3a6 B3aa2 C (a2)3a5 Daa2a3 【考点】合并同类项;同底数幂的乘法;幂的乘方与积的乘方 【专题】常规题型 【答案】D 【分析】直接利用合并同类项法则以及幂的乘方运算法则和同底数幂的乘法运算法则计算得出答案 【解答】解:A、a3+a32a3,故此选项错误; B、3aa2a,故此选项错误; C、 (a2)3a6,故此选项错误; D、aa2a3,故此选项正确; 故选:D 5.下列命题,真命题是( ) A一组对边平行,另一组对边相等的四边形是平行四边形 B有一个角为直角的四边形为矩形 C对角线互相垂直的四边形是菱形 D一组邻边相等的矩形是正方形 【考点】
18、命题与定理 【专题】矩形 菱形 正方形;推理能力 【答案】D 【分析】根据平行四边形的判定定理、矩形、菱形、正方形的判定定理判断即可 【解答】解:A、一组对边平行,另一组对边相等的四边形是平行四边形或梯形,本选项说法是假命题; B、有一个角为直角的平行四边形为矩形,本选项说法是假命题; C、对角线互相垂直的平行四边形是菱形,本选项说法是假命题; D、一组邻边相等的矩形是正方形,本选项说法是真命题; 故选:D 6.孙子算经中有一道题: “今有木,不知长短引绳度之,余绳四尺五,屈绳量之,不足一尺问木长 几何?”译文大致是: “用一根绳子去量一根木条,绳子剩余 4.5 尺;将绳子对折再量木条,木条剩
19、余 1 尺,问木条长多少尺 ”如果设木条长为 x 尺,绳子长为 y 尺,根据题意列方程组正确的是( ) A B C D 【考点】由实际问题抽象出二元一次方程组 【答案】A 【分析】本题的等量关系是:木长+4.5绳长;绳长+1木长,据此可列方程组即可 【解答】解:设木条长为 x 尺,绳子长为 y 尺,根据题意可得, , 故选:A 7.如图,P 是O 外一点,PA 是O 的切线,A 为切点,PO 与O 相交于 B 点,已知BCA34,C 为 O 上一点,连接 CA,CB,则P 的度数为( ) A34 B56 C22 D28 【考点】圆周角定理;切线的性质 【专题】圆的有关概念及性质;运算能力;推理
20、能力 【答案】C 【分析】根据切线的性质和圆周角定理即可求出结果 【解答】解:PA 是O 的切线,A 为切点, OAP90, 又BCA34, O2AOB68, P90AOB906822 故选:C 8.如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比 为,点 A,B,E 在 x 轴上若正方形 ABCD 的边长为 2,则点 F 坐标为( ) A (8,6) B (9,6) C D (10,6) 【考点】坐标与图形性质;位似变换 【专题】图形的相似;符号意识 【答案】B 【分析】直接利用位似图形的性质结合相似比得出 EF 的长,进而得出OBC
21、OEF,进而得出 EO 的 长,即可得出答案 【解答】解:正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为, , BC2, EFBE6, BCEF, OBCOEF, , 解得:OB3, EO9, F 点坐标为: (9,6) , 故选:B 9.一天,小明和朋友一起到小区测量小明所住楼房的高度,他们首先在 A 测得楼房顶部 E 的仰角为 37, 然后沿着斜坡 AB 走了 7.8 米到 B 处,再测得楼房顶部 E 的仰角为 45,身高忽略不计已知斜坡 AB 的坡度 i1:2.4,楼房 EF 所离 BC 高度 CD 为 1.8 米则楼房自身高度 EF 大约为( )米
22、 (参考数据:sin370.60,cos370.80,tan370.75) A40.8 B33.6 C31.8 D30.6 【考点】解直角三角形的应用坡度坡角问题;解直角三角形的应用仰角俯角问题 【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力 【答案】C 【分析】过 A 作 AHBC 交 CB 的延长线于点 H,延长 BC 交 EF 的延长线于点 G,作 AJEF 于点 J, 则 FGCD1.8 米,AHJG,由坡度求出 AH3(米) ,BH7.2(米) ,再证 BGEG,设 BGEG x 米则 HGAJ(x+7.2)米,EJ(x3)米,然后由锐角三角函数定义得0.7
23、5,解得:x 33.6,即可解决问题 【解答】解:过 A 作 AHBC 交 CB 的延长线于点 H,延长 BC 交 EF 的延长线于点 G,作 AJEF 于点 J,如图所示: 则四边形 AHGJ 与四边形 DCGF 都是矩形, FGCD1.8 米,AHJG, 在 RtAHB 中,AB7.8 米, AH3(米) ,BH7.2(米) , EBG45,G90, BGEG, 设 BGEGx 米则 HGAJ(x+7.2)米,EJ(x3)米, 在 RtAEJ 中,tanEAJ0.75, 0.75, 解得:x33.6, 即 EG33.6 米 EFEGFG33.61.831.8(米) , 故选:C 10.已知


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 重庆市 沙坪坝区 中考 数学 强化 训练 试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 沙坪坝区
- 重庆市沙坪坝实验中学
- 2020年重庆市沙坪坝区中考数学综合试卷三含答案
- 2020年重庆市沙坪坝区中考数学综合试卷五含答案
- 2021年重庆市沙坪坝区中考数学适应性试卷含答案详解
- 2021年重庆市北碚区中考数学冲刺试卷含答案解析
- 2021年重庆市中考数学考前押题卷含答案解析
- 2021年重庆市沙坪坝区中考数学强化训练试卷二含答案解析
- 2020年重庆市沙坪坝区中考数学综合试卷六含答案
- 2020年重庆市沙坪坝区中考数学综合试卷一含答案
- 2020年重庆市沙坪坝区中考数学综合试卷四含答案
- 2020年重庆市沙坪坝区中考数学综合试卷二含答案
- 2021年重庆市中考数学预测试卷二含答案解析
- 2021年重庆市合川区中考数学押题试卷二含答案详解
- 2021年重庆市中考预测数学试卷含答案解析
- 重庆市沙坪坝区二校联考
- 重庆市沙坪坝区二校联考2022



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-184130.html