1、2021 年四川省攀枝花市高考数学第二次统一考试试卷（文科）年四川省攀枝花市高考数学第二次统一考试试卷（文科） 一、选择题（共一、选择题（共 12 小题）小题）. 1已知集合 Ax|x2+2x0，Bx|x1，则 AB（ ） A（，2） B（，0）（2，+） C（，1）（0，+） D（，1）（2，+） 2设复数 z 满足（1+i）2z1i（i 为虚数单位），则|z|（ ） A B C D1 3记 Sn为等差数列an的前 n 项和，若 a5+a622，S756，则an的公差为（ ） A1 B2 C4 D8 4过平面 外的直线 l 作一组平面与 相交，若所得交线分别为 a，b，c，则这些交线的位置关
2、系为 （ ） A相交于同一点 B相交但交于不同的点 C平行 D平行或相交于同一点 5甲、乙两人在一次射击比赛中各射靶 5 次，两人成绩的条形统计图如图所示，则（ ） A甲的成绩的平均数小于乙的成绩的平均数 B甲的成绩的中位数等于乙的成绩的中位数 C甲的成绩的方差小于乙的成绩的方差 D甲的成绩的极差小于乙的成绩的极差 6已知 cos+sin（），则 sin（）（ ） A B C D 7党的十九大报告中指出：从 2020 年到 2035 年，在全面建成小康社会的基础上，再奋斗 15 年，基本实 现社会主义现代化若到 2035 年底我国人口数量增长至 14.4 亿，由 2013 年到 2019 年的
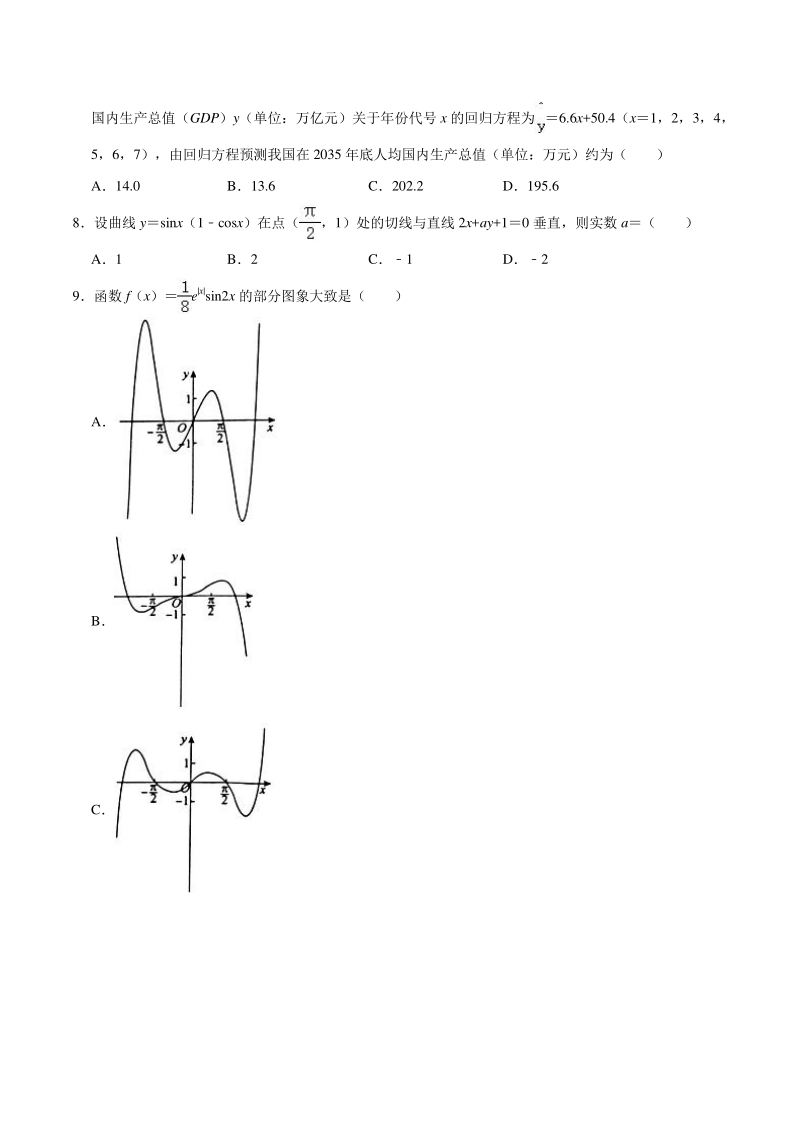
3、统计数据可得 国内生产总值（GDP）y（单位：万亿元）关于年份代号 x 的回归方程为 6.6x+50.4（x1，2，3，4， 5，6，7），由回归方程预测我国在 2035 年底人均国内生产总值（单位：万元）约为（ ） A14.0 B13.6 C202.2 D195.6 8设曲线 ysinx（1cosx）在点（，1）处的切线与直线 2x+ay+10 垂直，则实数 a（ ） A1 B2 C1 D2 9函数 f（x）e|x|sin2x 的部分图象大致是（ ） A B C D 10将函数 ysin（2x+）的图象向右平移个单位长度得到函数 yf（x）的图象，下列说法正确的 是（ ） Af（x）是奇函数
4、 Bf（x）的周期是 Cf（x）的图象关于直线 x对称 Df（x）的图象关于点（，0）对称 11已知函数 f（x）的导函数为 f（x），满足 xf（x）+2f（x），且 f（1）e，已知 a， bln，csin，则（ ） Af（c）f（a）f（b） Bf（a）f（b）f（c） Cf（b）f（a）f（c） Df（c）f（b）f（a） 12在直四棱柱 ABCDA1B1C1D1中，底面 ABCD 是边长为 6 的正方形，点 E 在线段 AD 上，且满足 AE 2ED， 过点E 作直四棱柱 ABCDA1B1C1D1外接球的截面， 所得的截面面积的最大值与最小值之差为 12， 则直四棱柱 ABCDA1B
5、1C1D1外接球的表面积为（ ） A100 B80 C64 D32 二、填空题（共二、填空题（共 4 小题）小题）. 13已知 ， 均为单位向量，且| + |1，则 ， 夹角 的值为 14设变量 x，y 满足约束条件，则 zx+y 的最大值为 15三棱柱 ABCA1B1C1中，侧面与底面垂直，底面是边长为 2 的正三角形，若直线 AB1与 ACC1A1所成的 角为 30，则棱柱的高为 16已知等比数列an的前 n 项和为 Sn，且 Snm25n，则 a1a2an的最大值为 三、解答题：共三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第分。解答应写出文字说明、证明过程或演算步
6、骤。第 1721 题为必考题，每个试题考题为必考题，每个试题考 生都必须作答。第生都必须作答。第 22、23 题为选考题，考生根据要求作答。（一）必考题：共题为选考题，考生根据要求作答。（一）必考题：共 60 分。分。 17已知ABC 的内角 A，B，C 所对的边分别为 a，b，c，且 sin2A+cosA （）求 A； （）若ABC 是锐角三角形，且 b2，求ABC 面积的取值范围 182020 年 3 月，工业和信息化部信息通信发展司发布工业和信息化部关于推动 5G 加快发展的通知， 鼓励基础电信企业通过套餐升级优惠、信用购机等举措，促进 5G 终端消费，加快用户向 5G 迁移为了 落实通
7、知要求，掌握用户升级迁移情况及电信企业服务措施，某市调研部门随机选取了甲、乙两个电信 企业的用户共 165 户作为样本进行满意度调查，并针对企业服务措施设置了达标分数线，按照不低于 80 分的定为满意，低于 80 分的为不满意，调研人员制作了如图所示的 22 列联表 满意 不满意 合计 甲企业用户 75 乙企业用户 20 合计 已知从样本的 165 户中随机抽取 1 户为满意的概率是 （） 请将 22 列联表补充完整， 并判断能否有 95%的把握认为 “满意度与电信企业服务措施有关系” ？ （）为了进一步了解用户对电信企业服务措施不满意的具体情况，调研人员在样本中的甲企业用户中 按照下面的方法
8、抽取一户进行详细调查了解： 把甲企业用户中不满意的户主按 2， 3， 4， 5， 进行编号， 再先后两次抛掷一枚质地均匀的骰子， 出现点数之和为被抽取户主的编号， 且规定点数之和为 12 时抽取 的编号为 2试求抽到 5 号或 10 号的概率 下面临界值表仅供参考： P（K2k0 ） 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828 （参考公式：K2 ，其中 na+b+c+d） 19 如图，ABC 的外接圆 O 的直径 AB2，CE 垂直于圆 O 所在的平面，BDCE， CE
9、2，BCBD1 （）求证：平面 AEC平面 BCED （）若 DMDE，求三棱锥 DACM 的体积 20已知直线 l 经过椭圆 C：1（ab0）的左焦点（c，0）和下顶点，坐标原点 O 到直线 l 的距离为c （）求椭圆 C 的离心率； （）若椭圆 C 经过点 P（2，1），A，B 是椭圆 C 上的两个动点，且APB 的角平分线总是垂直于 y 轴，求证：直线 AB 的斜率为定值 21已知函数 f（x）lnx+a（aR，bR）有最小值 M，且 M0 （）求 ea1b+1 的最大值； （）当 ea1b+1 取得最大值时，设 F（b） m（mR），F（x）有两个零点为 x1，x2（x1x2）， 证明
10、：x1e3 选考题：共选考题：共 10 分。请考生在第分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题记分。题中任选一题作答。如果多做，则按所做的第一题记分。选修选修 4-4： 坐标系与参数方程坐标系与参数方程 22平面直角坐标系 xOy 中，曲线 C 的参数方程为（ 为参数），以坐标原点 O 为极点， 以 x 轴正半轴为极轴建立极坐标系，直线 l 的极坐标方程为2 （）写出曲线 C 的普通方程和直线 l 的直角坐标方程； （）若直线 l 与曲线 C 交于 P，Q 两点，点 M（0，2），求的值 选修选修 4-5：不等式选讲：不等式选讲 23已知函数 f（x）|x+1|
11、+2|x1| （）解不等式 f（x）2x+2； （）设函数 f（x）的最小值为 t，若 a0，b0，且 a+bt，证明：1 参考答案参考答案 一、选择题（共一、选择题（共 12 小题）小题）. 1已知集合 Ax|x2+2x0，Bx|x1，则 AB（ ） A（，2） B（，0）（2，+） C（，1）（0，+） D（，1）（2，+） 解：集合 Ax|x2+2x0 x|x2 或 x0， Bx|x1， ABx|x1 或 x0（，1）（0，+） 故选：C 2设复数 z 满足（1+i）2z1i（i 为虚数单位），则|z|（ ） A B C D1 解：由（1+i）2z1i，得 z， |z| 故选：C 3记
12、Sn为等差数列an的前 n 项和，若 a5+a622，S756，则an的公差为（ ） A1 B2 C4 D8 解：Sn为等差数列an的前 n 项和，a5+a622，S756， ， 解得 a12，d2， an的公差为 2 故选：B 4过平面 外的直线 l 作一组平面与 相交，若所得交线分别为 a，b，c，则这些交线的位置关系为 （ ） A相交于同一点 B相交但交于不同的点 C平行 D平行或相交于同一点 解：当直线与平面平行时， abc，当直线与平面相交时， 设 lO， 则 a、b、c，是过 O 点的直线， 这些交线的位置关系为都平行或都交于同一点 都平行或都交于同一点 故选：D 5甲、乙两人在一
13、次射击比赛中各射靶 5 次，两人成绩的条形统计图如图所示，则（ ） A甲的成绩的平均数小于乙的成绩的平均数 B甲的成绩的中位数等于乙的成绩的中位数 C甲的成绩的方差小于乙的成绩的方差 D甲的成绩的极差小于乙的成绩的极差 解：（4+5+6+7+8）6， （5+5+5+6+9）6， 甲的成绩的方差为（222+122）2， 以的成绩的方差为（123+321）2.4 故选：C 6已知 cos+sin（），则 sin（）（ ） A B C D 解：cos+sin（）cos+sin+cos（cos+sin） sin（+）， 则 sin（）， 故选：A 7党的十九大报告中指出：从 2020 年到 2035
14、年，在全面建成小康社会的基础上，再奋斗 15 年，基本实 现社会主义现代化若到 2035 年底我国人口数量增长至 14.4 亿，由 2013 年到 2019 年的统计数据可得 国内生产总值（GDP）y（单位：万亿元）关于年份代号 x 的回归方程为 6.6x+50.4（x1，2，3，4， 5，6，7），由回归方程预测我国在 2035 年底人均国内生产总值（单位：万元）约为（ ） A14.0 B13.6 C202.2 D195.6 解：到 2035 年底对应的年份代号为 23， 把 x23 代入 6.6x+50.4 得， 6.623+50.4202.2（万亿元）， 又14.0， 所以到 2035
15、年底，我过人均国内生产总值约为 14.0 万元 故选：A 8设曲线 ysinx（1cosx）在点（，1）处的切线与直线 2x+ay+10 垂直，则实数 a（ ） A1 B2 C1 D2 解：ysinx（1cosx）的导数为 f（x）cosx（1cosx）+sin2x， 可得曲线 ysinx（1cosx）在点（，1）处的切线的斜率为 1， 由切线与直线 2x+ay+10 垂直，可得1， 解得 a2， 故选：B 9函数 f（x）e|x|sin2x 的部分图象大致是（ ） A B C D 解：f（x）e| x|sin（2x） e|x|sin2xf（x）， f（x）为奇函数，故排除 D； 当 x时，f
16、（）0，故排除 B； 当 0 x时，f（x）exsin2x， 令 f（x）ex（sin2x+2cos2x）， 设当 xx0时，f（x）0，则 tan2x02， 当 0 xx0时，f（x）0，当 x0 时，f（x）0， 所以 f（x）在（0，x0）上单调递增，在（x0，）上单调递减，f（x0）为（0， ）上的最大值 因为2tan2x0，解得 tanx01+ 或 tanx01（舍）， 又 1+ tan， 所以 x02， f（x0）e|x0|sin2x01， 而 A 选项在（0，）的最大值大于 1，排除 A； 故选：C 10将函数 ysin（2x+）的图象向右平移个单位长度得到函数 yf（x）的图象
17、，下列说法正确的 是（ ） Af（x）是奇函数 Bf（x）的周期是 Cf（x）的图象关于直线 x对称 Df（x）的图象关于点（，0）对称 解：将函数 ysin（2x+）的图象向右平移个单位长度， 得到函数 yf（x）sin（2x+）cos2x 的图象， 故 f（x）是偶函数，最小正周期为，故 A、B 错误； 令 x，求得 f（x），不是最值，故 C 错误； 令 x，求得 f（x）0，故 f（x）的图象关于点（，0）对称，故 D 正确， 故选：D 11已知函数 f（x）的导函数为 f（x），满足 xf（x）+2f（x），且 f（1）e，已知 a， bln，csin，则（ ） Af（c）f（a）f
18、（b） Bf（a）f（b）f（c） Cf（b）f（a）f（c） Df（c）f（b）f（a） 解：xf（x）+2f（x）， x2f（x）+2xf（x）ex， x2f（x）ex，x2f（x）ex+c， 又 f（1）e，则 ee+c，解得：c0， f（x），f（x）， x（0，2）时，f（x）0，f（x）在（0，2）递减， 而 a， blnln且 ln0，0b， csinsin且 sin1，c1， bac， f（b）f（a）f（c）， 故选：A 12在直四棱柱 ABCDA1B1C1D1中，底面 ABCD 是边长为 6 的正方形，点 E 在线段 AD 上，且满足 AE 2ED， 过点E 作直四棱柱 A
19、BCDA1B1C1D1外接球的截面， 所得的截面面积的最大值与最小值之差为 12， 则直四棱柱 ABCDA1B1C1D1外接球的表面积为（ ） A100 B80 C64 D32 解：四棱柱 ABCDA1B1C1D1是直四棱柱，且底面是正方形， 其外接球的球心位于直四棱柱的中心，记作 O，过 O 向底面 ABCD 作垂线，垂足为 G， 则 OGAA1，连接 BD，底面 ABCD 是边长为 6 的正方形，G 为 BD 的中点， 取 AD 的中点 F，连接 OF，OE，OB， 设 AA12a，则 OGa，外接球的半径 ROB 点 E 在线段 AD 上，且满足 AE2ED，则 EFDFDEAB1， 又
20、 FGAB3，OF 直四棱柱中，AB侧面 ADD1A1，FGAB，FG侧面 ADD1A1， FGAD，又 OG底面 ABCD， OGAD，又 FGOGG，AD平面 OFG，则 OFAD 则 OE 根据球的特征，过点 E 作直四棱柱 ABCDA1B1C1D1的外接球的截面， 当截面过球心时，截面面积最大，此时截面面积为 R2， 当 OE 垂直于截面时，此时截面圆的半径为 此时截面面积为 S1（R2OE2） 又截面面积的最大值与最小值之差为 12， SS1R2（R2OE2）OE212， 因此 a2+1012，即 a22，则 R ， 直四棱柱 ABCDA1B1C1D1外接球的表面积为 42080 故
21、选：B 二、填空题：本题共二、填空题：本题共 4 小题，每小题小题，每小题 5 分，共分，共 20 分。分。 13已知 ， 均为单位向量，且| + |1，则 ， 夹角 的值为 120 解： ， 均为单位向量，且| + |1， | + |21，即 2+2+2| | |cos1， cos， 120； 故答案为：120 14设变量 x，y 满足约束条件，则 zx+y 的最大值为 4 解：作出变量 x，y 满足约束条件， 对应的平面区域如图： 变形 zx+y，得 yx+z 平移此直线，由图象可知当直线 yx+z 经过 A 时， 直线在 y 轴的截距最大，得到 z 最大， 由，解得 A（3，1） 所以
22、zx+y 的最大值为 3+14 故答案为：4 15三棱柱 ABCA1B1C1中，侧面与底面垂直，底面是边长为 2 的正三角形，若直线 AB1与 ACC1A1所成的 角为 30，则棱柱的高为 解：取 A1C1中点 D，AC 中点 E，连接 B1D，AD，DE， 侧面与底面垂直，底面是边长为 2 的正三角形， B1D平面 ACC1A1，B1 D，DE 是棱柱的高， B1AD 是直线 AB1与 ACC1A1所成的角， 直线 AB1与 ACC1A1所成的角为 30，DAB130， AB12，AD 3， 棱柱的高 DE2 故答案为：2 16已知等比数列an的前 n 项和为 Sn，且 Snm25n，则 a
23、1a2an的最大值为 1024 解：根据题意，等比数列an中，Snm25n， 当 n2 时，有 anSnSn1（m25n）（m26n） ， 即等比数列an的通项公式为 an， 故当 1n4 时，an1，当 n5 时，an1，当 n6 时，an1， 故当 n4 或 5 时，a1a2an取得最大值，且其最大值为 a1a2a5242322212101024， 故答案为：1024 三、解答题：共三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第分。解答应写出文字说明、证明过程或演算步骤。第 1721 题为必考题，每个试题考题为必考题，每个试题考 生都必须作答。第生都必须作答。第 22
24、、23 题为选考题，考生根据要求作答。（一）必考题：共题为选考题，考生根据要求作答。（一）必考题：共 60 分。分。 17已知ABC 的内角 A，B，C 所对的边分别为 a，b，c，且 sin2A+cosA （）求 A； （）若ABC 是锐角三角形，且 b2，求ABC 面积的取值范围 解：（）由， 可得，即， 可得：， 解得， 由于 0A， 故 （）法一：由题设及（）知ABC 的面积， 由正弦定理得， 由于ABC 为锐角三角形，故， 由（）知，所以，故， 从而，因此，ABC 面积的取值范围是 法二：可以用余弦定理 c 用表示 a，利用锐角三角形两边平方和大于第三边，可以求得 c 的范围 由余弦
25、定理，a2b2+c22bccosA，即 ， 又因为三角形为锐角三角形，此时也满足两边之和大于第三边， 所以，代入可解得， 由题设及（）知ABC 的面积， 从而，因此，ABC 面积的取值范围是 182020 年 3 月，工业和信息化部信息通信发展司发布工业和信息化部关于推动 5G 加快发展的通知， 鼓励基础电信企业通过套餐升级优惠、信用购机等举措，促进 5G 终端消费，加快用户向 5G 迁移为了 落实通知要求，掌握用户升级迁移情况及电信企业服务措施，某市调研部门随机选取了甲、乙两个电信 企业的用户共 165 户作为样本进行满意度调查，并针对企业服务措施设置了达标分数线，按照不低于 80 分的定为
26、满意，低于 80 分的为不满意，调研人员制作了如图所示的 22 列联表 满意 不满意 合计 甲企业用户 75 乙企业用户 20 合计 已知从样本的 165 户中随机抽取 1 户为满意的概率是 （） 请将 22 列联表补充完整， 并判断能否有 95%的把握认为 “满意度与电信企业服务措施有关系” ？ （）为了进一步了解用户对电信企业服务措施不满意的具体情况，调研人员在样本中的甲企业用户中 按照下面的方法抽取一户进行详细调查了解： 把甲企业用户中不满意的户主按 2， 3， 4， 5， 进行编号， 再先后两次抛掷一枚质地均匀的骰子， 出现点数之和为被抽取户主的编号， 且规定点数之和为 12 时抽取
27、的编号为 2试求抽到 5 号或 10 号的概率 下面临界值表仅供参考： P（K2k0 ） 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828 （参考公式：K2 ，其中 na+b+c+d） 解：（）设样本中乙企业用户中满意的有 x 户，结合列联表知， P ，解得 x60； 所以，填写 22 列联表是： 满意 不满意 合计 甲企业用户 75 10 85 乙企业用户 60 20 80 合计 135 30 165 计算 所以能判断有 95%的把握认为“满意度与电信企业服务措施有关系”
28、（）设“抽到 5 号或 10 号”为事件 A，先后两次抛掷一枚骰子，出现的点数为（m，n）， 则所有的基本事件的个数有 6636， 事件 A 包含的基本事件个数（m+n5 或 m+n10）有： （1，4），（2，3），（3，2），（4，1），（4，6），（5，5），（6，4）共有 7 个 所以所求事件的概率为 19 如图，ABC 的外接圆 O 的直径 AB2，CE 垂直于圆 O 所在的平面，BDCE， CE2，BCBD1 （）求证：平面 AEC平面 BCED （）若 DMDE，求三棱锥 DACM 的体积 解：（）证明：因为 AB 为ABC 的外接圆 O 的直径， 所以 ACBC， 又因为 EC
29、平面 ABC，所以 ECBC， 又 ACECC， 所以 BC平面 ACE，又 BC平面 BCED， 所以平面 AEC平面 BCDE （）因为，所以， 因为平面 AEC平面 BCDE， 过 M 作 MN 垂直于 CE，交 CE 于 N， 则 MN 为锥体的高且，AC， 所以 20已知直线 l 经过椭圆 C：1（ab0）的左焦点（c，0）和下顶点，坐标原点 O 到直线 l 的距离为c （）求椭圆 C 的离心率； （）若椭圆 C 经过点 P（2，1），A，B 是椭圆 C 上的两个动点，且APB 的角平分线总是垂直于 y 轴，求证：直线 AB 的斜率为定值 解：（）法一：过点（c，0），（0，b）的直
30、线 l 的方程为 bx+cy+bc01 分 则坐标原点 O 到直线 l 的距离为 2 分 可得4 分 法二：由三角形等面积法可知： 2 分 可得4 分 （）由（）易知，则椭圆 C：经过点 P（2，1）， 解得 b23，则椭圆 C： 5 分 法一：因为APB 的角平分线总垂直于 y 轴，所以 AP 与 BP 所在直线关于直线 y1 对称 设直线 AP 的斜率为 k，则直线 BP 的斜率为k 所以设直线 AP 的方程为 y1k（x2）， 直线 BP 的方程为 y1k（x2）， 设点 A（x1，y1），B（x2，y2）6 分 由，消去 y，得（1+2k2）x2+4（k2k2）x+8k28k40 因为
31、点 P（2，1）在椭圆 C 上，则有，即8 分 同理可得9 分 所以，又11 分 所以直线 AB 的斜率为12 分 法二：设直线 AB 的方程为 ykx+t，点 A（x1，y1），B（x2，y2），则 y1kx1+t，y1kx2+t， 直线 AP 的斜率，直线 BP 的斜率 因为APB 的角平分线总垂直于 y 轴，所以 AP 与 BP 所在直线关于直线 y1 对称 所以 kAPkBP，即 6 分 化简得 x1y2+x2y1（x1+x2）2（y1+y2）+40 把 y1kx1+t，y1kx2+t，代入上式，并化简得 2kx1x2+（t12k）（x 1+x2）4t+407 分 由由，消去 y，得（
32、1+2k2）x2+4ktx+2t260 则， 代入化简得9 分 整理得 2k23k+1+ktt0（k1）（t+2k1）0 所以 k1 或 t+2k1010 分 若 t12k，可得方程（1+2k2）x2+4ktx+2t260 的一个根为 2，不合题意 11 分 当 k1 时，合题意 所以直线 AB 的斜率为12 分 法三：设点 A（x1，y1），B（x2，y2），则直线 AP 的斜率 ，直线 BP 的斜率 因为APB 的角平分线总垂直于 y 轴，所以 AP 与 BP 所在直线关于直线 y1 对称 所以 kAPkBP，即 6 分 因为点 A（x1，y1），B（x2，y2） 在椭圆 C 上，所以，
33、则有， 同理有8 分 从而有9 分 由 两式相减得 x1+x22（y1+y2）10 分 又因为11 分 所以直线 AB 的斜率为12 分 21已知函数 f（x）lnx+a（aR，bR）有最小值 M，且 M0 （）求 ea1b+1 的最大值； （）当 ea1b+1 取得最大值时，设 F（b） m（mR），F（x）有两个零点为 x1，x2（x1x2）， 证明：x1e3 解：（）有题意 f（x）（x0）， 当 b0 时，f（x）0，f（x）在（0，+）上单增，此时显然不成立， 当 b0 时，令 f（x）0，得 xb， 此时 f（x）在（0，b）上单减，在（b，+）上单增， Mf（b）lnb+1a0，
34、即 lnba1，所以 bea1，ea1b0 所以 ea1b+1 的最大值为 1 （）证明：当 ea1b+1 取得最大值时，a1lnb， ， F（x）的两个零点为 x1，x2，则，即 lnx1mx1，lnx2mx2， 不等式恒成立等价于 lnx1+2lnx2mx1+2mx2m（x1+2x2）3， 两式相减得， 带入上式得， 令，则，g（t）0， 所以函数 g（t）在（0，1）上单调递增，g（t）g（1）0，得证 选考题：共选考题：共 10 分。请考生在第分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题记分。题中任选一题作答。如果多做，则按所做的第一题记分。选修选修 4-4
35、： 坐标系与参数方程坐标系与参数方程 22平面直角坐标系 xOy 中，曲线 C 的参数方程为（ 为参数），以坐标原点 O 为极点， 以 x 轴正半轴为极轴建立极坐标系，直线 l 的极坐标方程为2 （）写出曲线 C 的普通方程和直线 l 的直角坐标方程； （）若直线 l 与曲线 C 交于 P，Q 两点，点 M（0，2），求的值 解：（）曲线 C 的参数方程为， 消去参数 得曲线 C 的普通方程 y2x2 ， cos+sin20 又 cosx，siny 直线 l 的直角坐标方程为 x+y20 （）法一：设直线 l 的参数方程为（t 为参数， 将其代入曲线 C 的直角坐标方程化简得， 法二：由， 化
36、简得 2x2+x20， 则， 从而， 选修选修 4-5：不等式选讲：不等式选讲 23已知函数 f（x）|x+1|+2|x1| （）解不等式 f（x）2x+2； （）设函数 f（x）的最小值为 t，若 a0，b0，且 a+bt，证明：1 【解答】（）解：不等式等价于或或， 解得 x或或 1x3 所以不等式 f（x）2x+2 的解集为 （）证明：法一：由知，当 x1 时，f（x）minf（1）2， 即 a+b2 法二：f（x）|x+1|+2|x1|（|x+1|+|x1|）+|x1|x+1x+1|+|11|2， 当且仅当 x1 时，取得等号，则 f（x）的最小值为 2，即 a+b2 法一： 当且仅当 ab1，不等式取得等号，所以 法二：所以 ， 当且仅当 ab1，不等式取得等号，所以 法三：由柯西不等式可得： 当且仅当 ab1，不等式取得等号，所以
