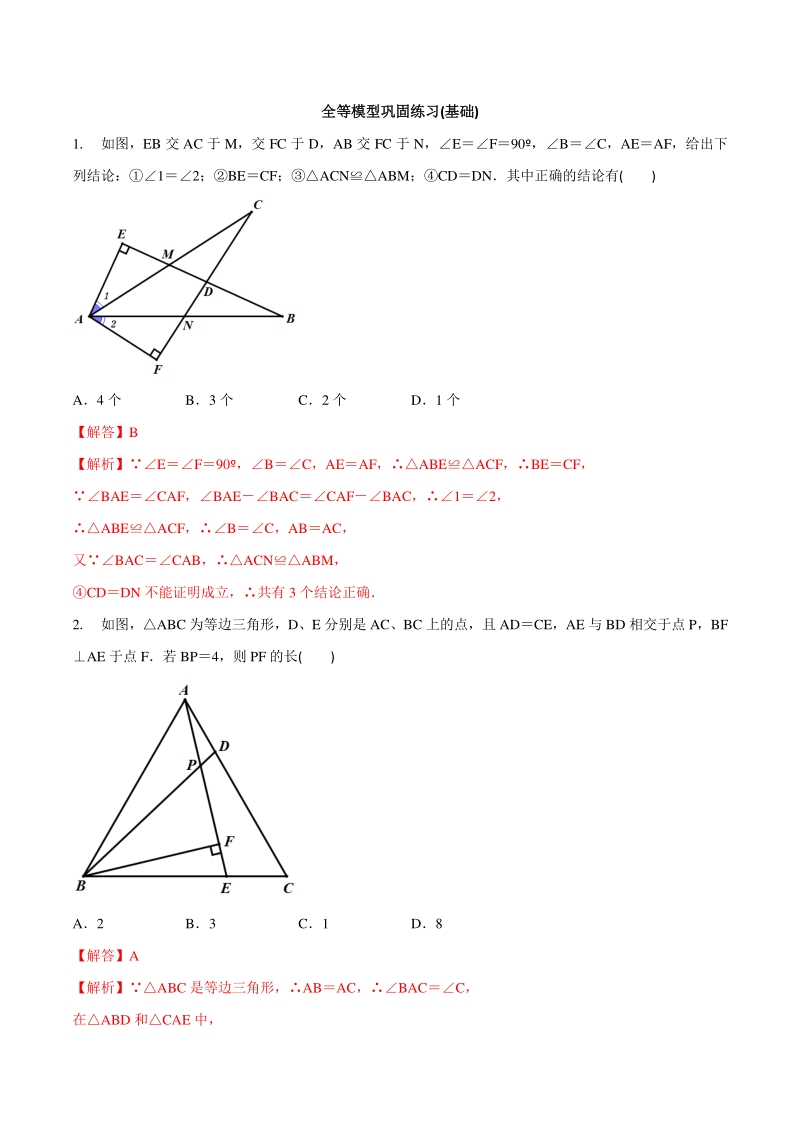
1、 全等模型巩固练习全等模型巩固练习(基础基础) 1. 如图，EB 交 AC 于 M，交 FC 于 D，AB 交 FC 于 N，EF90，BC，AEAF，给出下 列结论：12；BECF；ACNABM；CDDN其中正确的结论有( ) A4 个 B3 个 C2 个 D1 个 【解答】B 【解析】EF90，BC，AEAF，ABEACF，BECF， BAECAF，BAEBACCAFBAC，12， ABEACF，BC，ABAC， 又BACCAB，ACNABM， CDDN 不能证明成立，共有 3 个结论正确 2. 如图，ABC 为等边三角形，D、E 分别是 AC、BC 上的点，且 ADCE，AE 与 BD
2、相交于点 P，BF AE 于点 F若 BP4，则 PF 的长( ) A2 B3 C1 D8 【解答】A 【解析】ABC 是等边三角形，ABAC，BACC， 在ABD 和CAE 中， ，ABDCAE(SAS)， ABDCAE，APDABPPABBAC60，BPFAPD60， BFP90，BPF60，PBF30，PF2. 3. 如图，四边形 ABCD 中，对角线 AC、BD 交于点 O，ABAC，点 E 是 BD 上一点，且 AEAD， EADBAC (1)求证：ABDACD； (2)若ACB65，求BDC 的度数 【解答】(1)见解析；(2)50 【解析】(1)证明：BACEAD，BACEACE
3、ADEAC，即BAECAD， 在ABE 和ACD 中，ABEACD ，ABDACD ； (2)BOC 是ABO 和DCO 的外角，BOCABDBAC，BOCACDBDC， ABDBACACDBDC， ABDACD，BACBDC ， ACB65，ABAC，ABCACB65 ， BAC180ABCACB180656550 ，BDCBAC50 4. 已知：在ABC 中，ABAC，D 为 AC 的中点，DEAB，DFBC，垂足分别为点 E，F，且 DE DF求证：ABC 是等边三角形 【解答】见解析 【解析】证明：DEAB，DFBC，垂足分别为点 E，F，AEDCFD90， D 为 AC 的中点，AD
4、DC， 在 RtADE 和 RtCDF 中，ADDC，DEDF，RtADERtCDF， AC，BABC，ABAC，ABBCAC，ABC 是等边三角形 5. 已知，在ABC 中，A90，ABAC，点 D 为 BC 的中点 (1)如图 1，若点 E、F 分别为 AB、AC 上的点，且 DEDF，求证：BEAF； (2)若点 E、F 分别为 AB、CA 延长线上的点，且 DEDF，那么 BEAF 吗？请利用图 2 说明理由 【解答】(1)见解析；(2)见解析 【解析】(1)证明：连接 AD，如图所示， A90，ABAC，ABC 为等腰直角三角形，EBD45， 点 D 为 BC 的中点，ADBCBD，
5、FAD45， BDEEDA90，EDAADF90，BDEADF， 在BDE 和ADF 中，BDEADF(ASA)，BEAF； (2)BEAF，证明如下： 连接 AD，如图所示 ABDBAD45，EBDFAD135 EDBBDF90，BDFFDA90，EDBFDA 在EDB 和FDA 中，EDBFDA(ASA)，BEAF 6. 如图，ABC 和ADE 分别是以 BC，DE 为底边且顶角相等的等腰三角形，点 D 在线段 BC 上，AF 平分 DE 交 BC 于点 F，连接 BE，EF (1)CD 与 BE 相等？若相等，请证明；若不相等，请说明理由； (2)若BAC90，求证：BF2CD2FD2
6、【解答】(1)CDBE；(2)见解析 【解析】(1)CDBE，理由如下： ABC 和ADE 为等腰三角形，ABAC，ADAE， EADBAC，EADBADBACBAD，即EABCAD， 在EAB 与CAD 中EABCAD，BECD， (2)BAC90，ABC 和ADE 都是等腰直角三角形，ABFC45， EABCAD，EBAC，EBA45，EBF90， 在 RtBFE 中，BF2BE2EF2， AF 平分 DE，AF 垂直平分 DE，EFFD， 由(1)可知，BECD，BF2CD2FD2. 7. (1)如图 1，已知：在ABC 中，BAC90，ABAC，直线 m 经过点 A，BD直线 m，CE
7、直线 m，垂足分别为点 D、E证明：DEBDCE (2)如图 2，将(1)中的条件改为：在ABC 中，ABAC，D、A、E 三点都在直线 m 上，并且有BDA AECBAC， 其中 为任意锐角或钝角 请问结论 DEBDCE 是否成立？如成立， 请你给出证明； 若不成立，请说明理由 【解答】(1)见解析；(2)成立，理由见解析 (1)证明：BD直线 m，CE直线 m，BDACEA90， BAC90，BADCAE90， BADABD90，CAEABD， 在ADB 和CEA 中， ，ADBCEA(AAS)， AEBD，ADCE，DEAEADBDCE； (2)成立 BDABAC，DBABADBADCAE180，CAEABD， 在ADB 和CEA 中 ，ADBCEA(AAS)， AEBD，ADCE，DEAEADBDCE.
