1、2021 年江苏省南通市海安市十校联考中考数学模拟试卷（年江苏省南通市海安市十校联考中考数学模拟试卷（3 月份）月份） 一、选择题（本大题共有一、选择题（本大题共有 10 小题，每小题小题，每小题 3 分，共分，共 30 分在每小题所给出的四个选项中，恰有一项是符分在每小题所给出的四个选项中，恰有一项是符 合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上） 1下列各数中，比2 小的数是（ ） A0 B C|6| D4 22020 年新型冠状型病毒肺炎病在全球蔓延，给人们的生产生活带来巨大影响，截止到 2021 年元月美国
2、 新型冠状型病毒肺炎确诊病例超过 2100 万例，用科学记数法表示正确的是（ ） A21106例 B0.21108例 C2.1106例 D2.1107例 3 分 别 从 正 面 、 上 面 、 左 面 观 察 下 列 物 体 ， 得 到 的 平 面 图 形 完 全 相 同 的 是 （ ） A B C D 4下列运算中，结果正确的是（ ） A （a+b）2a2+b2 B C （a1） （a+1）a21 Da6a2a3 5若关于 x 的一元一次方程 2kx40 的解是 x3，那么 k 的值是（ ） A B C6 D10 6将一把直尺和一块含 30角的三角板 ABC 按如图所示的位置放置，如果CED
3、46，那么BAF 的 度数为（ ） A48 B16 C14 D32 7若菱形的两条对角线长分别是 6 和 8，则它的周长为（ ） A20 B24 C40 D48 8 如图是某个球放进盒子内的截面图， 球的一部分露出盒子外， 已知O 交矩形 ABCD 的边 AD 于点 E， F， 已知 ABEF2，则球的半径长为（ ） A B C D 9 如图， 两个全等的矩形 AEFG， 矩形 ABCD 如图所示放置 CD 所在直线与 AE， GF 分别交于点 H， M 若 AB3，BC，CHMH则线段 MH 的长度是（ ） A B C D2 10如图 1，在菱形 ABCD 中，A120，点 E 是 BC 边
4、的中点，点 P 是对角线 BD 上一动点，设 PD 的 长度为 x，PE 与 PC 的长度和为 y，图 2 是 y 关于 x 的函数图象，其中 H 是图象上的最低点，则 a+b 的 值为（ ） A B C D 二、填空题（本大题共二、填空题（本大题共 8 小题，第小题，第 1112 题每小题题每小题 3 分，第分，第 1318 题每小题题每小题 3 分，共分，共 30 分不需写出解分不需写出解 答过程，请把答案直接填写在答题卡相应位置上）答过程，请把答案直接填写在答题卡相应位置上） 11抛物线 y2（x+1）23 的顶点坐标为 12设 a，b 是方程 x2x20220 的两个实数根，则 a22
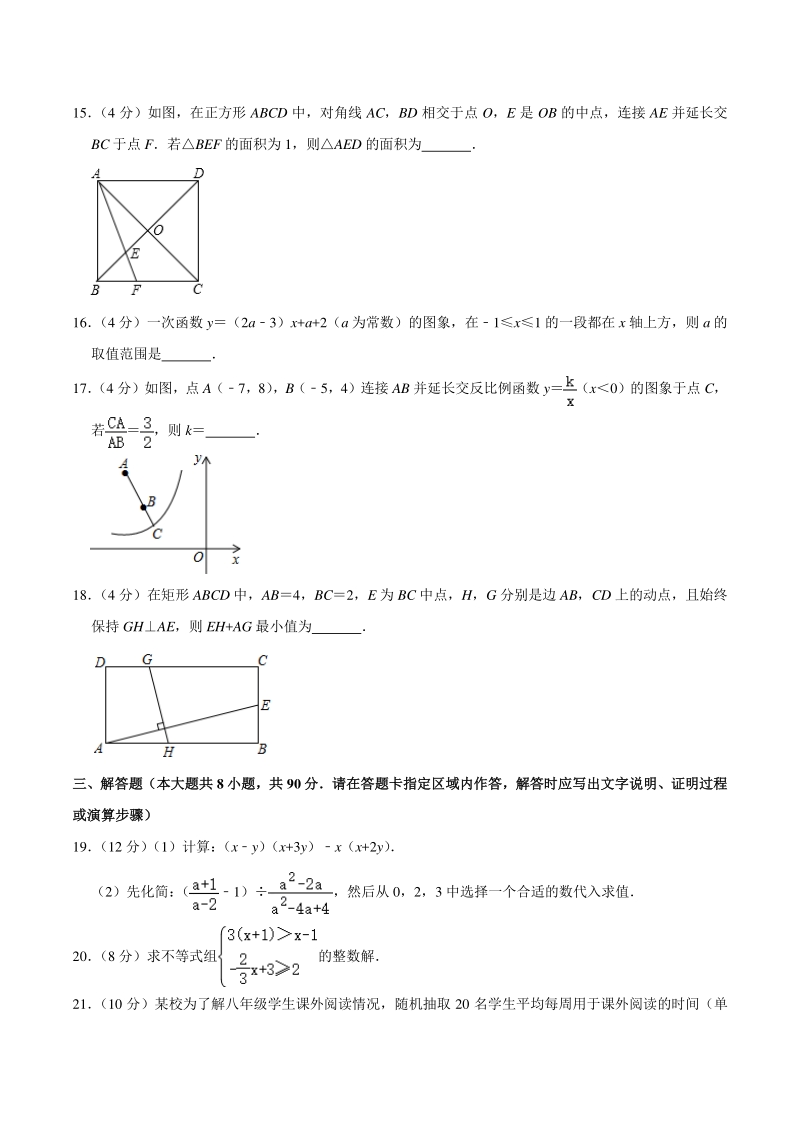
5、ab 的值为 13 （4 分）已知圆锥的侧面积是 40，底面圆直径为 2，则圆锥的母线长是 14 （4 分）中国清代数学著作御制数理精蕴中有这样一道题： “马四匹、牛六头，共价四十八两（ “两” 是我国古代货币单位） ；马三匹、牛五头，共价三十八两则马每匹价 两 15 （4 分）如图，在正方形 ABCD 中，对角线 AC，BD 相交于点 O，E 是 OB 的中点，连接 AE 并延长交 BC 于点 F若BEF 的面积为 1，则AED 的面积为 16 （4 分）一次函数 y（2a3）x+a+2（a 为常数）的图象，在1x1 的一段都在 x 轴上方，则 a 的 取值范围是 17 （4 分）如图，点
6、A（7，8） ，B（5，4）连接 AB 并延长交反比例函数 y（x0）的图象于点 C， 若，则 k 18 （4 分）在矩形 ABCD 中，AB4，BC2，E 为 BC 中点，H，G 分别是边 AB，CD 上的动点，且始终 保持 GHAE，则 EH+AG 最小值为 三、解答题（本大题共三、解答题（本大题共 8 小题，共小题，共 90 分请在答题卡指定区域内作答，解答时应写出文字说明、证明过程分请在答题卡指定区域内作答，解答时应写出文字说明、证明过程 或演算步骤）或演算步骤） 19 （12 分） （1）计算： （xy） （x+3y）x（x+2y） （2）先化简： （1），然后从 0，2，3 中选择
7、一个合适的数代入求值 20 （8 分）求不等式组的整数解 21 （10 分）某校为了解八年级学生课外阅读情况，随机抽取 20 名学生平均每周用于课外阅读的时间（单 位：min） ，过程如表 【收集数据】 30 60 81 50 40 110 130 146 90 100 60 81 120 140 70 81 10 20 100 81 【整理数据】 课外阅读时间 x （min） 0 x40 40 x80 80 x120 120 x160 等级 D C B A 人数 3 a 8 b 【分析数据】 平均数 中位数 众数 80 m n 请根据以上提供的信息，解答下列问题： （1）填空：a ，b ，m
8、 ，n ； （2）如果每周用于课外阅读的时间不少于 80min 为达标，该校八年级现有学生 800 人，估计八年级达标 的学生有多少人？ 22 （10 分）已知有一个 30 度的角，两个 45 度的角，一个 60 度的角 （1）从中任取两个角，请用树状图或列表求出两个角恰好互余的概率； （2）已知在 RtABC 中，C90，BC2，A 是上面四个角中的一个，求边 AB 的长 23 （12 分）如图，已知O 的直径 AB 垂直弦 CD 于点 E，过 C 点作 CGAD 交 AB 延长线于点 G，连接 CO 并延长交 AD 于点 F，且 CFAD （1）求证：CG 是O 的切线； （2）若 AB4
9、，求 CD 的长 24 （12 分）在平面直角坐标系 xOy 中，二次函数 yax2+bx+c 的图象经过点 A（0，4）和 B（2，2） （1）求 c 的值，并用含 a 的式子表示 b； （2）直线 AB 上有一点 C（m，5） ，将点 C 向右平移 4 个单位长度，得到点 D，若抛物线与线段 CD 只 有一个公共点，求 a 的取值范围 25 （13 分）如图 1，矩形 ABCD 中，已知 AB6BC8，点 E 是射线 BC 上的一个动点，连接 AE 并延 长，交射线 DC 于点 F将ABE 沿直线 AE 翻折，点 B 的对应点为点 B，延长 AB交 CD 于点 M （1）如图 1，若点 E
10、 为线段 BC 的中点，求证：AMFM； （2）如图 2，若点 B恰好落在对角线 AC 上，求的值； （3）若，求线段 AM 的长 26 （13 分）在平面直角坐标系 xOy 中，对于ABC，点 P 在 BC 边的垂直平分线上，若以点 P 为圆心，PB 为半径的P 与ABC 三条边的公共点个数之和不小于 3， 则称点 P 为ABC 关于边 BC 的 “Math 点” 如 图所示，点 P 即为ABC 关于边 BC 的“Math 点” 已知点 P（0，4） ，Q（a，0） （1）如图 1，a4，在点 A（1，0） 、B（2，2） 、C（，） 、D（5，5）中，POQ 关于边 PQ 的“Math 点
11、”为 （2）如图 2， 已知 D（0，8） ，点 E 为POQ 关于边 PQ 的“Math 点” ，请直接写出线段 DE 的长度的取值范围； 将POQ 绕原点 O 旋转一周，直线交 x 轴、y 轴于点 M、N，若线段 MN 上存在POQ 关 于边 PQ 的“Math 点” ，求 b 的取值范围 2021 年江苏省南通市海安市十校联考中考数学模拟试卷（年江苏省南通市海安市十校联考中考数学模拟试卷（3 月份）月份） 参考答案与试题解析参考答案与试题解析 一、选择题（本大题共有一、选择题（本大题共有 10 小题，每小题小题，每小题 3 分，共分，共 30 分在每小题所给出的四个选项中，恰有一项是符分
12、在每小题所给出的四个选项中，恰有一项是符 合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上） 1下列各数中，比2 小的数是（ ） A0 B C|6| D4 【分析】根据有理数的大小比较解答即可 【解答】解：因为420|6|， 故选：D 22020 年新型冠状型病毒肺炎病在全球蔓延，给人们的生产生活带来巨大影响，截止到 2021 年元月美国 新型冠状型病毒肺炎确诊病例超过 2100 万例，用科学记数法表示正确的是（ ） A21106例 B0.21108例 C2.1106例 D2.1107例 【分析】科学记数法的表示形式为
13、a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把 原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值10 时，n 是正整数；当原数的绝对值1 时，n 是负整数 【解答】解：2100 万210000002.1107 故选：D 3 分 别 从 正 面 、 上 面 、 左 面 观 察 下 列 物 体 ， 得 到 的 平 面 图 形 完 全 相 同 的 是 （ ） A B C D 【分析】图、图、图、图可以近似的看作正方体，圆锥体，长方体、圆柱体，根据它们三视 图的形状进行判断即可 【解答】解：图、图、图、图可以近似的看作正方体，圆锥体，长方体、
14、圆柱体， 正方体的三视图都是正方形的， 圆锥体的主视图、左视图是三角形的，而俯视图是圆形的， 长方体的三视图虽然都是长方形的，但它们的大小不相同， 圆柱的主视图、主视图是长方形的，但俯视图是圆形的， 因此从正面、上面、左面看所得到的平面图形完全相同的是正方体， 故选：A 4下列运算中，结果正确的是（ ） A （a+b）2a2+b2 B C （a1） （a+1）a21 Da6a2a3 【分析】直接利用二次根式的加减运算法则、完全平方公式、平方差公式分别计算得出答案 【解答】解：A、 （a+b）2a2+2ab+b2，故此选项错误； B、+，故此选项错误； C、 （a1） （a+1）a21，故此选项
15、正确； D、a6a2a4，故此选项错误； 故选：C 5若关于 x 的一元一次方程 2kx40 的解是 x3，那么 k 的值是（ ） A B C6 D10 【分析】把 x3 代入方程得出 2k+340，再求出 k 即可 【解答】解：关于 x 的一元一次方程 2kx40 的解是 x3， 2k+340， 解得：k， 故选：A 6将一把直尺和一块含 30角的三角板 ABC 按如图所示的位置放置，如果CED46，那么BAF 的 度数为（ ） A48 B16 C14 D32 【分析】根据平行线的性质和三角板的角度解答即可 【解答】解：DEAF， CEDEAF46， BAC903060， BAFBACEAF
16、604614， 故选：C 7若菱形的两条对角线长分别是 6 和 8，则它的周长为（ ） A20 B24 C40 D48 【分析】根据菱形的对角线互相垂直平分的性质，利用对角线的一半，根据勾股定理求出菱形的边长， 再根据菱形的四条边相等求出周长即可 【解答】解：如图所示， 根据题意得 AO84，BO63， 四边形 ABCD 是菱形， ABBCCDDA，ACBD， AOB 是直角三角形， AB5， 此菱形的周长为：5420 故选：A 8 如图是某个球放进盒子内的截面图， 球的一部分露出盒子外， 已知O 交矩形 ABCD 的边 AD 于点 E， F， 已知 ABEF2，则球的半径长为（ ） A B
17、C D 【分析】由题意得O 与 BC 相切，记切点为 G，作直线 OG，分别交 AD、劣弧于点 H、I，连接 OF， 易求得 FH 的长，设O 的半径为 r，则 OH2r，然后在 RtOFH 中，由勾股定理得 r2（2r）2 12，解此方程即可求得答案 【解答】解：由题意得：O 与 BC 相切，记切点为 G，作直线 OG，分别交 AD、劣弧于点 H、I，连 接 OF，如图所示： 四边形 ABCD 是矩形， ADBC， IGBC， IGAD， FHEF1， 设O 的半径为 r，则 OH2r， 在 RtOFH 中，由勾股定理得：r2（2r）212， 解得：r， 即球的半径长为， 故选：C 9 如图
18、， 两个全等的矩形 AEFG， 矩形 ABCD 如图所示放置 CD 所在直线与 AE， GF 分别交于点 H， M 若 AB3，BC，CHMH则线段 MH 的长度是（ ） A B C D2 【分析】作 HKFG 于 K则四边形 EFKH 是矩形利用全等三角形的寻找证明 AHMHCH，设 CH AHx，根据勾股定理构建方程即可解决问题； 【解答】解：作 HKFG 于 K则四边形 EFKH 是矩形 MHK+AHD90，AHD+DAH90， MHKDAH， HKMADH，KHEFAD， HKMADH， MHAH， CHMH， AHCH，设 AHCHx， 在 RtADH 中，x23+（3x）2， 解得
19、 x2， MH2， 故选：D 10如图 1，在菱形 ABCD 中，A120，点 E 是 BC 边的中点，点 P 是对角线 BD 上一动点，设 PD 的 长度为 x，PE 与 PC 的长度和为 y，图 2 是 y 关于 x 的函数图象，其中 H 是图象上的最低点，则 a+b 的 值为（ ） A B C D 【分析】由 A、C 关于 BD 对称，推出 PAPC，推出 PC+PEPA+PE，推出当 A、P、E 共线时，PE+PC 的值最小，观察图象可知，当点 P 与 B 重合时，PE+PC6，推出 BECE2，ABBC4，分别求出 PE+PC 的最小值，PD 的长即可解决问题 【解答】解：在菱形 A
20、BCD 中，A120，点 E 是 BC 边的中点， 易证 AEBC， A、C 关于 BD 对称， PAPC， PC+PEPA+PE， 当 A、P、E 共线时，PE+PC 的值最小，即 AE 的长 观察图象可知，当点 P 与 B 重合时，PE+PC6， BECE2，ABBC4， 在 RtAEB 中，AE2， PC+PE 的最小值为 2， 点 H 的纵坐标 a2， BCAD， 2， BD4， PD， 点 H 的横坐标 b， a+b2+； 故选：C 二、填空题（本大题共二、填空题（本大题共 8 小题，第小题，第 1112 题每小题题每小题 3 分，第分，第 1318 题每小题题每小题 3 分，共分，
21、共 30 分不需写出解分不需写出解 答过程，请把答案直接填写在答题卡相应位置上）答过程，请把答案直接填写在答题卡相应位置上） 11抛物线 y2（x+1）23 的顶点坐标为 （1，3） 【分析】直接利用顶点式的特点可知顶点坐标 【解答】解：顶点坐标是（1，3） 故答案为： （1，3） 12设 a，b 是方程 x2x20220 的两个实数根，则 a22ab 的值为 2021 【分析】根据一元二次方程的解及根与系数的关系可得出 a2a2022、a+b1，将其代入 a22ab （a2a）（a+b）中即可求出结论 【解答】解：a，b 是方程 x2x20220 的两个实数根， a2a2022，a+b1，
22、a22ab（a2a）（a+b）202212021 故答案为：2021 13 （4 分）已知圆锥的侧面积是 40，底面圆直径为 2，则圆锥的母线长是 40 【分析】圆锥的侧面积底面周长母线长2，把相应数值代入即可求解 【解答】解：设母线长为 R，底面圆直径为 2，则底面周长2，圆锥的侧面积2R40，R 40 14 （4 分）中国清代数学著作御制数理精蕴中有这样一道题： “马四匹、牛六头，共价四十八两（ “两” 是我国古代货币单位） ；马三匹、牛五头，共价三十八两则马每匹价 6 两 【分析】设马每匹价 x 两，牛每头价 y 两，根据“马四匹、牛六头，共价四十八两；马三匹、牛五头， 共价三十八两”
23、，即可得出关于 x，y 的二元一次方程组，解之即可得出结论 【解答】解：设马每匹价 x 两，牛每头价 y 两， 依题意，得：， 解得： 故答案为：6 15 （4 分）如图，在正方形 ABCD 中，对角线 AC，BD 相交于点 O，E 是 OB 的中点，连接 AE 并延长交 BC 于点 F若BEF 的面积为 1，则AED 的面积为 9 【分析】根据正方形的性质得 OBOD，ADBC，根据三角形相似的性质和判定得：，根 据同高三角形面积的比等于对应底边的比，可得结论 【解答】解：四边形 ABCD 是正方形， OBOD，ADBC， BEFDEA， ， E 是 OB 的中点， ， ， ， BEF 的面
24、积为 1， AEB 的面积为 3， ， ， AED 的面积为 9， 故答案为：9 16 （4 分）一次函数 y（2a3）x+a+2（a 为常数）的图象，在1x1 的一段都在 x 轴上方，则 a 的 取值范围是 a5 或a 【分析】根据一次函数 y（2a3）x+a+2 的图象在1x1 的一段都在 x 轴的上方，由一次函数的 性质，则有 2a30，再分 2a30 和 2a30 来讨论，解得即可 【解答】解：因为 y（2a3）x+a+2 是一次函数， 所以 2a30，a， 当 2a30 时，y 随 x 的增大而增大，由 x1 得：y2a+3+a+2， 根据函数的图象在 x 轴的上方，则有2a+3+a
25、+20， 解得：a5 当 2a30 时，y 随 x 的增大而减小，由 x1 得：y2a3+a+2，根据函数的图象在 x轴的上方， 则有：2a3+a+20，解得：a， 故答案为：a5 或a 17 （4 分）如图，点 A（7，8） ，B（5，4）连接 AB 并延长交反比例函数 y（x0）的图象于点 C， 若，则 k 8 【分析】作 ADx 轴于 D，BEx 轴于 E，CFx 轴于 F，根据平行线分线段成比例定理求出点 C 的坐 标，代入反比例函数解析式计算即可 【解答】解：作 ADx 轴于 D，BEx 轴于 E，CFx 轴于 F， 则 ADBECF， ， ， ， ， 点 A（7，8） ，B（5，4
26、） ， DE2， EF1， OF4，即点 C 的横坐标为4， 同理，点 C 的纵坐标为 2，即点 C 的坐标为（4，2） ， 点 C 在反比例函数 y（x0）的图象上， k428， 故答案为：8 18 （4 分）在矩形 ABCD 中，AB4，BC2，E 为 BC 中点，H，G 分别是边 AB，CD 上的动点，且始终 保持 GHAE，则 EH+AG 最小值为 【分析】过 G 作 GNAB 于 N，依据ABEGNH，即可得到 GH 的长；以 AG，AE 为邻边作平行四 边形 AEMG，可得 AG+HEME+HE，当 H，E，M 在同一直线上时，AG+HE 的最小值等于 HM 的长， 再根据勾股定理
27、求得 HM 的长，即可得到 EH+AG 的最小值 【解答】解：如图所示，过 G 作 GNAB 于 N，则ANG90，GNAD2， GHAE， ANGAFG90， BAENGH， ABEGNH， ， RtABE 中，AE， ， GH， 如图所示，以 AG，AE 为邻边作平行四边形 AEMG，则 AGME，GMAE，HGMAFG 90， AG+HEME+HE， 当 H，E，M 在同一直线上时，AG+HE 的最小值等于 HM 的长， 此时，RtGHM 中，HM， EH+AG 的最小值为， 故答案为 三、解答题（本大题共三、解答题（本大题共 8 小题，共小题，共 90 分请在答题卡指定区域内作答，解答
28、时应写出文字说明、证明过程分请在答题卡指定区域内作答，解答时应写出文字说明、证明过程 或演算步骤）或演算步骤） 19 （12 分） （1）计算： （xy） （x+3y）x（x+2y） （2）先化简： （1），然后从 0，2，3 中选择一个合适的数代入求值 【分析】 （1）根据多项式乘以多项式、单项式乘以多项式的计算方法进行计算即可； （2）先根据分式混合运算的法则把原式进行化简，再选取合适的 x 的值代入进行计算即可 【解答】解： （1） （xy） （x+3y）x（x+2y） x2+3xyxy3y2x22xy 3y2； （2）解：原式（） ， a0，a2 时，原式没有意义， 当 a3 时，原式
29、1 20 （8 分）求不等式组的整数解 【分析】先求出不等式组的解集，再求其整数解即可 【解答】解： 解不等式得：x2； 解不等式得：x； 所以不等式组的解集为2x 整数解为：1，0，1 21 （10 分）某校为了解八年级学生课外阅读情况，随机抽取 20 名学生平均每周用于课外阅读的时间（单 位：min） ，过程如表 【收集数据】 30 60 81 50 40 110 130 146 90 100 60 81 120 140 70 81 10 20 100 81 【整理数据】 课外阅读时间 x （min） 0 x40 40 x80 80 x120 120 x160 等级 D C B A 人数
30、3 a 8 b 【分析数据】 平均数 中位数 众数 80 m n 请根据以上提供的信息，解答下列问题： （1）填空：a 5 ，b 4 ，m 81 ，n 81 ； （2）如果每周用于课外阅读的时间不少于 80min 为达标，该校八年级现有学生 800 人，估计八年级达标 的学生有多少人？ 【分析】 （1）根据统计表收集数据可求 a，b，再根据中位数、众数的定义可求 m，n； （2）达标的学生人数总人数达标率，依此即可求解 【解答】解： （1）由统计表收集数据可知 a5，b4，m81，n81 故答案为：5，4，81，81； （2）800480（人） 所以估计八年级达标的学生有 480 人 22 （
31、10 分）已知有一个 30 度的角，两个 45 度的角，一个 60 度的角 （1）从中任取两个角，请用树状图或列表求出两个角恰好互余的概率； （2）已知在 RtABC 中，C90，BC2，A 是上面四个角中的一个，求边 AB 的长 【分析】 （1） 列表得出所有等可能结果， 从中找到两个角恰好互余的结果数， 再根据概率公式求解即可； （2）分A30、45、60三种情况，根据 AB分别计算即可 【解答】解： （1）列表如下： 30 45 45 60 30 75 75 90 45 75 90 105 45 75 90 105 60 90 105 105 由表知，共有 12 种等可能结果，其中两个角
32、恰好互余的有 4 种结果， 两个角恰好互余的概率为； （2）若A30， 在 RtABC 中，BC2， AB2BC4； 若A45， 在 RtABC 中，BC2， AB2； 若A60， 在 RtABC 中，BC2， AB 23 （12 分）如图，已知O 的直径 AB 垂直弦 CD 于点 E，过 C 点作 CGAD 交 AB 延长线于点 G，连接 CO 并延长交 AD 于点 F，且 CFAD （1）求证：CG 是O 的切线； （2）若 AB4，求 CD 的长 【分析】 （1）已知点 C 在O 上，由平行线的性质可得FCG90，由切线的判定定理可得答案； （2）连接 BD，先证明 CFBD，从而BDE
33、OCE，根据相似三角形的性质列出比例式，结合垂径 定理可得 BEOE，在 RtCOE 中，由勾股定理解得 CE，再乘以 2 即可 【解答】解： （1）CFAD， AFC90， CGAD， FCG90， OCCG， CG 是O 的切线； （2）连接 BD，如图， AB 为O 的直径， ADB90， 又CFA90， ADBCFA， CFBD， BDEOCE， ， AECD，且 AE 过圆心 O， DECE， BEOE， AB4， OCOB2， OEBE1， 在 RtCOE 中，由勾股定理得： CE， CD2CE CD 的长为 24 （12 分）在平面直角坐标系 xOy 中，二次函数 yax2+bx
34、+c 的图象经过点 A（0，4）和 B（2，2） （1）求 c 的值，并用含 a 的式子表示 b； （2）直线 AB 上有一点 C（m，5） ，将点 C 向右平移 4 个单位长度，得到点 D，若抛物线与线段 CD 只 有一个公共点，求 a 的取值范围 【分析】 （1）把点 A（0，4）和 B（2，2）分别代入 yax2+bx+c，即可求解； （2） 当 a0 时， 若抛物线与线段 CD 只有一个公共点， 则抛物线上的点 （1， 3a7） 在 D 点的下方， 即可求解；当 a0 时，若抛物线的顶点在线段 CD 上，则抛物线与线段只有一个公共点，即可求解 【解答】解： （1）把点 A（0，4）和
35、B（2，2）分别代入 yax2+bx+c 中，得 c4，4a2b+c2 b2a3； （2）设直线 AB 的表达式为：ymx+n，则，解得：， 故直线 AB 表达式为 y3x4，把 C（m，5）代入得 m3 C（3，5） ， 由平移得 D（1，5） 当 a0 时，若抛物线与线段 CD 只有一个公共点（如图 1） ， yax2+bx+cax2+（2a3）x4，当 x1 时，y3a7， 则抛物线上的点（1，3a7）在 D 点的下方， a+2a345 解得 a4 0a4； 当 a0 时，若抛物线的顶点在线段 CD 上， 则抛物线与线段只有一个公共点（如图 2） ， 5即5 解得 a3+（舍去）或 a3
36、 综上，a 的取值范围是 0a4 或 a3 25 （13 分）如图 1，矩形 ABCD 中，已知 AB6BC8，点 E 是射线 BC 上的一个动点，连接 AE 并延 长，交射线 DC 于点 F将ABE 沿直线 AE 翻折，点 B 的对应点为点 B，延长 AB交 CD 于点 M （1）如图 1，若点 E 为线段 BC 的中点，求证：AMFM； （2）如图 2，若点 B恰好落在对角线 AC 上，求的值； （3）若，求线段 AM 的长 【分析】 （1）由折叠的性质及等腰三角形的判定可得出答案； （2）由勾股定理求出 AC10，证明ABEFCE，由比例线段可得出答案； （3） 分两种情况讨论： 点 E
37、 在线段 BC 上， 点 E 在 BC 的延长线上， 分别设 DMx， 根据 RtADM 中，AM2AD2+DM2，得到关于 x 的方程，求得 x 的值即可 【解答】 （1）证明：四边形 ABCD 为矩形， ABCD， FBAF， 由折叠可知：BAFMAF， FMAF， AMFM （2）解：由（1）可知ACF 是等腰三角形，ACCF， 在 RtABC 中，AB6，BC8， AC10， CFAC10， ABCF， ABEFCE， ； （3）当点 E 在线段 BC 上时，如图 3，AB的延长线交 CD 于点 M， 由 ABCF 可得：ABEFCE， ，即， CF4， 由（1）可知 AMFM 设 D
38、Mx，则 MC6x，则 AMFM10 x， 在 RtADM 中，AM2AD2+DM2，即（10 x）282+x2， 解得：x， AM10 x10 当点 E 在 BC 的延长线上时，如图 4， 由 ABCF 可得：ABEFCE， ，即， CF4， 则 DF642， 设 DMx，则 AMFM2+x， 在 RtADM 中，AM2AD2+DM2，即（2+x）282+x2， 解得：x15， AM2+x17 综上所述：当时，AM 的长为或 17 26 （13 分）在平面直角坐标系 xOy 中，对于ABC，点 P 在 BC 边的垂直平分线上，若以点 P 为圆心，PB 为半径的P 与ABC 三条边的公共点个数
39、之和不小于 3， 则称点 P 为ABC 关于边 BC 的 “Math 点” 如 图所示，点 P 即为ABC 关于边 BC 的“Math 点” 已知点 P（0，4） ，Q（a，0） （1）如图 1，a4，在点 A（1，0） 、B（2，2） 、C（，） 、D（5，5）中，POQ 关于边 PQ 的“Math 点”为 B，C （2）如图 2， 已知 D（0，8） ，点 E 为POQ 关于边 PQ 的“Math 点” ，请直接写出线段 DE 的长度的取值范围； 将POQ 绕原点 O 旋转一周，直线交 x 轴、y 轴于点 M、N，若线段 MN 上存在POQ 关 于边 PQ 的“Math 点” ，求 b 的
40、取值范围 【分析】 （1）根据“Math 点”的定义，结合图象判断即可 （2） 首先证明PQO30， 当点 E 与 PQ 的中点 K 重合时， 点 E 是POQ 关于边 PQ 的 “Math 点” ， 此时 E（2，2） ，当E与 x 轴相切于点 Q 时，E（4，8） ，推出 DE4，观察图象可知， 当点 E 在线段 KE上时，点 E 为POQ 关于边 PQ 的“Math 点” ，求出点 D 到直线 EK 的最小值， 即可解决问题 如图 3 中， 分别以 O 为圆心， 4 和 4为半径画圆， 当线段 MN 与图中圆环 （包括小圆， 不包据大圆） 有交点时，线段 MN 上存在POQ 关于边 PQ
41、 的“Math 点” ，求出直线 MN 与大圆相切或小圆交于（4， 0）或（4，0）时 b 的值，即可判断 【解答】解： （1）根据“Math 点”的定义，观察图象可知，POQ 关于边 PQ 的“Math 点”为 B、C 故答案为：B，C （2）如图 2 中，P（0，4） ，Q（4，0） ， OP4，OQ4， tanPQO， PQO30， 当点 E 与 PQ 的中点 K 重合时，点 E 是POQ 关于边 PQ 的“Math 点” ，此时 E（2，2） ， D（0，8） ， DE4， 当E与 x 轴相切于点 Q 时，E（4，8） ， DE4， 观察图象可知，当点 E 在线段 KE上时，点 E 为POQ 关于边 PQ 的“Math 点” ， EQOQ， EQO90， EQK60， EKQ90， EEQ30， DEOQ， DEK60， DEDK， DEK 是等边三角形， 点 D 到 EK 的距离的最小值为 4sin606， 如图 3 中，分别以 O 为圆心，4 和 4为半径画圆， 当线段 MN 与图中圆环 （包括小圆， 不包据大圆） 有交点时， 线段 MN 上存在POQ 关于边 PQ 的 “Math 点” ， 当直线 MN 与小圆交于（4，0）或（4，0）时，b， 当直线 MN 与大圆相切时，b8， 观察图象可知，满足条件的 b 的值为：b8或8b
