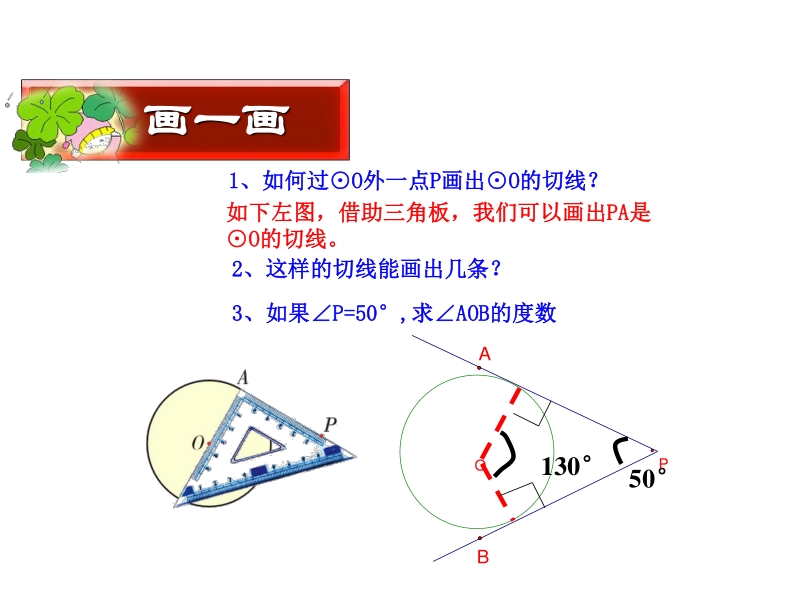
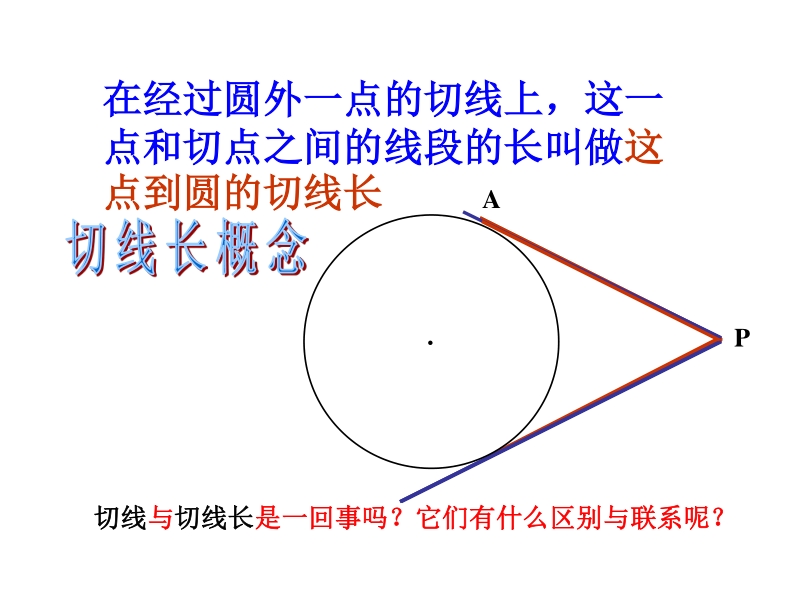
1、 50 OP B A 1 1、如何过、如何过O O外一点外一点P P画出画出O O的切线？的切线？ 2 2、这样的切线能画出几条？、这样的切线能画出几条？ 如下左图，借助三角板，我们可以画出如下左图，借助三角板，我们可以画出PAPA是是 O O的切线。的切线。 3 3、如果、如果P=50P=50, ,求求AOBAOB的度数的度数 130 画一画画一画 在经过圆外一点的切线上，这一在经过圆外一点的切线上，这一 点和切点之间的线段的长叫做点和切点之间的线段的长叫做这这 点到圆的切线长点到圆的切线长 O P A B 切线切线与与切线长切线长是一回事吗？是一回事吗？它们有什么区别与联系呢？它们有什么区
2、别与联系呢？ 切线和切线长是两个不同的概念：切线和切线长是两个不同的概念： 1、切线是一条与圆相切的、切线是一条与圆相切的直线直线， 不能度量；不能度量； 2、切线长是、切线长是线段线段的长，这条线段的长，这条线段 的两个端点分别是圆外一点和切的两个端点分别是圆外一点和切 点，可以度量。点，可以度量。 O P A B O A B P 思考思考:已知已知O切线切线PA、PB，A、B为切为切 点，把圆沿着直线点，把圆沿着直线OP对折对折,你能发现什么你能发现什么? 1 2 请证明你所发现的结论。请证明你所发现的结论。 A P O B PA = PB OPA=OPB 证明：证明：PAPA，PBPB与
3、与O O相切，点相切，点A A，B B是切点是切点 OAPAOAPA，OBPBOBPB 即即OAP=OBP=90 OA=OB，OP=OP RtRtAOPRtAOPRtBOP(HL)BOP(HL) PA = PB OPA=OPB 试用文字语言试用文字语言 叙述你所发现叙述你所发现 的结论的结论 PA、PB分别切分别切O于于A、B PA = PB OPA=OPB 从圆外一点引圆的从圆外一点引圆的 两条切线，它们的切两条切线，它们的切 线长相等，圆心和这线长相等，圆心和这 一点的连线平分两条一点的连线平分两条 切线的夹角。切线的夹角。 几何语言几何语言: 反思：反思：切线长定理为证明线段相等、角相等
4、提切线长定理为证明线段相等、角相等提 供新的方法供新的方法 O P A B A P O B 若连结两切点若连结两切点A A、B B，ABAB交交 OPOP于点于点M.M.你又能得出什么新的你又能得出什么新的 结论结论? ?并给出证明并给出证明. . OP垂直平分垂直平分AB 证明：证明：PAPA，PBPB是是O O的切线的切线, ,点点A A，B B是切点是切点 PA = PB OPA=OPB PABPAB是等腰三角形是等腰三角形，PMPM为为顶角顶角的平分线的平分线 OP垂直平分垂直平分AB M A P O 。 B 若延长若延长PO交交O于点于点C，连结，连结CA、CB，你又能得出什么新的你
5、又能得出什么新的 结论结论? ?并给出证明并给出证明. . CA=CB 证明：证明：PAPA，PBPB是是O O的切线的切线, ,点点A A，B B是切点是切点 PA = PB OPA=OPB PC=PCPC=PC PCA PCB AC=BCAC=BC C 。 P B A O （3）连结圆心和圆外一点）连结圆心和圆外一点 （2）连结两切点）连结两切点 （1）分别连结圆心和切点）分别连结圆心和切点 反思：在解决有 关圆的切线长问 题时，往往需要 我们构建基本图 形。 （2）已知OA=3cm,OP=6cm，则APB= P A B C O _ （4）OP交O于M,则 , M 牛刀小试牛刀小试 （3）
6、若P=70，则AOB= _ （1）若PA=4、PM=2，求圆O的半径OA 已知：如图已知：如图,PA,PA、PBPB是是O O的切线，切点分别的切线，切点分别 是是A A、B B，Q Q为为ABAB上一点，过上一点，过Q Q点作点作O O的切线，的切线， 交交PAPA、PBPB于于E E、F F点，已知点，已知PA=12CMPA=12CM，求，求PEFPEF 的周长。的周长。 E A Q P F B O 易证易证EQ=EA, FQ=FB,PA=PBEQ=EA, FQ=FB,PA=PB PE+EQ=PA=12cm PF+FQ=PB=PA=12cm 周长为24cm 例例1 1、已知：、已知：P P
7、为为O O外一点，外一点，PAPA、PBPB为为O O的切线，的切线， A A、B B为切点，为切点，BCBC是直径。是直径。 求证：求证：ACOPACOP P A C B D O 例题讲解例题讲解 例例1 1、已知：、已知：P P为为O O外一点，外一点，PAPA、PBPB为为O O的的 切线，切线，A A、B B为切点，为切点，BCBC是直径。是直径。 求证：求证：ACOPACOP P A C B O 例题讲解例题讲解 练习练习1.（口答）如图所示（口答）如图所示PA、PB分别切圆分别切圆O于于A、 B，并与圆，并与圆O的切线分别相交于的切线分别相交于C、D，已知，已知 PA=7cm， (
8、1)求求PCD的周长的周长 (2) 如果如果P=46,求求COD的度数的度数 C O P B D A E 例例2 2 、如图，四边形、如图，四边形ABCDABCD的边的边 ABAB、BCBC、CDCD、 DADA和圆和圆O O分别相切于点分别相切于点L L、M M、 N N、P P， 求证：求证： AD+BC=AB+CDAD+BC=AB+CD D L M N A B C O P 证明：由切线长定理得证明：由切线长定理得 AL=APAL=AP，LB=MB,NC=MCLB=MB,NC=MC， DN=DPDN=DP AL+LB+NC+DN=AP+MB+MC+DPAL+LB+NC+DN=AP+MB+M
9、C+DP 即即 AB+CD=AD+BCAB+CD=AD+BC 补充：圆的外切四边形的两组对边的和相等补充：圆的外切四边形的两组对边的和相等 例例3.如图，如图，ABC 中中,C =90 ,它的内切它的内切 圆圆O分别与边分别与边AB、BC、 CA相切于点相切于点D、E、F， 且且BD=12,AD=8， 求求O的半径的半径r. O E B D C A F 练习练习2.如图，如图，AB是是O的直径，的直径，AD、DC、 BC是切线，点是切线，点A、E、B为切点，为切点， (1)求证：求证：OD OC (2)若若BC=9，AD=4，求，求OB的长的长. O A B C D E O A B C D E
10、 F O A B C D E 选做题：如图，选做题：如图，AB是是O的直径，的直径， AD、DC、BC是切线，点是切线，点A、E、B 为切点，若为切点，若BC=9，AD=4，求，求OE的长的长. 1.切线长定理切线长定理 从圆外一点引圆的两条切线从圆外一点引圆的两条切线,它们的切它们的切 线长相等，圆心和这一点的连线平分两条切线的夹线长相等，圆心和这一点的连线平分两条切线的夹 角。角。 PA、PB分别切分别切O于于A、B PA = PB ,OPA=OPB OP垂直平分垂直平分AB 切线长定理为证明切线长定理为证明线段相等，角相等，弧相等，垂线段相等，角相等，弧相等，垂 直关系直关系提供了理论依
11、据。必须掌握并能灵活应用。提供了理论依据。必须掌握并能灵活应用。 课堂小结课堂小结课堂小结课堂小结课堂小结课堂小结课堂小结课堂小结 2.我们学过的切线，常有我们学过的切线，常有 性质：性质： (1)(1)切线和圆只有一个公共点；切线和圆只有一个公共点； (2)(2)切线和圆心的距离等于圆的半径；切线和圆心的距离等于圆的半径； (3)(3)切线垂直于过切点的半径；切线垂直于过切点的半径； (4)(4)经过圆心垂直于切线的直线必过切点；经过圆心垂直于切线的直线必过切点； (5)(5)经过切点垂直于切线的直线必过圆心。经过切点垂直于切线的直线必过圆心。 (6)(6)从圆外一点引圆的两条切线，它们的切线长从圆外一点引圆的两条切线，它们的切线长 相等，圆心和这一点的连线平分两条切线的夹角。相等，圆心和这一点的连线平分两条切线的夹角。 六个六个
