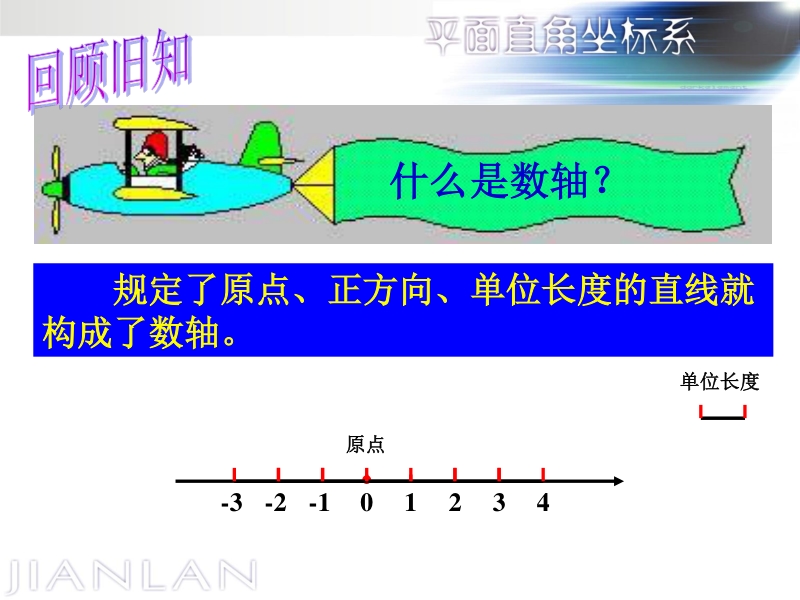
1、笛卡尔笛卡尔 什么是数轴？什么是数轴？ 规定了原点、正方向、单位长度的直线就规定了原点、正方向、单位长度的直线就 构成了数轴。构成了数轴。 单位长度单位长度 0 1 2 3 4 -3 -2 -1 原点原点 数轴上的点数轴上的点A表示数表示数1. 我们说数我们说数1是点是点A在数轴在数轴 上的坐标。上的坐标。 数轴上的点与数轴上的点与 _之间存在着之间存在着 一一对应的关系。一一对应的关系。 实数 同理可知，同理可知， 点点B在数轴上的坐标是在数轴上的坐标是-3； 点点C在数轴上的坐标是在数轴上的坐标是 ； 点点D在数轴上坐标是在数轴上坐标是0. 5 5 0 1 B D A C 问题问题1: 1
2、:车站正东车站正东100100米处有一所学校米处有一所学校, ,正西正西 5050米处是少年宫米处是少年宫, ,请问能否在一条数轴上请问能否在一条数轴上 表示出这三者的位置表示出这三者的位置? ?为什么为什么? ? 问题问题2:2:如果车站正北如果车站正北150150米处有一个图书米处有一个图书 馆馆, ,你能在上述的数轴中同时表示这四者你能在上述的数轴中同时表示这四者 的位置吗的位置吗? ?为什么为什么? ? 据说有一天，笛卡尔生据说有一天，笛卡尔生 病卧床，病情很重，尽病卧床，病情很重，尽 管如此，他还是在思考管如此，他还是在思考 一个百思不得其解的题一个百思不得其解的题 有没有一种方法可
3、有没有一种方法可 以确定事物的位置？突以确定事物的位置？突 然，他看见屋顶上的一然，他看见屋顶上的一 只苍蝇粘在蜘蛛网上，只苍蝇粘在蜘蛛网上， 这时蜘蛛迅速地顺着丝这时蜘蛛迅速地顺着丝 爬上去捉住苍蝇，接着在爬上去捉住苍蝇，接着在 网里上、下、左、右不网里上、下、左、右不 停地运动，笛卡尔恍然停地运动，笛卡尔恍然 大悟大悟“啊，可以像蜘蛛一啊，可以像蜘蛛一 样用网格来确定事物样用网格来确定事物 的位置的位置”。 y x 1 2 3 4 5 6 -1 -2 -3 -4 -5 1 2 3 4 5 6 -1 -2 -3 -4 -5 o 定义：定义： 在平面内画两条互相垂直，并且有公共原点在平面内画两
4、条互相垂直，并且有公共原点O 的数轴的数轴,组成平面直角坐标系组成平面直角坐标系 这个平面叫坐标平面这个平面叫坐标平面 纵轴纵轴 横轴横轴 横轴和纵轴横轴和纵轴 统称为坐标轴统称为坐标轴 坐标原点坐标原点 x 横轴横轴 y 纵轴纵轴 原点原点 第第一一象限象限 第第四四象限象限 第第三三象限象限 第第二二象限象限 注注 意意: :坐标轴上的点不属于任何象限。坐标轴上的点不属于任何象限。 M o 1 2 3 4 5 -4 -3 -2 -1 3 1 4 2 -2 -4 -1 -3 x 0 1 2 3 4 5 -1 -2 -3 -4 -5 -6 -7 7 6 y 1 2 3 4 5 -1 -2 -3
5、 -4 -5 -6 . A (-3, 横坐标横坐标 纵坐标纵坐标 A A点在点在x x轴上的坐标为轴上的坐标为- -3 3 A A点在点在y y轴上的坐标为轴上的坐标为- -4 4 有序数对有序数对( (- -3,3,- -4) 4) 叫做叫做A A点在平面直角坐标系中的坐标点在平面直角坐标系中的坐标 -4) (0,-3) C 由点写坐标：由点写坐标： B E (-5,0) F (4,3.5) y轴上的点的横坐标都为轴上的点的横坐标都为0 x轴上的点的纵坐标都为轴上的点的纵坐标都为0 ( ) -4, -3 平面直角坐标系，平面直角坐标系， 两条数轴来唱戏。两条数轴来唱戏。 一个点，两个数，一个
6、点，两个数， 先横后纵再括号，先横后纵再括号， 最后逗号来隔开。最后逗号来隔开。 例例 写出平面直角坐标系中的写出平面直角坐标系中的、 、OO、T T各点的坐标各点的坐标. . 0 1 2 3 4 5 6 6 5 4 3 2 1 y x -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 A B C O E H G T F 由点写坐标：由点写坐标： 例例 写出平面直角坐标系中的写出平面直角坐标系中的、 、OO、T T各点的坐标各点的坐标. . (4,3.5) (-4,4.5) (-4,-3) (2,-1) (-3,-4) (0,0) (-5,0) (0,-3) 观察你所求出
7、的这些点的观察你所求出的这些点的 坐标坐标, ,回答下列问题回答下列问题: : (1)(1)这些点分别位于哪个象这些点分别位于哪个象 限或坐标轴限或坐标轴? ? (2)(2)请仔细观察你所写出请仔细观察你所写出 的这些点的横、纵坐标的的这些点的横、纵坐标的 符号符号, ,在表中归纳在四个在表中归纳在四个 象限内的点的横、纵坐标象限内的点的横、纵坐标 各有什么特征各有什么特征? ? (0,2.5) 0 1 2 3 4 5 6 6 5 4 3 2 1 y x -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 A B C O E H G T F x 横轴横轴 y 纵轴纵轴 原点
8、原点 第第一一象限象限 第第四象限象限 第第三三象限象限 第第二二象限象限 （，）（，） （，）（，） （，）（，） （，）（，） 点的位置点的位置 在第一象限在第一象限 横坐标横坐标 符号符号 在第二象限在第二象限 在第三象限在第三象限 在第四象限在第四象限 + + + + + + - - - - + + - - - - 纵坐标纵坐标 符号符号 探索探索:根据点所在根据点所在 的位置的位置,用用 “+” “- -” 填空。填空。 -4 o 1 2 3 4 -3 -2 -1 3 1 4 2 -2 -4 -1 -3 (1)在平面直角坐标系中画出点在平面直角坐标系中画出点M(5,3)、A 、 C(
9、-4.5,0)、D(0,-4)、H 、B(0,4) 、 E F . . 0 1 2 3 4 5 6 6 5 4 3 2 1 y x -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 O M(,) D 由坐标描点：由坐标描点： )2, 0(A )2, 0( )5, 2( )5, 2(H )2, 0( )5, 2( C B E F 例例2 2 （2）请用彩色）请用彩色 笔和直尺将其笔和直尺将其 中七个点按照中七个点按照 ABCD EFHA的的 顺序依次连接顺序依次连接 起来；起来； （3）请为你的）请为你的 作品画出点睛作品画出点睛 之笔，并写出之笔，并写出 该点该点R的坐标
10、的坐标. -1 -2 -3 -4 -5 -6 0 1 2 3 4 5 6 4 3 2 1 y -6 -5 -4 -3 -2 -1 x B E F A C D R(-3,0) H M 5 6 （1）在点）在点A（-2，-4）、）、B（-2，4）、）、C（3，-4）、）、 D（3，4） 、 E（-1，0）、）、 F（0，8）、）、G（2，-4）、）、 H （0，-5）中属于第三象限的点是）中属于第三象限的点是 ，属于第四象，属于第四象 限的是限的是 ，在，在X轴上的点是轴上的点是 ，在，在Y轴上的点是轴上的点是 。 例例3 （2）已知点）已知点A（2a-8，3+2a）在第二象限，求）在第二象限，求
11、a的取值的取值 范围范围 应用新知应用新知 知识梳理知识梳理 1、能够正确画出直角坐标系。、能够正确画出直角坐标系。 2、能在直角坐标系中，根据坐标找出点，、能在直角坐标系中，根据坐标找出点， 由点求出坐标由点求出坐标. 3、掌握各个象限内点、掌握各个象限内点、x轴，轴，y轴上点的坐标的特点。轴上点的坐标的特点。 第一象限第一象限 （，）（，） 第二象限第二象限 （，）（，） 第三象限第三象限 （，）（，） 第四象限第四象限 （，）（，） x轴上的点的纵坐标为轴上的点的纵坐标为0，表示为（，表示为（x，0） y轴上的点的横坐标为轴上的点的横坐标为0，表示为（，表示为（0，y) 练一练练一练 一
12、、课本第一、课本第121页“作业页“作业1、2、3、4、5”。 二二、补充练习：补充练习： 1.下列点中下列点中，位于第二象限的是位于第二象限的是（ ） A.（2，-3） B.（-2，-3） C. （-2，3） D. （2，3） 2.如点如点(2m,m-4)在第四象限在第四象限,且且m为偶数为偶数, 则则m= 。 3 . 若点若点A（x,y）的坐标满足）的坐标满足xy=0，则点，则点A在（在（ ） 上上 A.原点原点 B.x轴轴 C.y轴轴 D.x轴或轴或y轴轴 C D 2 挑战自我挑战自我 5.5.在点在点M M（- -1 1，0 0）、）、N N（0 0，- -1 1）、）、P P（- -
13、2 2，- -1 1）、）、O O（5 5， 0 0）、）、R R（0 0，- -5 5）、）、S S（- -3 3，2 2）中，在中，在x x轴上的点的个轴上的点的个 数是（数是（ ） A A、1 B1 B、2 C2 C、3 D3 D、4 4 6.6.如果如果xyxy0 0，且，且x xy y0 0，那么，那么p p（x,yx,y）在（在（ ） A A 、第一象限、第一象限 B B、第二象限、第二象限 C C、第三象限、第三象限 D D、第四象限、第四象限 B B C C y x A O 3 2 -3 -1 B C D 4、指出、指出A、B、C、D各点的各点的 坐标坐标 1.1.在点在点M
14、M（- -1 1，0 0）、）、N N（0 0，- -1 1）、）、P P（- -2 2，- -1 1）、）、O O（5 5， 0 0）、）、R R（0 0，- -5 5）、）、S S（- -3 3，2 2）中，在中，在x x轴上的点的轴上的点的 个数是（个数是（ ） A A、1 B1 B、2 C2 C、3 D3 D、4 4 2.2.如果如果xyxy0 0，且，且x xy y0 0，那么，那么p p（x,yx,y）在（在（ ） A A 、第一象限、第一象限 B B、第二象限、第二象限 C C、第三象限、第三象限 D D、第四象限、第四象限 3.3.若点若点A A（x,yx,y）的坐标满足）的坐标满足xy=0,xy=0,则点则点A A在（在（ ）上）上 A A、原点、原点 B B、x x轴轴 C C、 y y轴轴 D D、 x x轴或轴或y y轴轴 D D B B C C 若点若点C （ 2a-4,5-a ）在第四象限，则）在第四象限，则a的取值范围是什么的取值范围是什么? 变式一变式一:若点若点 C在第二象限在第二象限,则则a的取值范围是什么的取值范围是什么? 变式二变式二:若点若点 C在在y轴上轴上,则则a的取值是什么的取值是什么? 谢谢大家！
