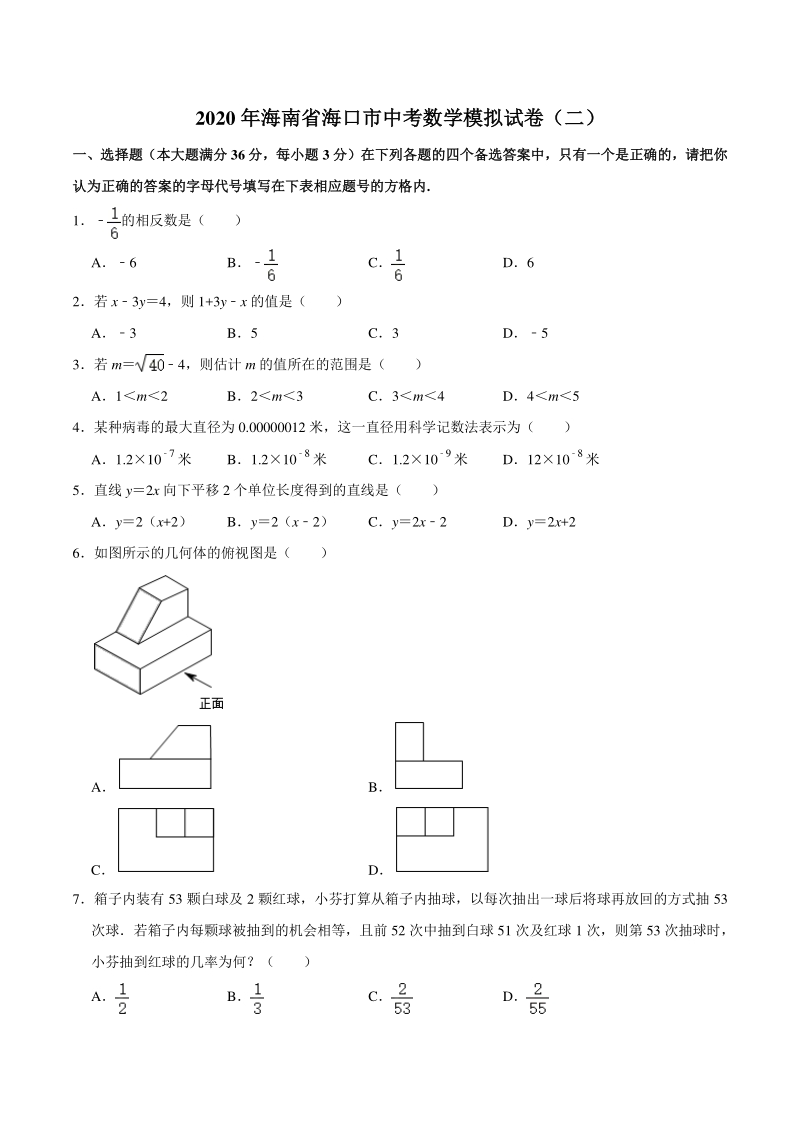
1、2020 年海南省海口市中考数学模拟试卷（二）年海南省海口市中考数学模拟试卷（二） 一、选择题（本大题满分一、选择题（本大题满分 36 分，每小题分，每小题 3 分）在下列各题的四个备选答案中，只有一个是正确的，请把你分）在下列各题的四个备选答案中，只有一个是正确的，请把你 认为正确的答案的字母代号填写在下表相应题号的方格内认为正确的答案的字母代号填写在下表相应题号的方格内. 1的相反数是（ ） A6 B C D6 2若 x3y4，则 1+3yx 的值是（ ） A3 B5 C3 D5 3若 m4，则估计 m 的值所在的范围是（ ） A1m2 B2m3 C3m4 D4m5 4某种病毒的最大直径为
2、 0.00000012 米，这一直径用科学记数法表示为（ ） A1.210 7 米 B1.210 8 米 C1.210 9 米 D1210 8 米 5直线 y2x 向下平移 2 个单位长度得到的直线是（ ） Ay2（x+2） By2（x2） Cy2x2 Dy2x+2 6如图所示的几何体的俯视图是（ ） A B C D 7箱子内装有 53 颗白球及 2 颗红球，小芬打算从箱子内抽球，以每次抽出一球后将球再放回的方式抽 53 次球若箱子内每颗球被抽到的机会相等，且前 52 次中抽到白球 51 次及红球 1 次，则第 53 次抽球时， 小芬抽到红球的几率为何？（ ） A B C D 8如图，BD 是
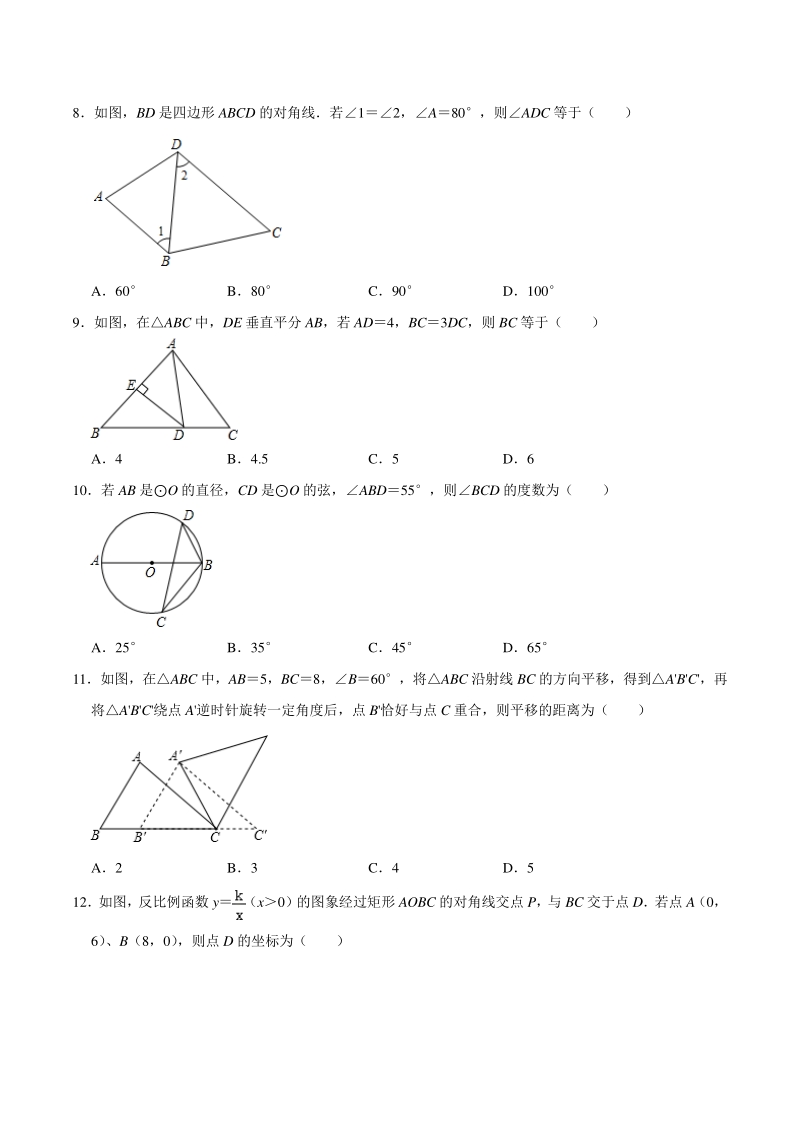
3、四边形 ABCD 的对角线若12，A80，则ADC 等于（ ） A60 B80 C90 D100 9如图，在ABC 中，DE 垂直平分 AB，若 AD4，BC3DC，则 BC 等于（ ） A4 B4.5 C5 D6 10若 AB 是O 的直径，CD 是O 的弦，ABD55，则BCD 的度数为（ ） A25 B35 C45 D65 11如图，在ABC 中，AB5，BC8，B60，将ABC 沿射线 BC 的方向平移，得到ABC，再 将ABC绕点 A逆时针旋转一定角度后，点 B恰好与点 C 重合，则平移的距离为（ ） A2 B3 C4 D5 12如图，反比例函数 y （x0）的图象经过矩形 AOBC
4、 的对角线交点 P，与 BC 交于点 D若点 A（0， 6） 、B（8，0） ，则点 D 的坐标为（ ） A （6，2） B （8，3） C D 二、填空题（本大题满分二、填空题（本大题满分 16 分，每小题分，每小题 4 分）分） 13 （4 分）分解因式：ab24ab+4a 14 （4 分）不等式组的解集为 15 （4 分） 如图， 在平行四边形 ABCD 中， 以点 A 为圆心， AD 长为半径作弧交 AB 于点 E；再分别以点 D、 E 为圆心，大于DE 长为半径作弧，两弧交于点 F；作射线 AF 交 DC 于点 G若 AB8，BC6，则 CG 的长为 16 （4 分）如图，在ABC
5、中，B90，AB6，BC4，点 O 在 AC 边上，O 与边 AB、BC 分别切 于点 D、E，则的值为 三、解答题（本大题满分三、解答题（本大题满分 0 分）分） 17 （1）计算： （1） 5+4（ ）2； （2）解方程：2 18疫情防控期间，某校为实现学生上下学“点对点”接送，计划组织本校全体走读生统一乘坐校园专线 上下学若单独调配 36 座新能源客车若干辆，则有 2 人没有座位；若单独调配 22 座新能源客车，则用 车数量将增加 4 辆，并空出 2 个座位 （1）计划调配 36 座新能源客车多少辆？该校共有多少名走读生？ （2）若同时调配 36 座和 22 座两种客车若干辆，既保证每人
6、有座，又保证每车不空座，则两种车型各需 多少辆？ 19海南省将从 2020 年 10 月 1 日起实施生活垃圾分类，某学校为此开展了主题为“垃圾分类，绿色生活 新时尚”的宣传活动为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部 分学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了如下不 完整的统计表和条形统计图 频数分布表 等级 频数 频率 优秀 42 0.42 良好 m 0.40 合格 12 n 待合格 6 0.06 请根据以上信息，解答下列问题： （1）本次调查随机抽取了 名学生； （2）在频数分布表中，m ，n ； （3）补全频数分
7、布直方图； （4）若全校有 2000 名学生，请估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有 人 20如图，要测量某山的高度 AB，小明先在山脚 C 点测得山顶 A 的仰角为 45，然后沿坡度为 1：的 斜坡走 100 米到达 D 点，在 D 点测得山顶 A 的仰角为 30，求这座山的高度 AB （结果保留整数） （参 考数据：1.41，1.73） 21如图 1 和图 2，在正方形 ABCD 中，点 E、F 在经过点 B 的直线 l 上，AEF 为等腰直角三角形，EAF 90，且点 F 始终在ABC 的内部，连接 DF （1） 当直线 l 绕点 B 旋转到如图 1 所示的位置时
8、， 求证： ABEADF； DFEF； EFBF+DF； （2）当直线 l 绕点 B 旋转到如图 2 所示的位置时，探究： （1）中的、三个结论是否仍然成立？ 若不成立，请直接写出正确的结论（不必证明） ； （3）在直线 l 绕点 B 旋转过程中，若正方形 ABCD 的边长为，DF1，求 AF 的长 22如图，已知抛物线与 x 轴交于 A（3，0） 、B（1，0）两点，与 y 轴交于点 C（0，3） ，对称轴 l 与 x 轴交于点 D，点 E 在 y 轴上，且 OEOBP 是该抛物线上的动点，连接 PA、PE，PD 与 AE 交于点 F （1）求该抛物线的函数表达式； （2）设点 P 的横坐标
9、为 t（310） 求PAE 的面积的最大值； 在对称轴 l 上找一点 M，使四边形 PAME 是平行四边形，求点 M 的坐标； 抛物线上存在点 P，使得PEF 是以 EF 为直角边的直角三角形，求点 P 的坐标，并判断此时PAE 的形状 2020 年海南省海口市中考数学模拟试卷（二）年海南省海口市中考数学模拟试卷（二） 参考答案与试题解析参考答案与试题解析 一、选择题（本大题满分一、选择题（本大题满分 36 分，每小题分，每小题 3 分）在下列各题的四个备选答案中，只有一个是正确的，请把你分）在下列各题的四个备选答案中，只有一个是正确的，请把你 认为正确的答案的字母代号填写在下表相应题号的方格
10、内认为正确的答案的字母代号填写在下表相应题号的方格内. 1的相反数是（ ） A6 B C D6 【分析】根据相反数的定义，即可解答 【解答】解：的相反数是，故选：C 2若 x3y4，则 1+3yx 的值是（ ） A3 B5 C3 D5 【分析】直接利用已知将原式变形得出答案 【解答】解：x3y4， 1+3yx1（x3y）143 故选：A 3若 m4，则估计 m 的值所在的范围是（ ） A1m2 B2m3 C3m4 D4m5 【分析】应先找到所求的无理数在哪两个和它接近的整数之间，然后判断出所求的无理数的范围即可求 解 【解答】解：364049， 67， 243 故选：B 4某种病毒的最大直径为
11、 0.00000012 米，这一直径用科学记数法表示为（ ） A1.210 7 米 B1.210 8 米 C1.210 9 米 D1210 8 米 【分析】绝对值小于 1 的正数也可以利用科学记数法表示，一般形式为 a10 n，与较大数的科学记数 法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的 0 的个数所决定 【解答】解：0.000 000121.210 7， 故选：A 5直线 y2x 向下平移 2 个单位长度得到的直线是（ ） Ay2（x+2） By2（x2） Cy2x2 Dy2x+2 【分析】据一次函数图象与几何变换得到直线 y2x 向下平移 2 个单位得到的函
12、数解析式为 y2x2 【解答】解：直线 y2x 向下平移 2 个单位得到的函数解析式为 y2x2 故选：C 6如图所示的几何体的俯视图是（ ） A B C D 【分析】根据俯视图的意义结合各个选项的图形进行判断即可 【解答】解：从上面看这个几何体，根据各个位置图形的形状，可知选项 C 中的图形符合题意， 故选：C 7箱子内装有 53 颗白球及 2 颗红球，小芬打算从箱子内抽球，以每次抽出一球后将球再放回的方式抽 53 次球若箱子内每颗球被抽到的机会相等，且前 52 次中抽到白球 51 次及红球 1 次，则第 53 次抽球时， 小芬抽到红球的几率为何？（ ） A B C D 【分析】让红球的个数
13、除以球的总数即为所求的概率 【解答】解：一个盒子内装有大小、形状相同的 53+255 个球，其中红球 2 个，白球 53 个， 小芬抽到红球的概率是： 故选：D 8如图，BD 是四边形 ABCD 的对角线若12，A80，则ADC 等于（ ） A60 B80 C90 D100 【分析】根据平行线的判定和性质定理即可得到结论 【解答】解：12， ABCD， A+ADC180， A80， ADC18080100， 故选：D 9如图，在ABC 中，DE 垂直平分 AB，若 AD4，BC3DC，则 BC 等于（ ） A4 B4.5 C5 D6 【分析】根据线段垂直平分线的性质即可得到结论 【解答】解：D
14、E 垂直平分 AB，若 AD4， BDAD4， BC3DC， BD2CD， CD2， BC6， 故选：D 10若 AB 是O 的直径，CD 是O 的弦，ABD55，则BCD 的度数为（ ） A25 B35 C45 D65 【分析】连接 AD，由 AB 是O 的直径得到ADB90，再根据互余计算出A 的度数，然后根据圆 周角定理即可得到C 的度数 【解答】解：连接 AD，如图， AB 是O 的直径， ADB90， ABD55， A905535， BCDA35 故选：B 11如图，在ABC 中，AB5，BC8，B60，将ABC 沿射线 BC 的方向平移，得到ABC，再 将ABC绕点 A逆时针旋转一
15、定角度后，点 B恰好与点 C 重合，则平移的距离为（ ） A2 B3 C4 D5 【分析】由旋转的性质和平移的性质可得 BCAC，ABAB5，BABC60，可证ABC 是等边三角形，可得 ABBC5，即可求解 【解答】解：将ABC绕点 A逆时针旋转一定角度后，点 B恰好与点 C 重合， BCAC， 将ABC 沿射线 BC 的方向平移，得到ABC， ABAB5，BABC60， ABC 是等边三角形， ABBC5， BB3， 平移的距离为 3， 故选：B 12如图，反比例函数 y （x0）的图象经过矩形 AOBC 的对角线交点 P，与 BC 交于点 D若点 A（0， 6） 、B（8，0） ，则点
16、D 的坐标为（ ） A （6，2） B （8，3） C D 【分析】根据矩形的性质可以找出点 P 的坐标，利用反比例函数图象上点的坐标特征即可求出反比例函 数解析式，再代入 x8 即可得出点 D 的坐标 【解答】解：四边形 AOBC 是矩形，且 A（0，6） 、B（8，0） ， P（4，3） 反比例函数 y的图象经过点 P， k4312， 反比例函数解析式为 y 把 x8 代入得，则 y， D（8，） ， 故选：C 二、填空题（本大题满分二、填空题（本大题满分 16 分，每小题分，每小题 4 分）分） 13 （4 分）分解因式：ab24ab+4a a（b2）2 【分析】先提取公因式 a，再根据
17、完全平方公式进行二次分解完全平方公式：a22ab+b2（ab） 2 【解答】解：ab24ab+4a a（b24b+4）（提取公因式） a（b2）2（完全平方公式） 故答案为：a（b2）2 14 （4 分）不等式组的解集为 x2 【分析】根据一元一次不等式组即可求出答案 【解答】解： 由得：x2 由得：x2 不等式组的解集为：x2 故答案为：x2 15 （4 分） 如图， 在平行四边形 ABCD 中， 以点 A 为圆心， AD 长为半径作弧交 AB 于点 E；再分别以点 D、 E 为圆心，大于DE 长为半径作弧，两弧交于点 F；作射线 AF 交 DC 于点 G若 AB8，BC6，则 CG 的长为
18、 2 【分析】依据平行四边形的性质以及角平分线的定义，即可得到 DG 和 DC 的长，再根据 CGCDDG 进行计算即可 【解答】解：四边形 ABCD 是平行四边形， CDAB8，ADBC6，ABCD， BAFDGA， AF 平分BAD， BAFDAF， DAFDGA， DGDA6， CGCDDG862， 故答案为：2 16 （4 分）如图，在ABC 中，B90，AB6，BC4，点 O 在 AC 边上，O 与边 AB、BC 分别切 于点 D、E，则的值为 【分析】 连接 OE、 OD， 易证四边形 OEBD 是正方形， 设 OEODDBBEr， 证明OECADO， 得出，求出 r，即可得出结果
19、 【解答】解：连接 OE、OD，如图所示： O 与 AB、BC 分别切于点 D、E， OECODA90，ODBBOEB90， ODOE， 四边形 OEBD 是正方形， OEODDBBE， 设 OEODDBBEr， 四边形 OEBD 是正方形， OEAB， COEA， OECODA， OECADO， ，即， 解得：r， ， 故答案为： 三、解答题（本大题满分三、解答题（本大题满分 0 分）分） 17 （1）计算： （1） 5+4（ ）2； （2）解方程：2 【分析】 （1）原式利用负整数指数幂法则，乘方的意义，以及二次根式乘法法则计算即可求出值； （2）分式方程去分母转化为整式方程，求出整式方程
20、的解得到 x 的值，经检验即可得到分式方程的解 【解答】解： （1）原式1+4 1+4 1+94 4； （2）去分母得：2x（x1）32（x21） ， 整理得：2x22x32x22， 解得：x， 经检验 x是分式方程的解 18疫情防控期间，某校为实现学生上下学“点对点”接送，计划组织本校全体走读生统一乘坐校园专线 上下学若单独调配 36 座新能源客车若干辆，则有 2 人没有座位；若单独调配 22 座新能源客车，则用 车数量将增加 4 辆，并空出 2 个座位 （1）计划调配 36 座新能源客车多少辆？该校共有多少名走读生？ （2）若同时调配 36 座和 22 座两种客车若干辆，既保证每人有座，又
21、保证每车不空座，则两种车型各需 多少辆？ 【分析】 （1）设计划调配 36 座新能源客车 x 辆，该学校共有 y 名走读学生，则需调配 22 座新能源客车 （x+4） 辆， 根据 “若单独调配 36 座新能源客车若干辆， 则有 2 人没有座位； 若只调配 22 座新能源客车， 则用车数量将增加 4 辆， 并空出 2 个座位” ， 即可得出关于 x， y 的二元一次方程组，解之即可得出结论； （2）设需调配 36 座客车 m 辆，22 座客车 n 辆，根据调配的车辆正好每人有座且每车不空座，即可得出 关于 m，n 的二元一次方程，结合 m，n 均为非负整数，即可得出结论 【解答】解： （1）设计
22、划调配 36 座新能源客车 x 辆，该校共有 y 名走读生 由题意，得， 解得， 答：计划调配 36 座新能源客车 6 辆，该校共有 218 名走读生 （2）设 36 座和 22 座两种车型各需 m，n 辆 由题意，得 36m+22n218，且 m，n 均为非负整数， 经检验，只有 m3，n5 符合题意 答：需调配 36 座客车 3 辆，22 座客车 5 辆 19海南省将从 2020 年 10 月 1 日起实施生活垃圾分类，某学校为此开展了主题为“垃圾分类，绿色生活 新时尚”的宣传活动为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部 分学生进行问卷调查，将他们的得分按优
23、秀、良好、合格、待合格四个等级进行统计，并绘制了如下不 完整的统计表和条形统计图 频数分布表 等级 频数 频率 优秀 42 0.42 良好 m 0.40 合格 12 n 待合格 6 0.06 请根据以上信息，解答下列问题： （1）本次调查随机抽取了 100 名学生； （2）在频数分布表中，m 40 ，n 0.12 ； （3）补全频数分布直方图； （4） 若全校有 2000 名学生， 请估计该校掌握垃圾分类知识达到 “优秀” 和 “良好” 等级的学生共有 1640 人 【分析】 （1）根据优秀等级频数及其频率可得答案； （2）根据频率频数总人数求解即可得出答案； （3）根据以上所求结果即可补全图
24、形； （4）用总人数乘以样本中优秀和良好等级的频率之和即可 【解答】解： （1）420.42100， 本次调查随机抽取了 100 名学生； 故答案为：100； （2）在频数分布表中，m1000.4040，n121000.12， 故答案为：40、0.12； （3）补全频数分布直方图如下： （4）估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有 2000（0.42+0.40）1640 （名） ， 故答案为：1640 20如图，要测量某山的高度 AB，小明先在山脚 C 点测得山顶 A 的仰角为 45，然后沿坡度为 1：的 斜坡走 100 米到达 D 点，在 D 点测得山顶 A 的仰角为
25、30，求这座山的高度 AB （结果保留整数） （参 考数据：1.41，1.73） 【分析】易证ABC 是等腰直角三角形，直角CDE 中已知边 CD 和DCE30，则三角形的三边的 长度可以得到 CE，DE 的长度，设 BCx，则 AF 和 DF 即可用含 x 的代数式表示出来，在直角ADF 中，利用三角函数即可得到一个关于 x 的方程，即可求得 x 的值 【解答】解：如图，过点 D 作 DEBC 于 E，作 DFAB 于 F，设 ABx 在 RtDEC 中， DCE30， ， AFABBFABDEx50 在 RtABC 中，ACB45， BCABx， 在 RtAFD 中，ADF30， ，即，
26、（米） 答：这座山的高度 AB 约为 237 米 21如图 1 和图 2，在正方形 ABCD 中，点 E、F 在经过点 B 的直线 l 上，AEF 为等腰直角三角形，EAF 90，且点 F 始终在ABC 的内部，连接 DF （1） 当直线 l 绕点 B 旋转到如图 1 所示的位置时， 求证： ABEADF； DFEF； EFBF+DF； （2）当直线 l 绕点 B 旋转到如图 2 所示的位置时，探究： （1）中的、三个结论是否仍然成立？ 若不成立，请直接写出正确的结论（不必证明） ； （3）在直线 l 绕点 B 旋转过程中，若正方形 ABCD 的边长为，DF1，求 AF 的长 【分析】 （1）
27、先判断出EABFAD，进而判断出ABEADF，进而得出AFDAEB45， EBDF，即可得出结论； （2）同（1）的方法，即可得出结论； （3）先求出 BD 和 BF，再分两种情况求出 EF，即可得出结论 【解答】解： （1）四边形 ABCD 是正方形， ABAD，BAD90 AEF 为等腰直角三角形，EAF90， AEAF，AEBAFE45， EAB+BAFFAD+BAF90， EABFAD， 在ABE 和ADF 中， ABEADF（SAS） ， ABEADF， AFDAEB45， DFBAFE+AFD90， DFEF ABEADF， EBDF， EFBF+EBBF+DF （2） （1）中的
28、、结论仍成立，结论不成立， 理由：四边形 ABCD 是正方形， ABAD，BAD90 AEF 为等腰直角三角形，EAF90， AEAF，AEBAFE45， EAB+BAFFAD+BAF90， EABFAD， 在ABE 和ADF 中， ABEADF（SAS） ， ABEADF， AFDAEB45， DFBAFE+AFD90， DFEF ABEADF， EBDF， EFBFEBBFDF； （3）在正方形 ABCD 中，AB， 在 RtBFD 中，DF1， 当 0CBF45时，由（1）知， 在 RtAEF 中， 当 45CBF90时，由（2）知， 在 RtAEF 中， 22如图，已知抛物线与 x 轴
29、交于 A（3，0） 、B（1，0）两点，与 y 轴交于点 C（0，3） ，对称轴 l 与 x 轴交于点 D，点 E 在 y 轴上，且 OEOBP 是该抛物线上的动点，连接 PA、PE，PD 与 AE 交于点 F （1）求该抛物线的函数表达式； （2）设点 P 的横坐标为 t（310） 求PAE 的面积的最大值； 在对称轴 l 上找一点 M，使四边形 PAME 是平行四边形，求点 M 的坐标； 抛物线上存在点 P，使得PEF 是以 EF 为直角边的直角三角形，求点 P 的坐标，并判断此时PAE 的形状 【分析】 （1）根据抛物线与 x 轴的两个交点坐标运用交点式，利用待定系数法求函数解析式； （
30、2）【解法一】过点 P 作 PHx 轴于点 H，交 AE 于点 I利用待定系数法求出直线 AE 的函数表达 式，根据题意用含 t 的代数式表示PAE 的面积，再运用求二次函数最值的方法即可； 【解法二】连接 PO，根据 SPAESPAO+SPEOSAOE将PAE 的面积表示成关于 t 的二次函数，再运 用求二次函数最值的方法即可； 利用平行四边形性质列方程求解即可； PEF 是以 EF 为直角边的直角三角形分两种情况：PEF90或PFE90，运用相似三角形 的判定和性质建立方程求解即可 【解答】解： （1）抛物线与 x 轴交于 A（3，0） 、B（1，0）两点， 设所求抛物线的函数表达式为 y
31、a（x+3） （x1） ， 把点 C（0，3）代入，得：3a（x+3） （x1） ， 解得：a1， 该抛物线的函数表达式为 y（x+3） （x1） ， 即：yx22x+3； （2）【解法一】如图 1，过点 P 作 PHx 轴于点 H，交 AE 于点 I， OEOB， E（0，1） ， 设直线 AE 的函数表达式为 ykx+b，将 A（3，0） ，E（0，1）分别代入， 得：， 解得：， 直线 AE 的表达式为， 由题意，点 P 的坐标为（t，t22t+3） ，则点 I 的坐标为， ， ，且3t0， 当时，PAE 的面积最大值为 【解法二】如图 1，连接 PO， 由题意，点 P 的坐标为（t，t
32、22t+3） ， SPAESPAO+SPEOSAOE AO|yP|+EO|xP|AOEO （t22t+3）+（t） t2t+3 （t+）2+， a0，且3t0， 当时，PAE 的面积最大值为 点 M 在抛物线 yx22x+3 的对称轴 x1 上， 设点 M 的坐标为（1，m） ， 由题意，点 P 的坐标为（t，t22t+3） ， 四边形 PAME 是平行四边形，AE、PM 为对角线， xP+xMxA+xE，即 t13+0， 解得：t2， 点 P 的坐标为（2，3） ， yP+yMyA+yE，得 3+m0+1， m2 点 M 的坐标为（1，2） PEF 是以 EF 为直角边的直角三角形分两种情况
33、： （）若PEF90，如图 2，过点 P 作 PGy 轴于点 G， PGEAOE90， PEG+AEO90，AEO+EAO90， PEGEAO， EPGAEO， ，即， 整理得 t2t20， 解得 t11，t22（舍去） ， 点 P 的坐标为（1，4） ， PGOE1， 1， PEAE， PAE 是等腰直角三角形 （）若PFE90，如图 3，过点 P 作 PHx 轴于点 H， PHDAOE90， DPH+PDH90， AFDPFE90， PDH+EAO90， DPHEAO， PHDAOE， ，即， 整理得 t2t60， 解得 t12，t23（舍去） ， 点 P 的坐标为（2，3） ， H（2，0） ， PH3，AHOAOH321， PHOA，AHOE，PHAAOE90， PHAAOE（SAS） ， PAE 是等腰三角形 综上所述，P 的坐标为（1，4） ，PAE 是等腰直角三角形；或 P 的坐标为（2，3） ，PAE 是等腰 三角形
