 2021年重庆市沙坪坝区三校联考中考数学诊断试卷(3月份)含答案解析
2021年重庆市沙坪坝区三校联考中考数学诊断试卷(3月份)含答案解析
《2021年重庆市沙坪坝区三校联考中考数学诊断试卷(3月份)含答案解析》由会员分享,可在线阅读,更多相关《2021年重庆市沙坪坝区三校联考中考数学诊断试卷(3月份)含答案解析(37页珍藏版)》请在七七文库上搜索。
1、2021 年重庆市沙坪坝区三校联考中考数学诊断试卷年重庆市沙坪坝区三校联考中考数学诊断试卷(3 月份)月份) 一、选择题: (本大题一、选择题: (本大题 12 个小题,每小题个小题,每小题 4 分,共分,共 48 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。 1 (4 分)在下列“禁毒” 、 “和平” 、 “志愿者” 、 “节水”这四个标志中,属于轴对称图形的是( ) A B C D 2
2、 (4 分)重庆是全国重点旅游城市,2020 年实现旅游总收入约为 57 400 000 万元,数据 57 400 000 用科 学记数法可表示 为( ) A0.574108 B5.74108 C5.74107 D574105 3 (4 分)如图,已知ABC 与DEF 位似,位似中心为点 O,且 AB:DE3:2,则ABC 的面积与 DEF 面积之比为( ) A3:2 B3:5 C9:4 D9:5 4 (4 分)函数中,x 的取值范围是( ) Ax5 Bx5 且 x0 Cx5 且 x0 Dx5 5 (4 分)若 x1 是关于 x 的一元二次方程 ax2+bx10 的一个根,则 20212a+2
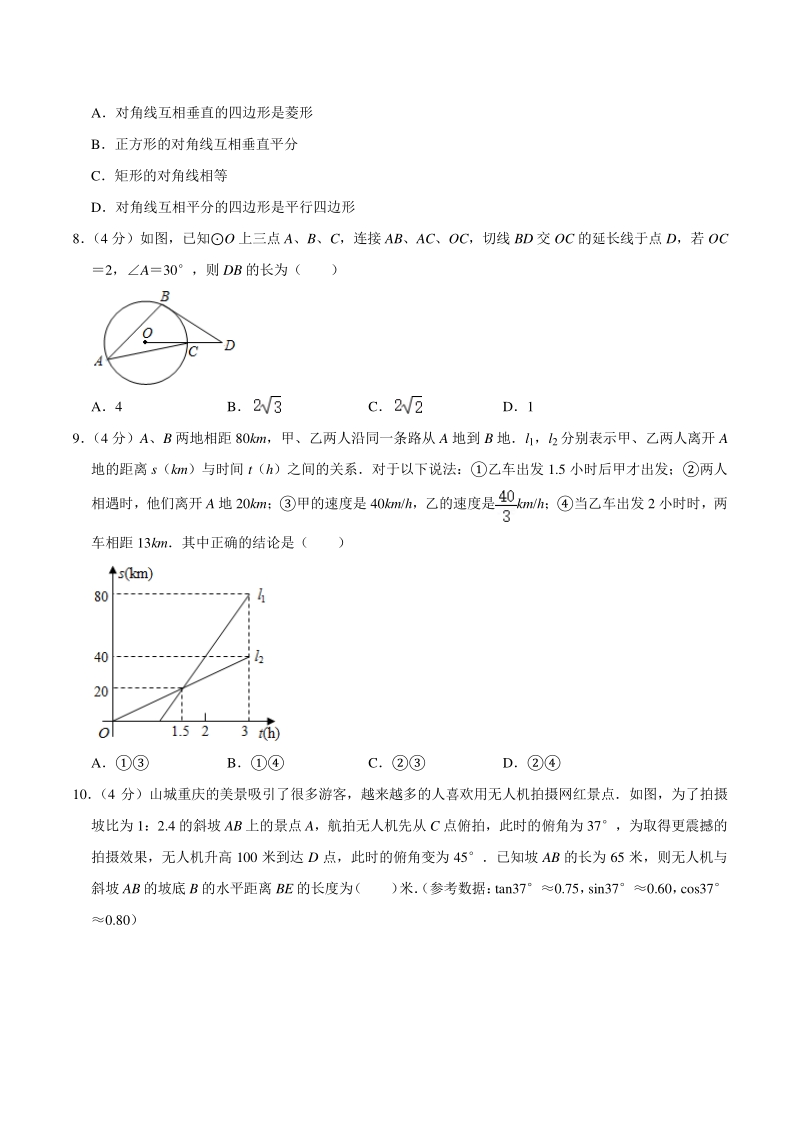
3、b 的值为( ) A2019 B2020 C2022 D2023 6 (4 分)已知一次函数 ykx+2 的图象经过点 A,且 y 随 x 的增大而减小,则点 A 的坐标可以是( ) A (1,2) B (2,1) C (2,3) D (3,4) 7 (4 分)下列命题中,假命题是( ) A对角线互相垂直的四边形是菱形 B正方形的对角线互相垂直平分 C矩形的对角线相等 D对角线互相平分的四边形是平行四边形 8 (4 分)如图,已知O 上三点 A、B、C,连接 AB、AC、OC,切线 BD 交 OC 的延长线于点 D,若 OC 2,A30,则 DB 的长为( ) A4 B C D1 9 (4 分
4、)A、B 两地相距 80km,甲、乙两人沿同一条路从 A 地到 B 地l1,l2分别表示甲、乙两人离开 A 地的距离 s(km)与时间 t(h)之间的关系对于以下说法:乙车出发 1.5 小时后甲才出发;两人 相遇时,他们离开 A 地 20km;甲的速度是 40km/h,乙的速度是km/h;当乙车出发 2 小时时,两 车相距 13km其中正确的结论是( ) A B C D 10 (4 分)山城重庆的美景吸引了很多游客,越来越多的人喜欢用无人机拍摄网红景点如图,为了拍摄 坡比为 1:2.4 的斜坡 AB 上的景点 A,航拍无人机先从 C 点俯拍,此时的俯角为 37,为取得更震撼的 拍摄效果,无人机
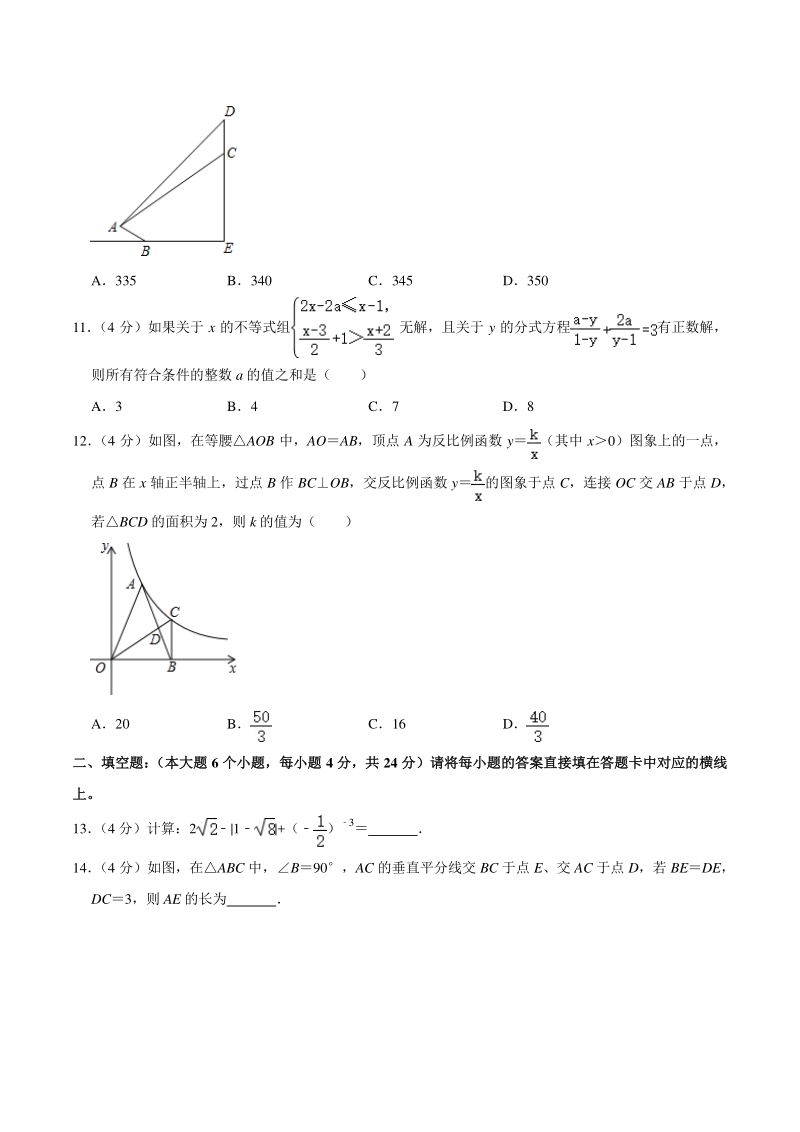
5、升高 100 米到达 D 点,此时的俯角变为 45已知坡 AB 的长为 65 米,则无人机与 斜坡 AB 的坡底 B 的水平距离 BE 的长度为 ( ) 米(参考数据: tan370.75, sin370.60, cos37 0.80) A335 B340 C345 D350 11 (4 分)如果关于 x 的不等式组无解,且关于 y 的分式方程有正数解, 则所有符合条件的整数 a 的值之和是( ) A3 B4 C7 D8 12 (4 分)如图,在等腰AOB 中,AOAB,顶点 A 为反比例函数 y(其中 x0)图象上的一点, 点 B 在 x 轴正半轴上,过点 B 作 BCOB,交反比例函数 y
6、的图象于点 C,连接 OC 交 AB 于点 D, 若BCD 的面积为 2,则 k 的值为( ) A20 B C16 D 二、填空题: (本大题二、填空题: (本大题 6 个小题,每小题个小题,每小题 4 分,共分,共 24 分)请将每小题的答案直接填在答题卡中对应的横线分)请将每小题的答案直接填在答题卡中对应的横线 上。上。 13 (4 分)计算:2|1|+() 3 14 (4 分)如图,在ABC 中,B90,AC 的垂直平分线交 BC 于点 E、交 AC 于点 D,若 BEDE, DC3,则 AE 的长为 15 (4 分)现从2,3 中,任取两个不同的数分别作为二次函数 yax22x+b 中
7、的 a 和 b,则 所得抛物线与 x 轴有公共点的概率为 16 (4 分)如图,在矩形 ABCD 中,AB3,AD2,以 A 为圆心,AD 为半径作圆交 AB 于点 E,F 为的 中点,过 F 作 CD 的平行线,交 AD 于点 G,交 BC 于点 H,则阴影部分的面积为 17 (4 分)如图,在ABC 中,点 D 是线段 AB 上的一点,过点 D 作 DEAC 交 BC 于点 E,将BDE 沿 DE 翻折,得到BDE,若点 C 恰好在线段 BD 上,若BCD90,DC:CB3:2,AB16则 CE 的长度为 18 (4 分)元旦节前,某商店购进了一批 A、B 款式的大灯笼和若干小灯笼,其中小
8、灯笼个数占灯笼总个 数的 80%,它们的进价之比为 10:20:1,店主将三种灯笼分别加价 50%、40%、100%进行销售,全部 售完后利润率为 54%年关将至,该商店又购进了这三种灯笼,且进货量和之前分别相同,但是 A、B 款式的大灯笼进价分别上涨了 50%、25%,小灯笼进价不变,于是店主将这两种大灯笼的价格分别在现 在的进价基础上加价 60%、40%进行销售,且购买一个 A 款式的大灯笼赠送两个小灯笼,购买一个 B 款 式的大灯笼赠送 4 个小灯笼,余下的小灯笼售价与之前相同,那么这批灯笼卖完后,利润率为 三、解答题(本大题共三、解答题(本大题共 6 个小题,每题个小题,每题 10 分
9、,共分,共 60 分) ,解答时每小题都必须写分) ,解答时每小题都必须写出必要的演算过程或推理出必要的演算过程或推理 步骤,请将解答过程书写在答题卡中对应的位置上。步骤,请将解答过程书写在答题卡中对应的位置上。 19 (10 分)计算: (1) (x2y)2x(x4y) ; (2)+1 20 (10 分)目前,重庆市正全面开展生活垃圾分类工作随着生活垃圾分类的全面推广,一些街镇也积极 行动起来,通过入户宣传、开展各种趣味活动等,提高居民参与生活垃圾分类的积极性为了进一步提 高垃圾分类的准确度,某社区对甲、乙两个小区的居民进行了有关垃圾分类常识的测试,并从甲、乙两 小区各随机抽取 20 名居民
10、的测试成绩进行整理分析(成绩得分用 x 表示,共分成四组:A10 x15, B15x20,C20 x25,D25x30) ,下面给出了部分信息: 甲小区 20 名居民测试成绩:13,15,16,19,20,21,22,23,24,25,25,26,27,27,28,28,28, 29,30,30 乙小区 20 名居民测试成绩在 C 组中的数据是:20,23,21,24,22,21 甲、乙两小区被抽取居民的测试成绩统计表 平均数 中位数 方差 甲小区 23.8 25 25.75 乙小区 22.3 b 24.34 根据以上信息,解答下列问题: (1)a ,b ; 根据以上数据,你认为 小区(填“甲
11、”或“乙” )垃圾分类的准确度更高,说明理由: ; (2)若甲、乙两个校区居民共 2400 人,估计两个小区测试成绩优秀(x25)的居民人数是多少? 21 (10 分)已知:在ABC 中,ABAC,BDAC 交 AC 于 D (1)尺规作图:作线段 BC 的垂直平分线交 BD 于 O,交 BC 于 E,连接 CO; (2)若BAC56,求DOC 的度数 22 (10 分)学习函数时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质 的过程结合已有的学习经验,下面我们对函数的图象和性质进行探究,请将 以下探究过程补充完整: (1)选取适当的值补全表格;描点、连线,在所给的平
12、面直角坐标系中画出函数的图象: x y (2)结合图象,写出该函数的一条性质: ; (3)结合这个函数的图象与性质,解决下列问题: 若点 A(x1,y1) ,B(x2,y2) ,C(x3,y3)在这个函数的图象上,且 0 x33,1x1x20,请 写出 y1,y2,y3的大小关系: (用“”连接) 若直线 y2a+1(a 是常数)与该函数图象有且只有三个交点,则 a 的取值范围为 23 (10 分)在大力推广垃圾分类之前,某小区虽然在每栋楼都放置了可回收垃圾桶和不可回收垃圾桶,但 是少数居民对垃圾分类的认识不够深入,常常将垃圾混装后随意丢入垃圾桶,导致垃圾分类混乱,垃圾 处理站将可回收垃圾桶内
13、的垃圾记为 A 类垃圾,将不可回收垃圾桶内的垃圾记为 B 类垃圾该小区共有 10 栋楼,平均每栋楼每月产生 12 吨 A 类垃圾和 4 吨 B 类垃圾,每吨 B 类垃圾处理费是每吨 A 类垃圾处 理费的 2 倍,该小区每月 A、B 两类垃圾处理费总费用为 8000 元 (1)求每吨 A 类垃圾处理费多少元? (2)在大力推广垃圾分类之后,该小区的居民认识到了垃圾分类的重要性并规范地放置垃圾该小区每 月产生的 A、B 两类垃圾总重量不变的情况下,B 类垃圾的重量增加了 a%,同时,垃圾处理站通过技术 革新将 A、B 两类垃圾每吨处理费分别降低了a%和a%,这样与推广垃圾分类之前相比,该小区每 月
14、 A、B 两类垃圾处理费总费用减少了a%,求 a 的值 24 (10 分)如果一个三位数满足各位数字都不为 0,且个位数字比十位数字大 1,则称这个三位数为完美 数若 m、n 都是完美数,将组成 m 的各数位上的数字中最大数字作为两位数 p 的十位上的数字,组成 n 的各数位上的数字中最大数字作为两位数 p 的个位上的数字,再将组成 m 的各数位上的数字中最小数 字作为两位数 q 的十位上的数字,组成 n 的各数位上的数字中最小数字作为两位数 q 的个位上的数字, 所得的这两个数 p、q 之和记为 F(m,n) 例如:因为 1+12,4+15,所以 112 和 645 都是完美数,则 F(11
15、2,645)26+1440 因为 1+12,8+19,所以 212 和 689 都是完美数,则 F(212,689)29+1645 (1)判断 623 和 456 是否为完美数并说明原因如果都是完美数则计算 F(623,456)的值 (2)若 s、t 都是完美数,其中 s400+10 x+y,t310+100a+b(1x8,1y9,0a5,1b9 且 x、y、a、b 都是整数) ,规定:K(s,t)|st|,当 F(s,123)F(t,867)20 时,求 K(s,t) 的最小值 四、解答题: (本大题共四、解答题: (本大题共 2 个小题,其中个小题,其中 25 题题 10 分,分,26 题
16、题 8 分,共分,共 18 分) 。解答时每小题都必须写出必分) 。解答时每小题都必须写出必 要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。要的演算过程或推理步骤,请将解答过程书写在答题卡中对应的位置上。 25 (10 分)在平面直角坐标系中,抛物线 yax2+bx+c(a0)与 x 轴交于 A,B 两点(A 在 B 的左侧) , 与 y 轴交于点 C(0,6) ,其中 AB8,tanCAB3 (1)求抛物线的表达式; (2) 点 P 是直线 BC 上方抛物线上一点, 过点 P 作 PDAC 交 x 轴于点 D, 交 BC 于点 E, 求 BE 的最大值及点 P 的坐标 (3
17、)将该抛物线沿射线 CA 方向平移 2个单位长度得到抛物线 y1,平移后的抛物线与原抛物线相交 于点 F, 点 G 为抛物线 y1的顶点, 点 M 为直线 FG 上一点, 点 N 为平面上一点 在 (2) 中, 当 BE 的值最大时,是否存在以 P、E、M、N 为顶点的四边形是菱形,若存在,直接写出点 N 的坐标;若 不存在,请说明理由 26 (8 分)如图,已知ABC 中,ABC45,CD 是边 AB 上的高线,E 是 AC 上一点,连接 BE,交 CD 于点 F (1)如图 1,若ABE15,BC+1,求 DF 的长; (2)如图 2,若 BFAC,过点 D 作 DGBE 于点 G,求证:
18、BECE+2DG; (3)如图 3,若 R 为射线 BA 上的一个动点,以 BR 为斜边向外作等腰直角BRH,M 为 RH 的中点在 (2)的条件下,将CEF 绕点 C 旋转,得到CEF,E,F 的对应点分别为 E,F,直线 MF与直线 AB 交于点 P,tanACD,直接写出当 MF取最小值时的值 参考答案与试题解析参考答案与试题解析 一、选择题: (本大题一、选择题: (本大题 12 个小题,每小题个小题,每小题 4 分,共分,共 48 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案
19、所对应的方框涂黑。的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑。 1 (4 分)在下列“禁毒” 、 “和平” 、 “志愿者” 、 “节水”这四个标志中,属于轴对称图形的是( ) A B C D 【分析】根据轴对称图形的概念进行判断即可 【解答】解:A、不是轴对称图形,故选项错误; B、是轴对称图形,故选项正确; C、不是轴对称图形,故选项错误; D、不是轴对称图形,故选项错误 故选:B 2 (4 分)重庆是全国重点旅游城市,2020 年实现旅游总收入约为 57 400 000 万元,数据 57 400 000 用科 学记数法可表示 为( ) A0.574108
20、 B5.74108 C5.74107 D574105 【分析】科学记数法的表示形式为 a10n的形式,其中 1|a|10,n 为整数确定 n 的值时,要看把 原数变成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同当原数绝对值10 时,n 是正整数;当原数的绝对值1 时,n 是负整数 【解答】解:574000005.74107 故选:C 3 (4 分)如图,已知ABC 与DEF 位似,位似中心为点 O,且 AB:DE3:2,则ABC 的面积与 DEF 面积之比为( ) A3:2 B3:5 C9:4 D9:5 【分析】利用位似的性质得到ABCDEF,然后根据相似三角形的性质求解
21、【解答】解:ABC 与DEF 位似,位似中心为点 O, ABCDEF, ABC 的面积与DEF 面积之比()2()2 故选:C 4 (4 分)函数中,x 的取值范围是( ) Ax5 Bx5 且 x0 Cx5 且 x0 Dx5 【分析】根据被开方数大于等于 0,列式计算即可得解 【解答】解:由题意得,x+50, 解得 x5, 故选:D 5 (4 分)若 x1 是关于 x 的一元二次方程 ax2+bx10 的一个根,则 20212a+2b 的值为( ) A2019 B2020 C2022 D2023 【分析】将 x1 代入方程得出 ab1,再整体代入计算可得 【解答】解:将 x1 代入方程,得:a
22、b10, 则 ab1, 所以原式20212(ab) 202121 20212 2019, 故选:A 6 (4 分)已知一次函数 ykx+2 的图象经过点 A,且 y 随 x 的增大而减小,则点 A 的坐标可以是( ) A (1,2) B (2,1) C (2,3) D (3,4) 【分析】由 y 随 x 的增大而减小,利用一次函数的性质可得出 k0,由各选项中点的坐标,利用一次函 数图象上点的坐标特征可得出关于 k 的一元一次方程,解之即可得出 k 的值,取 k 值为负的选项即可得 出结论 【解答】解:y 随 x 的增大而减小, k0 A、当点(1,2)在一次函数 ykx+2 的图象上时,k+
23、22, 解得:k0,选项 A 不符合题意; B、当点(2,1)在一次函数 ykx+2 的图象上时,2k+21, 解得:k,选项 B 符合题意; C、当点(2,3)在一次函数 ykx+2 的图象上时,2k+23, 解得:k,选项 C 不符合题意; D、当点(3,4)在一次函数 ykx+2 的图象上时,3k+24, 解得:k,选项 D 不符合题意 故选:B 7 (4 分)下列命题中,假命题是( ) A对角线互相垂直的四边形是菱形 B正方形的对角线互相垂直平分 C矩形的对角线相等 D对角线互相平分的四边形是平行四边形 【分析】对各个命题逐一判断后找到错误的即可确定假命题 【解答】解:A、对角线互相垂
24、直的平行四边形是菱形,原命题是假命题; B、正方形的对角线互相垂直平分,是真命题; C、矩形的对角线相等,是真命题; D、对角线互相平分的四边形是平行四边形,是真命题; 故选:A 8 (4 分)如图,已知O 上三点 A、B、C,连接 AB、AC、OC,切线 BD 交 OC 的延长线于点 D,若 OC 2,A30,则 DB 的长为( ) A4 B C D1 【分析】连接 OB,如图,根据切线的性质得OBD90,再根据圆周角定理得到BOC60,然 后根据含 30 度的直角三角形三边的关系求 BD 的长 【解答】解:连接 OB,如图, BD 为切线, OBBD, OBD90, BOC2A23060,

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2021 重庆市 沙坪坝区 联考 中考 数学 诊断 试卷 月份 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-179543.html