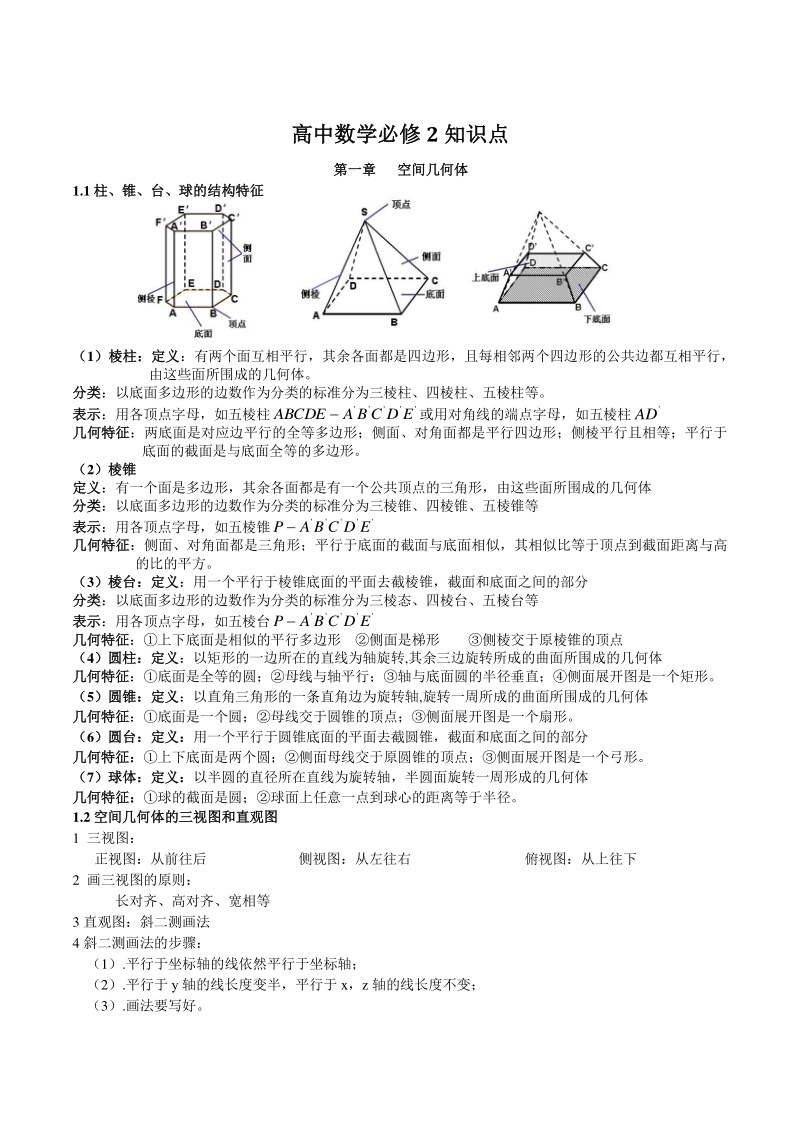
1、 高中数学必修高中数学必修 2 知识点知识点 第一章第一章 空间几何体空间几何体 1.1 柱、锥、台、球的结构特征柱、锥、台、球的结构特征 （1）棱柱：定义）棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行， 由这些面所围成的几何体。 分类分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。 表示表示：用各顶点字母，如五棱柱 EDCBAABCDE 或用对角线的端点字母，如五棱柱 AD 几何特征几何特征：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于 底面的截面是与底面全等的多边形。 （2）棱锥）棱锥 定义
2、定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体 分类分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等 表示表示：用各顶点字母，如五棱锥 EDCBAP 几何特征几何特征：侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高 的比的平方。 （3）棱台：定义）棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分 分类分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等 表示表示：用各顶点字母，如五棱台 EDCBAP 几何特征几何特征：上下底面是相似的平行多边形 侧面是梯形 侧棱交于原棱锥
3、的顶点 （4）圆柱：定义）圆柱：定义：以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体 几何特征几何特征：底面是全等的圆；母线与轴平行；轴与底面圆的半径垂直；侧面展开图是一个矩形。 （5）圆锥：定义）圆锥：定义：以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征几何特征：底面是一个圆；母线交于圆锥的顶点；侧面展开图是一个扇形。 （6）圆台：定义：）圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分 几何特征：几何特征：上下底面是两个圆；侧面母线交于原圆锥的顶点；侧面展开图是一个弓形。 （7）球体：定义：）球体：定义：以半圆的直径所
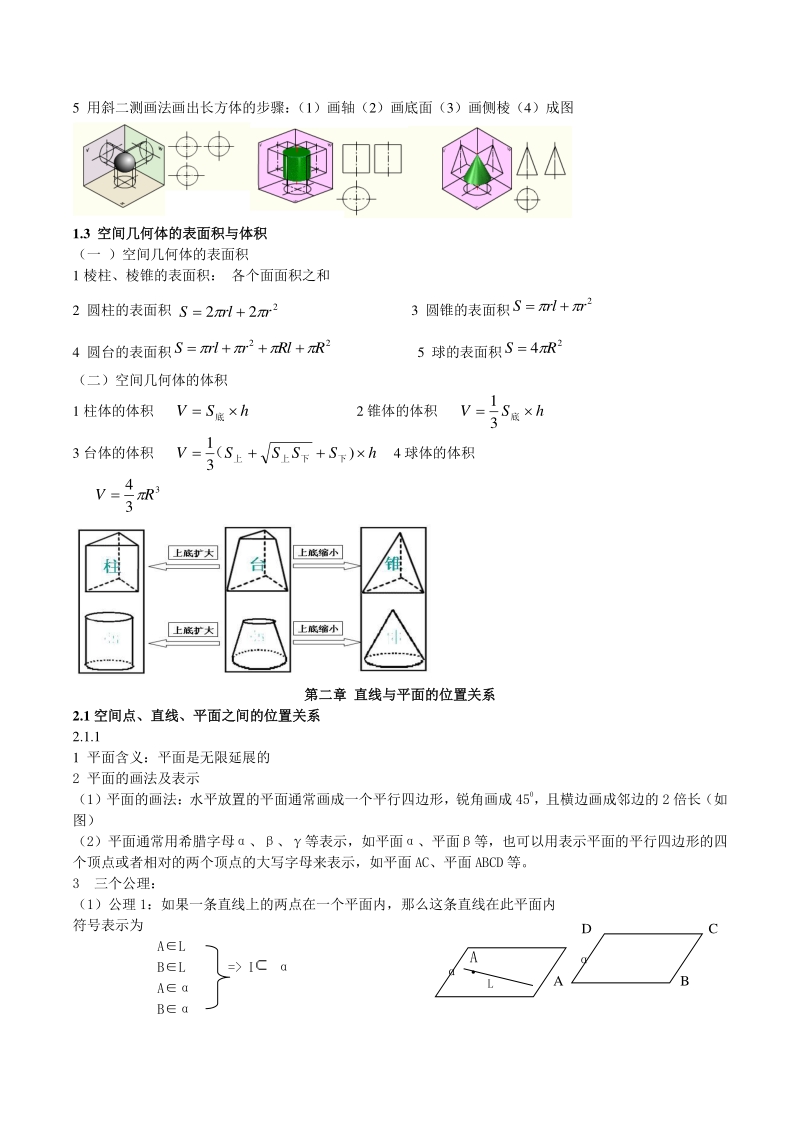
4、在直线为旋转轴，半圆面旋转一周形成的几何体 几何特征：几何特征：球的截面是圆；球面上任意一点到球心的距离等于半径。 1.2 空间几何体的三视图和直观图空间几何体的三视图和直观图 1 三视图： 正视图：从前往后 侧视图：从左往右 俯视图：从上往下 2 画三视图的原则： 长对齐、高对齐、宽相等 3 直观图：斜二测画法 4 斜二测画法的步骤： （1）.平行于坐标轴的线依然平行于坐标轴； （2）.平行于 y 轴的线长度变半，平行于 x，z 轴的线长度不变； （3）.画法要写好。 D C B A 5 用斜二测画法画出长方体的步骤： （1）画轴（2）画底面（3）画侧棱（4）成图 1.3 空间几何体的表面积
5、与体积空间几何体的表面积与体积 （一 ）空间几何体的表面积 1 棱柱、棱锥的表面积： 各个面面积之和 2 圆柱的表面积 3 圆锥的表面积 2 rrlS 4 圆台的表面积 22 RRlrrlS 5 球的表面积 2 4 RS （二）空间几何体的体积 1 柱体的体积 hSV 底 2 锥体的体积 hSV 底 3 1 3 台体的体积 hSSSSV) 3 1 下下上上 （ 4 球体的体积 3 3 4 RV 第二章第二章 直线与平面的位置关系直线与平面的位置关系 2.1 空间点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系 2.1.1 1 平面含义：平面是无限延展的 2 平面的画法及表示 （1）
6、平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成 45 0，且横边画成邻边的 2 倍长（如 图） （2）平面通常用希腊字母、等表示，如平面、平面等，也可以用表示平面的平行四边形的四 个顶点或者相对的两个顶点的大写字母来表示，如平面 AC、平面 ABCD 等。 3 三个公理： （1）公理 1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内 符号表示为 AL BL = L A B 2 22rrlS L A P L 公理 1 作用：判断直线是否在平面内 （2）公理 2：过不在一条直线上的三点，有且只有一个平面。 符号表示为：A、B、C 三点不共线 = 有且只有一个平面， 使 A、
7、B、C。 公理 2 作用：确定一个平面的依据。 （3）公理 3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。 符号表示为：P =L，且 PL 公理 3 作用：判定两个平面是否相交的依据 2.1.2 空间中直线与直线之间的位置关系空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系： 相交直线：同一平面内，有且只有一个公共点； 平行直线：同一平面内，没有公共点； 异面直线： 不同在任何一个平面内，没有公共点。 2 公理 4：平行于同一条直线的两条直线互相平行。 符号表示为：设 a、b、c 是三条直线 ab cb 强调：公理 4 实质上是说平行具有传递性，在
8、平面、空间这个性质都适用。 公理 4 作用：判断空间两条直线平行的依据。 3 等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补 4 注意点： a与 b所成的角的大小只由 a、b 的相互位置来确定，与O的选择无关，为简便，点O一般取在两直 线中的一条上； 两条异面直线所成的角(0， )； 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作 ab； 两条直线互相垂直，有共面垂直与异面垂直两种情形； 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。 2.1.3 2.1.4 空间中直线与平面、平面与平面之间的位置关系空间中直线与平面、平面与平面之间的
9、位置关系 1、直线与平面有三种位置关系： （1）直线在平面内 有无数个公共点 （2）直线与平面相交 有且只有一个公共点 （3）直线在平面平行 没有公共点 指出：直线与平面相交或平行的情况统称为直线在平面外，可用 a 来表示 a a=A a 2.2.2.直线、平面平行的判定及其性质直线、平面平行的判定及其性质 2.2.1 直线与平面平行的判定直线与平面平行的判定 1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。 简记为：线线平行，则线面平行。 C B A 共面直线 =ac 2 符号表示： a b = a ab 2.2.2 平面与平面平行的判定平面与平面
10、平行的判定 1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。 符号表示： a b ab = P a b 2、判断两平面平行的方法有三种： （1）用定义； （2）判定定理； （3）垂直于同一条直线的两个平面平行。 2.2.3 2.2.4 直线与平面、平面与平面平行的性质直线与平面、平面与平面平行的性质 1、定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。 简记为：线面平行则线线平行。 符号表示： a a ab = b 作用：利用该定理可解决直线间的平行问题。 2、定理：如果两个平面同时与第三个平面相交，那么它们的交线平行。 符
11、号表示： = a ab = b 作用：可以由平面与平面平行得出直线与直线平行 2.3 直线、平面垂直的判定及其性质 2.3.1 直线与平面垂直的判定直线与平面垂直的判定 1、定义 如果直线 L 与平面内的任意一条直线都垂直，我们就说直线 L 与平面互相垂直，记作 L，直线 L 叫做平面的垂线，平面叫做直线 L 的垂面。如图，直线与平面垂直时,它们唯一公共点 P 叫做垂足。 L p 2、判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。 注意点： a)定理中的“两条相交直线”这一条件不可忽视； b)定理体现了
12、“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想。 2.3.2 平面与平面垂直的判定平面与平面垂直的判定 1、二面角的概念：表示从空间一直线出发的两个半平面所组成的图形 A 梭 l B 2、二面角的记法：二面角-l-或-AB- 3、两个平面互相垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。一个平面过另一个平面的垂线，则这两个平面垂直。 2.3.3 2.3.4 直线与平面直线与平面、平面与平面垂直平面与平面垂直的性质的性质 1、定理：垂直于同一个平面的两条直线平行。 2 性质定理： 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。 本章知识结构框图本章知识结构
13、框图 第三章第三章 直线与方程直线与方程 3.1 直线的倾斜角和斜率直线的倾斜角和斜率 3.1 倾斜角和斜率倾斜角和斜率 1、直线的倾斜角的概念：当直线 l 与 x 轴相交时, 取 x 轴作为基准, x 轴正向与直线 l 向上方向之间所成 的角叫做直线 l 的倾斜角.特别地,当直线 l 与 x 轴平行或重合时, 规定= 0. 2、 倾斜角的取值范围： 0180. 当直线 l 与 x 轴垂直时, = 90. 3、直线的斜率: 一条直线的倾斜角(90)的正切值叫做这条直线的斜率,斜率常用小写字母 k 表示,也就是 k = tan 当直线 l 与 x 轴平行或重合时, =0, k = tan0=0;
14、 平面（公理 1、公理 2、公理 3、公理 4） 空间直线、平面的位置关系 平面与平面的位置关系 直线与平面的位置关系 直线与直线的位置关系 22 1 22221 PPxxyy 当直线 l 与 x 轴垂直时, = 90, k 不存在. 由此可知, 一条直线 l 的倾斜角一定存在,但是斜率 k 不一定存在. 4、 直线的斜率公式: 给定两点 P1(x1,y1),P2(x2,y2),x1x2,用两点的坐标来表示直线 P1P2 的斜率： 斜率公式斜率公式: k=y2: k=y2- -y1/x2y1/x2- -x1 x1 3.1.2 两条直线的平行与垂直两条直线的平行与垂直 1、两条直线都有斜率而且不
15、重合，如果它们平行，那么它们的斜率相等；反之，如果它们的斜率相等，那 么它们平行， 即 注意: 上面的等价是在两条直线不重合且斜率存在的前提下才成立的，缺少这个前提，结论并不成立即 如果 k1=k2, 那么一定有 L1L2 2、两条直线都有斜率，如果它们互相垂直，那么它们的斜率互为负倒数；反之，如果它们的斜率互为负倒 数，那么它们互相垂直，即 3.2.1 直线的点斜式方程直线的点斜式方程 1、直线的点斜式点斜式方程：直线l经过点),( 000 yxP，且斜率为k )( 00 xxkyy 2、直线的斜截式斜截式方程：已知直线l的斜率为k，且与y轴的交点为), 0(b bkxy 3.2.2 直线的
16、两点式方程直线的两点式方程 1、直线的两点式方程：已知两点),(),( 222211 yxPxxP其中),( 2121 yyxx y-y1/y-y2=x-x1/x-x2 2、 直线的截距式方程： 已知直线l与x轴的交点为 A)0 ,(a， 与y轴的交点为 B), 0(b， 其中0, 0ba 3.2.3 直线的一般式方程直线的一般式方程 1、直线的一般式方程：关于yx,的二元一次方程0CByAx（A，B 不同时为 0） 2、各种直线方程之间的互化。 3.3 直线的交点坐标与距离公式直线的交点坐标与距离公式 3.3.1 两直线的交点坐标两直线的交点坐标 1、给出例题：两直线交点坐标 L1 ：3x+
17、4y-2=0 L1：2x+y +2=0 3420 2220 xy xy 解 ： 解 方 程 组 得 x=-2，y=2 所以 L1 与 L2 的交点坐标为 M（-2，2） 3.3.2 两点间距离两点间距离 两点间的距离公式 3.3.3 点到直线的距离公式点到直线的距离公式 1点到直线距离公式： 点),( 00 yxP到直线0:CByAxl的距离为： 22 00 BA CByAx d 2 2、两平行线间的距离公式： 已知两条平行线直线 1 l和 2 l的一般式方程为 1 l：0 1 CByAx， 2 l0 2 CByAx，则 1 l与 2 l的距离为 22 21 BA CC d 第四章第四章 圆与
18、方程圆与方程 4.1.1 圆的标准方程圆的标准方程 1、圆的标准方程： 222 ()()xaybr 圆心为 A(a,b),半径为 r 的圆的方程 2、点 00 (,)M xy与圆 222 ()()xaybr的关系的判断方法： （1） 22 00 ()()xayb 2 r，点在圆外 （2） 22 00 ()()xayb= 2 r，点在圆上 （3） 22 00 ()()xayb 2 r，点在圆内 4.1.2 圆的一般方程圆的一般方程 1、圆的一般方程：0 22 FEyDxyx 2、圆的一般方程的特点： (1)x2 和 y2 的系数相同，不等于 0 没有 xy 这样的二次项 (2)圆的一般方程中有三
19、个特定的系数 D、E、F，因之只要求出这三个系数，圆的方程就确定了 (3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指 出了圆心坐标与半径大小，几何特征较明显。 4.2.1 圆与圆的位置关系圆与圆的位置关系 1、用点到直线的距离来判断直线与圆的位置关系 设直线l：0cbyax，圆C：0 22 FEyDxyx，圆的半径为r，圆心) 2 , 2 ( ED 到直线 的距离为d，则判别直线与圆的位置关系的依据有以下几点： （1）当rd 时，直线l与圆C相离； （2）当rd 时，直线l与圆C相切； （3）当rd 时，直线l与圆C相交； 4.2.2 圆与圆的位置关系圆
20、与圆的位置关系 两圆的位置关系 设两圆的连心线长为l，则判别圆与圆的位置关系的依据有以下几点： （1）当 21 rrl时，圆 1 C与圆 2 C相离； （2）当 21 rrl时，圆 1 C与圆 2 C外切； （3）当| 21 rr 21 rrl时，圆 1 C与圆 2 C相交； （4）当| 21 rrl时，圆 1 C与圆 2 C内切； （5）当| 21 rrl时，圆 1 C与圆 2 C内含； 4.2.3 直线与圆的方程的应用直线与圆的方程的应用 1、利用平面直角坐标系解决直线与圆的位置关系； 2、过程与方法 用坐标法解决几何问题的步骤： 第一步：建立适当的平面直角坐标系，用坐标和方程表示问题中的
21、几何元素，将平面几何问题转化为 代数问题； 第二步：通过代数运算，解决代数问题； 第三步：将代数运算结果“翻译”成几何结论 4.3.1 空间直角坐标系空间直角坐标系 1、 点 M 对应着唯一确定的有序实数组),(zyx，x、y、z分别是 P、 Q、 R 在x、 y、z轴上的坐标 2、有序实数组),(zyx，对应着空间直角坐标系中的一点 3、空间中任意点 M 的坐标都可以用有序实数组),(zyx来表示，该数组叫做点 M 在此空间直角坐标系中 的坐标，记 M),(zyx，x叫做点 M 的横坐标，y叫做点 M 的纵坐 标，z叫做点 M 的竖坐标。 4.3.2 空间两点间的距离公式空间两点间的距离公式 1、空间中任意一点),( 1111 zyxP到点),( 2222 zyxP之间的距离公式 2 21 2 21 2 2121 )()()(zzyyxxPP O y x M M R P Q O y z x M P1 P2 N M1 N2 N1 M2 H
