1、专题 01 函数的图象与性质及其应用 【压轴综述】【压轴综述】 纵观近几年的高考命题，函数图象和性质及其应用问题，常常出现在压轴题的位置，考查的类型主要有： 1.分段函数的图象与性质问题，往往通过分类讨论，将函数在不同定义域内的图象进行刻画或讨论，有时借 助导数这一工具进行研究； 2.函数的零点问题，根据函数的零点情况，讨论参数的范围是高考的重点和难点函数零点问题常常涉及 零点个数问题、零点所在区间问题及零点相关的代数式取值问题，解决的途径常以数形结合的思想，通过 化归与转化灵活转化问题； 3.抽象函数问题，由于抽象函数表现形式抽象，对学生思维能力考查的起点较高，使得此类问题成为函数 内容的难
2、点之一，解决此类问题时，需要准确掌握函数的性质，熟知我们所学的基本初等函数，将抽象函 数问题转化为具体函数问题； 4. 函数性质的综合应用问题，函数性质包括奇偶性、单调性、对称性、周期性等，对函数性质的熟练掌握 与刻画是解决函数综合题目的必然要求； 5.函数与不等式的综合问题，主要有解不等式、及根据不等式确定参数(范围)问题.函数的图象与不等式，往 往涉及数形结合思想、转化与化归思想； 6.函数中的新定义问题. 【压轴典例】【压轴典例】 例 1(2021 安徽淮北市 高三)设 22 543 ,1 2 23,1 1 xaaxa x f x xx x ，若 f x的最小值为 0f， 则a的值为(
3、) A0 B1 或 4 C1 D4 例 2(2021 江苏泰州市 高三期末)已知定义在 R 上的奇函数 ( )f x满足( )(6)f xf x ，且当03x时， 2 2 log(1),01 ( ) 2(2) ,13 axx f x xx ，其中 a为常数，则(2019)(2020)(2021)fff的值为( ) A2 B2 C 1 2 D 1 2 例 3(2020 济南市历城第二中学高三期中)设函数 2 2 ,2f xmin xxx 其中, ,min x y z表示 , ,x y z中的最小者.下列说法错误的是( ) A函数 f x为偶函数 B当 1,x时，有 2f xf x C当xR时，
4、ffxfx D当4,4x 时， 2fxfx 例 4.(2020天津高考T9)已知函数f(x)=若函数g(x)=f(x)-(kR)恰有 4 个零点,则k 的取值范围是 ( ) A.(-,- )(2,+) B.(-,- )(0,2) C.(-,0)(0,2) D.(-,0)(2,+) 例 5. 【2018 年理新课标 I 卷】 已知函数 若 g(x)存在 2个零点， 则 a的取值范围是 A. 1，0) B. 0，+) C. 1，+) D. 1，+) 例 6.(2020全国卷文科T10)设函数 f(x)=x 3- ,则 f(x) ( ) A.是奇函数,且在(0,+)单调递增 B.是奇函数,且在(0,
5、+)单调递减 C.是偶函数,且在(0,+)单调递增 D.是偶函数,且在(0,+)单调递减 例 7.(2020全国卷理科T9)设函数 f(x)=ln|2x+1|-ln|2x-1|,则 f(x) ( ) A.是偶函数,且在单调递增 B.是奇函数,且在单调递减 C.是偶函数,且在单调递增 D.是奇函数,且在单调递减 例 8.【2019 年高考全国卷理数】设函数( )f x的定义域为 R，满足(1)2 ( )f xf x，且当(0,1x时， ( )(1)f xx x 若对任意(,xm ，都有 8 ( ) 9 f x ，则 m 的取值范围是( ) A 9 , 4 B 7 , 3 C 5 , 2 D 8
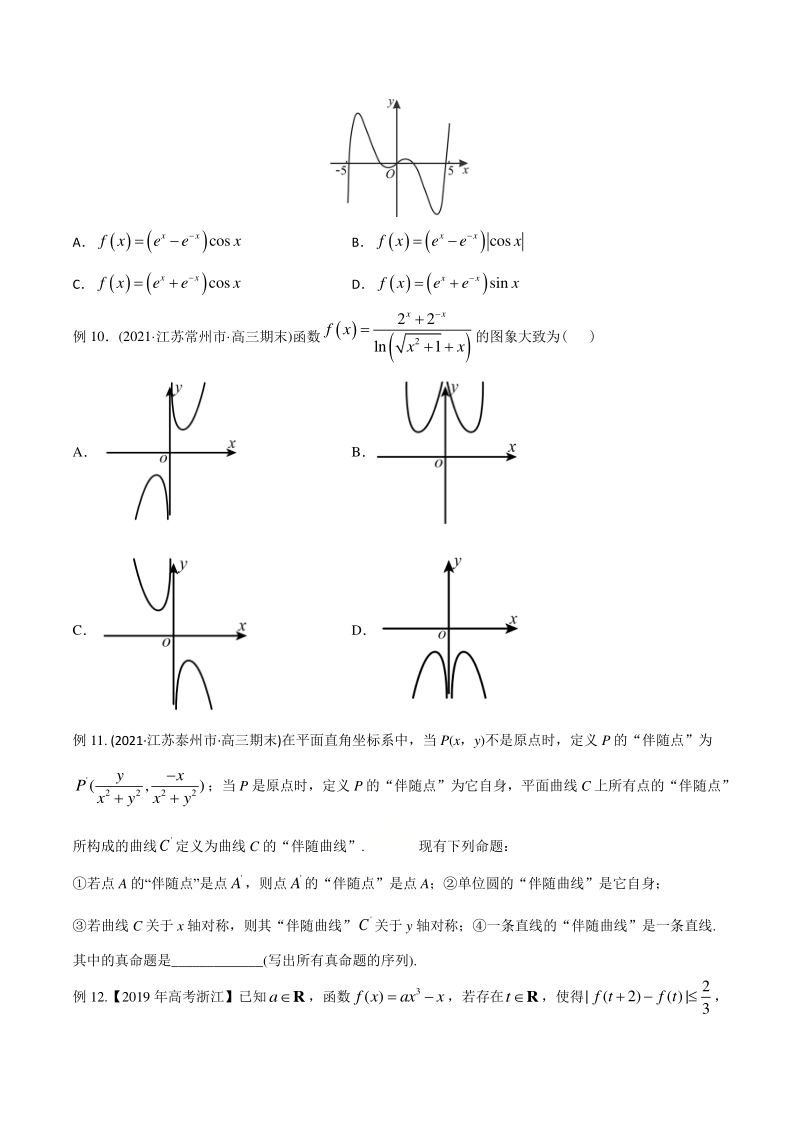
6、, 3 例 9(2021 全国高三专题练习)某函数的部分图象如图所示，则该函数的解析式可能是( ) A cos xx f xeex B cos xx f xeex C cos xx f xeex D sin xx fxeex 例 10(2021 江苏常州市 高三期末)函数 2 22 ln1 xx f x xx 的图象大致为( ) A B C D 例 11. (2021 江苏泰州市 高三期末)在平面直角坐标系中，当 P(x，y)不是原点时，定义 P 的“伴随点”为 2222 (,) yx P xyxy ；当 P 是原点时，定义 P 的“伴随点”为它自身，平面曲线 C 上所有点的“伴随点” 所构成
7、的曲线 C定义为曲线 C 的“伴随曲线”.现有下列命题： 若点 A 的“伴随点”是点 A，则点 A的“伴随点”是点 A；单位圆的“伴随曲线”是它自身； 若曲线 C 关于 x 轴对称，则其“伴随曲线” C关于 y 轴对称；一条直线的“伴随曲线”是一条直线. 其中的真命题是_(写出所有真命题的序列). 例 12.【2019 年高考浙江】已知aR，函数 3 ( )f xaxx，若存在tR，使得 2 |(2)( )| 3 f tf t， 则实数a的最大值是_. 例 13(2020 上海市建平中学高三期中)已知函数 11 22,1 21,1 xx x f x xx ，则关于x的不等式 10f xf x的
8、解集为_ 【压轴训练】【压轴训练】 1(2021 陕西榆林市 高三一模)已知定义在 R上的偶函数 ( )f x满足(2)( )fxf x ，且 ( )f x在( 1,0) 上 递减.若 1 2 5af ，( ln2)bf， 3 log 18cf，则 a，b，c的大小关系为( ) Aac b Bcba Cabc Dbac 2.【2018 年全国卷 II 理】已知是定义域为的奇函数,满足.若， 则( ) A B C D 3(2021 山东高三专题练习)定义域和值域均为 , a a 的函数( )yf x和( )yg x的图象如图所示，其中 0,0abac，给出下列四个结论正确结论的是( ) A方程
9、( )0f g x 有且仅有三个解 B方程 ( )0g f x有且仅有三个解 C方程 ( ) 0g g x 有且仅有一个解 D方程 ( )0f f x有且仅有九个解 4 (多选)(2020 济南市历城第二中学高三期中)设函数 2 2 ,2f xmin xxx 其中, ,min x y z表示 , ,x y z中的最小者.下列说法正确的有( ) A函数 f x为偶函数 B当 1,x时，有 2f xf x C当xR时， ffxfx D当4,4x 时， 2fxfx 5(2021 全国高三专题练习)函数 cosln 2 xx f xxee 的图象大致为( ) A B C D 6.若直角坐标系内 A、B
10、 两点满足：(1)点 A、B 都在 f(x)的图像上；(2)点 A、B 关于原点对称，则称点对(A， B)是函数 f(x)的一个“姊妹点对”(点对(A，B)与(B，A)可看作一个“姊妹点对”。已知函数 f(x)= 2 2 (0) 2 (0) x xx x x e ，则 f(x)的“姊妹点对”有( ) A.1 个 B.2 个 C.3 个 D.4 个 7.【安徽省六安市舒城中学】已知定义在 R 上的函数满足且在上是增函数， 不等式对任意恒成立，则实数 的取值范围是( ) A B C D 8(2020 山西高三期中)已知函数 53 32f xxxx ，若 24f af a，则实数 a的取值范围 是(
11、 ) A,1 B,2 C1, D2, 9(2021 天津高三期末)已知函数 2 (3),0 ( ) 2 ,0 k xx f x xk x ，若函数 g xfxf x有且只有四个不 同的零点，则实数 k 的取值范围是( ) A( , 4) B(4,) C( ,0)(4,) D(,4)(4,) 10. (2021 安徽淮北市 高三)已知函数 1, 0 ( ) ln ,0 x xex f x exx x ，则函数( ) |( )| 1g xf x零点的个数为( ) A3 B4 C5 D6 11.(2020 江西吉安市 高三其他模拟)已知函数 32 lg1f xxxx，若 12320afaf ，则实数
12、a的取值范围是_. 12(2021 福建高三其他模拟)函数 ( )f x 的定义域为 1,1) ，其图象如图所示.函数 ( )g x 是定义域为R的奇 函数，满足 (2)( )0gxg x ，且当 (0,1)x 时， ( )( )g xf x .给出下列三个结论： (0)0g ；函数 ( )g x 在( 1,5) 内有且仅有3个零点；不等式 ()0fx 的解集为 10 xx .其中，正确结论的序号 是_. 13.【2019 年高考北京理数】设函数 ee xx f xa (a 为常数)若 f(x)为奇函数，则 a=_；若 f(x) 是 R 上的增函数，则 a 的取值范围是_ 14(2020 黑龙
13、江哈尔滨市 哈师大附中高三)已知函数 ( )f x是定义域为R的奇函数，且当 0 x时， 2 2 log,02 ( ) 1 47,2 2 xx f x xxx ，若函数( )(01)yf xaa有六个零点，分别记为 123456 ,x x x x x x， 则 123456 xxxxxx的取值范围是_. 15. 【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)高三】已知函数， 若对任意， 总存在， 使得成立， 则实数 的值为_ 16.(2021 上海高三专题练习)双曲线 2 2 1 3 x y绕坐标原点O旋转适当角度可以成为函数 ( )f x的图象，关 于此函数 ( )f x有如下四个命题： ( )f x是奇函数； ( )f x的图象过点 3 3 (,) 22 或 33 (,) 22 ； ( )f x 的值域是 33 (, ,) 22 ； 函数 ( )yf xx 有两个零点；则其中所有真命题的序号为_.
