1、2021 年辽年辽辽宁省沈阳市于洪区辽宁省沈阳市于洪区中考数学第一次分流考试卷中考数学第一次分流考试卷 一、选择题： （每小题一、选择题： （每小题 2 分，共分，共 20 分）分） 12 的绝对值是（ ） A2 B C D2 2下列四个数中，最小的是（ ） A1 B C0 D2 3在平面直角坐标系中，点 P（2，3）关于原点对称的点的坐标是（ ） A （2，3） B （2，3） C （2，3） D （3，2） 4开学伊始，我市开设了大连教育数字课堂，全市约 630000 名学生同上开学第一课数 630000 用科学记 数法表示为（ ） A6.3104 B6.3105 C0.63104 D63
2、104 5将一块直角三角尺 ABC 按如图所示的方式放置，其中点 A、C 分别落在直线 a、b 上，若 ab，1 62，则2 的度数为（ ） A28 B30 C38 D62 6下列计算正确的是（ ） A3a2a22 B （3a3）26a6 C （a2）2a24 Da3a2a5 7一次抛掷两枚相同的硬币，则这两枚硬币都是正面向上的概率是（ ） A B C D 8某医药厂两年前生产 1t 某种药品的成本是 5000 元，随着生产技术的进步，现在生产 1t 该种药品的成本 是 3000 元设该种药品生产成本的年平均下降率为 x，则下列所列方程正确的是（ ） A50002（1x）3000 B5000（
3、1x）23000 C5000（12x）3000 D5000（1x2）3000 9如图，矩形 ABCD 的对角线 AC、BD 相交于点 O，E 是边 BC 的中点，AO，AD4，则 OE 的长为 （ ） A1 B C2 D 10若二次函数 yax2+bx+c（a0）的自变量 x 与函数值 y 的部分对应值如表： x 2 1 0 1 2 y 8 3 0 1 0 则当 x4 时，函数值为（ ） A1 B0 C3 D8 二、填空题（每小题二、填空题（每小题 3 分，共分，共 18 分）分） 11不等式 2x4 的解集是 12如图，某商场大厅自动扶梯 AB 的长为 12m，它与水平面 AC 的夹角BAC
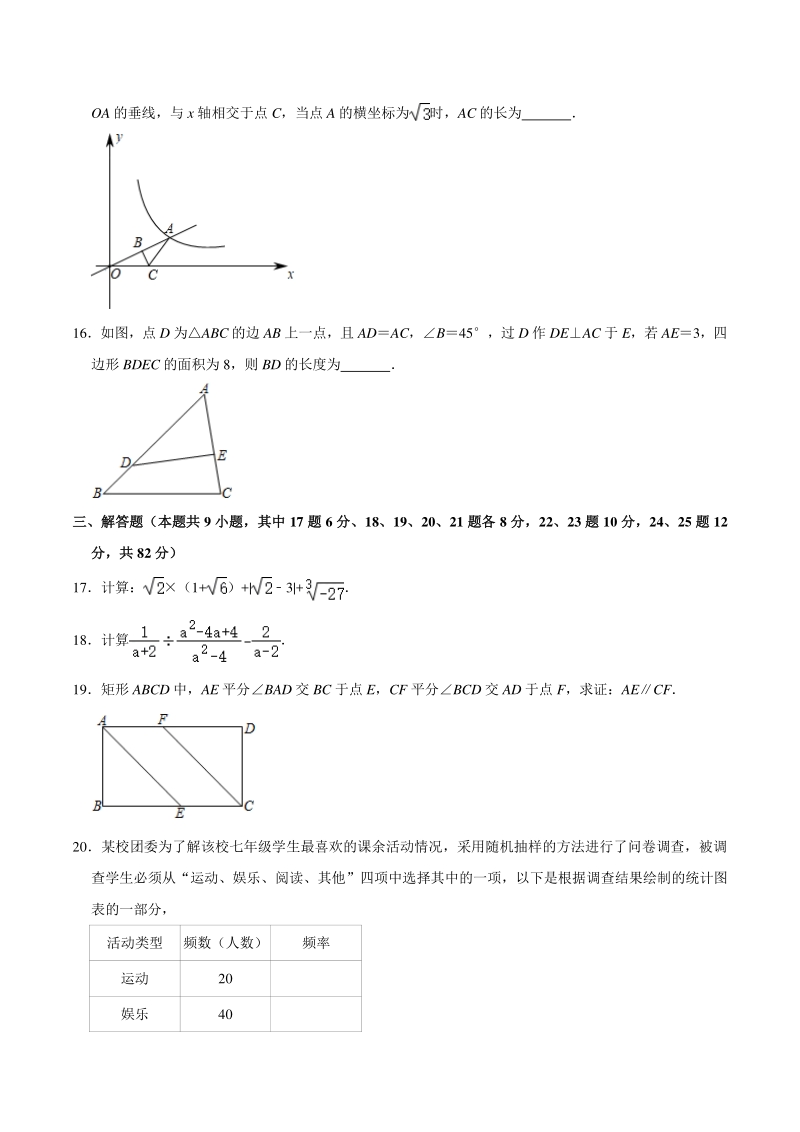
4、30，则大厅两层之间的 高度 BC 为 m 13 某校男子排球队队员的年龄分布为： 13岁3人， 14岁6人， 15岁3人， 则这些队员的平均年龄为 岁 14 “圆材埋壁”是我国古代数学名著九章算术中的一个问题： “今有圆材，埋在壁中，不知大小以 锯锯之，深一寸，锯道长一尺问：径几何？”转化为现在的数学语言就是：如图，AB 是O 的直径， 弦 CDAB，垂足为 E，AE1 寸，CD10 寸，则直径 AB 的长为 寸 15如图，函数 y（x0）的图象与直线 ykx（k0）相交于点 A，点 B 是 OA 的中点，过点 B 作 OA 的垂线，与 x 轴相交于点 C，当点 A 的横坐标为时，AC 的长
5、为 16如图，点 D 为ABC 的边 AB 上一点，且 ADAC，B45，过 D 作 DEAC 于 E，若 AE3，四 边形 BDEC 的面积为 8，则 BD 的长度为 三、解答题（本题共三、解答题（本题共 9 小题，其中小题，其中 17 题题 6 分、分、18、19、20、21 题各题各 8 分，分，22、23 题题 10 分，分，24、25 题题 12 分，共分，共 82 分）分） 17计算：（1+）+|3|+ 18计算 19矩形 ABCD 中，AE 平分BAD 交 BC 于点 E，CF 平分BCD 交 AD 于点 F，求证：AECF 20某校团委为了解该校七年级学生最喜欢的课余活动情况，
6、采用随机抽样的方法进行了问卷调查，被调 查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项，以下是根据调查结果绘制的统计图 表的一部分， 活动类型 频数（人数） 频率 运动 20 娱乐 40 阅读 其他 0.1 根据以上图表信息，解答下列问题： （1）在被调查的学生中，最喜欢“运动”的学生人数为 人，最喜欢“娱乐”的学生人数占被调 查学生人数的百分比为 % （2）本次调查的样本容量是 ，最喜欢“其他”的学生人数为 人 （3）若该校七年级共有 360 名学生，试估计最喜欢“阅读”的学生人数 21在抗击新冠肺炎疫情期间，市场上防护口罩出现热销某药店用 3000 元购进甲，乙两种不同型号的口
7、 罩共 1100 个进行销售，已知购进甲种口罩与乙种口罩的费用相同，购进甲种口罩单价是乙种口罩单价的 1.2 倍 （1）求购进的甲，乙两种口罩的单价各是多少？ （2） 若甲， 乙两种口罩的进价不变， 该药店计划用不超过 7000 元的资金再次购进甲， 乙两种口罩共 2600 个，求甲种口罩最多能购进多少个？ 22如图，AB、AC 是O 的两条弦，且 ABAC，点 D 是的中点，连接并延长 BD、CD，分别交 AC、 AB 的延长线于点 E、F （1）求证：DFDE； （2）若 BD6，CE8，求O 的半径 23ABC 中，ADBC 于 D，tanB，tanC1，AD6，点 E 沿射线 DC 方
8、向一直运动，将点 E 绕点 D 逆时针旋转 90得到点 F （F 在射线 DA 上） ， 点 G 与点 E 关于点 D 成中心对称 （点 G 在射线 DB 上） ， 连接 GE、EF、FG 得到GEF （1）求 BC 的长； （2）在点 E 的运动过程中，设 DEx，GEF 与ABC 的重叠部分面积为 S，求 S 与 x 的函数关系式 24如图，ABC 是等腰直角三角形，BAC90，ABAC，BDC45，E 是 BD 上的一点，且 BAECBD，AE 交 BC 于点 M，将CBD 沿 BC 翻折得BCF，BF 交 AE 于 G，交 AC 于 H （1）AGF 的度数为 ； （2）探究 BG 与
9、 CD 的数量关系，并证明； （3）若 AGkGM，求的值 25定义：在平面直角坐标系 xOy 中，点 P 的坐标为（x，y） ，当 xm 时，Q 点坐标为（x，y） ；当 x m 时，Q 点坐标为（x，y+2） ，则称点 Q 为点 P 的 m 分变换点（其中 m 为常数） 例如： （2，3） 的 0 分变换点坐标为（2，1） （1）点（5，7）的 1 分变换点坐标为 ；点（1，6）的 1 分变换点在反比例函数 y图象上， 则 k ；若点（a1，5）的 1 分变换点在直线 yx+2 上，则 a （2）若点 P 在二次函数 yx22x3 的图象上，点 Q 为点 P 的 3 分变换点 直接写出点
10、Q 所在函数的解析式； 求点 Q 所在函数的图象与直线 y5 交点坐标； 当4xt 时，点 Q 所在函数的函数值5y6，直接写出 t 的取值范围 （3）点 A（3，1） ，B（2，1） ，若点 P 在二次函数 yx2mx+2 的图象上，点 Q 为点 P 的 m 分变换点当点 Q 所在的函数图象与线段 AB 有两个公共点时，直接写出 m 的取值范围 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题）小题） 12 的绝对值是（ ） A2 B C D2 【分析】根据绝对值是实数轴上的点到原点的距离，可得答案 【解答】解：2 的绝对值是 2 故选：A 2下列四个数中，最小的是
11、（ ） A1 B C0 D2 【分析】根据“正数大于 0，0 大于一切负数，两个负数，绝对值大的而反而小”进行比较即可判定选择 项 【解答】解：因为102， 所以最小的数是1 故选：A 3在平面直角坐标系中，点 P（2，3）关于原点对称的点的坐标是（ ） A （2，3） B （2，3） C （2，3） D （3，2） 【分析】根据“平面直角坐标系中任意一点 P（x，y） ，关于原点的对称点是（x，y） ”解答 【解答】解：根据中心对称的性质，得点 P（2，3）关于原点对称的点的坐标是（2，3） 故选：B 4开学伊始，我市开设了大连教育数字课堂，全市约 630000 名学生同上开学第一课数 63
12、0000 用科学记 数法表示为（ ） A6.3104 B6.3105 C0.63104 D63104 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把 原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同 【解答】解：将 630000 用科学记数法表示为：6.3105 故选：B 5将一块直角三角尺 ABC 按如图所示的方式放置，其中点 A、C 分别落在直线 a、b 上，若 ab，1 62，则2 的度数为（ ） A28 B30 C38 D62 【分析】根据平行线的性质得出31，进而利用互余解答即可 【解答】解：如图， ab
13、， 1362， 2+390， 2903906228， 故选：A 6下列计算正确的是（ ） A3a2a22 B （3a3）26a6 C （a2）2a24 Da3a2a5 【分析】根据幂的乘方、积的乘方、同底数幂的乘法以及合并同类项法则进行计算即可 【解答】解：3a2a22a2，因此选项 A 不符合题意； （3a3）29a6，因此选项 B 不符合题意； （a2）2a24a+4，因此选项 C 不符合题意； a3a2a5，因此选项 D 符合题意； 故选：D 7一次抛掷两枚相同的硬币，则这两枚硬币都是正面向上的概率是（ ） A B C D 【分析】根据题意可以通过树状图写出所有的可能性，从而可以得到两个
14、都是正面向上的概率 【解答】解：由题意可得， 两个都是正面向上的概率为， 故选：B 8某医药厂两年前生产 1t 某种药品的成本是 5000 元，随着生产技术的进步，现在生产 1t 该种药品的成本 是 3000 元设该种药品生产成本的年平均下降率为 x，则下列所列方程正确的是（ ） A50002（1x）3000 B5000（1x）23000 C5000（12x）3000 D5000（1x2）3000 【分析】若这种药品的年平均下降率为 x，根据两年前生产 1 吨某药品的成本是 5000 元，随着生产技术 的进步，现在生产 1 吨药品的成本是 3000 元可列方程 【解答】解：设这种药品的年平均下
15、降率为 x， 5000（1x）23000 故选：B 9如图，矩形 ABCD 的对角线 AC、BD 相交于点 O，E 是边 BC 的中点，AO，AD4，则 OE 的长为 （ ） A1 B C2 D 【分析】根据矩形的性质和三角形中位线的性质以及勾股定理即可得到结论 【解答】解：四边形 ABCD 是矩形， AOCO，AC2AO2，ADC90， CD2， E 是边 BC 的中点， OE 是BCD 的中位线， OECD1， 故选：A 10若二次函数 yax2+bx+c（a0）的自变量 x 与函数值 y 的部分对应值如表： x 2 1 0 1 2 y 8 3 0 1 0 则当 x4 时，函数值为（ ）
16、A1 B0 C3 D8 【分析】根据函数的对称性求得函数的对称轴为直线 x1，所以 x2 和 x4 关于函数对称轴对称， 据此即可求解 【解答】解：当 x0 和 x2 时的函数值相同， 函数的对称轴为直线 x1， x2 和 x4 关于函数对称轴对称， x2 时的函数值为 8， x4 时的函数值为 8， 故选：D 二填空题（共二填空题（共 6 小题）小题） 11不等式 2x4 的解集是 x2 【分析】两边都除以 2 即可得 【解答】解：2x4， x2， 故答案为：x2 12如图，某商场大厅自动扶梯 AB 的长为 12m，它与水平面 AC 的夹角BAC30，则大厅两层之间的 高度 BC 为 6 m
17、 【分析】在 RtABC 中，利用三角函数解答即可 【解答】解；在 RtABC 中，BAC30，AB12m， BCm， 故答案为：6 13某校男子排球队队员的年龄分布为：13 岁 3 人，14 岁 6 人，15 岁 3 人，则这些队员的平均年龄为 14 岁 【分析】根据题意和题目中的数据，可以计算出这些队员的平均年龄，本题得以解决 【解答】解：14（岁） ， 即这些队员的平均年龄为 14 岁， 故答案为：14 14 “圆材埋壁”是我国古代数学名著九章算术中的一个问题： “今有圆材，埋在壁中，不知大小以 锯锯之，深一寸，锯道长一尺问：径几何？”转化为现在的数学语言就是：如图，AB 是O 的直径，
18、 弦 CDAB，垂足为 E，AE1 寸，CD10 寸，则直径 AB 的长为 26 寸 【分析】连接 OC设圆的半径是 x 寸，在直角OCE 中，OCx 寸，OEx1，在直角OCE 中利用 勾股定理即可列方程求得半径，进而求得直径 AB 的长 【解答】解：连接 OC设圆的半径是 x 寸，在直角OCE 中，OCx 寸，OE（x1）寸， OC2OE2+CE2， 则 x2（x1）2+25， 解得：x13 则 AB21326（寸） 故答案为：26 15如图，函数 y（x0）的图象与直线 ykx（k0）相交于点 A，点 B 是 OA 的中点，过点 B 作 OA 的垂线，与 x 轴相交于点 C，当点 A 的
19、横坐标为时，AC 的长为 【分析】先将 x代入 y，求出 y，得到 A 点坐标，设 C 点坐标为（x，0） ，则 OCx再根据 BC 是线段 OA 的垂直平分线，得出 OCAC，依此列出方程得出即可 【解答】解：函数 y（x0）的图象过点 A，点 A 的横坐标为， 当 x时，y1， A（，1） 设 C 点坐标为（x，0） ，则 OCx BC 是线段 OA 的垂直平分线， OCAC， x2（x）2+（10）2， 解得 x， ACOC， 故答案为： 16如图，点 D 为ABC 的边 AB 上一点，且 ADAC，B45，过 D 作 DEAC 于 E，若 AE3，四 边形 BDEC 的面积为 8，则
20、BD 的长度为 2 【分析】过点 C 作 CFAB 于点 F，根据全等三角形的性质得到 AFAE3，推出BFC 是等腰直角三 角形，根据三角形的面积公式得到 BFCF4，根据勾股定理得到 ADAC5，于是得 到结论 【解答】解：过点 C 作 CFAB 于点 F， DEAC， AFCBFCAED90， AA，ADAC， ADEACF（AAS） ， AFAE3， SBFC四边形 BDEC 的面积8， B45， BFC 是等腰直角三角形， BFCFBF28， BFCF4， ADAC5， DF2， BD2， 故答案为：2 三解答题三解答题 17计算：（1+）+|3|+ 【分析】直接利用二次根式的混合运
21、算法则以及绝对值的性质、立方根的定义分析得出答案 【解答】解：原式+2+33 2 18计算 【分析】根据分式的运算法则即可求出答案 【解答】解：原式 19矩形 ABCD 中，AE 平分BAD 交 BC 于点 E，CF 平分BCD 交 AD 于点 F，求证：AECF 【分析】由矩形的性质的 ADBC，BADBCD90，由平行线的性质得出AEBDAE，由角 平分线定义得出AEBDAEBCF，即可得出 AECF 【解答】证明：四边形 ABCD 是矩形， ADBC，BADBCD90， AEBDAE， AE 平分BAD，CF 平分BCD， DAEBAD45，BCFBCD45， AEBDAEBCF， AE
22、CF 20某校团委为了解该校七年级学生最喜欢的课余活动情况，采用随机抽样的方法进行了问卷调查，被调 查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项，以下是根据调查结果绘制的统计图 表的一部分， 活动类型 频数（人数） 频率 运动 20 娱乐 40 阅读 其他 0.1 根据以上图表信息，解答下列问题： （1）在被调查的学生中，最喜欢“运动”的学生人数为 20 人，最喜欢“娱乐”的学生人数占被调查 学生人数的百分比为 40 % （2）本次调查的样本容量是 100 ，最喜欢“其他”的学生人数为 10 人 （3）若该校七年级共有 360 名学生，试估计最喜欢“阅读”的学生人数 【分析】 （
23、1）从统计表和统计图中可以直接得出答案； （2）从统计图表中可得，最喜欢“娱乐”的学生 40 人占被调查学生人数的百分比为 40%，可求出调查 人数； （3）求出样本中， “阅读”学生占调查人数的百分比即可 【解答】解： （1）从统计图表中，可得最喜欢“运动”的有 20 人，最喜欢“娱乐”的学生人数占被调查 学生人数的百分比为 40%， 故答案为：20，40； （2）4040%100（人） ，1000.110（人） ， 故答案为：100，10； （3）360108（人） ， 答：该校七年级 360 名学生中最喜欢“阅读”的学生有 108 人 21在抗击新冠肺炎疫情期间，市场上防护口罩出现热销某
24、药店用 3000 元购进甲，乙两种不同型号的口 罩共 1100 个进行销售，已知购进甲种口罩与乙种口罩的费用相同，购进甲种口罩单价是乙种口罩单价的 1.2 倍 （1）求购进的甲，乙两种口罩的单价各是多少？ （2） 若甲， 乙两种口罩的进价不变， 该药店计划用不超过 7000 元的资金再次购进甲， 乙两种口罩共 2600 个，求甲种口罩最多能购进多少个？ 【分析】 （1）设乙种口罩的单价为 x 元，则甲种口罩的单价为 1.2x 元，根据数量总价单价，即可得 出关于 x 的分式方程，解之经检验后即可得出结论； （2）设该药店购进甲种口罩 a 只，则购进乙种口罩（2600a）只，根据总价单价数量结合
25、进货总 价不超过 7000 元，即可得出关于 a 的一元一次不等式，解之取其中的最大值即可得出结论 【解答】解： （1）300021500（元） 设乙种口罩的单价为 x 元，则甲种口罩的单价为 1.2x 元， 依题意，得：， 解得：x2.5， 经检验，x2.5 是原方程的解，且符合题意， 1.2x3 答：甲种口罩的单价为 3 元，乙种口罩的单价为 2.5 元 （2）设该药店购进甲种口罩 a 只，则购进乙种口罩（2600a）只， 依题意，得：3a+2.5（2600a）7000， 解得：a1000 答：甲种口罩最多购进 1000 只 22如图，AB、AC 是O 的两条弦，且 ABAC，点 D 是的
26、中点，连接并延长 BD、CD，分别交 AC、 AB 的延长线于点 E、F （1）求证：DFDE； （2）若 BD6，CE8，求O 的半径 【分析】 （1）连接 AD，通过证得CADBAD（SAS） ，得出ACDABD，进而根据 ASA 证得 CEDBFD（ASA） ，即可证得结论； （2）根据圆内接四边形的性质证得ABD90，从而证得 AD 是直径，根据勾股定理求得 ED，进而 求得 AB，然后根据勾股定理求得 AD，从而求得半径 【解答】 （1）证明：连接 AD， 点 D 是的中点， CADBAD， CDBD， 在CAD 和BAD 中， ， CADBAD（SAS） ， ACDABD， DCE
27、DBF， 在CED 和BFD 中， ， CEDBFD（ASA） ， DFDE； （2）解：四边形 ABDC 是圆内接四边形， DBFACD， ACDABD， ABDDBF， ABD90， ECDABD90， AD 是O 的直径， CDBD6，CE8， DE10， EB10+616， 在 RtABE 中，AB2+BE2AE2， 设 ABACx，则 x2+162（x+8）2， 解得 x12， AB12， 在 RtABD 中，AB2+BD2AD2， AD6， O 的半径为 3 23ABC 中，ADBC 于 D，tanB，tanC1，AD6，点 E 沿射线 DC 方向一直运动，将点 E 绕点 D 逆时
28、针旋转 90得到点 F （F 在射线 DA 上） ， 点 G 与点 E 关于点 D 成中心对称 （点 G 在射线 DB 上） ， 连接 GE、EF、FG 得到GEF （1）求 BC 的长； （2）在点 E 的运动过程中，设 DEx，GEF 与ABC 的重叠部分面积为 S，求 S 与 x 的函数关系式 【分析】 （1）解直角三角形求出 BD，CD 即可解决问题； （2）分三种情形：如图 1 中，当 0 x6 时，重叠部分是EFG如图 2 中，当 6x12 时，重 叠部分是五边形 ACGM当 x12 时，重叠部分是ABC分别求解即可解决问题； 【解答】解： （1）ADBC， ADBADC90， t
29、anB，tanC1，AD6， CDAD6，BD2AD12， BCBD+CD18 （2）如图 1 中，当 0 x6 时，重叠部分是EFG，S2xxx2 如图 2 中，当 6x12 时，重叠部分是五边形 ACGM 作 BKGF 交 DF 的延长线于 K，作 MHBC 于 H易知：AB6，DBDK12， FMBK， ， ， AM（x6） ， MHAD， ， ， MH12x， SSABCSBMG618（12x）（12x）x2+12x18 当 x12 时，重叠部分是ABC，S54， 综上所述，S 24如图，ABC 是等腰直角三角形，BAC90，ABAC，BDC45，E 是 BD 上的一点，且 BAECB
30、D，AE 交 BC 于点 M，将CBD 沿 BC 翻折得BCF，BF 交 AE 于 G，交 AC 于 H （1）AGF 的度数为 45 ； （2）探究 BG 与 CD 的数量关系，并证明； （3）若 AGkGM，求的值 【分析】 （1）证明MBGBAM，利用三角形的外角的性质解决问题即可 （2）结论 CDBG作 BTBF 交 AE 的延长线于 T证明 BGBT，推出ABTBCD，可得 ，可得结论 （3）设 GMm，则 AGkm，利用相似三角形的性质，求出 CH，可得结论 【解答】解： （1）由翻折的性质可知，CBDCBF， CBDBAE， BAECBF， ABAC，BAC90， ABC45，
31、AGFABG+BAG， AGFABG+CBFABC45， 故答案为：45 （2）结论 CDBG 理由：作 BTBF 交 AE 的延长线于 T GBT90，BGTAGF45， TBGT45， BGBT， DT，BATDBC， ABTBCD， ， ABAC，BAC90， BCAB， ， CDBTBG （3）AGkGM， 可以假设 GMm，则 AGkm， MBGMAB，BMGAMB， BMGAMB， ， BM2MGAMm（m+km）m2（1+k） ， BMm， ABMBCH45，BAMCBH， ABMBCH， ， CHBMm， 25定义：在平面直角坐标系 xOy 中，点 P 的坐标为（x，y） ，当
32、 xm 时，Q 点坐标为（x，y） ；当 x m 时，Q 点坐标为（x，y+2） ，则称点 Q 为点 P 的 m 分变换点（其中 m 为常数） 例如： （2，3） 的 0 分变换点坐标为（2，1） （1）点（5，7）的 1 分变换点坐标为 （5，7） ；点（1，6）的 1 分变换点在反比例函数 y 图象上，则 k 4 ；若点（a1，5）的 1 分变换点在直线 yx+2 上，则 a 8 （2）若点 P 在二次函数 yx22x3 的图象上，点 Q 为点 P 的 3 分变换点 直接写出点 Q 所在函数的解析式； 求点 Q 所在函数的图象与直线 y5 交点坐标； 当4xt 时，点 Q 所在函数的函数值
33、5y6，直接写出 t 的取值范围 （3）点 A（3，1） ，B（2，1） ，若点 P 在二次函数 yx2mx+2 的图象上，点 Q 为点 P 的 m 分变换点当点 Q 所在的函数图象与线段 AB 有两个公共点时，直接写出 m 的取值范围 【分析】 （1）根据新定义进行解答便可； （2）分两种情况：x3；x3根据 m 分变换点的定义求出 Q 点的坐标，进而便可写出点 Q 所 在函数的解析式； 把 y5 代入点 Q 所在的函数解析式中，便可求得交点坐标； 根据函数的性质进行解答便可； （3）分两种情况：xm 和 xm 求得点 Q 所在的函数解析式，再根据函数的性质求得函数图象与线段 AB 的两个公
34、共点，画出函数图象，可得结论 【解答】解： （1）51， 点（5，7）的 1 分变换点坐标为（5，7） ； 11， 点（1，6）的 1 分变换点为（1，4） ， 点（1，6）的 1 分变换点在反比例函数 y图象上， k1（4）4； 当 a11，即 a2 时，点（a1，5）的 1 分变换点为（1a，5） ， 点（a1，5）的 1 分变换点在直线 yx+2 上， 51a+2， a8， 当 a11，即 a2 时，点（a1，5）的 1 分变换点为（1a，3） ， 点（a1，5）的 1 分变换点在直线 yx+2 上， 31a+2， a6， （不合题意舍去） 故答案为： （5，7） ；4；8； （2）设
35、Q（m，n） ， 点 Q 为点 P 的 3 分变换点， 当m3，即 m3 时，P（m，n） ， nm2+2m3， nm22m+3， 点 Q 所在函数的解析式为 yx22x+3（x3） ； 当m3，即 m3 时，P（m，2n） ， 2nm2+2m3， nm22m+5， 点 Q 所在函数的解析式为 yx22x+5（m3） 故点 Q 所在函数的解析式为 yx22x+3（x3）或 yx22x+5（x3） 把 y5 代入 yx22x+3（x3）得x22x+35， 解得，x4，或 x2（舍） ； 把 y5 代入 yx22x+5（x3）得，x22x+55， 解得，x1（舍弃或 x1+， 综上，点 Q 所在函
36、数的图象与直线 y5 交点坐标为（1+，5）或（4，5） yx22x+3（x+1）2+4（x3） ， y 的最大值为 46，且当 x3 时，y 随 x 的增大而减小， 令 y5，得 yx22x+35（x3） ， 解得，x2（舍） ，x4（舍） ； yx22x+5（x+1）2+6（x3） ， y 的最大值为 6，当1x3 时，y 随 x 的增大而减小，当 x1 时，y 随 x 的增大而增大， 令 y5 时，得x22x+55， 解得，x1+，x1， 当 y0 时，x22x+50， 解得，x1+或1（舍弃） 当1+t1+时，点 Q 所在函数的函数值5y6； 综上，当4xt 时，点 Q 所在函数的函数值5y6，其 t 的取值范围是1+t1+； （3）设 P（x，x2mx+2） ，则 Q 是函数解析式为 y，函数图象， 如图所示（图中实线部分） 当 m0 时，抛物线 y（x+）2+2 交 y 轴于（0，1）时，m或（舍弃） ， 此时函数 Q 与线段 AB 只有一个交点， 当（2+）2+41 时，满足条件， 解得，m2或 m2+， 观察图象可知，满足条件的 m 的值为：2+m 当 m0 时，观察图象可知，不存在满足条件的 m 的值 综上所述，满足条件的 m 的值为：2+m
