 2019-2020学年重庆市九龙坡区二校联考七年级上期末数学试卷(含答案详解)
2019-2020学年重庆市九龙坡区二校联考七年级上期末数学试卷(含答案详解)
《2019-2020学年重庆市九龙坡区二校联考七年级上期末数学试卷(含答案详解)》由会员分享,可在线阅读,更多相关《2019-2020学年重庆市九龙坡区二校联考七年级上期末数学试卷(含答案详解)(19页珍藏版)》请在七七文库上搜索。
1、 2019-2020 学年重庆市九龙坡区学年重庆市九龙坡区二校联考二校联考七年级(上)期末数学试卷七年级(上)期末数学试卷 一、选择题: (本大题一、选择题: (本大题 12 个小题,每小题个小题,每小题 3 分,共分,共 36 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑. 1 (3 分)下列有理数中最小的是( ) A1 B2 C3 D0 2 (3 分)如果以学校为起点,沿龙腾大道向东走记为
2、正,向西走记为负小江放学后从学校出发,先走了 50 米去公交站,又走了+60 米离开公交车站去的士招呼点,此时小江离学校的距离是( ) A10 米 B20 米 C30 米 D50 米 3 (3 分)如图是一个正方体的表面展开图,则图中“是”这一面的对面的字是( ) A我 B爱 C育 D才 4 (3 分)近似数 2.70 所表示的准确数 a 的取值范围是( ) A2.695a2.705 B2.65a2.75 C2.695a2.705 D2.65a2.75 5 (3 分)下列各式,运算正确的是( ) A5a3a2 B2a+3b5ab C7a+a7a2 D10ab25b2a5ab2 6 (3 分)下
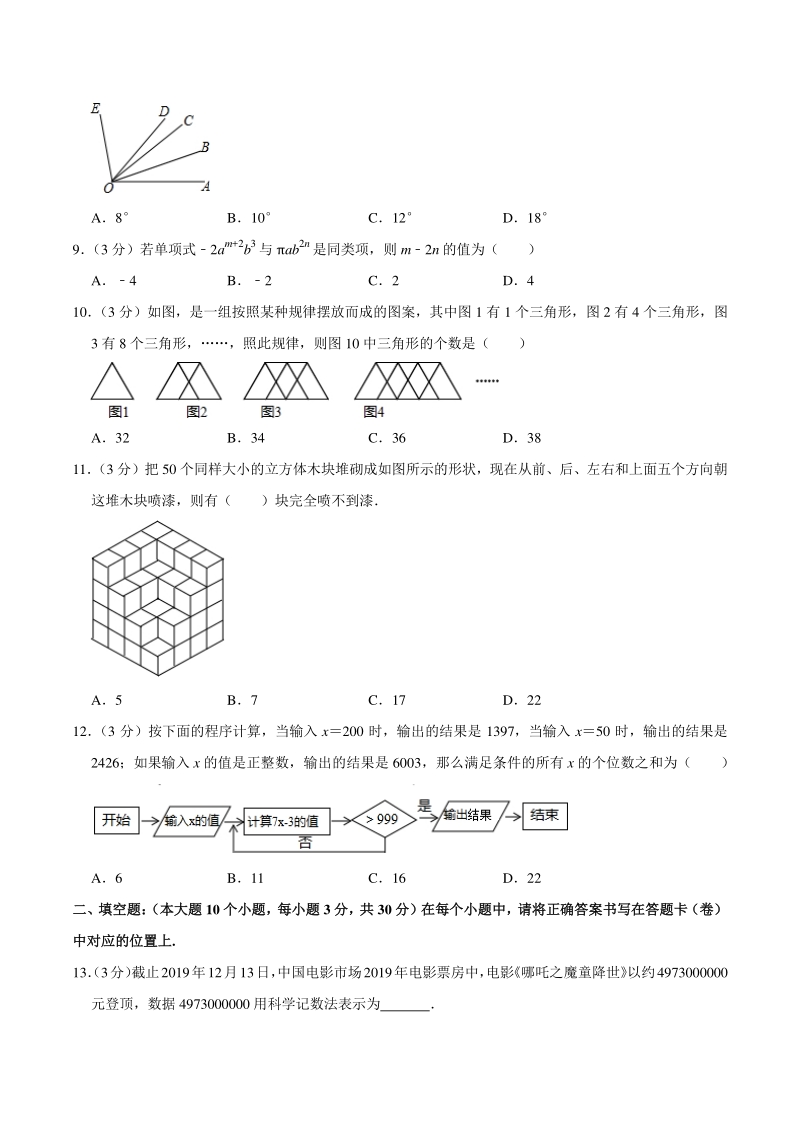
3、列各数(2)2、24、0、|2|、(2) 、 (2)3中,负数的个数是( ) A1 个 B2 个 C3 个 D4 个 7 (3 分)下列说法中,正确的是( ) A过两点有且只有一条直线 B连接两点的线段叫做两点间的距离 C两点之间,直线最短 D到线段两个端点距离相等的点叫做线段的中点 8 (3 分)如图,已知AOB26,AOE120,OB 平分AOC,OD 平分AOE,则COD 的度数 为( ) A8 B10 C12 D18 9 (3 分)若单项式2am+2b3与 ab2n是同类项,则 m2n 的值为( ) A4 B2 C2 D4 10 (3 分)如图,是一组按照某种规律摆放而成的图案,其中图
4、 1 有 1 个三角形,图 2 有 4 个三角形,图 3 有 8 个三角形,照此规律,则图 10 中三角形的个数是( ) A32 B34 C36 D38 11 (3 分)把 50 个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左右和上面五个方向朝 这堆木块喷漆,则有( )块完全喷不到漆 A5 B7 C17 D22 12 (3 分)按下面的程序计算,当输入 x200 时,输出的结果是 1397,当输入 x50 时,输出的结果是 2426;如果输入 x 的值是正整数,输出的结果是 6003,那么满足条件的所有 x 的个位数之和为( ) A6 B11 C16 D22 二、填空题: (本大
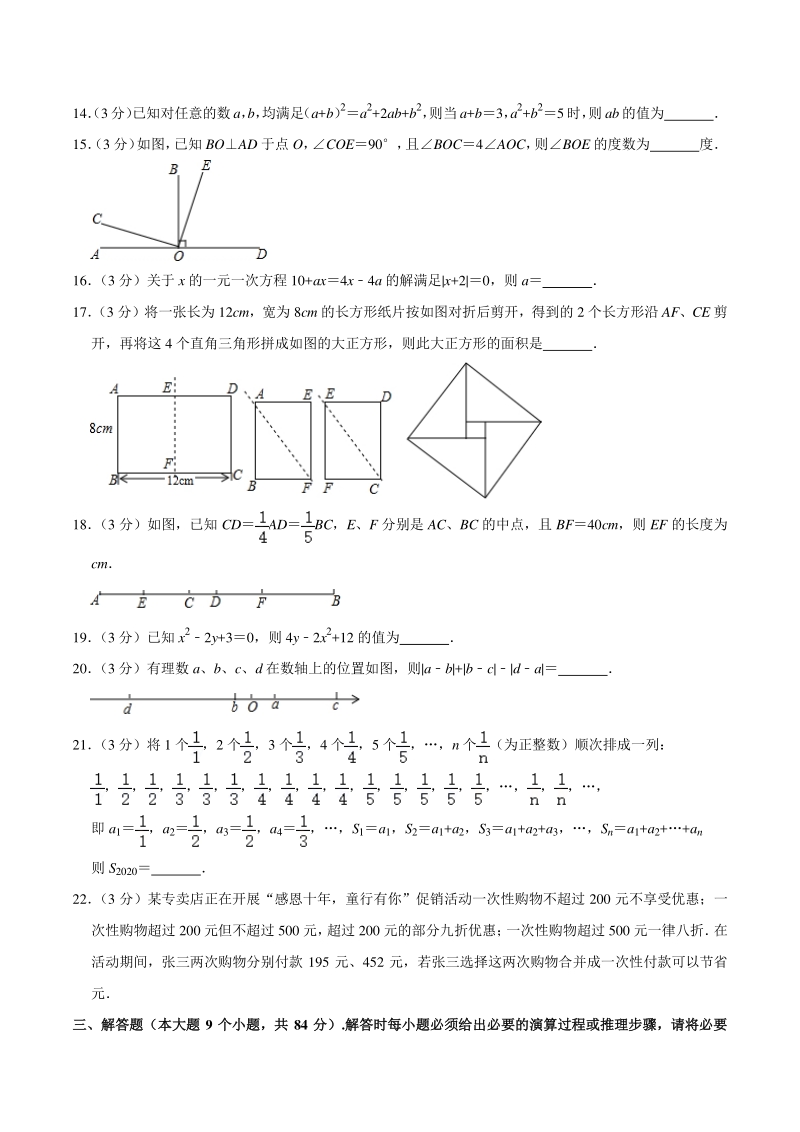
5、题二、填空题: (本大题 10 个小题,每小题个小题,每小题 3 分,共分,共 30 分)在每个小题中,请将正确答案书写在答题卡(卷)分)在每个小题中,请将正确答案书写在答题卡(卷) 中对应的位置上中对应的位置上. 13(3分) 截止2019年12月13日, 中国电影市场2019年电影票房中, 电影 哪吒之魔童降世 以约4973000000 元登顶,数据 4973000000 用科学记数法表示为 14(3分) 已知对任意的数a, b, 均满足 (a+b) 2a2+2ab+b2, 则当a+b3, a2+b25时, 则ab的值为 15(3 分) 如图, 已知 BOAD 于点 O, COE90, 且
6、BOC4AOC, 则BOE 的度数为 度 16 (3 分)关于 x 的一元一次方程 10+ax4x4a 的解满足|x+2|0,则 a 17 (3 分)将一张长为 12cm,宽为 8cm 的长方形纸片按如图对折后剪开,得到的 2 个长方形沿 AF、CE 剪 开,再将这 4 个直角三角形拼成如图的大正方形,则此大正方形的面积是 18 (3 分)如图,已知 CDADBC,E、F 分别是 AC、BC 的中点,且 BF40cm,则 EF 的长度为 cm 19 (3 分)已知 x22y+30,则 4y2x2+12 的值为 20 (3 分)有理数 a、b、c、d 在数轴上的位置如图,则|ab|+|bc|da
7、| 21 (3 分)将 1 个,2 个,3 个,4 个,5 个,n 个(为正整数)顺次排成一列: , 即 a1,a2,a3,a4,S1a1,S2a1+a2,S3a1+a2+a3,Sna1+a2+an 则 S2020 22 (3 分)某专卖店正在开展“感恩十年,童行有你”促销活动一次性购物不超过 200 元不享受优惠;一 次性购物超过 200 元但不超过 500 元, 超过 200 元的部分九折优惠; 一次性购物超过 500 元一律八折 在 活动期间,张三两次购物分别付款 195 元、452 元,若张三选择这两次购物合并成一次性付款可以节省 元 三、解答题(本大题三、解答题(本大题 9 个小题,
8、共个小题,共 84 分)分).解答时每小题必须给出必要的演算过程或推理步骤,请将必要解答时每小题必须给出必要的演算过程或推理步骤,请将必要 的解题过程书写在答题卡(卷)中对应的位置上的解题过程书写在答题卡(卷)中对应的位置上. 23 (12 分)计算: (1)6.14+(2)(5.86)(+) (2)24()622 (3) (1)2020+18()+24()36(+1)02019 (4) ()201832021+(2)32.5|3| 24 (9 分)如图,已知点 O 在直线 AB 上,COOD,OE 平分AOD,BOD10,求COE 的度数 25 (9 分)如图,AB10cm,线段 BD4cm
9、,线段 AC7cm,E 是线段 BC 的中点,FD2AF,求 EF 的 长 26 (9 分) (1)化简:2(2x23xy4y2)3(x22xy) ; (2)先化简,再求值:4mn22mn23(6m2n4mn2)+10m2n2(mn2m2n) ,其中(m+2) 2+|n+1|0 27 (9 分)解下列一元一次方程: (1)2(4x3)5(2x1)7 (2)1 28 (9 分)重庆育才中学需要为老校友们订制 80 周年纪念吉祥物“陶娃” ,原计划订 750 份,每份 50 元, 订制公司表示:如果多订,可以优惠根据校庆当天前来的校友数量,学校最终订了 1000 份,并按原价 八折购买,但订制公司
10、获得了同样的利润 (1)求订制公司生产每套“陶娃”的成本; (2)求订制公司获得的利润 29 (9 分)材料一:我们可以将任意三位数记为, (其中 a、b、c 分别表示该数的百位数字,十位数字 和个位数字,且 a0) 显然100a+10b+c 材料二:若一个三位数的百位数字,十位数字和个位数字均不为 0,则称之为“生数” ,比如 123 就是一 个“生数” ,将“生数”的三个数位上的数字交换顺序,可产生出 5 个新的“生数” ,比如由 123 可以产 生出 132、213、231、312、321 这 5 个新“生数” ,将这 6 个数相加,得到的和 1332 称为由“生数”123 生成的“完全
11、数” 问题: (1)求证:任意一个“完全数”都可以被 6 整除; (2)若一个四位正整数(1m9,m 是整数)是由一个“生数”(1x9,1y9, x、y 是整数)产生的“完全数” ,请求出这个“生数” 30 (9 分)苏宁易购为了提高某品牌家电的销售量,2019 年 10 月份开始对销售员采取新奖励办法已知 销售员小李在新奖励办法出台前一个月共售出这种家电的 A 型和 B 型共 200 台,新奖励办法出台后的第 一个月售出这两种型号的家电共 246 台,其中 A 型和 B 型家电的销售量分别比新奖励办法出台前一个月 增长 25%和 20% (1)在新奖励办法出台后第一个月里,该销售员分别销售了
12、 A 型和 B 型家电多少台? (2)若 A 型家电每台售价为 3000 元,B 型家电每台售价为 5000 元新奖励办法是:每销售一台 A 型家 电按每台 A 型家电售价的 a%给予奖励,每销售一台 B 型家电按每台 B 型家电售价的 5%给予奖励 新奖 励办法出台后的第二个月,A 型家电的销售量比出台后的第一个月增加了 10%;而 B 型家电受到某问题 零件召回的影响,销售量比出台后的第一个月减少了a%,新奖励办法出台后的第二个月该销售员共得 到奖励金额 117000 元,求 a 的值 31 (9 分)数轴上有 A、B、C 三个点,分别表示有理数24、10、10,两条动线段 PQ 和 MN
13、,PQ2, MN4,如图,线段 MN 以每秒 1 个单位的速度从点 B 开始一直向右匀速运动,线段 PQ 同时以每秒 3 个单位的速度从点 A 开始向右匀速运动,当点 Q 运动到 C 时,线段 PQ 立即以相同的速度返回,当点 P 运动到点 A 时,线段 PQ、MN 立即同时停止运动,设运动时间为 t 秒(整个运动过程中,线段 PQ 和 MN 保持长度不变,且点 P 总在点 Q 的左边,点 M 总在点 N 的左边) (1)当 t 为何值时,点 Q 和点 N 重合? (2)在整个运动过程中,线段 PQ 和 MN 重合部分长度能否为 1,若能,请求出此时点 P 表示的数;若 不能,请说明理由 参考
14、答案与试题解析参考答案与试题解析 一、选择题: (本大题一、选择题: (本大题 12 个小题,每小题个小题,每小题 3 分,共分,共 36 分)在每个小题的下面,都给出了代号为分)在每个小题的下面,都给出了代号为 A、B、C、 D 的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑. 1 (3 分)下列有理数中最小的是( ) A1 B2 C3 D0 【解答】解:2103, 最小的是2 故选:B 2 (3 分)如果以学校为起点,沿龙腾大道向东走记为正,向西走记为负小江放学后从学校出发,先走了
15、 50 米去公交站,又走了+60 米离开公交车站去的士招呼点,此时小江离学校的距离是( ) A10 米 B20 米 C30 米 D50 米 【解答】解:50+6010, 此时,小江离学校的距离为 10, 故选:A 3 (3 分)如图是一个正方体的表面展开图,则图中“是”这一面的对面的字是( ) A我 B爱 C育 D才 【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形, “我”与“是”是相对面, “育”与“人”是相对面, “们”与“才”是相对面 故选:A 4 (3 分)近似数 2.70 所表示的准确数 a 的取值范围是( ) A2.695a2.705 B2.65a2.75 C2.6
16、95a2.705 D2.65a2.75 【解答】解:近似数 2.70 所表示的准确值 a 的取值范围是 2.695a2.705 故选:A 5 (3 分)下列各式,运算正确的是( ) A5a3a2 B2a+3b5ab C7a+a7a2 D10ab25b2a5ab2 【解答】解:5a3a2a,选项 A 不符合题意; 2a+3b5ab,选项 B 不符合题意; 7a+a8a,选项 C 不符合题意; 10ab25b2a5ab2,选项 D 符合题意 故选:D 6 (3 分)下列各数(2)2、24、0、|2|、(2) 、 (2)3中,负数的个数是( ) A1 个 B2 个 C3 个 D4 个 【解答】解:(
17、2)24;2416;|2|2;(2)2; (2)38, 负数有24、|2|、 (2)3共 3 个 故选:C 7 (3 分)下列说法中,正确的是( ) A过两点有且只有一条直线 B连接两点的线段叫做两点间的距离 C两点之间,直线最短 D到线段两个端点距离相等的点叫做线段的中点 【解答】解:A、过两点有且只有一条直线,故符合题意; B、连接两点的线段的长度叫做两点的距离,故不符合题意; C、两点之间,线段最短,故不符合题意; D、在线段上且到线段两个端点距离相等的点叫做线段的中点,故不符合题意; 故选:A 8 (3 分)如图,已知AOB26,AOE120,OB 平分AOC,OD 平分AOE,则CO
18、D 的度数 为( ) A8 B10 C12 D18 【解答】解:OB 平分AOC,AOB26, AOC2AOB52, OD 平分AOE,AOE120, AODAOE60, CODAODAOC60528 则COD 的度数为 8 故选:A 9 (3 分)若单项式2am+2b3与 ab2n是同类项,则 m2n 的值为( ) A4 B2 C2 D4 【解答】解:单项式2am+2b3与 ab2n是同类项, m+21,2n3, 解得 m1,n, m2n134 故选:A 10 (3 分)如图,是一组按照某种规律摆放而成的图案,其中图 1 有 1 个三角形,图 2 有 4 个三角形,图 3 有 8 个三角形,
19、照此规律,则图 10 中三角形的个数是( ) A32 B34 C36 D38 【解答】解:第一个图案有三角形 1 个, 第二图案有三角形 1+34 个, 第三个图案有三角形 1+3+48 个, 第四个图案有三角形 1+3+4+412, 第 n 个图案有三角形 4(n1)个, 第 10 个图中三角形的个数是 4(101)36 故选:C 11 (3 分)把 50 个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左右和上面五个方向朝 这堆木块喷漆,则有( )块完全喷不到漆 A5 B7 C17 D22 【解答】解:50 个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左、右和上面五
20、个 方向朝这堆木块喷漆, 从下面数第 1 层有 12 个立方体木块会喷到漆, 从下数第 2 层有 12 个立方体木块都喷到漆, 从下面数第 3 层有 12 个立方体木块都会喷到漆, 从下数第 4 层有 7 个立方体木块都会喷到漆 一点儿漆都喷不到的木块个数是:50(12+12+12+7)7(块) 故选:B 12 (3 分)按下面的程序计算,当输入 x200 时,输出的结果是 1397,当输入 x50 时,输出的结果是 2426;如果输入 x 的值是正整数,输出的结果是 6003,那么满足条件的所有 x 的个位数之和为( ) A6 B11 C16 D22 【解答】解:当一次输出时,60037x3

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2019 2020 学年 重庆市 九龙坡区 联考 年级 期末 数学试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-178645.html