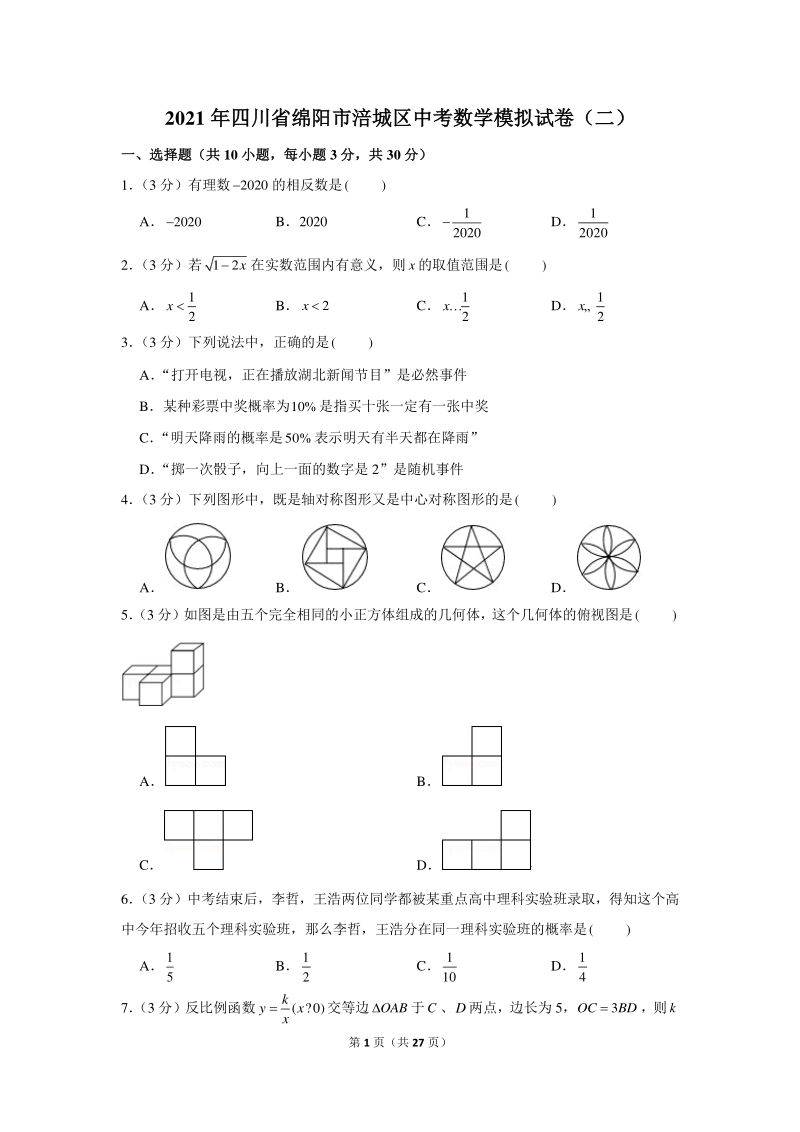
1、 第 1 页（共 27 页） 2021 年四川省绵阳市涪城区中考数学模拟试卷（二）年四川省绵阳市涪城区中考数学模拟试卷（二） 一、选择题（共一、选择题（共 10 小题，每小题小题，每小题 3 分，共分，共 30 分）分） 1 （3 分）有理数2020的相反数是( ) A2020 B2020 C 1 2020 D 1 2020 2 （3 分）若12x在实数范围内有意义，则x的取值范围是( ) A 1 2 x B2x C 1 2 x D 1 2 x 3 （3 分）下列说法中，正确的是( ) A “打开电视，正在播放湖北新闻节目”是必然事件 B某种彩票中奖概率为10%是指买十张一定有一张中奖 C “
2、明天降雨的概率是50%表示明天有半天都在降雨” D “掷一次骰子，向上一面的数字是 2”是随机事件 4 （3 分）下列图形中，既是轴对称图形又是中心对称图形的是( ) A B C D 5 （3 分）如图是由五个完全相同的小正方体组成的几何体，这个几何体的俯视图是( ) A B C D 6 （3 分）中考结束后，李哲，王浩两位同学都被某重点高中理科实验班录取，得知这个高 中今年招收五个理科实验班，那么李哲，王浩分在同一理科实验班的概率是( ) A 1 5 B 1 2 C 1 10 D 1 4 7 （3 分）反比例函数( ?0) k yx x 交等边OAB于C、D两点，边长为 5，3OCBD，则k
3、 第 2 页（共 27 页） 的值( ) A 9 3 8 B 9 3 4 C153 4 D 15 3 4 8 （3 分）一个容器有进水管和出水管，每分钟的进水量和出水量是两个常数从某时刻开 始4min内只进水不出水，从第4min到第24min内既进水又出水，从第24min开始只出水不 进水，容器内水量y（单位：)L与时间x（单位：)min之间的关系如图所示，则图中a的 值是( ) A32 B34 C36 D38 9 （3 分）如图，AB为半圆O的直径，BCAB且BCAB，射线BD交半圆O的切线于 点E，DFCD交AB于F，若2AEBF，2 10DF ，则O的半径长为( ) A 3 13 2 B
4、4 2 C 5 5 2 D 3 10 2 10 （3 分）观察等式： 23 2222； 234 22222； 2345 222222 已知 按一定规律排列的一组数： 50 2、 51 2、 52 2、 99 2、 100 2若 50 2a，用含a的式子表示 这组数的和是( ) A 2 22aa B 2 222aa C 2 2aa D 2 2aa 二、填空题（共二、填空题（共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 第 3 页（共 27 页） 11 （3 分） 2 ( 5) 12 （3 分）疫情期间小隆和爸爸、妈妈、爷爷、奶奶测量体温（单位：C) ，结果分别为 36.2、
5、37.1、36.5、37.1、36.6，其中中位数是 13 （3 分）计算 22 23mn mnmn 的结果是 14 （3 分）如图，在平行四边形ABCD中，E、F是对角线AC上两点，AEEFCD， 90ADF，63BCD，则ADE的大小为 15 （3 分）定义a、b、 c为二次函数 2 (0)yaxbxc a的特征数，下面给出特征数为 2m，1m，1m 的函数的一些结论： 当3m 时， 函数图象的顶点坐标是 1 (3，8) 3 ； 当0m 时，函数图象截x轴所得的线段长度大于 3 2 ；当0m 时，函数在 1 4 x 时，y 随x的增大而减小；当0m 时，函数图象经过同一个点，正确的结论是
6、16（3 分） 如图， 在ABC中， 点D，E分别为AB，AC边上一点， 且BECD，CDBE 若 30A，1BD ，2 3CE ，则四边形CEDB的面积为 三、解答题（共三、解答题（共 8 题，共题，共 72 分）分） 17 （8 分）计算： 354 22 (3) aaaa 18（8 分） 如图， 点A、B、C、D在一条直线上，CE与BF交于点G，1A ，/ /CEDF， 求证：EF 第 4 页（共 27 页） 19 （8 分）某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情 况，随机调查了若干名学生，根据调查数据进行整理，绘制了如下的不完整统计图 请你根据以上的信息，回
7、答下列问题： （1）本次共调查了 名学生，其中最喜爱戏曲的有 人；在扇形统计图中，最喜爱体 育的对应扇形的圆心角大小是 （2）根据以上统计分析，估计该校 2000 名学生中最喜爱新闻的人数 20 （8 分）以下各图均是由边长为 1 的小正方形组成的网格，图中的点A、B、C、D均 在格点上 （1）在图中，:PC PB （2）利用网格和无刻度的直尺作图，保留痕迹，不写作法 如图，在AB上找一点P，使3AP 如图，在BD上找一点P，使APBCPD 21 （8 分）如图，在ABC中，90C，BAC的平分线交BC于点D，点O在AB上， 以OA为半径的O经过点D，与AB交于点E （1）求证： 2 BDBE
8、 BA； （2）若 2 2 cos 3 B ，4AE ，求CD 第 5 页（共 27 页） 22 （10 分） 某商店销售一种商品， 经市场调查发现： 该商品的周销售量y（件)是售价x（元 /件）的一次函数，其售价、周销售量、周销售利润w（元)的三组对应值如表： 售价x（元/件） 50 60 80 周销售量y（件) 100 80 40 周销售利润w（元) 1000 1600 1600 注：周销售利润周销售量（售价进价） （1）求y关于x的函数解析式（不要求写出自变量的取值范围） ； 该商品进价是 元/件； 当售价是 元/件时， 周销售利润最大， 最大利润是 元 （2）由于某种原因，该商品进价提
9、高了m元/件(0)m，物价部门规定该商品售价不得超 过 65 元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系若周 销售最大利润是 1400 元，求m的值 23 （10 分）如图，ABC中，CACB （1）当点D为AB上一点， 1 2 AMDN 如图 1，若点M、N分别在AC、BC上，ADBD，问：DM与DN有何数量关系？证 明你的结论； 如图 2，若 1 4 AD BD ，作2MDN，使点M在AC上，点N在BC的延长线上，完成图 2，判断DM与DN的数量关系，并证明； （2）如图 3，当点D为AC上的一点，ABDN ，/ /CNAB，2CD ，1AD ，直 接写出AB
10、CN的积 24 （12 分）在平面直角坐标系中，抛物线 2 1: 1Cyaxbx的最高点为点( 1,0)D ，将 1 C 第 6 页（共 27 页） 左移 1 个单位，上移 1 个单位得到拋物线 2 C，点P为 2 C的顶点 （1）求抛物线C的解析式； （2）若过点D的直线l与抛物线 2 C只有一个交点，求直线l的解析式； （3） 直线yxc与抛物线 2 C交于D、B两点， 交y轴于点A， 连接AP， 过点B作BCAP 于点C，点Q为 2 C上PB之间的一个动点，连接PQ交BC于点E，连接BQ并延长交AC于 点F，试说明：()FCACEC为定值 第 7 页（共 27 页） 2021 年四川省绵
11、阳市涪城区中考数学模拟试卷（二）年四川省绵阳市涪城区中考数学模拟试卷（二） 参考答案与试题解析参考答案与试题解析 一、选择题（共一、选择题（共 10 小题，每小题小题，每小题 3 分，共分，共 30 分）分） 1 （3 分）有理数2020的相反数是( ) A2020 B2020 C 1 2020 D 1 2020 【解答】解：有理数2020的相反数是：2020 故选：B 2 （3 分）若12x在实数范围内有意义，则x的取值范围是( ) A 1 2 x B2x C 1 2 x D 1 2 x 【解答】解：由题意得，1 20 x， 解得 1 2 x 故选：D 3 （3 分）下列说法中，正确的是(
12、) A “打开电视，正在播放湖北新闻节目”是必然事件 B某种彩票中奖概率为10%是指买十张一定有一张中奖 C “明天降雨的概率是50%表示明天有半天都在降雨” D “掷一次骰子，向上一面的数字是 2”是随机事件 【解答】解：A、打开电视，正在播放湖北新闻节目”是随机事件，故A不符合题意； B、某种彩票中奖概率为10%是指买十张有可能中奖，故B不符合题意； C、明天降雨的概率是50%表示明天有可能降雨” ，故C不符合题意； D、 “掷一次骰子，向上一面的数字是 2”是随机事件，故D符合题意； 故选：D 4 （3 分）下列图形中，既是轴对称图形又是中心对称图形的是( ) A B C D 【解答】解
13、：A、是轴对称图形，不是中心对称图形，故此选项不合题意； B、不是轴对称图形，是中心对称图形，故此选项不合题意； 第 8 页（共 27 页） C、是轴对称图形，不是中心对称图形，故此选项不合题意； D、既是轴对称图形，又是中心对称图形，故此选项符合题意 故选：D 5 （3 分）如图是由五个完全相同的小正方体组成的几何体，这个几何体的俯视图是( ) A B C D 【解答】解：根据俯视图是从上面看所得到的图形，可知这个几何体的俯视图C中的图形， 故选：C 6 （3 分）中考结束后，李哲，王浩两位同学都被某重点高中理科实验班录取，得知这个高 中今年招收五个理科实验班，那么李哲，王浩分在同一理科实验
14、班的概率是( ) A 1 5 B 1 2 C 1 10 D 1 4 【解答】解：画树状图如下： 由树状图知，共有 25 种等可能结果，其中李哲，王浩分在同一理科实验班的有 5 种结果， 所以李哲，王浩分在同一理科实验班的概率为 51 255 ， 故选：A 7 （3 分）反比例函数( ?0) k yx x 交等边OAB于C、D两点，边长为 5，3OCBD，则k 的值( ) 第 9 页（共 27 页） A 9 3 8 B 9 3 4 C153 4 D 15 3 4 【解答】解：过点C作CEx轴于点E，过点D作DFx轴于点F， 设BDa，则3OCa， 在Rt OCE中，60COE， 则 3 2 OE
15、a， 3 3 2 CEa， 则点C坐标为 3 ( 2 a， 3 3 ) 2 a， 在Rt BDF中，BDa，60DBF， 则 1 2 BFa， 3 2 DFa， 则点D的坐标为 1 ( 5 2 a ， 3 ) 2 a， 将点C的坐标代入反比例函数解析式可得： 2 9 3 4 ka， 将点D的坐标代入反比例函数解析式可得： 2 5 33 24 kaa， 则 22 9 35 33 424 aaa， 解得： 1 1a ， 2 0a （舍去） ， 故 9 3 4 k 故选：B 8 （3 分）一个容器有进水管和出水管，每分钟的进水量和出水量是两个常数从某时刻开 始4min内只进水不出水，从第4min到第
16、24min内既进水又出水，从第24min开始只出水不 第 10 页（共 27 页） 进水，容器内水量y（单位：)L与时间x（单位：)min之间的关系如图所示，则图中a的 值是( ) A32 B34 C36 D38 【解答】解：由图象可知，进水的速度为：2045( /)L min， 出水的速度为：5(3520)(164)3.75( /)L min， 第 24 分钟时的水量为：20(53.75)(244)45( )L， 24453.7536a 故选：C 9 （3 分）如图，AB为半圆O的直径，BCAB且BCAB，射线BD交半圆O的切线于 点E，DFCD交AB于F，若2AEBF，2 10DF ，则O
17、的半径长为( ) A 3 13 2 B4 2 C 5 5 2 D 3 10 2 【解答】解：连接AD，CF，作CHBD于H，如图所示： AB是直径， 90ADB， 90ADFBDF，90DABDBA， 90BDFBDC，90CBDDBA， ADFBDC ，DABCBD ， ADFBDC， ADAFDF BDBCCD ， 第 11 页（共 27 页） 90DAEDAB ，90EDAE， EDAB， ADEBDA， AEAD ABBD ， AEAF ABBC ，即 AEAB AFBC ， ABBC， AEAF， 2AEBF， 3BCABBF， 设BFx，则2AEx，3ABBCx， 22 13BEA
18、EABx， 22 10CFBFBCx， 由切割线定理得： 2 AEED BE， 22 (2 )4 13 1313 AEx EDx BEx ， 9 13 13 BDBEED， CHBD， 90BHC，CBHBCHCBHABE ， CBHABE ， 90BAEBHC ， BCHEBA， BHCHBC AEABBE ，即 3 2313 BHCHx xxx ， 解得： 6 13 13 BHx， 9 13 13 CHx， 3 13 13 DHBDBHx， 2222 90 13 CDCHDHx， DFCD， 222 CDDFCF，即 222 90 (2 10)( 10 ) 13 xx， 第 12 页（共
19、27 页） 解得：13x ， 3 13AB， O的半径长为 3 13 2 ； 故选：A 10 （3 分）观察等式： 23 2222； 234 22222； 2345 222222 已知 按一定规律排列的一组数： 50 2、 51 2、 52 2、 99 2、 100 2若 50 2a，用含a的式子表示 这组数的和是( ) A 2 22aa B 2 222aa C 2 2aa D 2 2aa 【解答】解： 23 2222； 234 22222； 2345 222222； 231 222222 nn ， 50515299100 22222 231002349 (2222)(2222 ) 10150
20、 (22)(22) 10150 22， 50 2a， 10150 22 2(2 )22a， 原式 2 2aa 故选：C 二、填空题（共二、填空题（共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 第 13 页（共 27 页） 11 （3 分） 2 ( 5) 5 【解答】解：原式255 故答案为：5 12 （3 分）疫情期间小隆和爸爸、妈妈、爷爷、奶奶测量体温（单位：C) ，结果分别为 36.2、37.1、36.5、37.1、36.6，其中中位数是 36.6 【解答】解：将数据重新排列为 36.2、36.5、36.6、37.1、37.1， 所以这组数据的中位数为 36.6， 故
21、答案为：36.6 13 （3 分）计算 22 23mn mnmn 的结果是 1 mn 【解答】解：原式 2()3 ()()()() mnmn mn mnmn mn 223 ()() mnmn mn mn ()() mn mn mn 1 mn 故答案为： 1 mn 14 （3 分）如图，在平行四边形ABCD中，E、F是对角线AC上两点，AEEFCD， 90ADF，63BCD，则ADE的大小为 21 【解答】解：设ADEx， AEEF，90ADF， DAEADEx ， 1 2 DEAFAEEF， AEEFCD， DECD， 2DCEDECx ， 四边形ABCD是平行四边形， / /ADBC， 第
22、14 页（共 27 页） DAEBCAx ， 63DCEBCDBCAx ， 263xx， 解得：21x ， 即21ADE； 故答案为：21 15 （3 分）定义a、b、 c为二次函数 2 (0)yaxbxc a的特征数，下面给出特征数为 2m，1m，1m 的函数的一些结论： 当3m 时， 函数图象的顶点坐标是 1 (3，8) 3 ； 当0m 时，函数图象截x轴所得的线段长度大于 3 2 ；当0m 时，函数在 1 4 x 时，y 随x的增大而减小；当0m 时，函数图象经过同一个点，正确的结论是 【解答】解：把3m 代入，得6a ，4b ，2c ，函数解析式为 2 642yxx ， 利用顶点公式可
23、以求出顶点为 1 (3， 8) 3 ，正确； 函数 2 2(1)( 1)ymxm xm 与x轴两交点坐标为(1,0)， 1 ( 2 m m ，0)， 当0m 时， 1313 1() 2222 m mm ，正确； 当0m 时，函数 2 2(1)( 1)ymxm xm 开口向下，对称轴 111 444 x m ， x可能在对称轴左侧也可能在对称轴右侧，错误； 22 2(1)( 1)(21)1ymxm xmmxxx ，若使函数图象经过同一点，0m 时， 应使 2 210 xx ，可得 1 1x ， 2 1 2 x ，当1x 时，0y ，当 1 2 x 时， 3 2 y ，则 函数一定经过点(1,0)
24、和 1 ( 2 ， 3) 2 ，正确 故答案为： 16（3 分） 如图， 在ABC中， 点D，E分别为AB，AC边上一点， 且BECD，CDBE 若 30A，1BD ，2 3CE ，则四边形CEDB的面积为 19 4 第 15 页（共 27 页） 【解答】解：分别过点C、E两点作CKAB，EHAB 交AB于点K和点H，设CKx，如图所示： CDBE， 90BMD， 90EBHCDB， 同理可得：90EBHBEH， CDBBEH ， 又CKAB，EHAB， 90CKDBHE ， 在CKD和BHE中， CDKBEH CKDBHE CDBE ， ()CKDBHE AAS ， DKEH， 又Rt AK
25、C中，30A， 2ACx，3AKx， 又ACAEEC，2 3CE ， 22 3AEx， 第 16 页（共 27 页） 3EHDKx， 又DKDBBK，1BD ， 31BKx， 又AKAHBHBK， 43BHx， 又BHCK， 43xx， 解得： 43 2 x ， 43 3 2 DKx ， 在Rt CDK中，由勾股定理得： 22222 434319 ()() 222 CDCKDK ， 1 2 CEDB SCD BE 四边形 2 1 2 CD 119 22 19 4 故答案为 19 4 三、解答题（共三、解答题（共 8 题，共题，共 72 分）分） 17 （8 分）计算： 354 22 (3) a
26、aaa 【解答】解：原式 882 (9)aaa 82 10aa 6 10a 18（8 分） 如图， 点A、B、C、D在一条直线上，CE与BF交于点G，1A ，/ /CEDF， 求证：EF 第 17 页（共 27 页） 【解答】证明一：1A ， / /AEBF， 2E / /CEDF， 2F ， EF 证明二：/ /CEDF， ACED ， 1A ， 1801801ACEAD， 又180EACEA，1801FD， EF 19 （8 分）某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情 况，随机调查了若干名学生，根据调查数据进行整理，绘制了如下的不完整统计图 请你根据以上的信息
27、，回答下列问题： （1）本次共调查了 50 名学生，其中最喜爱戏曲的有 人；在扇形统计图中，最喜爱 体育的对应扇形的圆心角大小是 （2）根据以上统计分析，估计该校 2000 名学生中最喜爱新闻的人数 【解答】解： （1）本次共调查学生：48%50（人)，最喜爱戏曲的人数为：506%3 （人)； 第 18 页（共 27 页） “娱乐”类人数占被调查人数的百分比为： 18 100%36% 50 ， “体育”类人数占被调查人数的百分比为：18%30%36%6%20%， 在扇形统计图中，最喜爱体育的对应扇形的圆心角大小是36020%72； 故答案为：50，3，72 （2）20008%160（人)， 答
28、：估计该校 2000 名学生中最喜爱新闻的人数约有 160 人 20 （8 分）以下各图均是由边长为 1 的小正方形组成的网格，图中的点A、B、C、D均 在格点上 （1）在图中，:PC PB 1:3 （2）利用网格和无刻度的直尺作图，保留痕迹，不写作法 如图，在AB上找一点P，使3AP 如图，在BD上找一点P，使APBCPD 【解答】解： （1）图 1 中， / /ABCD， 1 3 PCCD PBAB ， 故答案为1:3 （2） 如图 2 所示，点P即为所要找的点； 第 19 页（共 27 页） 如图 3 所示，作点A的对称点A， 连接AC，交BD于点P， 点P即为所要找的点， / /ABC
29、D， APBCPD 21 （8 分）如图，在ABC中，90C，BAC的平分线交BC于点D，点O在AB上， 以OA为半径的O经过点D，与AB交于点E （1）求证： 2 BDBE BA； （2）若 2 2 cos 3 B ，4AE ，求CD 【解答】 （1）证明：连接OD，如图， AD平分BAC， 4BAD ， OAOD， 1OAD ， 14 ， / /ACOD， 90ODBC ， 即3290 ， AE为直径， 90ADE，即1390 ， 12 ， 2BAD ， 而DBEABD， BDEBAD， :BD BABE BD， 第 20 页（共 27 页） 2 BDBE BA； （2）4AE ， 2OD
30、， 在Rt BOD中， 2 2 cos 3 BD B BO ， 设2 2BDx，则3BOx， 22 (3 )(2 2 )ODxxx， 2x， 4 2BD，6BO ， / /ODAC， BDBO CDOA ，即 4 26 2CD ， 4 2 3 CD 22 （10 分） 某商店销售一种商品， 经市场调查发现： 该商品的周销售量y（件)是售价x（元 /件）的一次函数，其售价、周销售量、周销售利润w（元)的三组对应值如表： 售价x（元/件） 50 60 80 周销售量y（件) 100 80 40 周销售利润w（元) 1000 1600 1600 注：周销售利润周销售量（售价进价） （1）求y关于x的
31、函数解析式（不要求写出自变量的取值范围） ； 该商品进价是 40 元/件； 当售价是 元/件时， 周销售利润最大， 最大利润是 元 （2）由于某种原因，该商品进价提高了m元/件(0)m，物价部门规定该商品售价不得超 过 65 元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系若周 第 21 页（共 27 页） 销售最大利润是 1400 元，求m的值 【解答】解： （1）依题意设ykxb， 则有 50100 6080 kb kb 解得： 2 200 k b 所以y关于x的函数解析式为2200yx ； 该商品进价是50100010040， 设每周获得利润 2 :waxbxc 则
32、有 2500501000 3600601600 6400801600 abc abc abc ， 解得： 2 280 8000 a b c ， 22 228080002(70)1800wxxx， 当售价是 70 元/件时，周销售利润最大，最大利润是 1800 元； 故答案为：40，70，1800； （2）根据题意得， 222 1401 (40)( 2200)2(2802 )80002002()601800 22 m wxmxxm xmxmm ， 20 ， 抛物线的开口向下， 65x，w随x的增大而增大， 当65x 时，1400w 最大 ， 即 2 14002 65(2802 ) 65 8000
33、200mm ， 解得：5m 23 （10 分）如图，ABC中，CACB 第 22 页（共 27 页） （1）当点D为AB上一点， 1 2 AMDN 如图 1，若点M、N分别在AC、BC上，ADBD，问：DM与DN有何数量关系？证 明你的结论； 如图 2，若 1 4 AD BD ，作2MDN，使点M在AC上，点N在BC的延长线上，完成图 2，判断DM与DN的数量关系，并证明； （2）如图 3，当点D为AC上的一点，ABDN ，/ /CNAB，2CD ，1AD ，直 接写出AB CN的积 【解答】解： （1）DMDN， 理由如下：当DMAC，DNBC时， CACB， AB ， 在ADM和BDN中，
34、 AB AMDBND ADBD ， ()ADMBDN AAS ， DMDN； 当DM、AC不垂直，DN、BC不垂直时， 如图 1，过D作DPAC于P，DQBC于Q，则DPDQ， 在四边形CPDQ中，90DPCDQC， 180PDQPCQ； 2180PCQA ， 2PDQMDNA ； PDMQDN， 在PDM和QDN中， 第 23 页（共 27 页） PDMQDN DPDQ DPMDQN ， ()PDMQDN ASA ， DMDN； 完成图 2，如图 2 所示， 过D作DPAC于P，DQBC于Q， 90AADP ，90BQDB ， 180AADPBQDB ， 2180AADPQDB ， 2PDQ
35、A ，又2MDNA ， PDQMDN， PDMNDQ，又90DPMDQN， DPMDQN， DMDP DNDQ ， AB ，90DPADQB， APDBQD， DPAD DQDB ， 1 4 DMAD DNDB ， 4DNDM； （2）连接BN， CDBAABDCDNBDN ，BDNA ， CDNABD ， / /CNAB， BCNABC ，又CABCBA ， BCNBDNA ， 点C、D、B、N四点共圆， CDNCBN ， CBNABD ，BCNA ， 第 24 页（共 27 页） ABDCBN， ADAB CNBC ， 3AB CNAD BC 24 （12 分）在平面直角坐标系中，抛物线
36、2 1: 1Cyaxbx的最高点为点( 1,0)D ，将 1 C 左移 1 个单位，上移 1 个单位得到拋物线 2 C，点P为 2 C的顶点 （1）求抛物线C的解析式； （2）若过点D的直线l与抛物线 2 C只有一个交点，求直线l的解析式； （3） 直线yxc与抛物线 2 C交于D、B两点， 交y轴于点A， 连接AP， 过点B作BCAP 于点C，点Q为 2 C上PB之间的一个动点，连接PQ交BC于点E，连接BQ并延长交AC于 点F，试说明：()FCACEC为定值 第 25 页（共 27 页） 【解答】解： （1）抛物线 2 1: 1Cyaxbx的最高点为点( 1,0)D ， 2 1 2 4 0
37、 4 b a ab a ， 1 2 a b ， 抛物线 2 1: 21Cyxx， （2）由（1）知，抛物线 22 1: 21(1)Cyxxx ， 将 1 C向左移 1 个单位，上移 1 一个单位得到抛物线 2 C， 22 (2)143yxxx ， 设过点( 1,0)D 的直线的解析式为ykxb ， 0kb ， bk ， 过点( 1,0)D 的直线的解析式为：ykxk， 抛物线 2 C与过点D的直线只有一个交点， 联立解得， 2 (4)(3)0 xkxk， 2 (4)4(3)0kk， 2k， 过点D的直线的解析式为22yx， 第 26 页（共 27 页） （3）如图， 直线yxc与抛物线 2 C
38、交于点D、B两点，且( 1,0)D ， 1c ， 直线AB的解析式为1yx， (0,1)A， 抛物线 2 2: (2)1Cyx， 顶点( 2,1)P ， / /ACx轴， 2 43yxx， 联立得，( 4, 3)B ， 过点Q作QMAC于点M，过点Q作QNBC于点N， BCAP， 四边形CNQM是矩形， / /QNAC，/ /QMBC， ( 4,1)C， 设点Q的坐标为 2 ( ,43)ttt， 则 2 (2)QMCNt， 4MCQNt ， 2PMt ， 2PC ， 2 4BNtt ，4BC ， 第 27 页（共 27 页） / /QMCE， PQMPEC， QMPM ECPC ， 即 2 (2)2 2 tt EC ， 2(2)ECt ， / /QNFC， QNBN FCBC ， 2 44 4 ttt FC ， 4 t FC ， 4AC ， ()|42(2)| 8 4 t FC ACECt ， 即()FCACEC为定值 8
