 2020-2021学年四川省成都市青羊区石室中学七年级上期末数学试卷(含答案详解)
2020-2021学年四川省成都市青羊区石室中学七年级上期末数学试卷(含答案详解)
《2020-2021学年四川省成都市青羊区石室中学七年级上期末数学试卷(含答案详解)》由会员分享,可在线阅读,更多相关《2020-2021学年四川省成都市青羊区石室中学七年级上期末数学试卷(含答案详解)(25页珍藏版)》请在七七文库上搜索。
1、2020-2021 学年四川省成都市青羊区七年级(上)期末数学试卷学年四川省成都市青羊区七年级(上)期末数学试卷 一、选择题(本大题共一、选择题(本大题共 10 个小题,每小题个小题,每小题 3 分,共分,共 30 分)分) 1 (3 分)8 的相反数是( ) A8 B C D8 2 (3 分)将一个直角三角板绕直角边旋转一周,则旋转后所得几何体是( ) A圆柱 B圆 C圆锥 D三角形 3 (3 分)地球的半径约为 6400000 米,用科学记数法表示为( ) A6.4105 米 B640104 米 C6.4106 米 D64105 米 4 (3 分)下列式子,符合用字母表示数的书写格式的是(
2、 ) Aa3 B2x Ca3 D 5 (3 分)如果单项式xa+1y3与 12ybx2是同类项,那么 a,b 的值分别为( ) Aa2,b3 Ba1,b2 Ca2,b2 Da1,b3 6 (3 分)下列叙述,其中不正确的是( ) A两点确定一条直线 B同角(或等角)的余角相等 C过一点有且只有一条直线与已知直线平行 D两点之间的所有连线中,线段最短 7 (3 分)如图,线段 AB10cm,点 C 为线段 AB 上一点,BC3cm,点 D,E 分别为 AC 和 AB 的中点, 则线段 DE 的长为( ) A B1 C D2 8 (3 分)如图,将长方形纸条的一部分 ODCG 沿 OG 折叠到 O
3、D1C1G,若D1OG55,则AOD1等 于( ) A50 B55 C60 D70 9 (3 分)按如图所示的运算程序,能使输出的结果为 12 的是( ) Ax3,y3 Bx4,y2 Cx2,y4 Dx4,y2 10 (3 分)如图,把一块直角三角板的直角顶点放在直尺的一边上,若135,则2 等于( ) A35 B45 C55 D65 二、填空题(本大题共二、填空题(本大题共 4 个小题,每小题个小题,每小题 3 分,共分,共 12 分)分) 11 (3 分)x3y 的系数是 ,次数是 12 (3 分)在“手拉手活动”中,小明为捐助某贫困山区的一名同学,现已存款 300 元,他计划今后每月 存
4、款 20 元,n 月后存款总数是 元(用含 n 的代数式表示) 13 (3 分)已知2725,则 的补角为 14 (3 分)若“”是新规定的某种运算符号,设 abab+ab,则 2n8,则 n 三、解答题(本大题共三、解答题(本大题共 7 个题,共个题,共 58 分)分) 15 (10 分)计算下列各题: (1)13()+7|; (2)14+9()2+23 16 (12 分)解下列方程: (1)解方程:2(x2)83(4x1) ; (2)解方程:x2 17 (6 分)先化简,再求值:2(ab3a2)+5a2(3aba2),其中 a,b1 18 (6 分)如图是由一些棱长都为 1cm 的小正方体
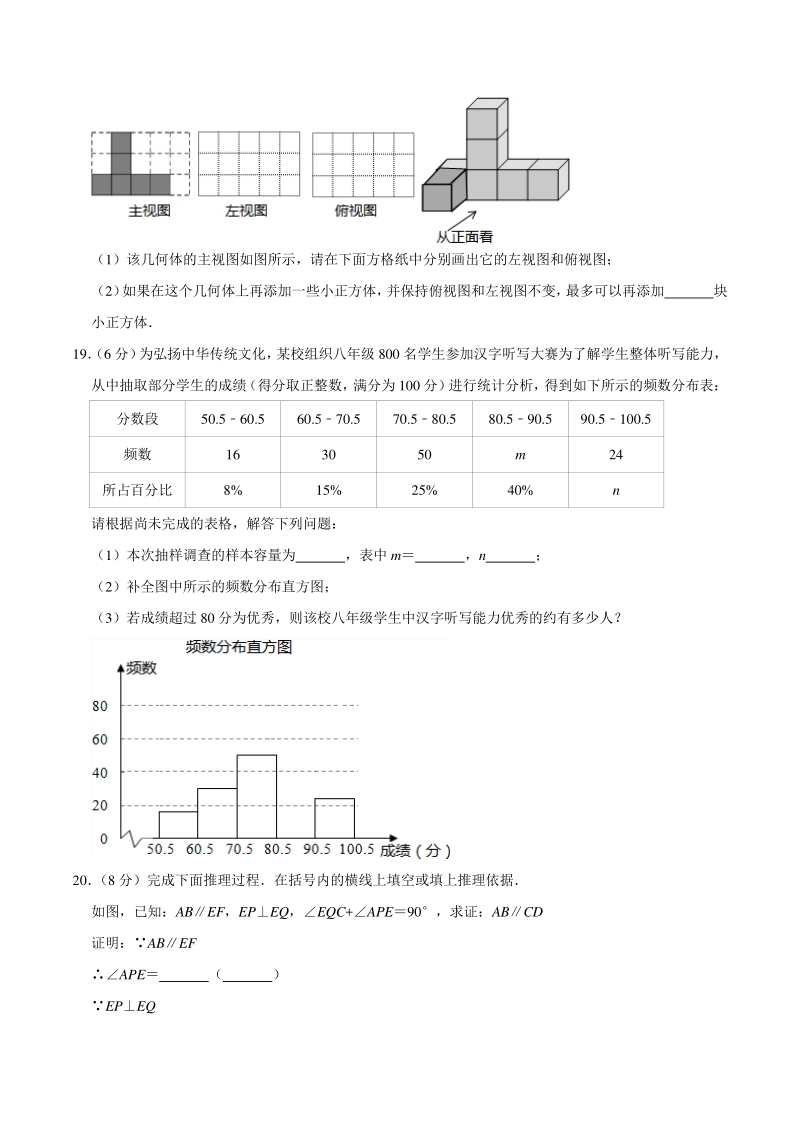
5、组合成的简单几何体 (1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图; (2) 如果在这个几何体上再添加一些小正方体, 并保持俯视图和左视图不变, 最多可以再添加 块 小正方体 19 (6 分) 为弘扬中华传统文化, 某校组织八年级 800 名学生参加汉字听写大赛为了解学生整体听写能力, 从中抽取部分学生的成绩 (得分取正整数, 满分为 100 分) 进行统计分析, 得到如下所示的频数分布表: 分数段 50.560.5 60.570.5 70.580.5 80.590.5 90.5100.5 频数 16 30 50 m 24 所占百分比 8% 15% 25% 40%
6、n 请根据尚未完成的表格,解答下列问题: (1)本次抽样调查的样本容量为 ,表中 m ,n ; (2)补全图中所示的频数分布直方图; (3)若成绩超过 80 分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人? 20 (8 分)完成下面推理过程在括号内的横线上填空或填上推理依据 如图,已知:ABEF,EPEQ,EQC+APE90,求证:ABCD 证明:ABEF APE ( ) EPEQ PEQ ( ) 即QEF+PEF90 APE+QEF90 EQC+APE90 EQC EF ( ) ABCD( ) 21 (10 分)某公司招聘外卖送餐员,送餐员的月工资由底薪 1000 元加上外卖送单补
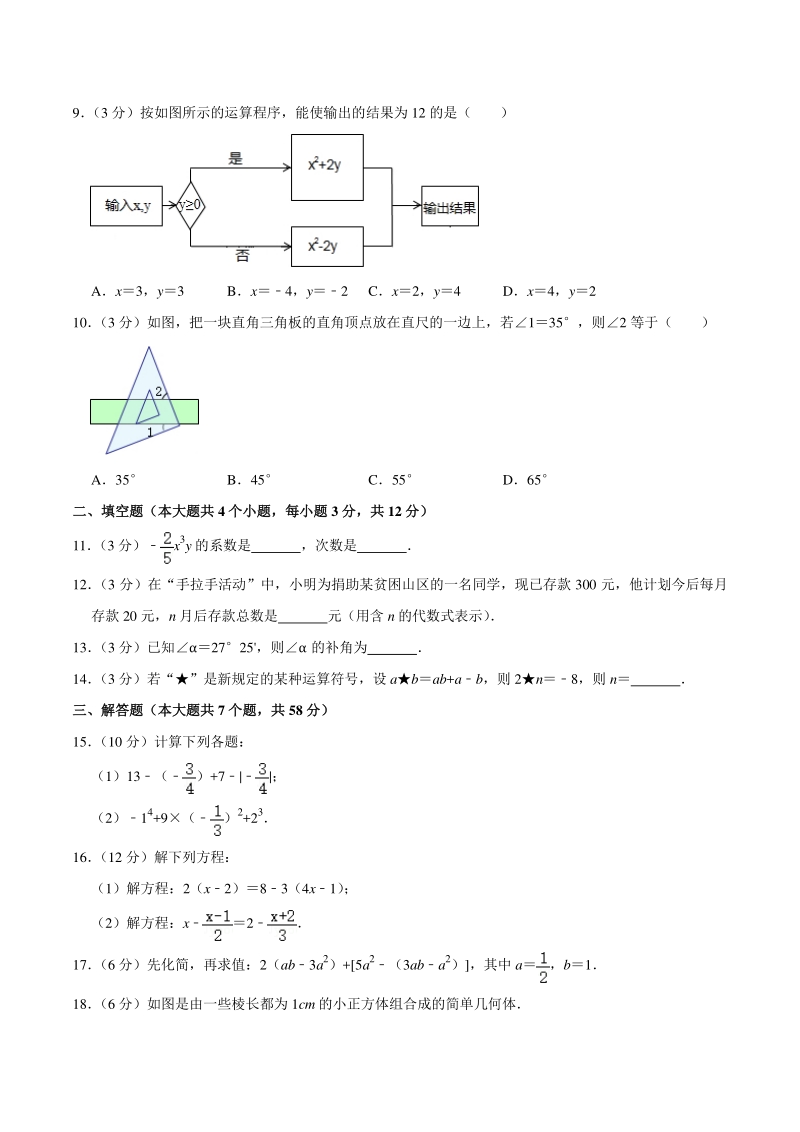
7、贴(送一次外卖称为 一单)构成,外卖送单补贴的具体方案如下: 外卖送单数量 补贴(元/单) 每月不超过 500 单 6 超过 500 单但不超过 m 单的部分(700m900) 8 超过 m 单的部分 10 (1)若某“外卖小哥”4 月份送餐 400 单,则他这个月的工资总额为多少元? (2)设 5 月份某“外卖小哥”送餐 x 单(x500) ,所得工资为 y 元,求 y 与 x 的函数关系式 (3)若某“外卖小哥”5 月份送餐 800 单,所得工资为 6500 元,求 m 的值 四、填空题(四、填空题(22-26 题,每题题,每题 3 分;分;27 题题 4 分,共分,共 19 分)分) 2
8、2 (3 分)若(m+1)x|m|30 是关于 x 的一元一次方程,则方程的解为 23 (3 分)若 x、y 为有理数,且(5x)2+|y+5|0,则()2021 24 (3 分)如图是一个正方体的展开图,Ax2,B2x2+1,C2x2,D2x+1,且相对两个面所表示的 整式的和都相等,则 E+F 25 (3 分)有理数 a,b,c 在数轴上的位置如图所示,化简|ca|+|cb|a+b| 26 (3 分)如图,有一根木棒 MN 放置在数轴上,它的两端 M、N 分别落在点 A、B 处将木棒在数轴上 水平移动,当 MN 的中点移动到点 B 时,点 N 所对应的数为 17.5,当 MN 的右三等分点
9、移动到点 A 时, 点 M 所对应的数为 4.5,则木棒 MN 的长度为 27 (4 分)我们可以用符号 f(a)表示代数式,当 a 为正数时,我们规定:如果 a 为偶数,f(a)0.5a, 如果 a 为奇数,f(a)5a+1例如 f(20)10,f (5)26设 a16,a2f(a1) ,a3f(a2) , 依此规律进行下去,得到一列数 a1、a2、a3、an(n 为正整数) ,则 a2019 ;计算 2a1a2+a3 a4+a5a6+a2017a2018+a2019a2020 五、解答题(共五、解答题(共 30 分)分) 28 (10 分) (1)若代数式(2x2+axy+6)(2bx23
10、x+5y1)的值与字母 x 的取值无关,试求 a22ab b2的值 (2)已知关于 x 方程 4x+2m3x+1 和方程 3x+2m6x+1 的解相同,试求(2m)2021(m)2020 的值 29 (10 分)今有三位好伙伴,小学就读于同一个班级初中的第一个寒假到了,某天就读于不同中学的他 们聚在一起,谈起数学,都兴奋不已,彼此抛出了一个数学问题 甲的问题是: (+)的值为多少? 乙的问题是:如图 1,将长方形纸片的一角折叠,使顶点 A 落在 F 处,折痕为 BC,作FBD 的角平分 线 BE,将FBD 沿 BF 折叠使 BE,BD 均落在FBC 的内部,且 BE 交 CF 于点 M,BD
11、交 CF 于 N若 BN 平分CBM,则ABC 的度数为多少? 丙的问题是: 如图 2, 线段 AB 表示一根对折的绳子, 点 P 在 AB 上且 APPB 若在 P 处将绳子剪断, 所得三段绳子的最大值为 8cm,则整条绳子剪断前的长度为多少? 如果用 a 表示甲的问题中的值;用 b 表示乙的问题中ABC 的度数,用 c 表示丙的问题中绳子长度的厘 米数 同学,你能超越他们,迅速算出 a、b、c 并将它们用“”连接起来吗?(要写求解过程) 30 (11 分)如果两个角的差的绝对值等于 60,就称这两个角互为“伙伴角” ,其中一个角叫做另一个角 的“伙伴角” (本题所有的角都指大于 0小于 1
12、80的角) ,例如180,220,|12| 60,则1 和2 互为“伙伴角” ,即1 是2 的“伙伴角” ,2 也是1 的“伙伴角” (1) 如图1, O为直线AB上一点, AOCEOD90, AOE60, 则AOE的 “伙伴角” 是 ; (2)如图 2,O 为直线 AB 上一点,AOC30,将BOC 绕着点 O 以每秒 1的速度逆时针旋转得 DOE,同时射线 OP 从射线 OA 的位置出发绕点 O 以每秒 4的速度逆时针旋转,当射线 OP 与射线 OB 重合时旋转同时停止,若设旋转时间为 t 秒,求当 t 为何值时,POD 与POE 互为“伙伴角” ; (3)如图 3,AOB160,射线 O
13、I 从 OA 的位置出发绕点 O 顺时针以每秒 6的速度旋转,旋转时 间为 t 秒(0t) ,射线 OM 平分AOI,射线 ON 平分BOI,射线 OP 平分MON,问:是否存 在 t 的值使得AOI 与POI 互为“伙伴角”?若存在,求出 t 的值;若不存在,请说明理由 参考答案与试题解析参考答案与试题解析 一、选择题(本大题共一、选择题(本大题共 10 个小题,每小题个小题,每小题 3 分,共分,共 30 分)分) 1 (3 分)8 的相反数是( ) A8 B C D8 【解答】解:由相反数的定义可知,8 的相反数是(8)8 故选:D 2 (3 分)将一个直角三角板绕直角边旋转一周,则旋转
14、后所得几何体是( ) A圆柱 B圆 C圆锥 D三角形 【解答】解:圆锥的轴截面是直角三角形,因而圆锥可以认为直角三角形以一条直角边所在的直线为轴 旋转一周得到 故直角三角形绕它的直角边旋转一周可形成圆锥 故选:C 3 (3 分)地球的半径约为 6400000 米,用科学记数法表示为( ) A6.4105 米 B640104 米 C6.4106 米 D64105 米 【解答】解:6400000 米,用科学记数法表示为 6.4106米, 故选:C 4 (3 分)下列式子,符合用字母表示数的书写格式的是( ) Aa3 B2x Ca3 D 【解答】解:A、原书写错误,正确的书写格式是,故此选项不符合题
15、意; B、原书写错误,正确的书写格式是x,故此选项不符合题意; C、原书写错误,正确的书写格式是 3a,故此选项不符合题意; D、原书写正确,故此选项符合题意 故选:D 5 (3 分)如果单项式xa+1y3与 12ybx2是同类项,那么 a,b 的值分别为( ) Aa2,b3 Ba1,b2 Ca2,b2 Da1,b3 【解答】解:根据题意得:a+12,b3, 则 a1 故选:D 6 (3 分)下列叙述,其中不正确的是( ) A两点确定一条直线 B同角(或等角)的余角相等 C过一点有且只有一条直线与已知直线平行 D两点之间的所有连线中,线段最短 【解答】解:A、两点确定一条直线,故 A 正确;
16、B、同角(或等角)的余角相等,故 B 正确; C、过直线外一点有且只有一条直线与已知直线平行,故 C 错误; D、两点之间的所有连线中,线段最短,故 D 正确; 故选:C 7 (3 分)如图,线段 AB10cm,点 C 为线段 AB 上一点,BC3cm,点 D,E 分别为 AC 和 AB 的中点, 则线段 DE 的长为( ) A B1 C D2 【解答】解:由线段的和差,得 ACABBC1037cm, 由点 D 是 AC 的中点, 所以 ADAC7cm; 由点 E 是 AB 的中点,得 AEAB105cm, 由线段的和差,得 DEAEAD5cm 故选:C 8 (3 分)如图,将长方形纸条的一部
17、分 ODCG 沿 OG 折叠到 OD1C1G,若D1OG55,则AOD1等 于( ) A50 B55 C60 D70 【解答】解:将长方形纸条的一部分 ODCG 沿 OG 折叠到 OD1C1G,D1OG55, D1OGDOG55, AOD1180555570, 故选:D 9 (3 分)按如图所示的运算程序,能使输出的结果为 12 的是( ) Ax3,y3 Bx4,y2 Cx2,y4 Dx4,y2 【解答】解:A、x3、y3 时,输出结果为 32+2315,不符合题意; B、x4、y2 时,输出结果为(4)22(2)20,不符合题意; C、x2、y4 时,输出结果为 22+2412,符合题意;
18、D、x4、y2 时,输出结果为 42+2220,不符合题意; 故选:C 10 (3 分)如图,把一块直角三角板的直角顶点放在直尺的一边上,若135,则2 等于( ) A35 B45 C55 D65 【解答】解:如图,1+390,135, 3901903555, 又直尺的两边平行, 23, 255 故选:C 二、填空题(本大题共二、填空题(本大题共 4 个小题,每小题个小题,每小题 3 分,共分,共 12 分)分) 11 (3 分)x3y 的系数是 ,次数是 4 【解答】解:单项式x3y 的系数是,次数是 4 故答案为:,4 12 (3 分)在“手拉手活动”中,小明为捐助某贫困山区的一名同学,现
19、已存款 300 元,他计划今后每月 存款 20 元,n 月后存款总数是 (300+20n) 元(用含 n 的代数式表示) 【解答】解:由题意可知,n 月后存款总数是(300+20n)元 故答案为: (300+20n) 13 (3 分)已知2725,则 的补角为 15235 【解答】解: 的补角180272517960272515235, 故答案为:15235 14 (3 分)若“”是新规定的某种运算符号,设 abab+ab,则 2n8,则 n 10 【解答】解:利用题中的新定义化简得:2n+2n8, 移项合并得:n10, 故答案为:10 三、解答题(本大题共三、解答题(本大题共 7 个题,共个

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2020 2021 学年 四川省 成都市 青羊区 石室 中学 年级 期末 数学试卷 答案 详解
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 数学试卷
- 成都市石室联合中学
- 2020-2021成都市七上
- 2020-2021成都市七上数学
- 2020-2021成都市九上期末数学
- 2021年四川省成都市青羊区年级下期末数学试卷
- 2021年四川省成都市青羊区五年级下期末 语文
- 2021年四川省成都市青羊区七年级下期末数学试卷含答案解析
- 四川省成都青羊区2021年七年级下期末语文试卷含答案
- 2021年四川省成都市青羊区五年级下期末数学试卷含答案解析
- 四川省成都青羊区2020年七年级下期末语文试卷含答案
- 四川省成都市七年级上期中数学试卷
- 四川省成都市七年级上期试卷
- 四川省成都市七年级上期期末试卷
- 梅岭中学七年级上期末数学试卷
- 扬州 梅岭中学七年级上期末数学试卷
- 2021-2022学年四川省成都市高新区七年级上期末数学试卷
- 四川省成都青羊区 七年级 期末
- 2021年湖南省成都市青羊区七年级下期末数学试卷含答案解析
- 四川省成都市石室联合中学



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-178495.html