2021年天津市和平区中考数学结课质检试卷（含答案解析）

《2021年天津市和平区中考数学结课质检试卷（含答案解析）》由会员分享，可在线阅读，更多相关《2021年天津市和平区中考数学结课质检试卷（含答案解析）（23页珍藏版）》请在七七文库上搜索。

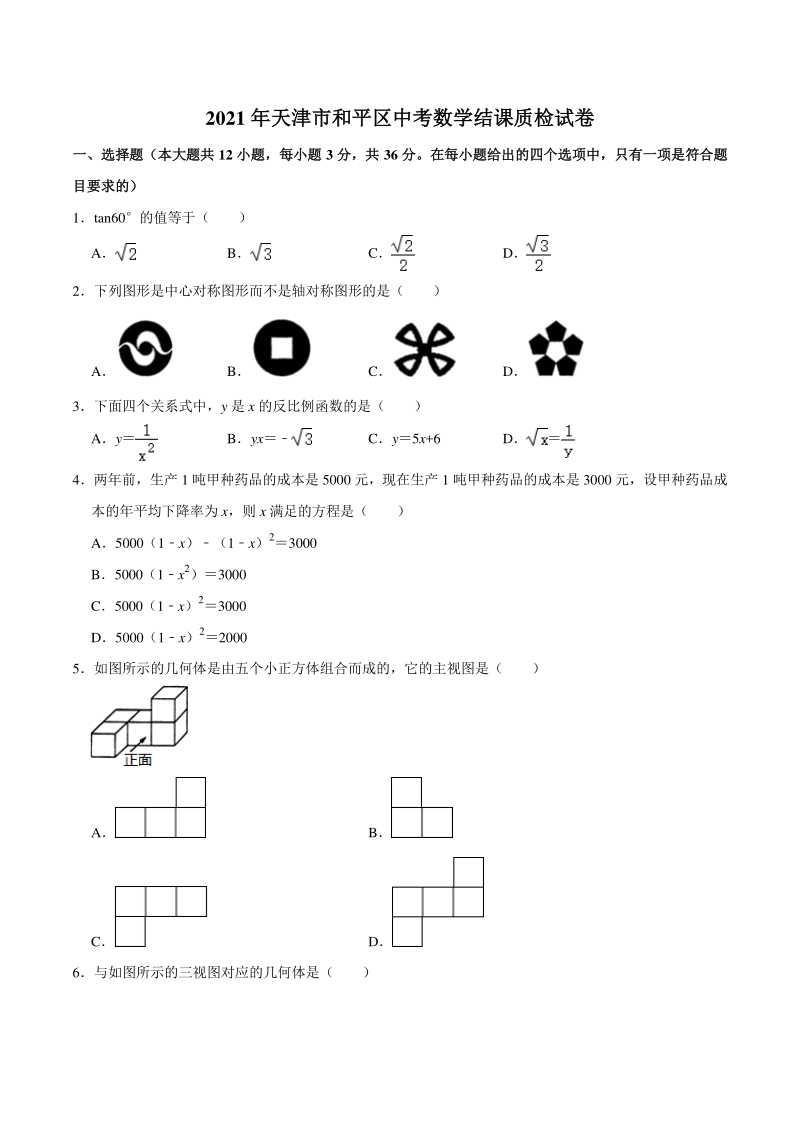
1、2021 年天津市和平区中考数学结课质检试卷年天津市和平区中考数学结课质检试卷 一、选择题（本大题共一、选择题（本大题共 12 小题，每小题小题，每小题 3 分，共分，共 36 分。在每小题给出的四个选项中，只有一项是符合题分。在每小题给出的四个选项中，只有一项是符合题 目要求的）目要求的） 1tan60的值等于（ ） A B C D 2下列图形是中心对称图形而不是轴对称图形的是（ ） A B C D 3下面四个关系式中，y 是 x 的反比例函数的是（ ） Ay Byx Cy5x+6 D 4两年前，生产 1 吨甲种药品的成本是 5000 元，现在生产 1 吨甲种药品的成本是 3000 元，设甲

2、种药品成 本的年平均下降率为 x，则 x 满足的方程是（ ） A5000（1x）（1x）23000 B5000（1x2）3000 C5000（1x）23000 D5000（1x）22000 5如图所示的几何体是由五个小正方体组合而成的，它的主视图是（ ） A B C D 6与如图所示的三视图对应的几何体是（ ） A B C D 7两地的实际距离是 2000m，在地图上量得这两地的距离为 2cm，这幅地图的比例尺是（ ） A1：1000000 B1：100000 C1：2000 D1：1000 8如图，点 P 是反比例函数 y（k0）的图象上任意一点，过点 P 作 PMx 轴，垂足为 M若POM

3、 的面积等于 2，则 k 的值等于（ ） A4 B4 C2 D2 9如图，矩形 ABCD 绕点 A 逆时针旋转 （090）得到矩形 ABCD，此时点 B恰好在 DC 边 上，若BBC15，则 的大小为（ ） A15 B25 C30 D45 10半径相等的圆的内接正三角形、正方形、正六边形的边长之比为（ ） A1： B：1 C3：2：1 D1：2：3 11如图，AB 是O 的直径，ABAC，BAC45，O 交 BC 于点 D，交 AC 于点 E，DF 与O 相切 于点 D，交 AC 于点 F，OD 与 BE 相交于点 H下列结论错误的是（ ） ABDCD BBHDF C2 DBC2CE 12yx

4、2+（1a）x+1 是关于 x 的二次函数，当 x 的取值范围是 1x3 时，y 在 x1 时取得最大值，则 实数 a 的取值范围是（ ） Aa5 Ba5 Ca3 Da3 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 13 有一个质地均匀的正十二面体，十二个面上分别写有 112 这十二个整数， 投掷这个正十二面体一次， 则向上一面的数字是 2 的概率是 14在一个不透明的袋子中装有 4 个除颜色外完全相同的小球，其中白球 1 个，黄球 1 个，红球 2 个，摸 出一个球不放回，再摸出一个球，两次都摸到红球的概率是 15如图，在ABC

5、中，点 D，E 分别是边 AB，AC 的中点，高 AH 交 DE 于点 F，若 AH2，则 AF 的长 为 16已知一次函数 ykx+2（k 是常数，k0） ，y 随 x 的增大而减小，写出一个符合条件的 k 的值为 17如图，AB 是O 的直径，C 为O 上一点，以点 A 为旋转中心，把ABC 顺时针旋转得ADE记旋 转角为 ，ABC 为 ，当旋转后满足 BDCA 时， （用含 的式子表示） 18系统找不到该试题 三、解答题（本大题共三、解答题（本大题共 7 小题，共小题，共 66 分，解答应写出文字说明、演算步骤或推理过程）分，解答应写出文字说明、演算步骤或推理过程） 19 （8 分）解方

6、程：x（2x5）4x10 20 （8 分）已知抛物线 yax2+bx+c（a0）与 y 轴的交点为 C若自变量 x 和函数值 y 的部分对应值如表 所示： x 1 0 1 y 10 5 4 （）求点 C 的坐标； （）求 y 与 x 之间的函数关系式 21 （10 分）已知 AB 是O 的直径，CD 切O 于点 C，交 AB 的延长线于点 D，且D30，连接 AC （）如图，求A 的大小； （ ） 如 图 ， E是 O上 一 点 ， BCE 120 ， BE 8 ， 求CE的 长 22 （10 分）已知某航空母舰舰长 BD 为 306m，航母前端点 E 到水平甲板 BD 的距离 DE 为 6m

7、，舰岛顶端 A 到 BD 的距离是 AC，经测量，BAC71.6，EAC80.6，请计算舰岛 AC 的高度（结果精确到 1m） （参考数据： sin71.60.95， cos71.60.32， tan71.63.01， sin80.60.99， cos80.60.16， tan80.66.04） 23 （10 分）已知小明家与学校在一条笔直的公路旁，学校离小明家 2200m一天，小明从家出发去上学， 匀速走了 400m 时看到路旁有一辆共享单车，此时用了 5min、小明用 1min 开锁后骑行 6min 到达学校， 给出的图象反映了这个过程中小明离家的距离 ym 与离开家的时间 xmin 之间

8、的对应关系 请根据相关信息，解答下列问题： （）填表： 离开小明家的时 间/min 2 4 5 6 离小明家的距离 /m 160 400 （）填空：小明骑车的速度为 m/min； 当小明离家的距离为 1900m 时，他离开家的时间为 min； （）当 0 x12 时，直接写出 y 关于 x 的函数解析式 24 （10 分）在平面直角坐标系中，有正方形 OBCD 和正方形 OEFG，E（2，0） ，B（0， 2） （）如图，求 BE 的长； （）将正方形 OBCD 绕点 O 逆时针旋转，得正方形 OBCD 如图，当点 B恰好落在线段 DG 上时，求 BE 的长； 将正方形 OBCD绕点 O 继续

9、逆时针旋转，线段 DG 与线段 BE 的交点为 H，求GHE 与BHD面 积之和的最大值，并求出此时点 H 的坐标（直接写出结果） 25 （10 分）已知抛物线 C1：yx2+kx2k（k 是常数） ，顶点为 N （）若抛物线 C1经过点（3，7） ， 求抛物线 C1的解析式及顶点坐标； 若将抛物线 C1向上平移 8 个单位长度， 再向左平移 2 个单位长度， 得抛物线 C2 点 A 的横坐标为3， 且点 A 在抛物线 C2上，若抛物线 C2与 y 轴交于点 B，连接 AB，C 为抛物线 C2上一点，且位于线段 AB 的上方，过点 C 作 CDx 轴于点 D，CP 交 AB 于点 E，若 CE

10、ED，求点 C 的坐标； （）已知点 M（2，0） ，且无论 k 取何值，抛物线 C1都经过定点 H，当MHN60时，求抛 物线 C1的解析式 2021 年天津市和平区中考数学结课质检试卷年天津市和平区中考数学结课质检试卷 参考答案与试题解析参考答案与试题解析 一、选择题（本大题共一、选择题（本大题共 12 小题，每小题小题，每小题 3 分，共分，共 36 分。在每小题给出的四个选项中，只有一项是符合题分。在每小题给出的四个选项中，只有一项是符合题 目要求的）目要求的） 1tan60的值等于（ ） A B C D 【分析】根据特殊角的三角函数值，可得答案 【解答】解：tan60， 故选：B 2

11、下列图形是中心对称图形而不是轴对称图形的是（ ） A B C D 【分析】根据轴对称图形与中心对称图形的概念求解 【解答】解：A、是中心对称图形，不是轴对称图形；故 A 正确； B、是中心对称图形，也是轴对称图形；故 B 错误； C、是中心对称图形，也是轴对称图形；故 C 错误； D、不是中心对称图形，是轴对称图形；故 D 错误； 故选：A 3下面四个关系式中，y 是 x 的反比例函数的是（ ） Ay Byx Cy5x+6 D 【分析】直接利用反比例函数的定义分析得出答案 【解答】解：A、y，是 y 与 x2成反比例函数关系，故此选项错误； B、yx，y 是 x 的反比例函数，故此选项正确；

12、C、y5x+6 是一次函数关系，故此选项错误； D、，不符合反比例函数关系，故此选项错误 故选：B 4两年前，生产 1 吨甲种药品的成本是 5000 元，现在生产 1 吨甲种药品的成本是 3000 元，设甲种药品成 本的年平均下降率为 x，则 x 满足的方程是（ ） A5000（1x）（1x）23000 B5000（1x2）3000 C5000（1x）23000 D5000（1x）22000 【分析】由两年前及现在生产 1 吨甲种药品的成本，即可得出关于 x 的一元二次方程，此题得解 【解答】解：依题意，得：5000（1x）23000 故选：C 5如图所示的几何体是由五个小正方体组合而成的，它

13、的主视图是（ ） A B C D 【分析】从正面看得到从左往右 3 列正方形的个数依次为 1，1，2，依此判断即可 【解答】解：从正面看得到从左往右 3 列正方形的个数依次为 1，1，2， 故选：A 6与如图所示的三视图对应的几何体是（ ） A B C D 【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形 【解答】解：从正视图可以排除 C，故 C 选项错误； 从左视图可以排除 A，故 A 选项错误； 从左视图可以排除 D，故 D 选项错误； 符合条件的只有 B 故选：B 7两地的实际距离是 2000m，在地图上量得这两地的距离为 2cm，这幅地图的比例尺是（ ） A1

14、：1000000 B1：100000 C1：2000 D1：1000 【分析】先把 2000m 化为 200000cm，然后根据比例尺的定义求解 【解答】解：2000m200000cm， 所以这幅地图的比例尺为 2：2000001：100000 故选：B 8如图，点 P 是反比例函数 y（k0）的图象上任意一点，过点 P 作 PMx 轴，垂足为 M若POM 的面积等于 2，则 k 的值等于（ ） A4 B4 C2 D2 【分析】利用反比例函数 k 的几何意义得到|k|2，然后根据反比例函数的性质和绝对值的意义确定 k 的值 【解答】解：POM 的面积等于 2， |k|2， 而 k0， k4 故

15、选：A 9如图，矩形 ABCD 绕点 A 逆时针旋转 （090）得到矩形 ABCD，此时点 B恰好在 DC 边 上，若BBC15，则 的大小为（ ） A15 B25 C30 D45 【分析】连接 BB，求出ABB75，再利用等腰三角形的性质，可得结论 【解答】解：连接 BB 四边形 ABCD 是矩形， ABC90， CBB15， ABB901575， ABAB， ABBABB75， ABB18027530， 30， 故选：C 10半径相等的圆的内接正三角形、正方形、正六边形的边长之比为（ ） A1： B：1 C3：2：1 D1：2：3 【分析】从中心向边作垂线，构建直角三角形，通过解直角三角形

16、可得 【解答】解：设圆的半径是 r， 则多边形的半径是 r， 则内接正三角形的边长是 2rsin60r， 内接正方形的边长是 2rsin45r， 正六边形的边长是 r， 因而半径相等的圆的内接正三角形、正方形、正六边形的边长之比为：1 故选：B 11如图，AB 是O 的直径，ABAC，BAC45，O 交 BC 于点 D，交 AC 于点 E，DF 与O 相切 于点 D，交 AC 于点 F，OD 与 BE 相交于点 H下列结论错误的是（ ） ABDCD BBHDF C2 DBC2CE 【分析】证明 ODAC，利用三角形中位线性质可对 A 选项进行判断；再证明 ODBE，利用垂径定理 得到 BHEH

17、，根据切线的性质得 ODDF，易得四边形 DHEF 为矩形，所以 DFHE，于是可对 B 选 项进行判断；证明 AEBE，则，根据垂径定理得到，所以2，则可对 C 选项进 行判断；连接 DE，如图，计算出ABCACB67.5，则根据圆内接四边形的性质得到EDC A45，DECABC67.5，所以 CDCE，则 BC2CE，则可对 D 选项进行判断 【解答】解：ABAC， ABCACB， OBOD， OBDODB， ODBACB， ODAC， 而 OAOB， BDCD，所以 A 选项的结论正确； AB 为直径， AEB90， ODAC， ODBE， BHEH， DF 为切线， ODDF， 四边形

18、 DHEF 为矩形， DFHE， BHDF，所以 B 选项的结论正确； A45，AEB90， AEBE， ， ODBE， ， 2，所以 C 选项的结论正确； 连接 DE，如图， ABCACB（180A）（180A）（18045）67.5， EDCA45，DECABC67.5， CDCE， 2CD2CE， 即 BC2CE，所以 D 选项的结论错误 故选：D 12yx2+（1a）x+1 是关于 x 的二次函数，当 x 的取值范围是 1x3 时，y 在 x1 时取得最大值，则 实数 a 的取值范围是（ ） Aa5 Ba5 Ca3 Da3 【分析】由于二次函数的顶点坐标不能确定，故应分对称轴不在 1x

19、3 和对称轴在 1x3 内两种情 况进行解答 【解答】解：第一种情况： 当二次函数的对称轴不在 1x3 范围内时，此时，对称轴一定在 x3 的右边，函数方能在这个区域取 得最大值， x3，即 a7， 第二种情况： 当对称轴在 1x3 范围内时， 对称轴一定是在 x （1+3）2 的右边，因为如果在中点的左边的话， 就是在 x3 的地方取得最大值，即： x，即 a5（此处若 a 取 5 的话，函数就在 1 和 3 的地方都取得最大值） 综合上所述 a5 故选：B 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 13 有一个质地均匀的正十二

20、面体，十二个面上分别写有 112 这十二个整数， 投掷这个正十二面体一次， 则向上一面的数字是 2 的概率是 【分析】根据概率的求法，找准两点：全部情况的总数；符合条件的情况数目；二者的比值就是其 发生的概率 【解答】解：共 12 个面，分别写有 112 这十二个整数， 投掷这个正十二面体一次，则向上一面的数字是 2 的概率是， 故答案为： 14在一个不透明的袋子中装有 4 个除颜色外完全相同的小球，其中白球 1 个，黄球 1 个，红球 2 个，摸 出一个球不放回，再摸出一个球，两次都摸到红球的概率是 【分析】列举出所有情况，看两次都摸到红球的情况占总情况的多少即可 【解答】解： 一共有 12

21、 种情况，有 2 种情况两次都摸到红球， 两次都摸到红球的概率是 故答案为 15如图，在ABC 中，点 D，E 分别是边 AB，AC 的中点，高 AH 交 DE 于点 F，若 AH2，则 AF 的长 为 1 【分析】根据三角形中位线得出 AFAH，解答即可 【解答】解：在ABC 中，点 D，E 分别是边 AB，AC 的中点， DE 是ABC 的中位线， 高 AH 交 DE 于点 F，AH2， AFAH1， 故答案为：1 16已知一次函数 ykx+2（k 是常数，k0） ，y 随 x 的增大而减小，写出一个符合条件的 k 的值为 1 【分析】根据一次函数的性质，y 随 x 的增大而减小 k0，不

22、妨令 k1 即可 【解答】解：一次函数 y 随 x 的增大而减小， k0， 不妨设 k1， 故答案为：1 17如图，AB 是O 的直径，C 为O 上一点，以点 A 为旋转中心，把ABC 顺时针旋转得ADE记旋 转角为 ，ABC 为 ，当旋转后满足 BDCA 时， 2 （用含 的式子表示） 【分析】 由旋转的性质可得ABCADE， BAD， 再利用等腰三角形的性质表示出BAD （180 ） ，利用平行线的性质可得答案 【解答】解：把ABC 顺时针旋转得AED， ABCADE，BAD， ABAC， ABDADB， 在ABC 中，BAD（180） ， AB 是O 的直径， BCA90， BDCA，

23、CBD90， 90（180） ， 整理得，2 故答案为：2 18系统找不到该试题 三、解答题（本大题共三、解答题（本大题共 7 小题，共小题，共 66 分，解答应写出文字说明、演算步骤或推理过程）分，解答应写出文字说明、演算步骤或推理过程） 19 （8 分）解方程：x（2x5）4x10 【分析】由于方程左右两边都含有（2x5） ，可将（2x5）看作一个整体，然后移项，再分解因式求解 【解答】解：原方程可变形为： x（2x5）2（2x5）0， （2x5） （x2）0， 2x50 或 x20； 解得 x1，x22 20 （8 分）已知抛物线 yax2+bx+c（a0）与 y 轴的交点为 C若自变量

24、 x 和函数值 y 的部分对应值如表 所示： x 1 0 1 y 10 5 4 （）求点 C 的坐标； （）求 y 与 x 之间的函数关系式 【分析】 （）由表格数据可知抛物线 yax2+bx+c 经过点（0，5） ，即可求得 C 为（0，5） ； （）根据待定系数法即可求得 y 与 x 之间的函数关系式 【解答】解： （I）由抛物线 yax2+bx+c 经过点（0，5） ， C（0，5） ； （）由已知得 c5， yax2+bx+5， 点（1，10） ， （1，4）在抛物线 yax2+bx+5 上， ，解得， y 与 x 之间的函数关系式为 y2x23x+5 21 （10 分）已知 AB 是

25、O 的直径，CD 切O 于点 C，交 AB 的延长线于点 D，且D30，连接 AC （）如图，求A 的大小； （ ） 如 图 ， E是 O上 一 点 ， BCE 120 ， BE 8 ， 求CE的 长 【分析】 （）连接 OC，先由切线的性质得OCD90，再由直角三角形的性质得COB60，然 后由圆周角定理即可求解； （）连接 OC 交 BE 于点 F，先证BOC 是等边三角形，得OCB60，再证CFE90，则 OC BE，然后由垂径定理得 EFBE4，即可解决问题 【解答】解： （）连接 OC，如图： CD 切O 于点 C， CDOC， OCD90， D30， COB90D60， ACOB3

26、0； （）连接 OC 交 BE 于点 F，如图： 由（1）得：COB60， OBOC， BOC 是等边三角形， OCB60， BCE120， ECFBCEOCB1206060， EA30， CFE180ECFE180603090， OCBE， EFBE84， cosE， CE 22 （10 分）已知某航空母舰舰长 BD 为 306m，航母前端点 E 到水平甲板 BD 的距离 DE 为 6m，舰岛顶端 A 到 BD 的距离是 AC，经测量，BAC71.6，EAC80.6，请计算舰岛 AC 的高度（结果精确到 1m） （参考数据： sin71.60.95， cos71.60.32， tan71.6

27、3.01， sin80.60.99， cos80.60.16， tan80.66.04） 【分析】设 ACxm作 EHAC 于 H，则四边形 EHCD 是矩形根据 BD306，构建方程即可解决问 题 【解答】解：设 ACxm作 EHAC 于 H，则四边形 EHCD 是矩形 由题意，DECH6m，CDEHAHtan80.66.04（x6） ，BCACtan71.63.01x， BD306m， 3.01x+6.04（x6）306， 解得：x38， 答：岛 AC 的高度为 38 米 23 （10 分）已知小明家与学校在一条笔直的公路旁，学校离小明家 2200m一天，小明从家出发去上学， 匀速走了 4

28、00m 时看到路旁有一辆共享单车，此时用了 5min、小明用 1min 开锁后骑行 6min 到达学校， 给出的图象反映了这个过程中小明离家的距离 ym 与离开家的时间 xmin 之间的对应关系 请根据相关信息，解答下列问题： （）填表： 离开小明家的时 间/min 2 4 5 6 离小明家的距离 /m 160 320 400 400 （）填空：小明骑车的速度为 300 m/min； 当小明离家的距离为 1900m 时，他离开家的时间为 11 min； （）当 0 x12 时，直接写出 y 关于 x 的函数解析式 【分析】 （）根据函数图象横、纵坐标表示的意义填空即可； （）根据“速度路程时间

29、”计算即可； （）根据分段函数，利用待定系数法求解即可 【解答】解： （）当 x4 时，y40054320； 当 x6 时，y400； 故答案为：320；400； （）小明骑车的速度为： （2200400）（126）300（m/min） ； 当小明离家的距离为 1900m 时，他离开家的时间为：6+（1900400）30011（min） ， 故答案为：300；11； （）当 0 x5 时，y80 x； 当 5x6 时，y400； 当 6x12 时，设 y 关于 x 的函数解析式为 ykx+b，根据题意，得： ，解得， y300 x1400 24 （10 分）在平面直角坐标系中，有正方形 OBC

30、D 和正方形 OEFG，E（2，0） ，B（0， 2） （）如图，求 BE 的长； （）将正方形 OBCD 绕点 O 逆时针旋转，得正方形 OBCD 如图，当点 B恰好落在线段 DG 上时，求 BE 的长； 将正方形 OBCD绕点 O 继续逆时针旋转，线段 DG 与线段 BE 的交点为 H，求GHE 与BHD面 积之和的最大值，并求出此时点 H 的坐标（直接写出结果） 【分析】 （）由勾股定理可求出答案； （）证明ODGOBE（SAS） ，由全等三角形的性质得出 DGBE，连接 OC交 DG 于点 M， 由勾股定理和锐角三角函数求出 DM 和 GM 的长，则可求出答案； 对于EGH， 点 H

31、在以 EG 为直径的圆上， 即当点 H 与点 O 重合时， EGH 的高最大； 对于BDH， 点 H 在以 BD为直径的圆上，即当点 H 与点 O 重合时，BDH 的高最大，即可确定出面积的最大值 【解答】解： （）E（2，0） ，B（0，2） ， OE2，OB2， BE2； （）四边形 OBCD和四边形 OEFG 都为正方形， ODOB，DOBGOE90，OGOE， DOB+BOGGOE+BOG， 即DOGBOE， 在ODG 和OBE 中， ， ODGOBE（SAS） ， DGBE， 连接 OC交 DG 于点 M， 四边形 OBCD是正方形， OMGODC90，MDO45， 在 RtOMD中

32、，cosMDO， DMODcos45OBcos452， 在 RtOMG 中，根据勾股定理得：GM， DGDM+GM+， BEDG+； GHE 和BHD面积之和的最大值为 6，理由为： 对于EGH，点 H 在以 EG 为直径的圆上， 当点 H 与点 O 重合时，EGH 的高最大； 对于BDH，点 H 在以 BD为直径的圆上， 当点 H 与点 O 重合时，BDH 的高最大， 则GHE 和BHD面积之和的最大值为 2+46，此时 H（0，0） 25 （10 分）已知抛物线 C1：yx2+kx2k（k 是常数） ，顶点为 N （）若抛物线 C1经过点（3，7） ， 求抛物线 C1的解析式及顶点坐标；

33、若将抛物线 C1向上平移 8 个单位长度， 再向左平移 2 个单位长度， 得抛物线 C2 点 A 的横坐标为3， 且点 A 在抛物线 C2上，若抛物线 C2与 y 轴交于点 B，连接 AB，C 为抛物线 C2上一点，且位于线段 AB 的上方，过点 C 作 CDx 轴于点 D，CP 交 AB 于点 E，若 CEED，求点 C 的坐标； （）已知点 M（2，0） ，且无论 k 取何值，抛物线 C1都经过定点 H，当MHN60时，求抛 物线 C1的解析式 【分析】 （）将（3，7）代入 yx2+kx2k，即可求解； 由平移的性质得出抛物线 C2：y（x+1）2+5，求出直线 AB 的解析式为 yx+

34、4，设 C（t，t2 2t+4） ，得出 E（t，t+2） ，由点 E 在直线 AB 上可得出答案； （）分三种情况，若2 时，若2 时，若2 时，由直角三角形的性质可求出答案 【解答】解： （）抛物线 C1经过点（3，7） ， 79+3k2k， 得 k2， 故抛物线 C1的表达式为 yx2+2x4， yx2+2x4（x1）23， 抛物线的顶点坐标为（1，3） ； 如图， 把 y （x1） 23 向上平移 8 个单位， 再向左平移 2 个单位长度， 得抛物线 C2： y （x+1） 2+5， 即 yx22x+4， 当 x3 时，y（3）22（3）+41， A（3，1） ， 当 x0 时，y4，

35、 B（0，4） ， 设直线 AB 的解析式为 ykx+b， ， ， 直线 AB 的解析式为 yx+4， 设 C（t，t22t+4） ， 点 C 位于线段 AB 的上方，且 CEED， E（t，t+2） ， E 点在直线 AB 上， t+2t+4， 解得 t1t22， C（2，4） （）由 yx2+kx2kk（x2）x2， 当 x20 时，x2，y4， 无论 k 取何值时，抛物线 C1都经过定点 H（2，4） yx2+kx2k2k， 抛物线 C1的顶点坐标为 N（，2k） 若2 时，则 k4， 如图 2，过点 H 作 HIx 轴于点 I，分别过点 H，N 作 y 轴，x 轴的垂线交于点 G， M（2，0） ，H（2，4） ， MI，HI4， tanMHI， MHI30， MHN60， NHI30， NHG60， 由 tanNHG， 解得 k4+2或 k4（不合题意，舍去） ， k4+2 若2 时，则 k4， 如图 3，过点 H 作 HIx 轴于点 I，分别过点 H，N 作 y 轴，x 轴的垂线交于点 G， 同理可得MHI30， MHN60， NHHI， 即2k4， 解得 k4（不合题意，舍去） 若2，则 N，H 重合，不合题意，舍去 综合以上可得，抛物线 C1的解析式为