1、2021 年年中考中考数学二轮复习探索规律数学二轮复习探索规律-图形变化规律专题突破训练图形变化规律专题突破训练 1蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的 截面图其中第一个图有 1 个蜂巢，第二个图有 7 个蜂巢，第三个图有 19 个蜂巢，按此规律，第 5 个 图的蜂巢总数的个数是（ ） A61 B62 C63 D65 2把圆形按如图所示的规律拼图案，其中第个图案中有 1 个圆形，第个图案中有 5 个圆形，第个 图案有 11 个圆形，第个图案有 19 个圆形，按此规律排列下去，第 7 个图案中圆形的个数为（ ） A42 B54 C55 D56
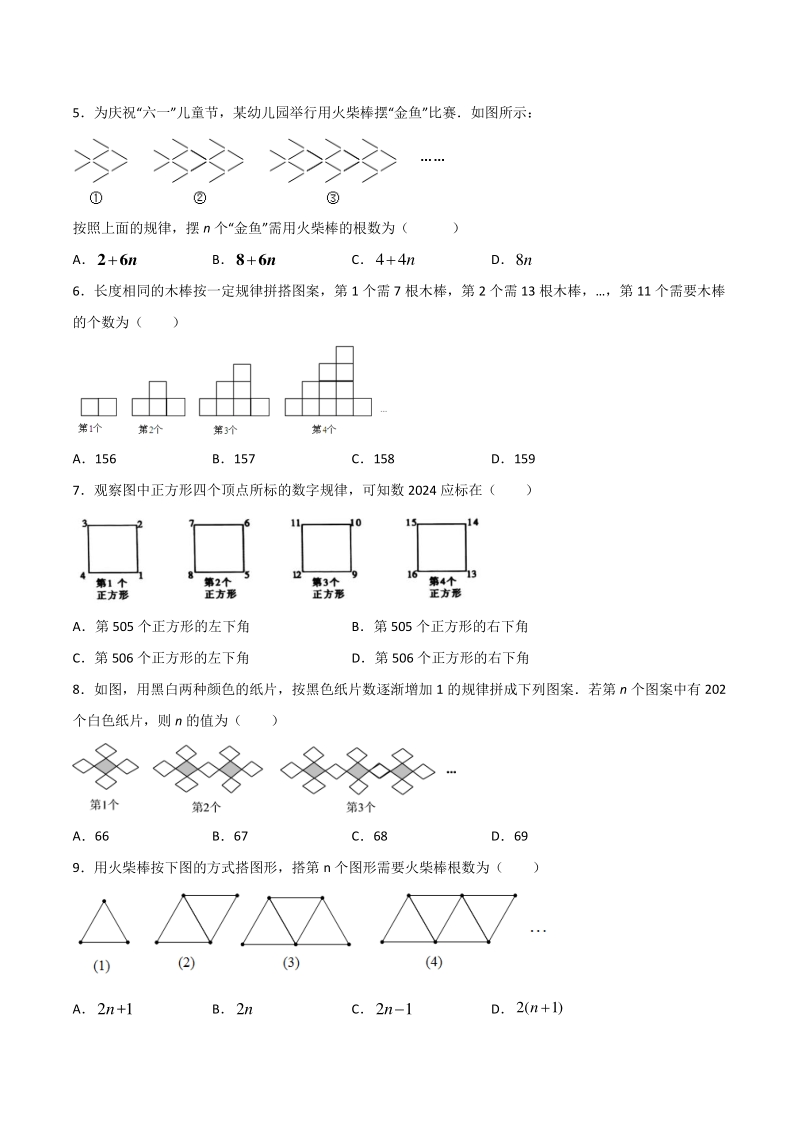
2、 3如图，是一个三角形，分别连接这个三角形三边中点得到图，再连接图中间小三角形三边的中 点得到图，按这样的方法进行下去，第 n 个图形中共有三角形的个数为（ ） A2n3 B4n1 C4n3 D4n2 4人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，如图中的每一个小正方形表示一块 地砖，如果按图 1、图 2、图 3的次序铺设地砖，把第 n 个图形用图 n 表示，那么图 2021 中的白色小正方 形地砖的块数比黑色小正方形地砖的块数多（ ） A8089 B8084 C6063 D14147 5为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛如图所示： 按照上面的规律，摆 n
3、 个“金鱼”需用火柴棒的根数为（ ） A2 6n B8 6n C44n D8n 6长度相同的木棒按一定规律拼搭图案，第 1 个需 7 根木棒，第 2 个需 13 根木棒，第 11 个需要木棒 的个数为（ ） A156 B157 C158 D159 7观察图中正方形四个顶点所标的数字规律，可知数 2024 应标在（ ） A第 505 个正方形的左下角 B第 505 个正方形的右下角 C第 506 个正方形的左下角 D第 506 个正方形的右下角 8如图，用黑白两种颜色的纸片，按黑色纸片数逐渐增加 1 的规律拼成下列图案若第 n 个图案中有 202 个白色纸片，则 n 的值为（ ） A66 B67
4、 C68 D69 9用火柴棒按下图的方式搭图形，搭第 n 个图形需要火柴棒根数为（ ） A21n+ B2n C21n D2( 1)n 10如图所示图形是由相同的小五角星按一定的规律排列组合而成，其中第一个图形有 6 个五角星，第二 个图形有 10 个五角星，第三个图形有 16 个五角星，第四个图形有 24 个五角星，则第八个图形五角 星的个数为（ ） A74 B76 C78 D80 11如图，都是由棱长为1的正方体叠成的图形例如：第个图形由1个正方体叠成，第个图形由4个 正方体叠成， 第个图形由10个正方体叠成， 低此规律， 第10个图形由n个正方体叠成， 则n的值为 （ ） A220 B16
5、5 C120 D55 12如图，正三角形ABC的边长为1，将线段AC绕点A逆时针旋转120至 1 AP，形成第一个扇形；将线 段 1 BP绕点B逆时针旋转120至 2 BP，形成第二个扇形；将线段 2 CP绕点C逆时针旋转120至 3 CP，形成 第三个扇形；将线段 3 AP绕点A逆时针旋转120至 4 AP，形成第四个扇设l为第n个扇形的弧 （1,2,3n ） ，则 2021 l_ 13如图，在平面直角坐标系中，一电子蚂蚁按照设定程序从原点 O 出发，按图中箭头所示的方向运动， 第 1 次从原点运动到点1,2，第 2 次接着运动到点2,0，第 3 次接着运动到点2, 2，第 4 次接着运动
6、到点4, 2，第 5 次接着运动到点4,0，第 6 次接着运动到点5,2按这样的运动规律，经过 2019 次运动后，电子蚂蚁运动到的位置的坐标是_ 14如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、 向右的方向依次不断移动， 每次移动 1 个单位， 其移动路线如图所示， 第 1 次移动到 1 A， 第 2 次移动到 2 A， 第 3 次移动到 3 A，第n次移动到 n A，则 22020 OA A的面积是_ 15如图，已知MON=30，点 123 ,A A A.在射线 ON 上，点 123 ,B B B.在射线 OM 上， 112233334 ,AB
7、 AA B AA B A.均为等边三角形，若 1 1OA ，则 202020202021 ABA的边长为_ 16观察下列图中所示的一系列“”图形，它们是按一定规律排列的，依照此规律，第 2021 个图形中共有 _个 17用火柴按如图的方式搭六边形组成的图形，如图搭 1 个六边形的图形需要 6 根火柴；如图搭 2 个六边形的图形需要 11 根火柴，如图搭 3 个六边形的图形需要 16 根火柴，按此规律，搭 2021 个 六边形的图形需要_根火柴 18一个数字游戏： 第一步：取一个自然数 1 4n ，计算 2 1 1n 得 1 a； 第二步：算出 1 a的各位数字之和得 2 n，计算 2 2 1n
8、 得 2 a； 第三步：算出 2 a的各位数字之和得 3 n，计算 2 3 1n 得 3 a； 以此类推， 2020 a_ 19如图所示是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，按 照这样的规律，第4个图案中有_个涂有阴影的小正方形，第n个图案中有_个涂有阴影的小正 方形（用含有n的代数式表示） 20如图，有一个面积为 1 的正方形纸板，第一次剪掉这块正方形纸板的一半，第二次剪掉剩下的一半， 以此类推小明想到第n次剪掉的面积是 1 2n ，第n次剪掉后剩下的面积也是 1 2n ，小明受此启发，于是计 算出 2020 1111 2482 _ 21将长为40cm
9、，宽为15cm的长方形白纸，按如图所示的方法粘合起来，粘合部分宽为5cm，则4张白 纸粘合的总长度为_cm，则n张白纸粘合的总长度表示为_cm 22观察下列正三角形的三个顶点所标的数字规律，那么 2020 这个数在_个第三角形的_顶点处（第 二空填：上，左下，右下） 23下列是用火柴棒拼出的一列图形 仔细观察，找出规律，解答下列各题： （1）第 4 个图形中共有_根火柴，第 6 个图形中共有_根火柴； （2）第 n 个图形中共有_根火柴（用含 n 的式子表示） ； （3）请判断上组图形中前 2021 个图形火柴总数是 2021 的倍数吗？请说明理由 （参考： 1 1 23 2 nn n ，例如
10、求解 1 99 1 23945 2 ） 24如图是由一些火柴搭成的图案： （1）观察图案的规律，第 5 个图案需_根火柴； （2）照此规律，第 2021 个图案需要的火柴为多少根？ 25如图所示，用大小相等的小正方形拼大正方形，拼第 1 个正方形需要 4 个小正方形，拼第 2 个正方形 需要 9 个小正方形，按照这样的方法拼下去 （1）第 4 个正方形需要 个小正方形，第 5 个正方形需要 个小正方形； （2）第 m 个正方形比第（m1）个正方形多需要 个小正方形； （3）若第 n 个正方形比第（n1）个正方形多需要 21 个小正方形，求 n 的值 26如图是用大小相等的小五角星按一定规律拼成
11、的一组图案，第1个图案中有4颗五角星，第2个图案中 有7颗五角星，第3个图案中有10颗五角星，请根据你的观察完成下列问题 （1）根据上述规律，分别写出第4个图案和第5个图案中小五角星的颗数； （2）按如图所示的规律，直接写出第n个图案中小五角星的颗数； （用含n的代数式表示） （3）第 2021 个图案中有多少颗五角星？ 27用同样大小的两种不同颜色的正方形纸片，按下图方式拼正方形 第（1）个图形中有 1 个正方形； 第（2）个图形有 1+34 个小正方形； 第（3）个图形有 1+3+59 个小正方形； 第（4）个图形有 1+3+5+716 小正方形； （1）根据上面的发现我们可以猜想：1+3
12、+5+7+（2n1） （用含 n 的代数式表示） ； （2）请根据你的发现计算： 1+3+5+7+79； 81+83+85+399 参考答案参考答案 1A 2C 3C 4A 5A 6B 7C 8B 9A 10B 11A 12 4042 3 13 （1616，-2） 14505 15 2019 2 166062 1710106 1826 1917 4n+1 20 2020 1 1 2 21145 35n+5 22第 674 上 23 （1）17，25； （2）41n； （3）第 2021 个图形火柴总数是 2021 的倍数，理由见解析 24 （1）21； （2）8085 根 25 （1）25，36； （2） （2m1） ； （3）10 26 （1）第 4 个图案 13 颗；第 5 个图案 16 颗； （2）31n颗； （3）6064 颗 27 （1） 2 n ； （2） 1600； 38400
