1、2021 年中考数学一轮复习年中考数学一轮复习圆综合型选择题优生辅导训练圆综合型选择题优生辅导训练 1如图，RtABC 中，C90，AB5，cosA，以点 B 为圆心，r 为半径作B，当 r3 时，B 与 AC 的位置关系是（ ） A相离 B相切 C相交 D无法确定 2以坐标原点 O 为圆心，作半径为 2 的圆，若直线 yx+b 与O 相交，则 b 的取值范围是（ ） A0b2 B2 C22 D2b2 3在 RtABC 中，C90，BC3cm，AC4cm，以点 C 为圆心，以 2.5cm 为半径画圆，则C 与直 线 AB 的位置关系是（ ） A相交 B相切 C相离 D不能确定 4如图，在平面直
2、角坐标系 xOy 中，半径为 2 的P 的圆心 P 的坐标为（3，0） ，将P 沿 x 轴正方向平 移，使P 与 y 轴相切，则平移的距离为（ ） A1 B1 或 5 C3 D5 5已知O 的半径 r3，设圆心 O 到一条直线的距离为 d，圆上到这条直线的距离为 2 的点的个数为 m， 给出下列命题： 若 d5，则 m0；若 d5，则 m1；若 1d5，则 m3；若 d1，则 m2；若 d 1，则 m4其中正确命题的个数是（ ） A1 B2 C3 D5 6在平面直角坐标系 xOy 中，直线 l 经过点 A（3，0） ，点 B（0，） ，点 P 的坐标为（1，0） ，P 与 y 轴相切于点 O若
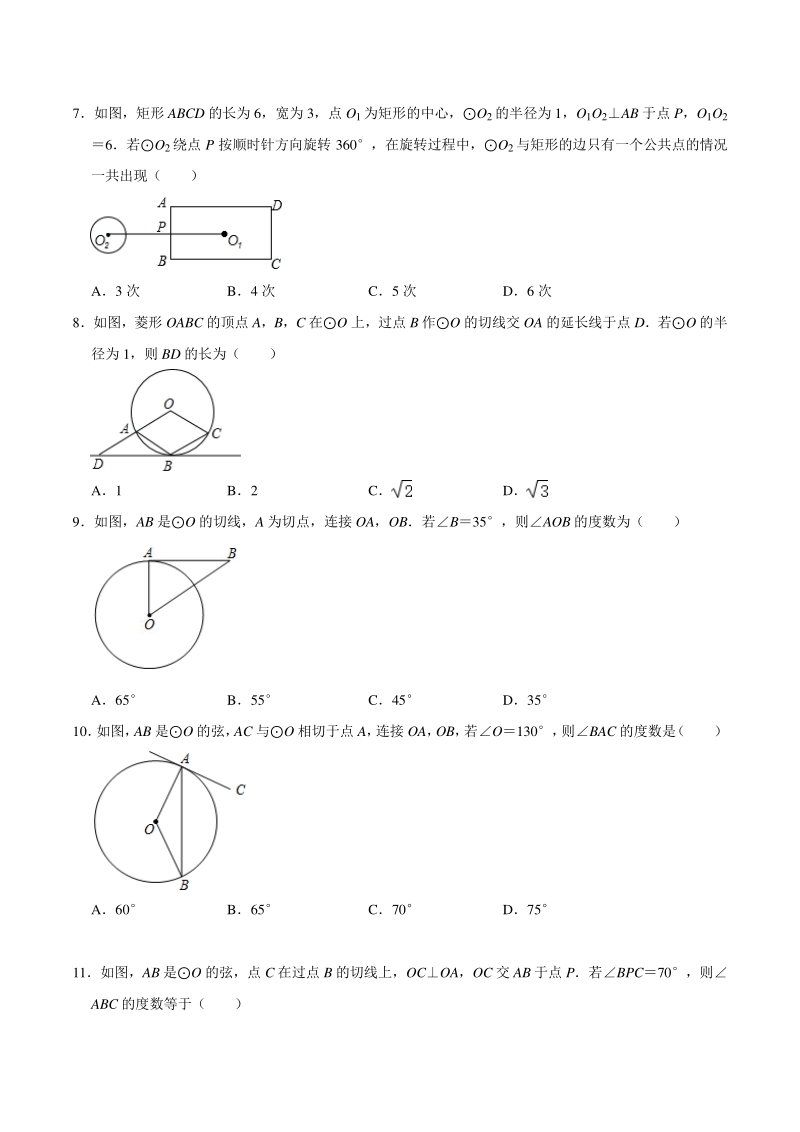
3、将P 沿 x 轴向左平移，平移后得到P（点 P 的对应点为点 P） ，当P与直 线 l 相交时，横坐标为整数的点 P共有（ ） A1 个 B2 个 C3 个 D4 个 7如图，矩形 ABCD 的长为 6，宽为 3，点 O1为矩形的中心，O2的半径为 1，O1O2AB 于点 P，O1O2 6若O2绕点 P 按顺时针方向旋转 360，在旋转过程中，O2与矩形的边只有一个公共点的情况 一共出现（ ） A3 次 B4 次 C5 次 D6 次 8如图，菱形 OABC 的顶点 A，B，C 在O 上，过点 B 作O 的切线交 OA 的延长线于点 D若O 的半 径为 1，则 BD 的长为（ ） A1 B2 C
4、 D 9如图，AB 是O 的切线，A 为切点，连接 OA，OB若B35，则AOB 的度数为（ ） A65 B55 C45 D35 10 如图， AB 是O 的弦， AC 与O 相切于点 A， 连接 OA， OB， 若O130， 则BAC 的度数是 （ ） A60 B65 C70 D75 11如图，AB 是O 的弦，点 C 在过点 B 的切线上，OCOA，OC 交 AB 于点 P若BPC70，则 ABC 的度数等于（ ） A75 B70 C65 D60 12如图，ABC 内接于圆，ACB90，过点 C 的切线交 AB 的延长线于点 P，P28则CAB （ ） A62 B31 C28 D56 13
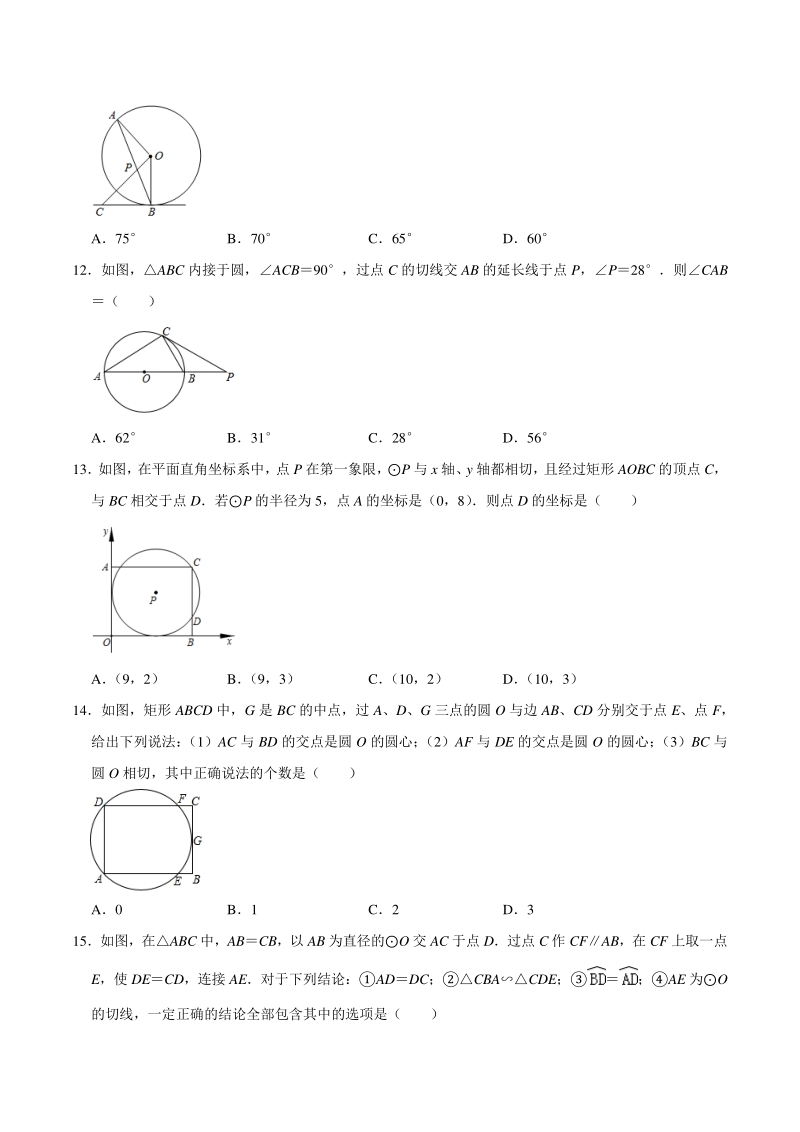
5、 如图， 在平面直角坐标系中， 点 P 在第一象限， P 与 x 轴、 y 轴都相切， 且经过矩形 AOBC 的顶点 C， 与 BC 相交于点 D若P 的半径为 5，点 A 的坐标是（0，8） 则点 D 的坐标是（ ） A （9，2） B （9，3） C （10，2） D （10，3） 14如图，矩形 ABCD 中，G 是 BC 的中点，过 A、D、G 三点的圆 O 与边 AB、CD 分别交于点 E、点 F， 给出下列说法： （1）AC 与 BD 的交点是圆 O 的圆心； （2）AF 与 DE 的交点是圆 O 的圆心； （3）BC 与 圆 O 相切，其中正确说法的个数是（ ） A0 B1 C2
6、 D3 15如图，在ABC 中，ABCB，以 AB 为直径的O 交 AC 于点 D过点 C 作 CFAB，在 CF 上取一点 E，使 DECD，连接 AE对于下列结论：ADDC；CBACDE；AE 为O 的切线，一定正确的结论全部包含其中的选项是（ ） A B C D 16如图，AB 是O 的直径，BC 交O 于点 D，DEAC 于点 E，要使 DE 是O 的切线，还需补充一个 条件，则补充的条件不正确的是（ ） ADEDO BABAC CCDDB DACOD 17如图，AB 是O 的直径，O 交 BC 的中点于 D，DEAC 于点 E，连接 AD，则下列结论正确的个数 是（ ） ADBC；E
7、DAB；OAAC；DE 是O 的切线 A1 个 B2 个 C3 个 D4 个 18如图，在O 中，E 是半径 OA 上一点，射线 EFOA，交圆于 B，P 为 EB 上任一点，射线 AP 交圆于 C，D 为射线 BF 上一点，且 DCDP，下列结论：CD 为O 的切线；PAPC；CDP2A， 其中正确的结论有（ ） A3 个 B2 个 C1 个 D0 个 19如图，在直角梯形 ABCD 中，ABBC，AD1，BC3，CD4，EF 为梯形的中位线，DH 为梯形的 高，则下列结论：BCD60；四边形 EHCF 为菱形；SBEHSCEH；以 AB 为直径的 圆与 CD 相切于点 F，其中正确结论的个
8、数为（ ） A4 B3 C2 D1 20矩形的两邻边长分别为 2.5 和 5，若以较长一边为直径作半圆，则矩形的各边与半圆相切的线段最多有 （ ） A0 条 B1 条 C2 条 D3 条 21 如图， P 为O 的直径 BA 延长线上的一点， PC 与O 相切， 切点为 C， 点 D 是O 上一点， 连接 PD 已 知 PCPDBC下列结论： （1）PD 与O 相切； （2）四边形 PCBD 是菱形； （3）POAB； （4）PDB120 其中正确的个数为（ ） A4 个 B3 个 C2 个 D1 个 参考答案参考答案 1解：RtABC 中，C90，AB5，cosA， ， AC4， BC3，
9、r3， BCr3， B 与 AC 的位置关系是相切， 故选：B 2解：当直线 yx+b 与圆相切，且函数经过一、二、四象限时，如图 在 yx+b 中，令 x0 时，yb，则与 y 轴的交点是（0，b） ， 当 y0 时，xb，则 A 的交点是（b，0） ， 则 OAOB，即OAB 是等腰直角三角形 连接圆心 O 和切点 C则 OC2 则 OBOC2即 b2； 同理，当直线 yx+b 与圆相切，且函数经过二、三、四象限时，b2 则若直线 yx+b 与O 相交，则 b 的取值范围是2b2 故选：D 3解：过 C 作 CDAB 于 D，如图所示： 在 RtABC 中，C90，AC4，BC3， AB5
10、， ABC 的面积ACBCABCD， 345CD， CD2.42.5， 即 dr， 以 2.5 为半径的C 与直线 AB 的关系是相交； 故选：A 4解：当P 位于 y 轴的左侧且与 y 轴相切时，平移的距离为 1； 当P 位于 y 轴的右侧且与 y 轴相切时，平移的距离为 5 故选：B 5解：若 d5 时，直线与圆相离，则 m0，故正确； 若 d5 时，直线与圆相离，则 m1，故正确； 若 1d5，则 m2，故错误； 若 d1 时，直线与圆相交，则 m3，故错误； 若 d1 时，直线与圆相交，则 m4，故正确 故选：C 6解：如图所示，点 P 的坐标为（1，0） ，P 与 y 轴相切于点 O
11、， P 的半径是 1， 若P 与 AB 相切时，设切点为 D，由点 A（3，0） ，点 B（0，） ， OA3，OB，由勾股定理得：AB2，DAM30， 设平移后圆与直线 AB 第一次相切时圆心为 M（即对应的 P） ， MDAB，MD1，又因为DAM30， AM2，M 点的坐标为（1，0） ，即对应的 P点的坐标为（1，0） ， 同理可得圆与直线第二次相切时圆心 N 的坐标为（5，0） ， 所以当P与直线 l 相交时，横坐标为整数的点 P的横坐标可以是2，3，4 共三个 故选：C 7解：如图，O2与矩形的边只有一个公共点的情况一共出现 4 次， 故选：B 8解：连接 OB， 四边形 OABC
12、 是菱形， OAAB， OAOB， OAABOB， AOB60， BD 是O 的切线， DBO90， OB1， BDOB， 故选：D 9解：AB 是O 的切线， OAAB， OAB90， AOB90B55， 故选：B 10解：AC 与O 相切于点 A， ACOA， OAC90， OAOB， OABOBA O130， OAB25， BACOACOAB902565 故选：B 11解：OCOA， AOC90， APOBPC70， A907020， OAOB， OBAA20， BC 为O 的切线， OBBC， OBC90， ABC902070 故选：B 12解：连接 OC，如图， PC 为切线， OC
13、PC， PCO90， POC90P902862， OAOC， AOCA， 而POCA+OCA， A6231 故选：B 13解：设O 与 x、y 轴相切的切点分别是 F、E 点，连接 PE、PF、PD，延长 EP 与 CD 交于点 G， 则 PEy 轴，PFx 轴， EOF90， 四边形 PEOF 是矩形， PEPF，PEOF， 四边形 PEOF 为正方形， OEPFPEOF5， A（0，8） ， OA8， AE853， 四边形 OACB 为矩形， BCOA8，BCOA，ACOB， EGAC， 四边形 AEGC 为平行四边形，四边形 OEGB 为平行四边形， CGAE3，EGOB， PEAO，A
14、OCB， PGCD， CD2CG6， DBBCCD862， PD5，DGCG3， PG4， OBEG5+49， D（9，2） 故选：A 14解：连接 DG、AG，作 GHAD 于 H，连接 OD，如图， G 是 BC 的中点， AGDG， GH 垂直平分 AD， 点 O 在 HG 上， ADBC， HGBC， BC 与圆 O 相切； OGOD， 点 O 不是 HG 的中点， 圆心 O 不是 AC 与 BD 的交点； ADFDAE90， AEF90， 四边形 AEFD 为O 的内接矩形， AF 与 DE 的交点是圆 O 的圆心； （1）错误， （2） （3）正确 故选：C 15解：AB 为直径，
15、 ADB90， BDAC， 而 ABCB， ADDC，所以正确； ABCB， 12， 而 CDED， 34， CFAB， 13， 1234， CBACDE，所以正确； ABC 不能确定为直角三角形， 1 不能确定等于 45， 与不能确定相等，所以错误； DADCDE， 点 E 在以 AC 为直径的圆上， AEC90， CEAE， 而 CFAB， ABAE， AE 为O 的切线，所以正确 故选：D 16解：当 ABAC 时，如图：连接 AD， AB 是O 的直径， ADBC， CDBD， AOBO， OD 是ABC 的中位线， ODAC， DEAC， DEOD， DE 是O 的切线 所以 B 正
16、确 当 CDBD 时，AOBO，OD 是ABC 的中位线， ODAC DEAC DEOD DE 是O 的切线 所以 C 正确 当 ACOD 时，DEAC，DEOD DE 是O 的切线 所以 D 正确 故选：A 17解：AB 是直径， ADB90， ADBC，故正确； 连接 DO， 点 D 是 BC 的中点， CDBD， ACDABD（SAS） ， ACAB，CB， ODOB， BODB， ODBC，ODAC， ODECED， ED 是圆 O 的切线，故正确； 由弦切角定理知，EDAB，故正确； 点 O 是 AB 的中点，故正确， 故选：D 18解：DCDP， DPCDCP， DPCAPE， D
17、CPAPE， OAOC， OACOCA； OAC+APE90， OCA+DCP90， CD 为O 的切线（正确） ； 不一定； 连接 CO， CD 是O 的切线， DCPAOC DCP（1802A） ， 又DCP（180CDP） ， 1802A180CDP， CDP2A，正确 故选：B 19解：在 RtDCH 中，CD4，CHCBBH2， DCH60，即BCD60， 在四边形 EHCF 中，又 CHEF2，CHEF，CFCD2， 四边形 EHCF 是菱形， SBEHBHEB1EBEB， SCEHCHEB2EBEB， SBEHSCEH 以 AB 的直径的圆的半径为，而 EF2，REF 所以 AB
18、 为直径的圆与 CD 不相切于点 F 则正确 故选：B 20解：以较长的边为直径作圆，半径正好与另一边相等，所以如上图可知，与半圆相切的线段有 3 条 故选 D 21解： （1）连接 CO，DO， PC 与O 相切，切点为 C， PCO90， 在PCO 和PDO 中， ， PCOPDO（SSS） ， PCOPDO90， PD 与O 相切， 故（1）正确； （2）由（1）得：CPBBPD， 在CPB 和DPB 中， ， CPBDPB（SAS） ， BCBD， PCPDBCBD， 四边形 PCBD 是菱形， 故（2）正确； （3）连接 AC， PCCB， CPBCBP， AB 是O 直径， ACB90， 在PCO 和BCA 中， ， PCOBCA（ASA） ， POAB， 故（3）正确； （4）四边形 PCBD 是菱形，CPO30， DPDB，则DPBDBP30， PDB120， 故（4）正确； 正确个数有 4 个， 故选：A
