2021年中考数学一轮复习《圆综合型解答题》优生辅导训练（含答案）

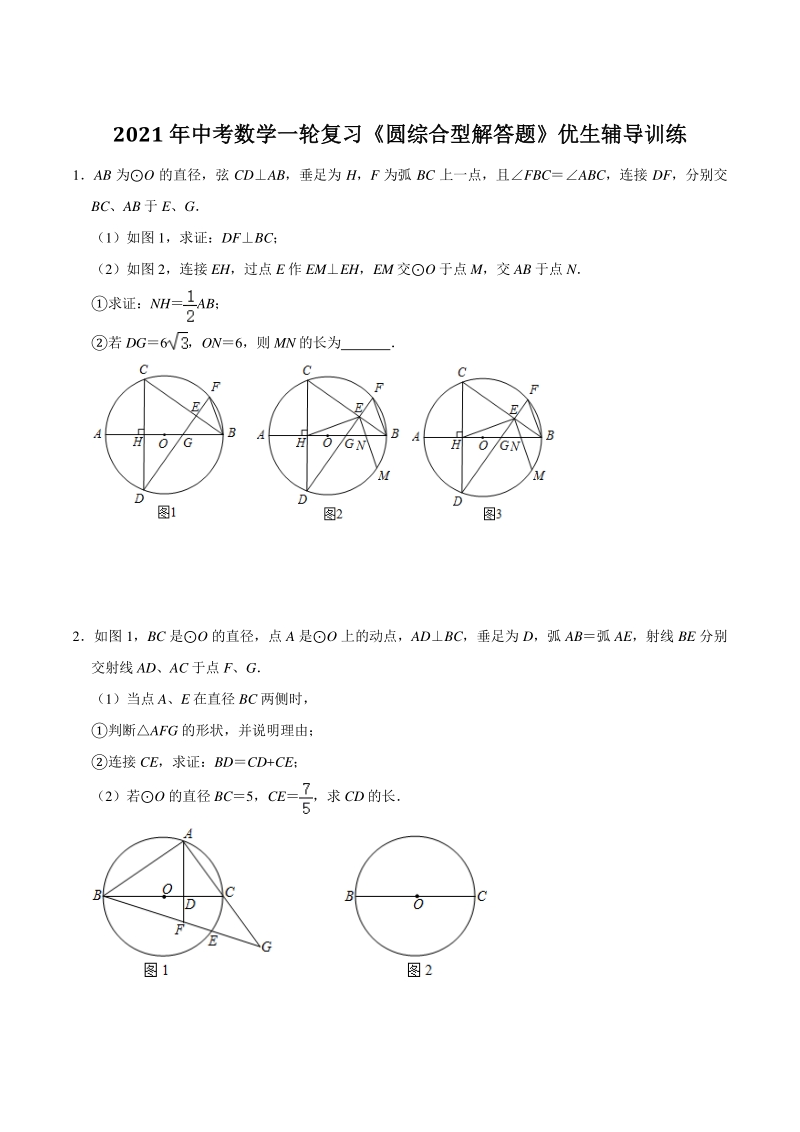
1、2021 年中考数学一轮复习年中考数学一轮复习圆综合型解答题优生辅导训练圆综合型解答题优生辅导训练 1AB 为O 的直径，弦 CDAB，垂足为 H，F 为弧 BC 上一点，且FBCABC，连接 DF，分别交 BC、AB 于 E、G （1）如图 1，求证：DFBC； （2）如图 2，连接 EH，过点 E 作 EMEH，EM 交O 于点 M，交 AB 于点 N 求证：NHAB； 若 DG6，ON6，则 MN 的长为 2如图 1，BC 是O 的直径，点 A 是O 上的动点，ADBC，垂足为 D，弧 AB弧 AE，射线 BE 分别 交射线 AD、AC 于点 F、G （1）当点 A、E 在直径 BC 两

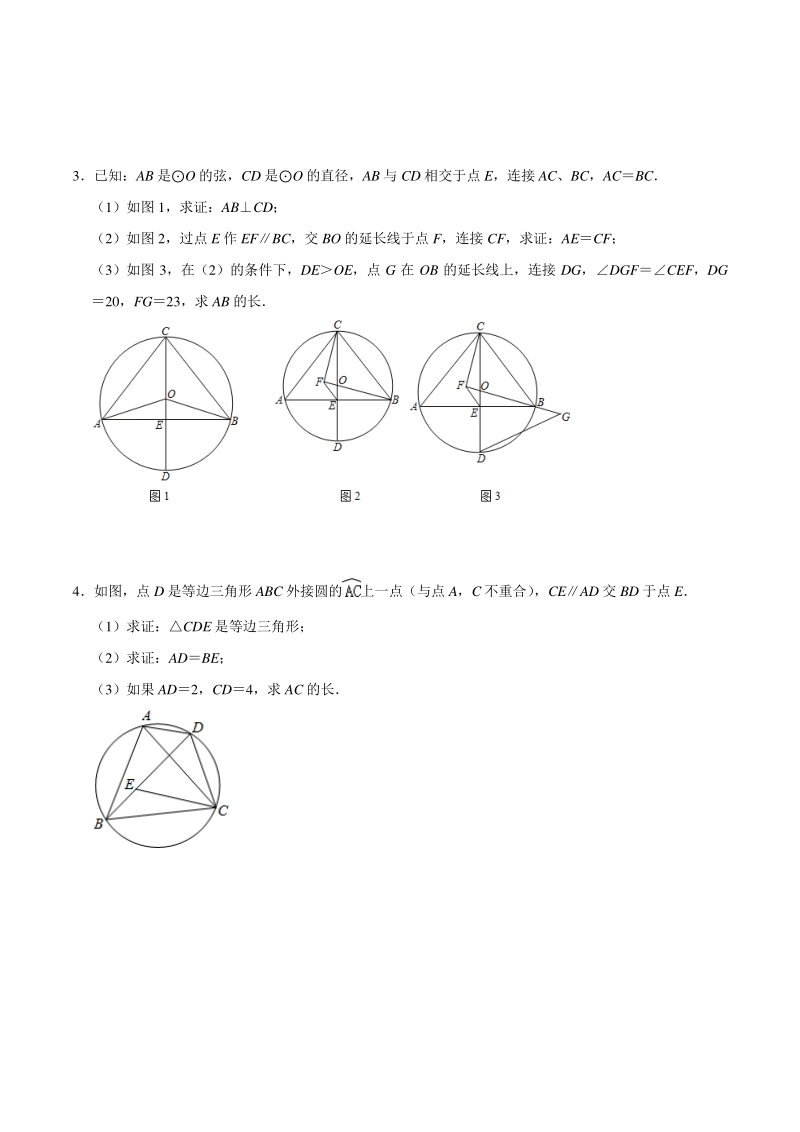
2、侧时， 判断AFG 的形状，并说明理由； 连接 CE，求证：BDCD+CE； （2）若O 的直径 BC5，CE，求 CD 的长 3已知：AB 是O 的弦，CD 是O 的直径，AB 与 CD 相交于点 E，连接 AC、BC，ACBC （1）如图 1，求证：ABCD； （2）如图 2，过点 E 作 EFBC，交 BO 的延长线于点 F，连接 CF，求证：AECF； （3）如图 3，在（2）的条件下，DEOE，点 G 在 OB 的延长线上，连接 DG，DGFCEF，DG 20，FG23，求 AB 的长 4如图，点 D 是等边三角形 ABC 外接圆的上一点（与点 A，C 不重合） ，CEAD 交 BD

3、 于点 E （1）求证：CDE 是等边三角形； （2）求证：ADBE； （3）如果 AD2，CD4，求 AC 的长 5已知：ABC 内接于O，BAC 的角平分线 AD 交O 于点 D （1）如图，以点 D 为圆心，DB 长为半径作弧，交 AD 于点 I求证：点 I 是ABC 的内心； （2）如图，在（1）的条件下，若 AD 与 BC 交于点 E求证：； （3）探究：如图，ABC 内接于O，若 BC8，BAC120，求ABC 内切圆半径的最大值 6如图，在 RtABC 中，ACB90，A30，O 为 AB 上一点，以 O 为圆心，OB 为半径的圆与 AC 相切于点 E，交 AB 于点 D，连接

4、BE、OE，连接 DE 并延长交 BC 的延长线于点 H （1）求ABE 的度数； （2）求证：OABH； （3）已知O 的半径为 2，请直接写出阴影部分的面积 7正方形 ABCD 的四个顶点都在O 上，E 是O 上的一点 （1）如图，若点 E 在上，F 是 DE 上的一点，DFBE求证：ADFABE； （2）在（1）的条件下，小明还发现线段 DE、BE、AE 之间满足等量关系：DEBEAE请说明理 由； （3）如图，若点 E 在上，连接 DE，CE，已知 BC5，BE1，求 DE 及 CE 的长 8如图，AB 为O 的弦，点 P 在O 上，PAPB，PC 为O 的直径，过点 P 作 PQAB

5、，垂足为点 Q （1）说明APCQPB； （2） 若O 的半径为 7， 点 P 在O 上， 点 Q 在O 内， 且 PQ4， 过点 Q 作 PQ 的垂线交O 于点 A、 B设 PAx，PBy， 求 y 与 x 的函数表达式，并写出 x 的取值范围 若 PA 和 PB 的值恰好是两个连续的整数，求线段 AC 的长 9如图，O 为等边ABC 的外接圆，半径为 2，点 D 在劣弧上运动（不与点 A，B 重合） ，连接 DA，DB， DC （1）求证：DC 是ADB 的平分线； （2）设四边形 ADBC 的面积为 S，线段 DC 的长为 x，试用含 x 的代数式表示 S； （3）若点 M，N 分别在线

6、段 CA，CB 上运动（不含端点） ，经过探究发现，点 D 运动到每一个确定的位 置，DMN 的周长有最小值 t，随着点 D 的运动，t 的值会发生变化，求所有 t 值中的最大值 10如图，AB 为O 直径，半径为 2，点 D 为弧 AB 的中点，点 C 在O 上由点 A 顺时针向点 B 运动（点 C 不与点 A，点 B 重合） ，连接 AC，BC，CD，AD，BD （1）求证：CD 是ACB 的角平分线； （2）求 CD 的长 x 的取值范围（直接写出答案） （3） 四边形 ADBC 的面积 S 是线段 CD 的长 x 的函数吗？如果是， 求出函数解析式， 并求出 S 的最大值， 如果不是，

7、请说明理由 11如图，四边形 ABCD 内接于O，ABAD，对角线 BD 为O 的直径，AC 与 BD 交于点 E点 F 为 CD 延长线上，且 DFBC （1）证明：ACAF； （2）若 AD2，AF，求 AE 的长； （3）若 EGCF 交 AF 于点 G，连接 DG证明：DG 为O 的切线 12如图，O 是 RtABC 的外接圆，ABC90，弦 BDBA，BEDC 交 DC 的延长线于点 E （1）求证：BC 平分ECA； （2）求证：BE 是O 的切线； （3）若 CE1，BE3，求 DE 的长 13如图，AB 是半圆 O 的直径，C 是的中点，点 D 在上，AC、BD 相交于点 E，

8、F 是 BD 上一点，且 BFAD （1）求证：CFCD； （2）连接 AF，若CAF2ABF； 求证：ACAF； 当ACF 的面积为 12 时，求 AC 的长 14 如图， O 的内接四边形 ABCD 两组对边的延长线分别交 BC、 DC 于点 E， F， 设Ex， Fy （1）当 AC 为直径时，求证：xy； （2）当 x+y60 时 求DAB 的度数； 连接 OA，过点 O 作 OHAB 于 H，当 AB2OH 时，求DAO 度数 15如图，已知ABC 中，ACB90，ACBC3，D 是射线 AB 上一点，作BCD 的外接圆O， CE 是O 的直径，连接 DE、BE （1）若点 D 在

9、AB 边上，求DCE 的度数； （2）若ACD 与BDE 全等，求 AD 的长； （3）若 AD，求O 的半径 r 的值 16如图，在 RtABC 中，ACB90，D 为 AB 边上的一点，以 AD 为直径的O 交 BC 于点 E，过点 C 作 CGAB 交 AB 于点 G，交 AE 于点 F，过点 E 作 EPAB 交 AB 于点 P，EADDEB （1）求证：BC 是O 的切线； （2）求证：CEEP； （3）若 CG12，AC15，求四边形 CFPE 的面积 17如图，已知四边形 ABCD 内接于O，AC 是O 的直径，DCDB，延长 CD 交直线 BA 于点 E，过点 D 作 DFAB

10、，交直线 AB 于点 F （1）若ACD35，求CAD 的度数； （2）求证：直线 DF 为O 的切线； （3）若 BC8，AD5，求 AB 的长 18如图，AB 为O 的直径，C 为O 上的一点，连接 AC、BC，ODBC 于点 E，交O 于点 D，连接 CD、AD，AD 与 BC 交于点 F，CG 与 BA 的延长线交于点 G （1）求证：ACDCFD； （2）若CDAGCA，求证：CG 为O 的切线； （3）若 sinCAD，求 tanCDA 的值 19如图 1，已知O 与ABC 的边 BC、AC 分别相切于点 D、E，BO 是ABC 的平分线，与O 相交于 点 G （1）求证：直线 A

11、B 是O 的切线； （2）已知O 的半径为 2，如图 2，点 F 是 AB 与O 的切点，连接 OF、FG、DG，若 OFDG 求证：四边形 OFGD 是菱形； 求阴影部分的面积 20在平面直角坐标系 xOy 中，过点 N（6，1）的两条直线 l1，l2，与 x 轴正半轴分别交于 M、B 两点， 与 y 轴分别交于点 D、A 两点，已知 D 点坐标为（0，1） ，A 在 y 轴负半轴，以 AN 为直径画P，与 y 轴的另一个交点为 F （1）求 M 点坐标； （2）如图 1，若P 经过点 M 判断P 与 x 轴的位置关系，并说明理由；求弦 AF 的长； （3）如图 2，若P 与直线 l1的另一

12、个交点 E 在线段 DM 上，求NE+AF 的值 21如图，点 O 是ABC 中 AB 边上一点，以点 O 为圆心，OA 的长为半径作O，O 恰好经过点 C，且 与边 BC，AB 分别交于 E，F 两点连接 AE，过点 E 作O 的切线，交线段 BF 于点 M，交 AC 的延长 线于点 N，且 EMBM，EBAO （1）求EAM 的度数； （2）求证：AC22BMOB； （3）若 OA，求CNE 的面积 22已知矩形 ABCD 中，AB2，AD5，点 E 是 AD 边上一动点，连接 BE、CE，以 BE 为直径作O，交 BC 于点 F，过点 F 作 FHCE 于 H （1）当直线 FH 与O

13、相切时，求 AE 的长； （2）当 FHBE 时，求 AE 的长； （3）若线段 FH 交O 于点 G，在点 E 运动过程中，OFG 能否成为等腰直角三角形？如果能，求出 此时 AE 的长；如果不能，说明理由 23如图，AB 是O 的直径，AC 是弦，点 E 在圆外，OEAC 于 D，BE 交O 于点 F，连接 BD，BC， CF，BFCAED （1）求证：AE 是O 的切线； （2）求证：BODEOB； （3）设BOD 的面积为 S1，BCF 的面积为 S2，若 tanODB，求的值 24等边三角形 ABC 内接于O，点 D 在弧 AC 上，连接 AD、CD、BD （1）如图 1，求证 BD

14、 平分ADC； （2）如图 2，若DBC15，求证：AD：AC：； （3）如图 3，若 AC、BD 交于点 E，连接 OE，且 OE2，若 BD3CD，求 AD 的长 参考答案参考答案 1 （1）证明：CDAB， BHC90， C+ABC90， FBCABC，FC， F+FBC90， BEF90， DFBC （2）证明：连接 OC OCOB， OCBOBCD， CDAB， CHO90，CHDH， CEDBEF90， HECDCHDH， DHED， OCBHED， EMEH， HENHED+DEN90， DEN+BENBED90， HEDBEN， OCBBEN， OCEM， COHHNE， 在C

15、OH 与HNE 中， ， COHHNE（AAS） ， CONH， NHAB （3）解：连接 OM，过点 M 作 MPAB 于点 P HENHEG+GEN90， D+DGH90， DHEG， GENDGH， DGHEGN， GENEGN， ENGN， COHHNE， OHNEGN， HGOH+OGGN+OGON6， DG6，DHG90， HECHDH6， DHGBHC， ， BH12， 设 OBOCr，则 OHBHOB12r， OH2+CH2OC2， （12r）2+（6）2r2， 解得：r9， OM9，NHAB9，NGENBN3， MNPHNE，MPNHEP90， MNPHNE， ， 设 MNa

16、，则 NP，MPa， OPON+NP6+， OP2+MP2OM2， （6+）2+（a）292， 解得：a19（舍去） ，a25， MN5 故答案为 5 2 （1）解：等腰三角形，理由如下； BC 为O 的直径， BAC90， ABE+AGB90， ADBC， ADC90， ACD+DAC90， 弧 AE弧 AB， ABEACD， DACAGB， FAFG， FAG 是等腰三角形； 证明：在 CB 上截取 DHCD，连接 AH、AE，如图 1 所示： ADBC， AHAC， AHCACH， 弧 AB弧 AE， AEBABE，AEAB， AHC+ACH+HAC180，ABE+AEB+BAE180，

17、ACBAEB， HACBAE， CAEHAB， ACEAHB（SAS） ， CEHB， BDDH+HB， BDCD+CE； （2）解：分两种情况： 当点 A、E 在直径 BC 两侧时，如图 1 所示： 由（1）得：BDCD+CECD+， BD+CDBC5， CD+CD5， 解得：CD； 当点 A、E 在直径 BC 同侧时， 在 CB 上截取 DHBD，连接 AH、AE，如图 2 所示： 弧 AB弧 AE， ACEACHAEB，ABAE， ADBC， ABC+BAD90， BADHAD， BC 是O 的直径， BECBAC90， ABC+ACB90， BADACB， AHCADH+HAD90+H

18、AD，AECBEC+AEB， AHCAEC， 在AHC 和AEC 中， ， AHCAEC（AAS） ， CHCE， DHBD（BCCH）（5）， CDCH+DH； 综上所述，CD 的长为或 3解： （1）如图 1，ACBC，AOBO，COCO， AOCBOC（SSS） ， ACOBCO， CEAB， 即 ABCD； （2）如图 2，COOB， OCBOBC， EFBC， OFEOBC，OEFOCB， OFEOEF， OEOF， BFBO+OFCO+OECE， 而 BCBC，CBFBCE， CEBBFC（SAS） ， CEBCFB90，EBFC， 而 AEBE， AECF； （3）过点 D 作

19、DMFG 于点 M， OMDCFB90，COFMOD，OCOD， CFODMO（AAS） ， DMCF， 又GEFBFBCBCE，DMGCFB90， FCBMDG（AAS） ， BCDG20，GMBF， FMBG，则 FOBG， 设 FOx，则 BG2x，则 BF232x，COBO233x， CF2BC2BF2202（232x）2，CF2CO2FO2（233x）2x2， 即 202（232x）2（233x）2x2，解得 x（舍去）或， CF12， 则 AB2AE2CF24 4 （1）证明：ABC 为等边三角形， BACACB60， BDCBAC60，ADBACB60， CEAD， DECADB

20、60， DCEDECBDC60， CDE 为等边三角形； （2）证明：ABC 和CDE 为等边三角形， BCAC，CECD， BCE+ACEACD+ACE60， BCEACD， 在BCE 和ACB 中， ， BCEACD（SAS） ， BEAD； （3）解：过点 C 作 CFAD 于 F， CDFABC60， DCF30， DFCD2， AF4， CF2CD2DF2422212， AC 5 （1）证明：如图中，连接 BI DBDI， DBIDIB， DIBIAB+IBA，DBIIBC+DBC， 又DBCDACDAB， DBCIAB， IBAIBC，即 BI 平分ABC， 点 I 是ABC 的内

21、心 （2）证明：如图中， BDABCA，DBCDAC， BDEACE， ， DBDI， （3）解：如图中，作BAC 的角平分线 AD 交O 于 D，连接 BD，DC，以 D 为圆心，DB 为半径作 作弧，交 AD 于点 I， 由（1）点 I 是ABC 的内心 IHAC， IH 是ABC 的内切圆的半径， 在AIH 中，IAHBAC60， IHAI，故欲求 IH 的最大值只要求出 AI 的最大值， DBCDAC60，DCBDAB60， BDC 是等边三角形， DBCB8，即 DI8， 作直径 DF， 在 RtBDF 中，DFB60，DB8， DF，即直径为， AI 的最大值为8， ABC 的内切

22、圆的半径的最大值为 84 6解： （1）AC 与圆相切，故 OEAC， 在 RtAOE 中，AOE90A60， OBOE， ABEOEBAOE30； （2）在 RtAOE 中，A30，则 AO2OE， 在DBH 中，点 O 是 BD 的中点，OEBH， 故 OE 是DBH 的中位线， 故 OEBH， 即 OABH； （3）在AOE 中，OE2AO， 则 AEOEtanAOE2， 则阴影部分的面积SAOES扇形ODE22222 7解： （1）由圆周角定理得，ADFABE， 四边形 ABCD 是正方形， ADAB，BAD90， 在ADF 和ABE 中， ， ADFABE（SAS） ； （2）ADF

23、ABE， AEAF，EABFAD， BAD90， EAF90， AEF 为等腰直角三角形， EFAE， DEBEAE； （3）如图，过点 B 作 BHCE 于点 H， 四边形 ABCD 为正方形，故BEC45，DEC45， 在BEC 中，BE1，BC5，BEC45， 则 BHBEsinEBC1sin45EH， 在 RtBCH 中，CH， ECEH+CH4； 在EDC 中，DEC45，CE4，CDBC5， 连接 BD，则 BD5， BCD90， BD 是O 的直径， BED90， BE1， DE7 8解： （1）PQAB，则PQB90， PC 是圆的直径，则PAC90PQB， PBQPCA， A

24、PCQPB； （2）APCQPB， 则，即， 则 y（4x2） ； （3），即， 则 APPB56， 若 PA 和 PB 的值恰好是两个连续的整数，则 PA7，PB8， 在 RtPBQ 中，BQ4， ，即， 解得 AC7 9解： （1）ABC 是等边三角形， ABCBACACB60， ADCABC60，BDCBAC60， ADCBDC， DC 是ADB 的平分线； （2）四边形 ADBC 的面积 S 是线段 DC 的长 x 的函数， 理由如下： 如图 1，将ADC 绕点 C 逆时针旋转 60，得到BHC， CDCH，DACHBC， 四边形 ACBD 是圆内接四边形， DAC+DBC180， D

25、BC+HBC180， 点 D，点 B，点 H 三点共线， DCCH，CDH60， DCH 是等边三角形， 四边形 ADBC 的面积 SSADC+SBDCSCDHCD2， Sx2（2x4） ； （3）如图 2，作点 D 关于直线 AC 的对称点 E，作点 D 关于直线 BC 的对称点 F， 点 D，点 E 关于直线 AC 对称， EMDM， 同理 DNNF， DMN 的周长DM+DN+MNFN+EM+MN， 当点 E，点 M，点 N，点 F 四点共线时，DMN 的周长有最小值， 则连接 EF，交 AC 于 M，交 BC 于 N，连接 CE，CF，DE，DF，作 CP EF 于 P， DMN 的周

26、长最小值为 EFt， 点 D，点 E 关于直线 AC 对称， CECD，ACEACD， 点 D，点 F 关于直线 BC 对称， CFCD，DCBFCB， CDCECF，ECFACE+ACD+DCB+FCB2ACB120， CPEF，CECF，ECF120， EPPF，CEP30， PCEC，PEPCEC， EF2PEECCDt， 当 CD 有最大值时，EF 有最大值，即 t 有最大值， CD 为O 的弦， CD 为直径时，CD 有最大值 4， t 的最大值为 4 10 （1）证明：点 D 为的中点， ， ACDBCD， CD 是ACB 的角平分线 （2）解：， ADDB， AB4，AB 是直径

27、 ADB90， ADBD2， 点 C 在上运动， 当点 C 与 A 或 B 重合时，CD 的值最小，最小值为 2， 当 CD 是直径时，CD 的值最大，最大值为 4， 点 C 不与点 A，点 B 重合， 2x4 （3）解：是的 理由：如图，作 DECB 于 E 点，作 DFAC 的延长线于 F 点， DEBDFC90， 又CD 是ACB 的角平分线， DFDE， ADBC 是圆内接四边形， FADDBE， AFBBED（AAS） ， AFBE， AC+BCCF+CE2CF， 又AB 是直径， ACB90， ACDBCD45， CFCEDFDE， AC+BC2DF， 四边形 ADBC 的面积 S

28、ACDF+BCDE（AC+BC）DFDF2（CD）2x2， 开口向上，对称轴为 y 轴， 当 x4 时，S 有最大值8 11 （1）证明：四边形 ABCD 内接于O， ABC+ADC180 ADF+ADC180， ABCADF 在ABC 与ADF 中， ， ABCADF（SAS） ACAF； （2）解：由（1）得，ACAF ABAD， ADEACD DAECAD， ADEACD ， 则 AE； （3）证明：EGCF， AGAE 由（2）得， DAGFAD， ADGAFD ADGF ACAF， ACDF 又ACDABD， ADGABD BD 为O 的直径， BAD90 ABD+BDA90 ADG

29、+BDA90 GDBD DG 为O 的切线 12解： （1）BDBA， BDABAD， BCABDA， BCABAD， 四边形 BCDA 是O 的内接四边形， BCEBAD，即 CB 是ECA 的角平分线； （2）连结 OB，OD， 在ABO 和DBO 中， ， ABODBO（SSS） ， DBOABO， ABOOABBDC， DBOBDC， OBED， BEED， EBBO， BE 是O 的切线； （3）BE 是O 的切线， 则EBC+CBO90， CBA90CBO+OBA， EBCOBACABBDE， BECBED90， BECDEB， ，即， 解得 DE9 13 （1）证明：AB 是直径

30、， ACB90， C 是的中点， ， ACCB， CBFCAD，BFAD， CBFCAD（SAS） ， BCFACD， FCDACB90， CFCD （2）证明：过点 A 作 AGCF 于点 G，则FGAFCD90， AGCD， CAGACDABF， CAF2ABF， CAF2CAG，即CAGFAG， CAG+ACG90，FAG+AFG90， ACGAFG， ACAF 过点 A 作 AGCF 于点 G，过点 B 作 BHCF 交 CF 的延长线于点 H则BHCCGA90 CAG+GCA90， BCH+GCA90， BCHCAG， CBCA， BCHCAG（AAS） ， CHAG，BHCG， F

31、CD90，CFCD， CFDCDF45， BHF90， BFH45FBH， BHHF， HFCG， ACAF，AGCF， CF2CG， AGCH3CG， 设 CGx，则 CF2x，AG3x， 则有，SACFCFAG2x3x12， x2 或2（舍弃） ， CG2，AG6， AGC90， AC2 14证明： （1）AC 是直径， ADCABC90， ADCE+DCE，ABCF+BCF， E+DCEF+BCF， 又DCEBCF， EF， xy； （2）四边形 ADCB 是圆内接四边形， ADF+ABE180， E+DAB+EBA180，F+DAB+ADF180， E+DAB+EBA+F+DAB+AD

32、F360， E+F+2DAB180， DAB60； 如图， OHAB， AHBH， AB2OH， AHOHBH， OAHOBH45， DAODABOAH15 15解： （1）ABC 中，ACB90，ACBC3， CABCBA45， CE 是O 的直径， CDE90CBE， CBDCED45， DCE45； （2）ABC 中，ACB90，ACBC3， AB3， DCEDEC45， DCDE， ACD 与BDE 全等，且 CDDE，CABDBEDCE45， BDAC3， ADABBD33， 当点 D 在线段 AB 的延长线上时，同理可求 ADAB+BD3+3； （3）如图，过点 E 作 EFBD

33、于 F， AB3，AD， BD2， EFBD，DBE45， FEB45DBE， EFBF，BEEF， BDEBCE，EFDEBC90， DEFCEB， ， 即，解得：BF， BEBF1， CE， OECO， O 的半径 r 的值为 16证明： （1）连接 OE， OEOD， OEDADE， AD 是直径， AED90， EAD+ADE90， 又DEBEAD， DEB+OED90， BEO90， OEBC， BC 是O 的切线 （2）BEOACB90， ACOE， CAEOEA， OAOE， EAOAEO， CAEEAO， AE 为CAB 的角平分线， 又EPAB，ACB90， CEEP； （3

34、）连接 PF， CG12，AC15， AG9， CAEEAP， AECAFGCFE， CFCE， CEEP， CFPE， CGAB，EPAB， CFEP， 四边形 CFPE 是平行四边形， 又CFPF， 四边形 CFPE 是菱形， CFEPCEPF， CAEEAP，EPAACE90，CEEP， ACEAPE（AAS） ， APAC15， PGAPAG1596， PF2FG2+GP2， CF2（12CF）2+36， CF， 四边形 CFPE 的面积CFGP645 17 （1）解：AC 是直径， ADC90， CAD90ACD903555 （2）证明：连接 DO，并延长 DO 交 BC 于点 T

35、DBDC， ， DTBC，CTBT， DTB90， AC 是直径， CBA90， DFBE， DFB90， 四边形 DFBT 是矩形， TDF90， ODDF， DF 是O 的切线 （3）解：四边形 DFBT 是矩形， DFBT， CTBTBC4， DFBT4， AFD90，AD5， AF3， 设 EFx，DEy，则有， 解得 x（负根已经舍弃） ， EF， DBDC， DBCDCB， CBE90， DBC+DBE90，DCB+E90， DBEE， DBDE， DFBE， FBFE， ABFBAF3 18 （1）证明：ODBC， ， CADFCD， 又ADCCDF， ACDCFD； （2）证明

36、：连接 OC，如图 1 所示： AB 是O 的直径， ACB90， ABC+CAB90， OBOC， OBCOCB， CDAOBC，CDAGCA， OCBGCA， OCGGCA+OCAOCB+OCA90， CGOC， OC 是O 的半径， CG 是O 的切线； （3）解：连接 BD，如图 2 所示： CADCBD， ODBC， sinCADsinCBD，BECE， 设 DEx，ODOBr，则 OErx，BD3x 在 RtBDE 中，BE， BC2BE， 在 RtOBE 中，OE2+BE2OB2， 即（rx）2+（）2r2， 解得：rx， AB2r9x， 在 RtABC 中，AC2+BC2AB2

37、， AC2+（）2（9x）2， AC7x 或 AC7x（舍去） ， tanCDAtanCBA 19 （1）证明：如图 1，作 OFAB 于 F， O 与 BC 相切于点 D， ODBC， BO 是ABC 的平分线，ODBC，OFAB， OFOD， 直线 AB 是O 的切线； （2）证明：BF、BD 是O 的两条切线， OFBODB90，OBFOBD， BOFBOD， OFDG BOFOGD， OGDBOD， OGGDOD， 同理可得，OFFGGDOD， 四边形 OFGD 是菱形； 解：OGGDOD， OGD 为等边三角形， BOD60， OBD30， OB2OD2， 由勾股定理得，BD2， 阴

38、影部分的面积OBD 的面积扇形 DOG 的面积222 20解： （1）设直线 l1的表达式为 ykx+b，将点 D、N 的坐标代入上式得，解得， 故直线 l1的表达式为 yx+1， 令 yx+10，解得 x3， 故点 M（3，0） ； （2）相切，理由： 连接 PM、AM，过点 P 作 PNOA 于点 N， 由点 D、M、N 的坐标知，点 M 是 DN 的中点， 而 AN 是圆的直径，故 AMMN，则AND 为等腰三角形， 故 AM 平分DAB，即DAMNAM， PMPA，故MABAMPDAM， PMy 轴，即 PMx 轴， 故P 与 x 轴的位置关系是相切； 由由直线 l1的表达式知，tan

39、DMO，则 tanOAM3， 故设直线 AM 的表达式为 y3x+b，将点 M 的坐标代入上式得：033+b，解得 b9， 故点 A（0，9） ， 由点 A、N 的坐标得，AN10，则圆的半径为 5， 在 RtAPN 中，AP5，PNOM3，则 AN4， 则 AF2AN8； （3）连接 AE，则 AEMN，过点 F 作 FGAE 于点 G，作 FHMN 于点 H， 连接 FN，则 FNy 轴，则点 F（0，1） ， 由直线 l1的表达式知，该直线倾斜角的正切值为，即 tanDMO， DHODOM90，则DFHDMO，设DFHDEO，则 tan，则 sin， AEDN，FHDN，则 FHAE，故

40、DAE， 在 RtAFG 中，FGAFsinAF， 则NE+AF（NE+AF）（NE+EH）HN， 在 RtFDH 中，DHDFsin（1+1） ， 由点 DN 的坐标得，ND2， 则 HNDNHD2， 故NE+AFHN18 21解： （1）连接 OE， 直线 MN 与O 相切于点 E， OEMN， OEM90， EOM+EMO90， EMBM， BBEM， 在O 中，AOEO，EBAO， EBEO， BEOM， EMOB+BEM2B， EOM+EMOB+2B3B， 3B90， B30， EOMB30， 在O 中，EAMEOM3015； （2）证明：连接 CO，在O 中，COEO， CEOEO

41、M+B2B60， CEO 是等边三角形， EOCOCE，COE60， COBEOM+COE30+6090， COA90， 在O 中，OAOC， 在 RtAOC 中，ACOA， AC22OA2， 由（1）可知，BBEMEOM，BB， BEMBOE， ， BE2BMBO， EBAO， AO2BMBO， AC22AO2， AC22BMOB； （3）解：过点 N 作 NPCE 于点 P， 在 RtOEM 中，OEOA，EOM30， EMBM1，OM2， 由（2）可知，AOC 为等腰直角三角形， NAF45， 在ANM 中ANM180NAFNMA180453075， NCENAF+B45+3075， N

42、CEANM， NECE， 由（2）可知，CEO 是等边三角形， NECEOEOA， NECBEM30， 在 RtNPE 中，NPsinNECNEsin30， SCNECENP 22解： （1）如图 1，连接 EF，FA， FH 为圆的切线且又和 EC 垂直， CEAF CEFAFE； 又AFEFEB， CEFBEF， EF 为BEC 的平分线； EFB90， EFBC， BECE BEC 为等腰三角形， BF 为 BC 的一半； EACF， 四边形 CEAF 为平行四边形， 即 AECF2.5； （2）解：FHBE，FHCE， BECE， AEB+DEC90， ABE+AEB90， ABEDE

43、C， AD90， ABEDEC， ， AB2，AD5， CDAB2， ， AE1 或 AE4 （3）连接 EF、OF、OG，如图 3 所示： 则BFE90， 设 AEx，则 EF，AB2，BFAEx，CFDE5x， 若OFG 是等腰直角三角形，则FOG90， 连接 BG、EG，设 BG、EF 交于点 K， BFK 和EGK 都是等腰直角三角形， BFKFx，BKx，EK2KF2x， 在等腰直角EGK 中，根据勾股定理得：GKEG（2x） ，BGGK+BK（2+x） ， 又EBGEFGFCH， BEGCEF， ，即， 解得：x，或 x（舍去） ， AE 的长度是 23解： （1）BFCAED，

44、AB 是O 的直径， BFCBAC， AEDBAC， OEAC 于 D， ADE90， AED+DAE90， BAC+DAE90， AB 是O 的直径， AE 是O 的切线； （2）ADOE， OAEODA90， AEDOAD， AODEOA， ， OA2ODOE， OBOA， OB2ODOE， ， 又BODEOB， BODEOB； （3）AB 是O 的直径， ACB90， OEAC 于 D， OEBC， ODBDBC， 在直角三角形 BCD 中，tanODBtanDBC， 设 CDk，BC3k， BDk， BODEOB， OBDOEB， OEBC， OEBFBC， OBDFBC， BACBF

45、C， ABDFBC， （）2（）2， O 是 AB 的中点， SABD2S1， 24解： （1）ABC 为等边三角形，则ABCACBBAC60， BDCBAC60，ADCACB60BDC， BD 平分ADC； （2）过点 A 作 AHBD 于点 H， 在 RtAHD 中，ADH60，设 AD2a，则 AHa，HDa， ABC60，DBC15， ABH601545， 为等腰直角三角形，则 ABAHaAC， AD：AC：； （3）设 CDm，在 DB 上截取 DFCD，连接 CF， BDC60，故CDF 为等边三角形，则 CDDFCFm，DFC60， 则 BD3CD3m，则 BF2m， BFC18

46、0DFC120ADC， FCCD，FBCCAD， BFCADC（AAS） ， ADBF2m， DFCADB60， FCAD， AEDCEF，故2， 设 EC2t，则 AE4t，AC6t，SGCG3t，故 GEt， 连接 AO，过点 O 作 OGAC 于点 G， ABC 为等边三角形，则OAG30， 在 RtAOG 中，OGAGtanOAG3tt， 在 RtOGE 中，OGt，GEt，OE2， 由勾股定理得： （t）2+t2（2）2，解得 t， 则 AC6； 过点 A 作 CD 的垂线交 CD 的延长线于点 K， 在 RtADK 中，ADK180ADC60，AD2m，则 DKm，AKm， 在 RtAKC 中，AKm，KCKD+CDm+m2m，AC6， 由勾股定理得： （m）2+（2m）2（6）2，解得 m6， 则 AD2m12