 陕西省西安市八校2020-2021学年高考数学第二次联考试卷(理科)含答案解析
陕西省西安市八校2020-2021学年高考数学第二次联考试卷(理科)含答案解析
《陕西省西安市八校2020-2021学年高考数学第二次联考试卷(理科)含答案解析》由会员分享,可在线阅读,更多相关《陕西省西安市八校2020-2021学年高考数学第二次联考试卷(理科)含答案解析(16页珍藏版)》请在七七文库上搜索。
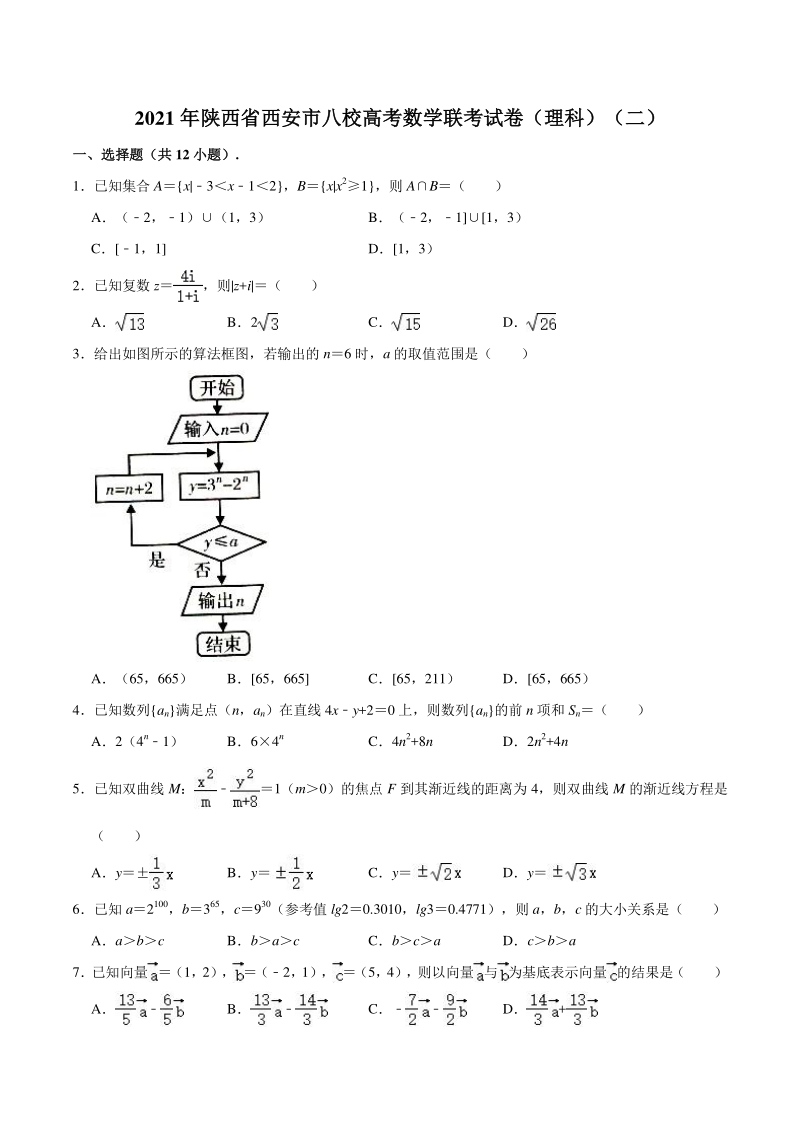
1、2021 年陕西省西安市八校高考数学联考试卷(理科)(二)年陕西省西安市八校高考数学联考试卷(理科)(二) 一、选择题(共一、选择题(共 12 小题)小题). 1已知集合 Ax|3x12,Bx|x21,则 AB( ) A(2,1)(1,3) B(2,11,3) C1,1 D1,3) 2已知复数 z,则|z+i|( ) A B2 C D 3给出如图所示的算法框图,若输出的 n6 时,a 的取值范围是( ) A(65,665) B65,665 C65,211) D65,665) 4已知数列an满足点(n,an)在直线 4xy+20 上,则数列an的前 n 项和 Sn( ) A2(4n1) B64n
2、 C4n2+8n D2n2+4n 5已知双曲线 M:1(m0)的焦点 F 到其渐近线的距离为 4,则双曲线 M 的渐近线方程是 ( ) Ay By Cy Dy 6已知 a2100,b365,c930(参考值 lg20.3010,lg30.4771),则 a,b,c 的大小关系是( ) Aabc Bbac Cbca Dcba 7已知向量 (1,2), (2,1), (5,4),则以向量 与 为基底表示向量 的结果是( ) A B C D+ 8已知数列an+2n是等比数列,且 a10,a24,则数列 a6( ) A1984 B1920 C992 D960 9函数 f(x)的零点的个数是( ) A1
3、 B2 C3 D4 10若(2+x2)6a0+a1x2+a2x4+a3x6+a4x8+a5x10+a6x12,则 a0+a5( ) A88 B86 C76 D66 11一个由橡皮泥制作的空间几何体的三视图如图,三个视图的外边框都是边长为 6 的正方形,各边上的 交点为边的中点将该几何体揉搓成一个球体(不计损耗),则该球体的半径为( )(圆周率 取 3) A36 B4 C3 D 12已知在线段 AB 上有 C、D 两点,满足 AC40cm,CD120cm,DB20cm,点 P 在线段 CD 上运动, 设 M 为 AP 的中点,N 为 CD 的中点(如图),则的值( ) A等于 1 B等于 2 C
4、等于 3 D与 P 的位置有关 二、填空题(共二、填空题(共 4 小题,每小题小题,每小题 5 分,共分,共 20 分。)分。) 13已知随机变量 B(5,),则 P(3) (用数字作答) 14已知角 的顶点是直角坐标系 xOy 的原点,始边与 x 轴的非负半轴重合,若 P(4,3)是 的终边 上一点,则 sin2 15已知椭圆 C:1(ab0)左、右焦点分别为 F1、F2,过 F1且倾斜角为 30的直线 l1与过 F2的直线 l2交于 P 点,点 P 在椭圆上,且F1PF290则椭圆 C 的离心率 e 16已知可导函数 f(x)的定义域为(0,+),满足 xf(x)2f(x)0,且 f(2)
5、4,则不等式 f(2x) 4x的解集是 三、解答题(共三、解答题(共 5 小题,共小题,共 70 分。解答应写出文字说明,证明过程或演算步骤。第分。解答应写出文字说明,证明过程或演算步骤。第 1721 题为必考题,题为必考题, 第第 22、23 题为选考题题为选考题,考生根据要求作答。)考生根据要求作答。) 17已知函数 f(x)sinxcosx(0)的最大值为 2,且 f(x)的最小正周期为 ()若 x0,求 f(x)的最小值和最大值; ()设ABC 的内角 A、B、C 的对应边分别为 a、b、c,D 为 AC 的中点,若 am,BD,f ()0,求ABC 的面积 SABC 18已知抛物线
6、E:yx2的焦点为 F,过 y 轴正半轴上一点 M 的直线 l 与抛物线 E 交于 A、B 两点,O 为 坐标原点,且2 ()求证:直线 l 过定点; ()设点 F 关于直线 OB 的对称点为 C,求四边形 OABC 面积的最小值 19如图,在三棱锥 DABC 中,侧面ABD 是边长为 6 的等边三角形,底面ABC 是角 C 为 120的等 腰三角形,CD ()求证:平面 ABD平面 ABC; ()若 M 在 CD 上,且 CMMD,求二面角 MABD 的余弦值 20中国悠久文化之一“石头、尖刀、布”游戏,留传至今,仍然是人们喜爱的一种比胜负的游戏方式 “石 头”即拳头,“尖刀”即食指和中指,
7、“布”即手掌,“石头”胜“尖刀”,“尖刀”胜“布”,“布” 胜“石头”现在有甲、乙、丙三人玩“石头、尖刀、布”游戏比胜负,假定每个人每次伸出什么手势 是随机的并且是均等的(一次游戏,可以仅一人获胜或两人同时获胜或不分胜负,不分胜负即三人手 势均相同或互不相同) ()若进行一次“石头、尖刀、布”游戏,求仅甲获胜的概率和有两人同时获胜的概率; ()若进行一次“石头、尖刀、布”游戏,仅一人获胜时,获胜者得 5 分,失败者各得分2;有 2 人同时获胜时,获胜者各得 3 分,失败者得2 分;不分胜负时,各得 0 分现在进行两次“石头、尖 刀、布”游戏,用 X 表示甲所得的总分数,求 X 的分布列和期望
8、21设函数 f(x)2ax+ln(2x1)(aR) ()讨论 f(x)的单调性; ()当 a1 时,求证:f(x)(2x1)e2x1(e 为自然对数的底数) (二)选考题:共(二)选考题:共 10 分分.请考生在第请考生在第 22、23 题中任选一题作答,如果多做,则按所做的第一题计分题中任选一题作答,如果多做,则按所做的第一题计分.选修选修 4-4:坐标系与参数方程:坐标系与参数方程 22已知极坐标系与直角坐标系的极点与原点重合,极轴与 x 轴的非负半轴重合,有相同的单位长度曲 线 S 的极坐标方程为 4cos2sin,直线 l 的参数方程为(t 为参数,a1) ()求曲线 S 的长度; (
9、)若直线 l 被曲线 S 截得的线段长为 4,求实数 a 的集合 选修选修 4-5:不等式选讲:不等式选讲 23已知 f(x)|x3|2|x+1|+x ()解不等式 f(x)1; ()求证:xR,对a、b(0,+),a+b2,不等式f(x)成立 参考答案参考答案 一、选择题(共一、选择题(共 12 小题)小题). 1已知集合 Ax|3x12,Bx|x21,则 AB( ) A(2,1)(1,3) B(2,11,3) C1,1 D1,3) 解:Ax|2x3,Bx|x1 或 x1, AB(2,11,3) 故选:B 2已知复数 z,则|z+i|( ) A B2 C D 解:z, z+i+i+i2i(1
10、i)+i2i+2+i2+3i, 故|z+i|, 故选:A 3给出如图所示的算法框图,若输出的 n6 时,a 的取值范围是( ) A(65,665) B65,665 C65,211) D65,665) 解:模拟程序的运行,可得 n0,y1 满足判断框内的条件,执行循环体,n2,y5 满足判断框内的条件,执行循环体,n4,y65 满足判断框内的条件,执行循环体,n6,y665 因为输出的 n 的值为 6, 所以 n6 时 ya,即 665a,n4 时 ya,即 65a, 故 a 的取值范围是65,665) 故选:D 4已知数列an满足点(n,an)在直线 4xy+20 上,则数列an的前 n 项和
11、 Sn( ) A2(4n1) B64n C4n2+8n D2n2+4n 解:数列an满足点(n,an)在直线 4xy+20 上, 可得 an4n+2,an+1an4,a16, 所以数列an是等差数列,首项为 6,公差为 4, 所以数列an的前 n 项和 Sn6n+ 2n2+4n 故选:D 5已知双曲线 M:1(m0)的焦点 F 到其渐近线的距离为 4,则双曲线 M 的渐近线方程是 ( ) Ay By Cy Dy 解:双曲线 M:1(m0)的焦点 F 到其渐近线的距离为 4, 由双曲线的一个焦点坐标(,0),一条渐近线方程为:, 可知:4,即 m+816,解得 m8, 所以双曲线的渐近线方程为:
12、yx 故选:C 6已知 a2100,b365,c930(参考值 lg20.3010,lg30.4771),则 a,b,c 的大小关系是( ) Aabc Bbac Cbca Dcba 解:a2100,b365,c930(参考值 lg20.3010,lg30.4771), lgalg2100100lg230.10, lgblg36565lg3650.477131.0115, lgclg930lg36060lg3600.477128.626, a,b,c 的大小关系为:bac 故选:B 7已知向量 (1,2), (2,1), (5,4),则以向量 与 为基底表示向量 的结果是( ) A B C D+
13、 解:设 x +y , 即(5,4)x(1,2)+y(2,1), 则,得 x,y, 即 , 故选:A 8已知数列an+2n是等比数列,且 a10,a24,则数列 a6( ) A1984 B1920 C992 D960 解:因为 a10,a24, 所以 a1+212,a2+228, 又数列an+2n是等比数列,故公比 q4, 所以 a6+26245211, 故 a6211261984 故选:A 9函数 f(x)的零点的个数是( ) A1 B2 C3 D4 解:函数 f(x)的零点就是0,函数的零点的个数,也就是方程根的个数 即 2xx21,x1,而 x22x10,40,所以方程由两个解,并且不是
14、1 所以函数 f(x)的零点的个数是 2 故选:B 10若(2+x2)6a0+a1x2+a2x4+a3x6+a4x8+a5x10+a6x12,则 a0+a5( ) A88 B86 C76 D66 解:令 x0 得 a02664, a5为 x10的系数,即 a5212, 则 a0+a564+1276, 故选:C 11一个由橡皮泥制作的空间几何体的三视图如图,三个视图的外边框都是边长为 6 的正方形,各边上的 交点为边的中点将该几何体揉搓成一个球体(不计损耗),则该球体的半径为( )(圆周率 取 3) A36 B4 C3 D 解:根据几何体的三视图可知该几何体为一个棱长为 6 的正方体,切去四个角


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 陕西省 西安市 2020 2021 学年 高考 数学 第二次 联考 试卷 理科 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-175164.html