1、20212021 年年中考中考摸底考试数学试卷摸底考试数学试卷 注意事项：1.本试卷共 8 页，总分 120 分，考试时间 120 分钟. 2.答题前，考生务必将姓名、准考证号填写在试卷和答题卡相应位置上. 3.答选择题时，每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑；答非选择题时，将答 案写在答题卡上，写在本试卷上无效. 4.考试结束后，将本试卷和答题卡一并交回. 一、选择题（本大题有 16 个小题，共 42 分.1-10 小题各 3 分，1116 小题各 2 分.在每小题给出的四个选项 中，只有一项是符合题目要求的） 1.如图 1，有两种说法： 线段AB的长是点A到点B
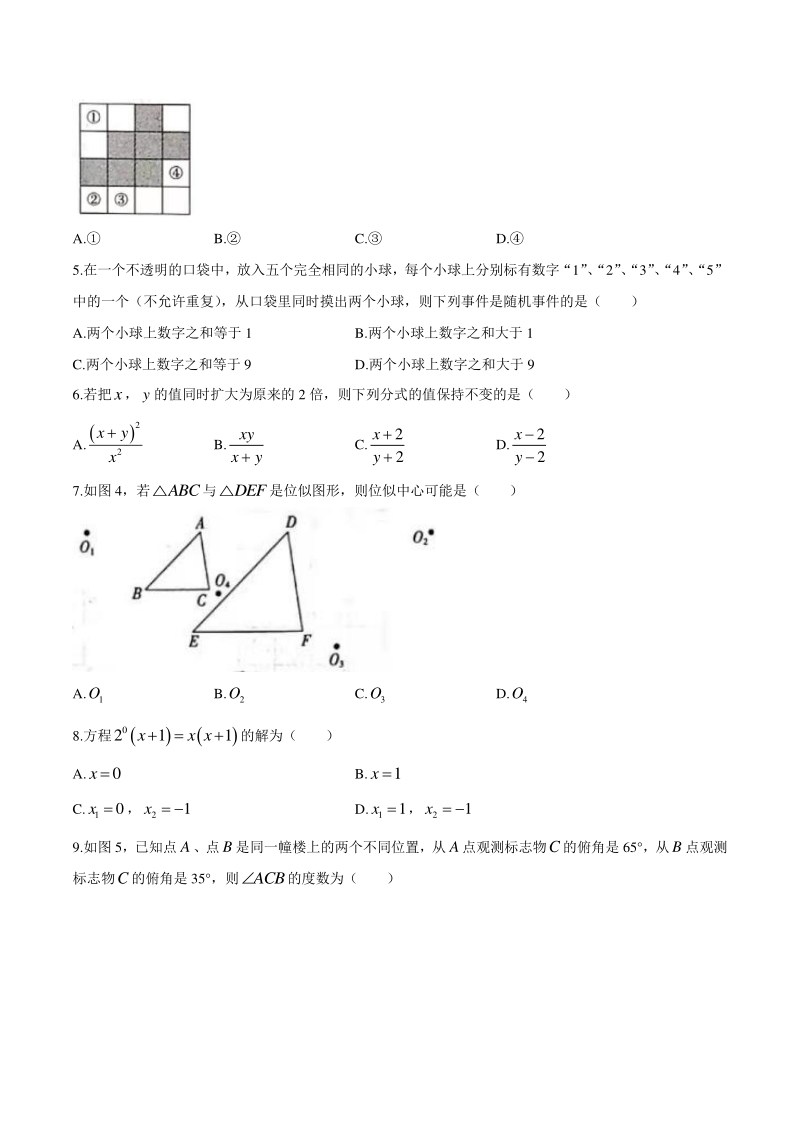
2、的距离 线段AB的长是直线 1 l、 2 l之间的距离 关于这两种说法，正确的是（ ） A.正确，错误 B.正确，正确 C.错误，正确 D.错误，错误 2.如图 2，在数轴上，注明了四段的范围，若某段上有两个整数，则这段是（ ） A.段 B.段 C.段 D.段 3.若0.00018 n 14444 424 L L444 4 3 个 用科学记数法表示为 10 1.8 10，则n的值是（ ） A.9 B.10 C.11 D.12 4.图 3 是4 4的网格图，将图中标有、的一个小正方形涂灰，使所有的灰色图形构成中心对 称图形，则涂灰的小正方形是（ ） A. B. C. D. 5.在一个不透明的口袋
3、中，放入五个完全相同的小球，每个小球上分别标有数字“1” 、 “2” 、 “3” 、 “4” 、 “5” 中的一个（不允许重复） ，从口袋里同时摸出两个小球，则下列事件是随机事件的是（ ） A.两个小球上数字之和等于 1 B.两个小球上数字之和大于 1 C.两个小球上数字之和等于 9 D.两个小球上数字之和大于 9 6.若把x，y的值同时扩大为原来的 2 倍，则下列分式的值保持不变的是（ ） A. 2 2 xy x B. xy xy C. 2 2 x y D. 2 2 x y 7.如图 4，若ABC与DEF是位似图形，则位似中心可能是（ ） A. 1 O B. 2 O C. 3 O D. 4
4、O 8.方程 0 211xx x的解为（ ） A.0 x B.1x C. 1 0 x ， 2 1x D. 1 1x ， 2 1x 9.如图 5，已知点A、点B是同一幢楼上的两个不同位置，从A点观测标志物C的俯角是 65 ，从B点观测 标志物C的俯角是 35 ，则ACB的度数为（ ） A.25 B.30 C.35 D.65 10.若 222 95190 55991k ，则k的值是（ ） A.100 B.199 C.200 D.299 11.证明：平行四边形的对角线互相平分 已知：如图 6，四边形ABCD是平行四边形，对角线AC，BD相交于点O 求证：OAOC，OBOD 证明：四边形ABCD是平行
5、四边形， ABOCDO，BAODCO， AOBCOD， OAOC，OBOD 其中，在“四边形ABCD是平行四边形”与“ABOCDO，BAODCO”之间应补充的步骤 是（ ） A.ABCD，ADBC B./AD BC，ADBC C./AB CD，/AD BC D./AB CD，ABCD 12.把图 7 所示的正方形展开，得到的平面展开图可以是（ ） A B C D 13.船工小王驾驶一艘小艇匀速从甲港向乙港航行，离开甲港后不久便发现有重要物品落在甲港，小王马上 驾驶小艇以相同的速度驰回甲港，到达甲港后，因找重要物品耽误了一段时间，为了按时到达乙港，小王 回乙港时，加快了航行速度，则小艇离乙港的距
6、离y与时间t之间的函数关系的大致图象是（ ） A B C D 14.如图 8，在ABC中，作以A为内角，四个顶点都在ABC边上的菱形时，如下的作图步骤是打乱 的. 分别以点A，G为圆心，大于 1 2 AG的长为半径在AG的两侧作弧，两弧相交于点M，N； 作直线MN分别交AB，AC于点P，Q，连接PG，GQ； 分别以点D，E为圆心，大于 1 2 DE的长为半径作弧，两弧相交于ABC内一点F，连接AF并延长 交边BC于点G； 以点A为圆心，小于AC长为半径作弧，分别交AB，AC于点D，E. 则正确的作图步骤是（ ） A. B. C. D. 15.嘉淇用一些完全相同的ABC纸片，已知六个ABC纸片按
7、照图 9-1 所示的方法拼接可得外轮廓是正 六边形图案，若用n个ABC纸片按图 9-2 所示的方法拼接，那么可以得到外轮廓的图案是（ ） 图 1 图 2 A.正十二边形 B.正十边形 C.正九边形 D.正八边形 16.对于题目： “已知0,2A，3,2B，抛物线 2 31210ymxmxmm与线段AB（包含端 点A、B） 只有一个公共点， 求m的取值范围” .甲的结果是30m ， 乙的结果是 3 0 2 m， 则 （ ） A.甲的结果正确 B.乙的结果正确 C.甲、乙的结果合在一起才正确 D.甲、乙的结果合在一起也不正确 二、填空题（本大题有 3 个小题，共 12 分.1718 小题各 3 分
8、；19 小题有 3 个空，每空 2 分） 17.计算312 . 18.如图 10，ABC沿AC平到ABC ，A B 交BC于点D，若6AC ，D是BC的中点，则 CC . 19.如图 11-1，有一个足够长的矩形纸片ABCD，E、F分别是AD、BC上的点，24DEF. 图 1 图 2 图 3 （1）将纸片含CD的部分沿EF折叠，称为第 1 次操作；如图 11-2，则 CFG ； （2）继续将纸片含CD的部分沿BF折叠，称为第 2 次操作；如图 11-3，则CFE ；以后，重复 上述这两步操作，分别记作第 3 次，第 4 次，第 5 次第n操作，则n的最大值为 . 三、解答题（本大题有 7 个小
9、题，共 66 分.解答应写出文字说明、证明过程或验算步骤） 20.（本小题满分 8 分） 利用运算律计算有时可以简便 例 1：2 5 6 172 6 5 178 2214 ； 例 2：99 9999 100 19900 999801. 请你参考黑板中老师的讲解，用运算律简便计算. （1） 11 123 22 ； （2）计算： 2215 4646 3737 . 21.（本小题满分 8 分） 已知两个整式 2 2Axx，B 2x，其中系数被污染. （1）若是2，化简 2 222xxx ； （2）若2x时，AB的值为 18. 说明原题中是几？ 若再添加一个常数a，使A，B，a的和不为负数，求a的最小
10、值. 22.（本小题满分 9 分） 在中考理化实验操作中，初三某班除两名同学因故外全部参加考试，考试结束后，把得到的成绩（均为整 数分，满分 10 分）进行统计并制成如图 12-1 所示的条形统计图和如图 12-2 所示的扇形统计图（不完整）. 图 1 图 2 （1）m ； （2）若从这些同学中，随机抽取一名整理一下实验器材，求恰好抽到成绩不小于 8 分同学的概率； （3）若两名同学经过补测，把得到的成绩与原来成绩合并后，发现成绩的中位数发生改变，求这两名同学 的成绩和. 23.（本小题满分 9 分） 如图 13，已知正方形ABCD，点P在对角线AC上，过点P作PEAC交边BC于点E（点E不与
11、B、 C重合） ，延长BC至点F，使得CFBE，连接DF. （1）求证：EFPCDP； （2）若 1 2 CFDF，求APD的度数； （3）若点O是CDP的内心，连接OD、OC直接写出COD的取值范围. 24.（本小题满分 10 分） 如图 14，已知直线 1 l，经过点0,3B、点2, 3C，交x轴于点D，点P是x轴上一个动点，过点C、P 作直线 2 l. （1）求直线 1 l的表达式； （2）已知点7,0A，当 1 3 DPCACD SS 时，求点P的坐标； （3）设点P的横坐标为m，点 11 ,M x y， 22 ,N x y是直线 2 l上任意两个点，若 12 xx时，有 12 yy，
12、 请直接写出m的取值范围. 25.（本小题满分 10 分） 如图 15-1，在RtABC中，90C，10AB，6BC ，O是AC的中点，以点O为圆心在AC的 右侧作半径为 3 的半圆O，分别交AC于点D、E，交AB于点G、F. 图 1 图 2 思考：连接OF，若OFAC，求AF的长度； 探究：如图 15-2，将线段CD连同半圆O绕点C旋转. （1）在旋转过程中，求点O到AB距离的最小值； （2）若半圆O与RtABC的直角边相切，设切点为K，连接AK，求AK的长. 26.（本小题满分 12 分） 在新型冠状肺炎疫情期间，某农业合作社决定对一种特色水果开展线上销售，考虑到实际情况，一共开展 了 3
13、0 次线上销售，综合考虑各种因素，该种水果的成本价为每吨 2 万元，销售结束后，经过统计得到了如 下信息： 信息 1：设第x次线上销售水果y（吨） ，且第一次线上销售水果为 39 吨，然后每一次总比前一次销售减少 1 吨； 信息 2：该水果的销售单价p（万元/吨）均由基本价和浮动价两部分组成，其中基本价保持不变，第 1 次 线上销售至第 15 次线上销售的浮动价与销售场次x成正比，第 16 次线上销售至第 30 次线上销售的浮动价 与销售场次x成反比； 信息 3： x（次） 2 8 24 p（万元） 2.2 2.8 3 请根据以上信息，解决下列问题. （1）求y与x之间的函数关系式； （2）若
14、3.2p （万元/吨） ，求x的值； （3）在这 30 次线上销售中，哪一次线上销售获得利润最大？最大利润是多少？ 2020-2021 学年度第二学期九年级摸底考试学年度第二学期九年级摸底考试 数学答案数学答案 1-6 7-12 ADBCDB 13-16 BDCD 17. 1 2 18.3 19.132 ，108 ，6 20.解： （1）原式 11 132523 22 （2） 2215 4646 3737 . 2125 4466 3377 2125 46 3377 4 610 21.解： （1） 222 2222222xxxxxxx （2）设m，依题意得， 2 22 22218m 解之得，4m
15、 由于18AB，所以A、B、a的和不为负数时有0ABa. 即180a，解之得，18a，所以a的最小值为18. 22.解： （1）10 （2）一共有4 6 11 12 740 （名）同学，其中成绩不小于 8 分同学有 30 名同学 所以P（抽到成绩不小于 8 分同学） 3 4 （3）当两名同学成绩不大于 8 时，新成绩的中位数不会发生改变，均为 8 当两名同学成绩大于或等于 9 时，新成绩的中位数为 8.5，发生改变， 因此两名同学的成绩和为 18 或 19 或 20 23.（1）证明：四边形ABCD是正方形，AC是对角线 45ACBACD，BCCD PEAC于P，交BC于点E，45PECPCE
16、，PEPC BECF，EFECCFECBEBCCD 45FEPDCP，EFPCDP （2）在RtDCF中， 1 2 CFDF， 1 sin 2 CF CDF DF ，30CDF EFPCDP，PFPD，EPFCPD，90DPFCPE 45PDFPFD， 15PDC，75ADP，45DAC，60APD （3）135157.5COD 24.解： （1）设直线 1 l的解析式为0ykxb k 0,3B、点2, 3C在直线 1 l上， 3 32 b kb ， 解之得， 3 3 k b 33yx （2）直线33yx 交x轴于D，1,0D，7,0A，6AD， 过点C作CEx轴于E，2, 3C，3CE ，
17、1 9 2 ACD SAD CE 1 3 DPCACD SS ，3 DPC S ，设点,0P x， 1 133 2 DPC Sx 3x 或1x，P的坐标3,0或1,0 （3）2m 25.解：思考：如图 15-1，在RtABC中，90C，10AB，6BC ，8AC O是AC的中点，4AOCO，OFAC，3OF 5AF 探究： （1）如图 15-2，当CDAB时，点O到AB的距离最小 由三角形面积公式可得， 11 22 ABC SACBCAB CG 24 5 CG ， 4 5 OGCGOC 点O到AB距离的最小值是 4 5 （2）当半圆O与BC相切时，如图 15-3，设切点为K，连接OK，AK，则
18、90OKC 在RtOCK中，3OK ，4OC ，7CK 在RtACK中，8AC ，71AK 当半圆O与AC相时，如图 15-4，设切点为K，连接OK，90OKC 在RtOCK中，3OK ，4OC ，7CK 87AK AK的长为71或87 26.解： （1）40yx （2）设第 1 场第 15 场时p与x的函数关系式为paxb；第 16 场第 30 场时p与x的函数关系式为 m pb x 依题意得 2.22 2.88 ab ab ，解这个方程组得， 1 10 2 a b ， 1 2 10 px 又当24x时，有32 24 m ，解之得，24m， 24 2p x 当115x时， 1 23.2 10 px，解之得，12x 当1630 x时， 24 23.2p x ，解之得，20 x （3）设每场获得的利润为W（万元） ，则有 当115x时， 2 2 111 402242040 101010 Wxxxxx 所以当15x 时，W最大，最大为 37.5 万元； 当1630 x时， 24960 402224Wx xx 当16x 时，W最大，最大为 36 万元 所以在这 30 次线上销售中，第 15 次线上销售获得利润最大，最大利润 37.5 万元.
