1、2020-2021 学年江苏省常州市八年级（上）期末数学试卷学年江苏省常州市八年级（上）期末数学试卷 一、选择题（本大题共一、选择题（本大题共 8 小题，每小题小题，每小题 2 分，共分，共 16 分）分） 1下面四个手机的图标中，属于轴对称图形的是（ ） A B C D 2下列实数：，0，1.5，2.161161116，其中无理数有（ ） A1 个 B2 个 C3 个 D4 个 3在平面直角坐标系中，点 P（2，3）关于 x 轴对称的点的坐标是（ ） A （2，3） B （2，3） C （2，3） D （2，3） 4下列各组数中，能作为直角三角形的三边长的是（ ） A2，3，4 B6，8，9
2、 C5，12，13 D， 5如图，已知 ACBD，添加下列一个条件后，仍无法判定ABCBAD 的是（ ） AABCBAD BCD90 CCABDBA DCBDA 6若一次函数 ykx+b 的图象经过第一、二、四象限，则（ ） Ak0，b0 Bk0，b0 Ck0，b0 Dk0，b0 7如图，在ABC 中，C90，AD 平分BAC，DEAB，垂足为 E，下列结论：CDED；BD CD；AC+BEAB；SBDE：SACDBD：AC，其中正确的有（ ） A B C D 8周末，小明骑自行车从家里出发去游玩从家出发 1 小时后到达迪诺水镇，游玩一段时间后按原速前往 万达广场小明离家 1 小时 50 分钟
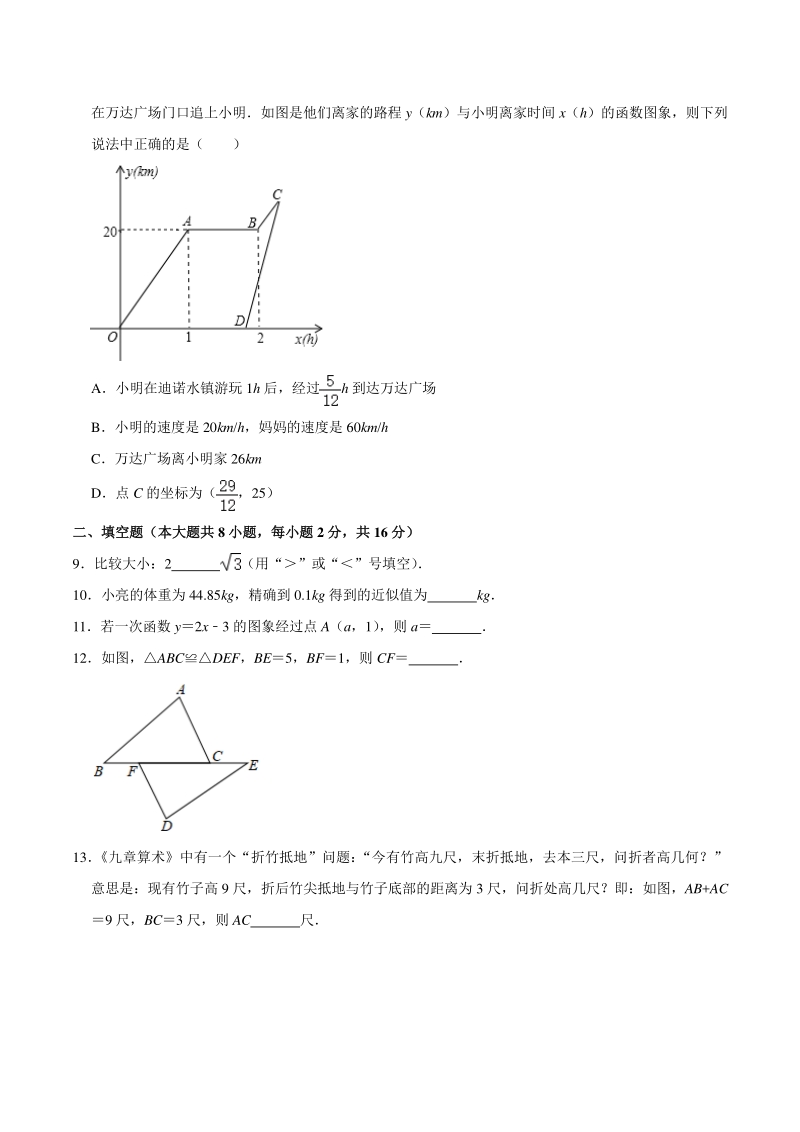
3、后，妈妈驾车沿相同路线前往万达广场妈妈出发 25 分钟时，恰好 在万达广场门口追上小明如图是他们离家的路程 y（km）与小明离家时间 x（h）的函数图象，则下列 说法中正确的是（ ） A小明在迪诺水镇游玩 1h 后，经过h 到达万达广场 B小明的速度是 20km/h，妈妈的速度是 60km/h C万达广场离小明家 26km D点 C 的坐标为（，25） 二、填空题（本大题共二、填空题（本大题共 8 小题，每小题小题，每小题 2 分，共分，共 16 分）分） 9比较大小：2 （用“”或“”号填空） 10小亮的体重为 44.85kg，精确到 0.1kg 得到的近似值为 kg 11若一次函数 y2x
4、3 的图象经过点 A（a，1） ，则 a 12如图，ABCDEF，BE5，BF1，则 CF 13 九章算术中有一个“折竹抵地”问题： “今有竹高九尺，末折抵地，去本三尺，问折者高几何？” 意思是：现有竹子高 9 尺，折后竹尖抵地与竹子底部的距离为 3 尺，问折处高几尺？即：如图，AB+AC 9 尺，BC3 尺，则 AC 尺 14一次函数 y1kx+b 与 y2x+a 的图象如图所示，则不等式 kx+bx+a 的解集为 15在ABC 中，ABAC，BC10，AB 的垂直平分线与 AC 的垂直平分线分别交 BC 于点 D，E，且 DE 4，则 AD+AE 的值为 16如图，RtABC 中，BAC9
5、0，分别以ABC 的三条边为直角边作三个等腰直角三角形：ABD、 ACE、BCF，若图中阴影部分的面积 S16.5，S23.5，S35.5，则 S4 三、解答题（本大题共三、解答题（本大题共 9 小题，共小题，共 68 分。第分。第 17、18 题每题题每题 5 分，第分，第 19 题题 7 分，第分，第 20、21、22、23、24 题每题题每题 8 分，第分，第 25 题题 11 分）分） 17计算： （3.14）0+ 18已知 2（x+1）280，求 x 的值 19已知：如图，ABAE，ABDE，ECB+D180 求证：ABCEAD 20如图，在正方形网格中建立平面直角坐标系，已知ABC
6、 的顶点坐标分别为 A（1，1） 、B（3，4） 、C （4，2） （1）画出ABC； （2）画出ABC 关于 y 轴对称的ABC； （3）若点 P 在 x 轴上，且POA 是等腰三角形，请写出点 P 所有可能的坐标 21如图，一次函数 yx+3 的图象 l1与 x 轴交于点 B，与过点 A（3， 0）的一次函数的图象 l2交于点 C（1， m） （1）求 m 的值； （2）求一次函数图象 l2相应的函数表达式； （3）求ABC 的面积 22如图，ABC 中，AD 是边 BC 上的高，CF 是边 AB 上的中线，DCBF，点 E 是 CF 的中点 （1）求证：DECF； （2）求证：B2BCF
7、 23 某工厂计划每天生产甲、 乙两种型号的口罩共 8000 个， 每生产一个甲种型号的口罩可获得利润 0.5 元， 每生产一个乙种型号的口罩可获得利润 0.3 元设该工厂每天生产甲种型号的口罩 x 个，生产甲、乙两 种型号的口罩每天获得的总利润为 y 元 （1）求 y 与 x 的函数关系式； （2）若每生产 1 个甲种型号的口罩需要 A 原料 2g，每生产 1 个乙种型号的口罩需要 A 原料 1g，受市场 影响，该厂每天能购进的 A 原料至多为 10000g，其他原料充足问：该工厂每天生产甲、乙两种型号的 口罩各多少个时，能获得最大利润？ 24甲骑摩托车从 A 地去 B 地，乙开汽车从 B
8、地去 A 地，两人同时出发，匀速行驶，已知摩托车速度小于 汽车速度，各自到达终点后停止，设甲、乙两人间的距离为 s（km） ，行驶的时间为 t（h） ，s 与 t 之间的 函数关系如图所示，结合图象回答下列问题： （1）甲的速度为 km/h，乙的速度为 km/h； （2）求出图中 a、b 的值； （3）何时两人相距 20km？ 25探究 对于函数 y|x|，当 x0 时，yx；当 x0 时，yx 在平面直角坐标系中画出函数图象，由图象可知，函数 y|x|的最小值是 应用 对于函数 y|x1|+|x+2| 当 x1 时，y ；当 x2 时，y ；当2x1 时，y 在平面直角坐标系中画出函数图象，
9、由图象可知，函数 y|x1|+|x+2|的最小值是 迁移 当 x 时，函数 y|x1|+|2x1|+|3x1|+|8x1|取到最小值 反思 上述问题解决过程中，涉及了一些重要的数学思想或方法，请写出其中一种 2020-2021 学年江苏省常州市八年级（上）期末数学试卷学年江苏省常州市八年级（上）期末数学试卷 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 8 小题）小题） 1下面四个手机的图标中，属于轴对称图形的是（ ） A B C D 【分析】根据轴对称图形的概念判断即可 【解答】解：A、本选项中手机的图标不属于轴对称图形，不符合题意； B、本选项中手机的图标属于轴对称图形，
10、符合题意； C、本选项中手机的图标不属于轴对称图形，不符合题意； D、本选项中手机的图标不属于轴对称图形，不符合题意； 故选：B 2下列实数：，0，1.5，2.161161116，其中无理数有（ ） A1 个 B2 个 C3 个 D4 个 【分析】根据无理数的意义，逐个数进行判断即可 【解答】 解： 无理数是无限不循环小数， 整数和分数都是有理数， 因此无理数有， 2.161161116 共 3 个， 故选：C 3在平面直角坐标系中，点 P（2，3）关于 x 轴对称的点的坐标是（ ） A （2，3） B （2，3） C （2，3） D （2，3） 【分析】直接利用关于 x 轴对称点的性质分析得
11、出答案 【解答】解：点 P（2，3）关于 x 轴对称的点的坐标是： （2，3） 故选：A 4下列各组数中，能作为直角三角形的三边长的是（ ） A2，3，4 B6，8，9 C5，12，13 D， 【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可 【解答】解：A、32+2242，故不是直角三角形，故不符合题意； B、62+8292，故不是直角三角形，故不符合题意； C、52+122132，故是直角三角形，故符合题意； D、 （）2+（）2（）2，故不是直角三角形，故不符合题意 故选：C 5如图，已知 ACBD，添加下列一个条件后，仍无法判定ABCBAD 的是（ ） AABCB
12、AD BCD90 CCABDBA DCBDA 【分析】根据全等三角形的判定方法即可一一判断 【解答】解：在ABC 与BAD 中，ACBD，ABBA， A、SSA 无法判断三角形全等，故本选项符合题意； B、根据 HL 即可判断三角形全等，故本选项不符合题意； C、根据 SAS 即可判断三角形全等，故本选项不符合题意； D、根据 SSS 即可判断三角形全等，故本选项不符合题意； 故选：A 6若一次函数 ykx+b 的图象经过第一、二、四象限，则（ ） Ak0，b0 Bk0，b0 Ck0，b0 Dk0，b0 【分析】根据一次函数的性质和一次函数 ykx+b 的图象经过第一、二、四象限，可以得到 k
13、、b 的正负 情况，从而可以解答本题 【解答】解：一次函数 ykx+b 的图象经过第一、二、四象限， k0，b0， 故选：D 7如图，在ABC 中，C90，AD 平分BAC，DEAB，垂足为 E，下列结论：CDED；BD CD；AC+BEAB；SBDE：SACDBD：AC，其中正确的有（ ） A B C D 【分析】根据角平分线的性质，可得 CDED，易证得ADCADE，可得 AC+BEAB；又由 CD ED，ABD 和ACD 的高相等，所以 SBDE：SACDBE：AC进而可以判断 【解答】解：正确，因为在ABC 中，C90，AD 平分BAC，DEAB 于 E， 所以 CDED； 错误，因为
14、在 RtBDE 中，DBDE，所以 DBCD； 正确，因为由 HL 可知ADCADE，所以 ACAE，即 AC+BEAB； 错误，因为ADCADE， 所以ADE 和ACD 面积相等，高相等都是 DE，所以 SBDE：SACDBE：AC 故选：A 8周末，小明骑自行车从家里出发去游玩从家出发 1 小时后到达迪诺水镇，游玩一段时间后按原速前往 万达广场小明离家 1 小时 50 分钟后，妈妈驾车沿相同路线前往万达广场妈妈出发 25 分钟时，恰好 在万达广场门口追上小明如图是他们离家的路程 y（km）与小明离家时间 x（h）的函数图象，则下列 说法中正确的是（ ） A小明在迪诺水镇游玩 1h 后，经过
15、h 到达万达广场 B小明的速度是 20km/h，妈妈的速度是 60km/h C万达广场离小明家 26km D点 C 的坐标为（，25） 【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题 【解答】解：由图象可得， 小明在迪诺水镇游玩 1h 后，经过（21）h 到达万达广场，故选项 A 错误； 小明的速度为 20120（km/h） ，妈妈的速度是（20+20）60（km/h） ，故选项 B 正确； 万达广场离小明家 20+2020+525（km） ，故选项 C 错误； 点 C 的坐标为（，25） ，故选项 D 错误； 故选：B 二填空题（共二填空题（共 8 小
16、题）小题） 9比较大小：2 （用“”或“”号填空） 【分析】先估算出的值，再根据两正数比较大小的法则进行比较即可 【解答】解：1.732，21.732， 2 故答案为： 10小亮的体重为 44.85kg，精确到 0.1kg 得到的近似值为 44.9 kg 【分析】把百分位上的数字 5 进行四舍五入即可 【解答】解：44.85kg 精确到 0.1kg 得到的近似值为 44.9kg 故答案为 44.9 故答案为 44.9 11若一次函数 y2x3 的图象经过点 A（a，1） ，则 a 2 【分析】将点 A 的坐标代入可求得 a 的值即可 【解答】解：将 A 的坐标（a，1）代入，得：2a31， 解
17、得：a2 故答案为：2 12如图，ABCDEF，BE5，BF1，则 CF 3 【分析】根据题意出去 EF，再根据全等三角形的对应边相等解答即可 【解答】解：BE5，BF1， EFBEBF4， ABCDEF， BCEF3， CFBCBF3， 故答案为：3 13 九章算术中有一个“折竹抵地”问题： “今有竹高九尺，末折抵地，去本三尺，问折者高几何？” 意思是：现有竹子高 9 尺，折后竹尖抵地与竹子底部的距离为 3 尺，问折处高几尺？即：如图，AB+AC 9 尺，BC3 尺，则 AC 4 尺 【分析】竹子折断后刚好构成一直角三角形，设竹子折断处离地面 x 尺，则斜边为（9x）尺，利用勾 股定理解题即
18、可 【解答】解：设竹子折断处离地面 x 尺，则斜边为（9x）尺， 根据勾股定理得：x2+32（9x）2 解得：x4， 答：折断处离地面的高度为 4 尺 故答案为：4 14一次函数 y1kx+b 与 y2x+a 的图象如图所示，则不等式 kx+bx+a 的解集为 x3 【分析】利用函数图象，写出直线 y1kx+b 在直线 y2x+a 下方所对应的自变量的范围即可 【解答】解：根据图象得，当 x3 时，kx+bx+a 故答案为 x3 15在ABC 中，ABAC，BC10，AB 的垂直平分线与 AC 的垂直平分线分别交 BC 于点 D，E，且 DE 4，则 AD+AE 的值为 6 或 14 【分析】
19、根据线段垂直平分线上的点到线段两端点的距离相等可得 ADBD，AECE，然后分两种情况 讨论求解 【解答】解：AB、AC 的垂直平分线分别交 BC 于点 D、E， ADBD，AECE， AD+AEBD+CE， BC10，DE4， 当 BD 与 CE 无重合时，如图 1， AD+AEBD+CEBCDE1046， 当 BD 与 CE 有重合时，如图 2， AD+AEBD+CEBC+DE10+414， 综上所述，AD+AE6 或 14 故答案为：6 或 14 16如图，RtABC 中，BAC90，分别以ABC 的三条边为直角边作三个等腰直角三角形：ABD、 ACE、BCF，若图中阴影部分的面积 S1
20、6.5，S23.5，S35.5，则 S4 2.5 【分析】设 ABBDa，ACCEb，BCEFc，SABGm，SACHn，由 a2+b2c2，可得 SABD+S ACESBCF，由此构建关系式，可得结论 【解答】解：ABD、ACE、BCF 均是等腰直角三角形， ABBD，ACCE，BCEF， 设 ABBDa，ACCEb，BCEFc，SABGm，SACHn， a2+b2c2， SABD+SACESBCF， S1+m+n+S4S2+S3+m+n， S43.5+5.56.52.5 故答案为：2.5 三解答题三解答题 17计算： （3.14）0+ 【分析】直接利用零指数幂的性质以及立方根的性质和二次根
21、式的性质分别化简得出答案 【解答】解：原式132 4 18已知 2（x+1）280，求 x 的值 【分析】根据等式的性质和平方根的意义，将一元二次方程转化为一元一次方程，进而求出答案 【解答】解：2（x+1）280， 移项得，2（x+1）28， 两边都除以 2 得， （x+1）24， 直接开方得，x+12， 即 x+12 或 x+12， 解得 x1 或 x3， 所以 x 的值为 1 或3 19已知：如图，ABAE，ABDE，ECB+D180 求证：ABCEAD 【分析】根据全等三角形的判定方法解答即可 【解答】证明：ABDE， CABE， ECB+D180，ECB+ACB180， DACB，
22、在ABC 与EAD 中， ， ABCEAD（AAS） 20如图，在正方形网格中建立平面直角坐标系，已知ABC 的顶点坐标分别为 A（1，1） 、B（3，4） 、C （4，2） （1）画出ABC； （2）画出ABC 关于 y 轴对称的ABC； （3）若点 P 在 x 轴上，且POA 是等腰三角形，请写出点 P 所有可能的坐标 【分析】 （1）利用点 A、B、C 的坐标描点，从而得到ABC； （2）利用关于 y 轴对称的点的坐标特征写出点 A、B、C的坐标，然后描点即可； （3）先计算出 OA，先以 O 为圆心，OA 为半径画弧交 x 轴于 P1、P2，再作 OA 的垂直平分线交 x 轴于 P3，
23、接着以 A 点为圆心，AO 为半径画弧交 x 轴于 P4，然后写出 P1、P2、P3、P4的坐标即可 【解答】解： （1）如图，ABC 为所作； （2）如图，ABC为所作； （3）OA， 当 O 为顶点时，P 点坐标为（，0）或（，0） ； 当 A 为顶点时，P 点坐标为（2，0） ； 当 P 为顶点时，P 点坐标为（1，0） ， 综上所述，P 点坐标为（，0）或（，0）或（2，0）或（1，0） 21如图，一次函数 yx+3 的图象 l1与 x 轴交于点 B，与过点 A（3， 0）的一次函数的图象 l2交于点 C（1， m） （1）求 m 的值； （2）求一次函数图象 l2相应的函数表达式；
24、（3）求ABC 的面积 【分析】 （1）把点 C（1，m）代入 yx+3 即可求得； （2）根据待定系数法即可求得； （3）求得 B 的坐标，然后根据三角形面积公式求得即可 【解答】解： （1）点 C（1，m）在一次函数 yx+3 的图象上， m1+34； （2）设一次函数图象 l2相应的函数表达式为 ykx+b， 把点 A（3，0） ，C（1，4）代入得， 解得， 一次函数图象 l2相应的函数表达式 y2x+6； （3）一次函数 yx+3 的图象 l1与 x 轴交于点 B， B（3，0） ， A（3，0） ，C（1，4） ， AB6， SABC6412 22如图，ABC 中，AD 是边 BC
25、 上的高，CF 是边 AB 上的中线，DCBF，点 E 是 CF 的中点 （1）求证：DECF； （2）求证：B2BCF 【分析】 （1）连接 DF，根据直角三角形的性质得到 DFABBF，进而证明 DCDF，根据等腰三角 形的三线合一证明结论； （2）根据三角形的外角性质得到FDB2DFC，根据等腰三角形的性质证明结论 【解答】证明： （1）连接 DF， AD 是边 BC 上的高， ADB90， 点 F 是 AB 的中点， DFABBF， DCBF， DCDF， 点 E 是 CF 的中点 DECF； （2）DCDF， DFCDCF， FDBDFC+DCF2DFC， DFBF， FDBB， B
26、2BCF 23 某工厂计划每天生产甲、 乙两种型号的口罩共 8000 个， 每生产一个甲种型号的口罩可获得利润 0.5 元， 每生产一个乙种型号的口罩可获得利润 0.3 元设该工厂每天生产甲种型号的口罩 x 个，生产甲、乙两 种型号的口罩每天获得的总利润为 y 元 （1）求 y 与 x 的函数关系式； （2）若每生产 1 个甲种型号的口罩需要 A 原料 2g，每生产 1 个乙种型号的口罩需要 A 原料 1g，受市场 影响，该厂每天能购进的 A 原料至多为 10000g，其他原料充足问：该工厂每天生产甲、乙两种型号的 口罩各多少个时，能获得最大利润？ 【分析】 （1）根据题意可以写出 y 与 x
27、 的函数关系式； （2）根据该厂每天能购进的 A 原料至多为 10000g，可以求得 x 的取值范围，再根据一次函数的性质， 即可求得该工厂每天生产甲、乙两种型号的口罩各多少个时，能获得最大利润 【解答】解： （1）由题意可得， y0.5x+0.3（8000 x）0.2x+2400， 即 y 与 x 的函数关系式为 y0.2x+2400； （2）由题意可得， 2x+（8000 x）10000， 解得 x2000， y0.2x+2400， y 随 x 的增大而增大， 当 x2000 时，y 取得最大值，此时 y2800，8000 x6000， 答：该工厂每天生产甲、乙两种型号的口罩分别为 200
28、0 个、6000 个时，能获得最大利润 24甲骑摩托车从 A 地去 B 地，乙开汽车从 B 地去 A 地，两人同时出发，匀速行驶，已知摩托车速度小于 汽车速度，各自到达终点后停止，设甲、乙两人间的距离为 s（km） ，行驶的时间为 t（h） ，s 与 t 之间的 函数关系如图所示，结合图象回答下列问题： （1）甲的速度为 40 km/h，乙的速度为 80 km/h； （2）求出图中 a、b 的值； （3）何时两人相距 20km？ 【分析】根据题意结合横纵坐标的意义得出摩托车的速度进而分别分析得出答案 【解答】解： （1）由图象可得：甲骑摩托车的速度为：120340（千米/小时） ， 乙开汽车的
29、速度为（千米/小时） ， 故答案为：40；80； （2）由（1）可知，b120（40+80）1； a401.560； （3）设 x 小时后两人相距 20km，根据题意，得（40+80）x12020 或（40+80）x120+20， 解得 x或 x 答：小时或小时后两人相距 20km 25探究 对于函数 y|x|，当 x0 时，yx；当 x0 时，yx 在平面直角坐标系中画出函数图象，由图象可知，函数 y|x|的最小值是 0 应用 对于函数 y|x1|+|x+2| 当 x1 时，y x ；当 x2 时，y x ；当2x1 时，y x+2 在平面直角坐标系中画出函数图象，由图象可知，函数 y|x1
30、|+|x+2|的最小值是 迁移 当 x 时，函数 y|x1|+|2x1|+|3x1|+|8x1|取到最小值 反思 上述问题解决过程中，涉及了一些重要的数学思想或方法，请写出其中一种 分段去绝对值 【分析】探究画出函数图象，直接得出结论； 应用先去绝对值，得出函数关系式，再画出函数图象，即可得出结论； 迁移分段去绝对值，合并同类项，得出函数关系式，即可得出结论； 反思直接得出结论 【解答】解：探究图象如图 1 所示，函数 y|x|的最小值是 0， 故答案为 0； 应用当 x1 时，yx1+（x+2）x； 当 x2 时，yx+1（x+2）x； 当2x1 时，yx+1+（x+2）x+2； 函数图象如
31、图 2 所示， 由图象可知，函数 y|x1|+|x+2|的最小值是， 故答案为：x，x，x+2，； 迁移 当 x时，yx+12x+13x+14x+15x+16x+17x+18x+136x+8， y， 当x时，yx+12x+13x+14x+15x+16x+17x+1+8x120 x+6， y， 当x时，yx+12x+13x+14x+15x+16x+1+7x1+8x16x+4， 3y， 当x时，yx+12x+13x+14x+15x+1+6x1+7x1+8x16x+2， 3y， 当x时，yx+12x+13x+14x+1+5x1+6x1+7x1+8x116x， y4， 当x时，yx+12x+13x+1+4x1+5x1+6x1+7x1+8x124x2， 4y6， 当x时，yx+12x+1+3x1+4x1+5x1+6x1+7x1+8x130 x4， 6y11， 当x1 时，yx+1+2x1+3x1+4x1+5x1+6x1+7x1+8x134x6， 11y28， 当 x1 时，yx1+2x1+3x1+4x1+5x1+6x1+7x1+8x136x8， y28， 当 x时，函数 y|x1|+|2x1|+|3x1|+|8x1|取到最小值； 反思 用到的数学思想有：数形结合的数学思想，分段去绝对值， 故答案为：分段去绝对值
