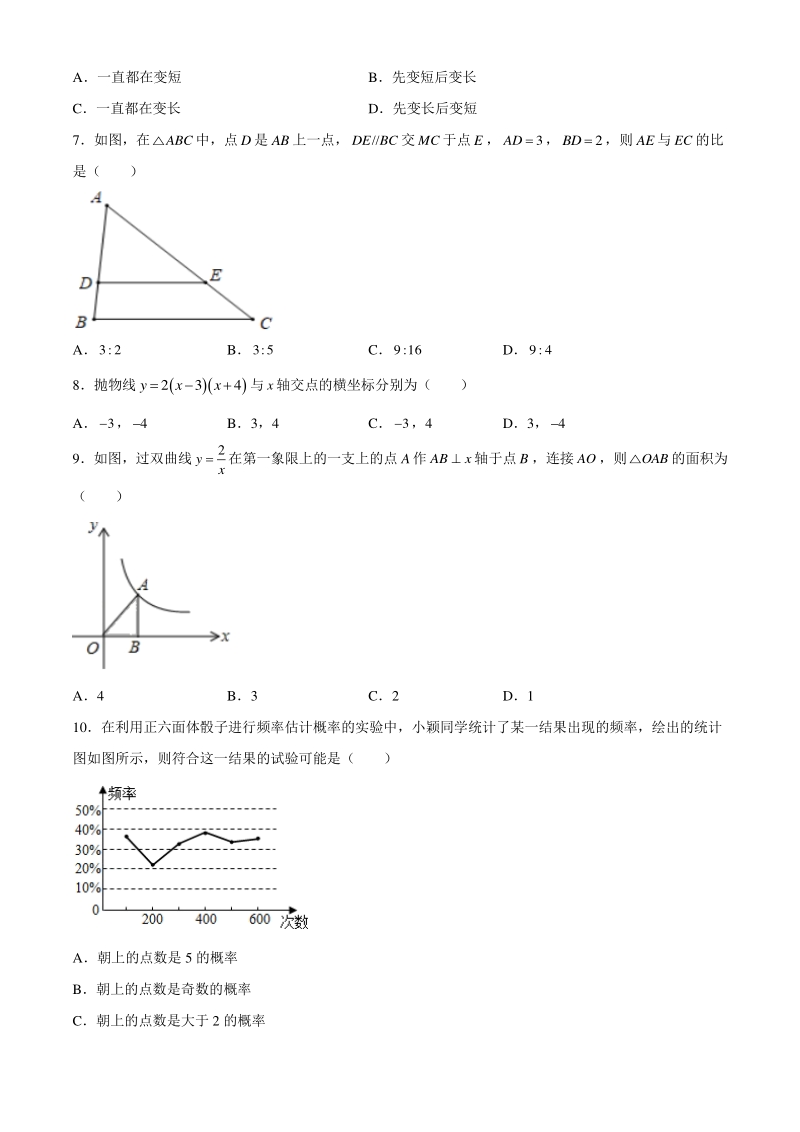
1、20202021 学年度九年级数学上期期末检测试题学年度九年级数学上期期末检测试题 一、选择题（本大题共一、选择题（本大题共 10 个小题，每小题个小题，每小题 3 分，共分，共 30 分，每小题均有四个选项，其中只有一项符合题目分，每小题均有四个选项，其中只有一项符合题目 要求，答案涂在答题卡上）要求，答案涂在答题卡上） 1下列方程是一元二次方程的是（ ） A10 xy B 2 1 2x x C 2 23xx D6xy 2如图是由 6 个相同的小正方体组成的立体图形，这个立体图形的俯视图是（ ） A B C D 3若xm是方程 2 10 xx 的根，则 2 2020mm的值为（ ） A202
2、2 B2021 C2019 D2018 4若 2 234yaxx是二次函数，则a的取值范围是（ ） A2a B0a C2a D0a 5如图，在正方形网格纸中，ABC的三个顶点都在格点上，则tanBAC的值是（ ） A 3 4 B 4 5 C 4 3 D 3 5 6如图，晚上小明在路灯下沿路从A处径直走到B处，这一过程中他在地上的影子（ ） A一直都在变短 B先变短后变长 C一直都在变长 D先变长后变短 7如图，在ABC中，点D是AB上一点，/DE BC交MC于点E，3AD ，2BD ，则AE与EC的比 是（ ） A3:2 B3:5 C9:16 D9:4 8抛物线234yxx与x轴交点的横坐标分
3、别为（ ） A3，4 B3，4 C3，4 D3，4 9如图，过双曲线 2 y x 在第一象限上的一支上的点A作ABx轴于点B，连接AO，则OAB的面积为 （ ） A4 B3 C2 D1 10在利用正六面体骰子进行频率估计概率的实验中，小颖同学统计了某一结果出现的频率，绘出的统计 图如图所示，则符合这一结果的试验可能是（ ） A朝上的点数是 5 的概率 B朝上的点数是奇数的概率 C朝上的点数是大于 2 的概率 D朝上的点数是 3 的倍数的概率 二、填空题（本大题共二、填空题（本大题共 4 个小题，每小题个小题，每小题 4 分，共分，共 16 分，答案写在答题卡上）分，答案写在答题卡上） 11若
4、1 5 a b ，则 a ab 的值为_ 12反比例函 3m y x 数，在每一象限内，y随x的增大而减小，则m的取值范围_ 13如图，OAB与是DOC以点O为位似中心的位似图形，相似比为1:2，若点B的坐标为2,1，则 点C的坐标为_ 14如图，桥洞的拱形是抛物线，当水面宽AB为12m时，桥洞顶部离水面4m若选取拱形顶点C为坐标 原点，以水平方向为x轴，建立平面直角坐标系，此时该抛物线解析式为_ 三、解答题（本大题共三、解答题（本大题共 6 个小题，共个小题，共 54 分，解答过程写在答题卡上）分，解答过程写在答题卡上） 15 （1）计算：2382sin602cos45 （2）解方程： 2
5、120 xx 16已知关于x的一元二次方程有 2 1210axx 两个不相等的实数根，a的取值范围是 17如图，航拍无人机在C处测得正前方某建筑物顶部处A的仰角为 45，测得底部B的俯角为 31此 时航拍无人机距地面CD的高度为 12 米， 求该建筑物的高度AB（结果保留整数） （参考数据：tan310.60 ） 18对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境为了检查垃圾分类的 落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的A，B，C，D四个 小区进行检查，并且每个小区不重复检查 （1）甲组抽到A小区的概率是 ； （2）请用列表或画树状图的
6、方法求甲组抽到A小区，同时乙组抽到C小区的概率 19如图，直线yxb与双曲线0 k yk x 交于A、B两点，且点A的坐标为2,3 （1）求双曲线与直线的解析式； （2）求点B的坐标； （3）若 k xb x ，直接写出x的取值范围 20如图，矩形ABCD的对角线AC、BD相交于点F，延长BC到点E，使CEBC，连接DE，连接AE 交BD于点G，交CD于点H （1）求证：四边形ACED是平行四边形； （2）求证： 2 DGFG BG； （3）若10AB ，12BC ，求线段GH的长度 四、填空题（本大题共四、填空题（本大题共 5 分，每小题分，每小题 4 分，共分，共 20 分，答案写在答题卡
7、上）分，答案写在答题卡上） 21在比例尺1:200000是的地图上，A、B两地间的距离为4cm若还是用cm单位，则A、B两地的实 际距离用科学记数法表示应为_ 22 在长度分别为 3、 4、 7、 9 的四条线段中， 任意选取三条， 端点顺次连接， 能组成三角形的概率为_ 23设a，b分别是方程 2 20220 xx的两个实数根，则 2 2aab的值是_ 24 如图， 点C在线段AB上， 等腰ADC的顶角120ADC， 点M是矩形CDEF的对角线DF的中点， 连接MB，若6 3AB ，6AC ，则MB的最小值为为_ 25如图，每个台阶的高和宽分别是 1 和 2，台阶凸出的角的顶点记作 m T（
8、其中m为 18 的整数） ，函数 1 0ykxx 的图象为曲线L若曲线L使得 18 TT这些点分布在它的两侧，每侧各 4 个点，则k的取值 范围为_ 五、解答题（本大题共五、解答题（本大题共 3 个小题，共个小题，共 30 分，解答过程写在答题卡上）分，解答过程写在答题卡上） 26某商场销售一批名牌衬衫：平均每天可售出 20 件，每件盈利 40 元，为了扩大销售量，增加盈利，尽 快减少库存，商场决定采取适当的降价促销措施，经市场调查发现：如果每件衬衫降价 1 元，那么平均每 天就可多售出 2 件 （1）求出商场盈利与每件衬衫降价之间的函数关系式； （2）若每天盈利达 1200 元，那么每件衬衫
9、应降价多少元？ 27 如图， 以ABC的两边AB、AC分别向外作等边ABD和等边ACE，BE与CD交于点P， 已知3PA ， 4PB ，5PC （1）求证：ADCABE； （2）求DPB的度数及BE的长； （3）若点Q、R分别是等边ABD和等边ACE的重心（三边中线的交点） ，连接AQ、AR、QR，作 出图象，求QR的长 28如图，在平面直角坐标系xOy中，已知抛物线 2 yaxbxc与x轴交于3,0A ，1,0B两点，与y轴 交于点0,3C，连接AC，点P为第二象限抛物线上的动点 （1）求a、b、c的值； （2）连接PA、PC、AC，求PAC面积的最大值； （3）过P作PQAC，垂足为Q，是
10、否存在这样的点P、Q，使得CPQCBO，若存在，请求出所 有符合条件的点P的坐标；若不存在，请说明理由 九年级数学参考答案及评分建议九年级数学参考答案及评分建议 A 卷（卷（100 分）分） 一一、选择题（本大题共十小题，每小题选择题（本大题共十小题，每小题 3 分，共分，共 30 分）分） 1-5 CDBAC 6-10 BADDC 二、填空题（本大题共四小题，每小题二、填空题（本大题共四小题，每小题 4 分，共分，共 16 分）分） 11 1 6 123k 134, 2 14 2 1 9 yx 三三、解答题解答题（本大题共六小题，共（本大题共六小题，共 54 分）分） 15 解： （1）原式
11、 32 232 222 22 22 （2）340 xx 30 x 或40 x 1 3x ， 2 4x 方法 2： 2 14 112490 149 2 1 x 1 3x ， 2 4x 16 解：原方程是一元二次方程，10k ，解得1k ； 方程 2 1210kxx 有两个不相等的实数根， 2 24110k ，解得2k ； 使原方程有两个不相等的实数根，k的取值范围为2k 且1k 17 解：如图，由矩形BDCE可知，12BECD米； 在RtBCE中，tan BE BCE CE ，31BCE， 12 0.60 CE ， 20CE 米 在RtACE中，45ACE， 20AECE米； 32ABBEAE米
12、 18 解： （1）共有A、B、C、D，4 个小区， 甲组抽到A小区的概率是 1 4 ； （2）用列表法表示所有可能出现的情况： 总共有：AB、AC、AD、BA、BA、BC、BD、CA、CB、CD、DA、DB、DC，共 12 种等可能的 结果数， 其中甲组抽到A小区，同时乙组抽到C小区的结果数为 1， 甲组抽到A小区，同时乙组抽到C小区的概率为 1 12 19 解： （1）点2,3A在双曲线 k y x 上，也在直线yxb上 326k ，321b ； 双曲线的解析式为 6 y x ， 直线的解析式为1yx； （2）点B是直线1yx和双曲线 2 y x 的交点， 点B的坐标是方程组 1 2 yx
13、 y x 的一个解； 1 1 2 3 x y ， 2 2 3 2 x y ； 点B的坐标为3, 2 ； （3）30 x 或2x ； 20 （1）证明：矩形ABCD，/AD BC，ADBC， 延长BC到点E，使CEBC，/AD CE，ADCE， 四边形ACED是平行四边形； （2）证明：/AD BE， ADGEBG， DGAG BGGE ， 四边形ACED是平行四边形，/AC DE， AGFEGD， AGFG GEDG ， DGFG BGDG ， 2 DGFG BG； （3）四边形ACED为平行四边形，AE，CD相交点H， 1 5 2 DHDCAB，12ADCE， 在RtADH中， 222 16
14、9AHADDH 13AH ， 在RtABE中， 222 676AEABBE 26AE ， ADGBGE， 1 2 AGAD GEBE ， 1 2 AGGE，2GEAG， 126 33 AGAE， 2613 13 33 GHAHAG B 卷（卷（50 分）分） 一一、填空题填空题（本大题共五小题，每小题（本大题共五小题，每小题 4 分，共分，共 20 分）分） 21 5 8 10 cm 22 1 2 232021 2492 3 253628k 二二、解答题解答题（本大题共三小题，共（本大题共三小题，共 30 分）分） 26 解： （1）设每件降低x元，获得的总利润为y元，则 2 40202260
15、800yxxxx ； （2）当1200y 时，即 2 2608001200 xx， 1 10 x ， 2 20 x ， 需尽快减少库存， 每件应降低 20 元时，商场每天盈利 1200 元 27 解： （1）ABD和ACE都为等边三角形， ADAB，AEAC， 60DABEACAECAEC ， DABBACEACBAC ， 即DACBAE ， ADCABE SAS； （2）ADCABE， ADPABP， AODPOB ， 60DPBDAB ； 在PE上取点F，使60PCF， 设AB，PD交于O， 同（1）可得APCEFC， 60EPCEAC ， 3EFAP，CPF为等边三角形， 45312BE
16、PBPFFE； （3）过点Q作QGAD于G，设QGx， 点Q、R分别是等边ABD和等边ACE的重心， 2AQx，3AGx，2 3ADx， 3 3 AQAR ABAE QARQABBACRAC 3030BAC 60BAC ， QARBAE， ABEAQR， QRAQ BEAB ， 3 124 3 3 QR 28 解： （1）设抛物线的解析式为13ya xx 将0,3C代入得：33a，解得1a ， 抛物线的解析式为13yxx，即 2 23yxx， 1a ，2b ，3c ； （2）过点P作PEx轴，交AC于点P，设点P的横坐标为m， 点P在抛物线 2 23yxx上， 2 ,23P mmm 直线AC过
17、点3,0A 、点0,3C， 直线AC解析式可求得为：3yx， ,3E m m 22 2333PEmmmmm 2 13 3 22 PACPAEPCE SSSPE OAmm 2 2 33327 3 2228 PAC Smmm 当点P的横坐标为 3 2 时，PAC面积的最大值为 27 8 ； 方法 2：切线，平行于AC的直线，参照给分； （3）假设存在，过点Q作x轴的平行线l，过点P、C作l的垂线，垂足为MN， CPQCBO， 1 3 PQOB CQOC 可证：PMQQNC AA； 1 3 PMMQPQ QNCNCQ 设 2 ,23P mmm，,3Q n n， 2 2PMmmn ，MQnm，QNn ，CNn ， 2 32nmmn ，3nnm ， 5 2 m ， ，存在， 5 7 , 2 4 P
