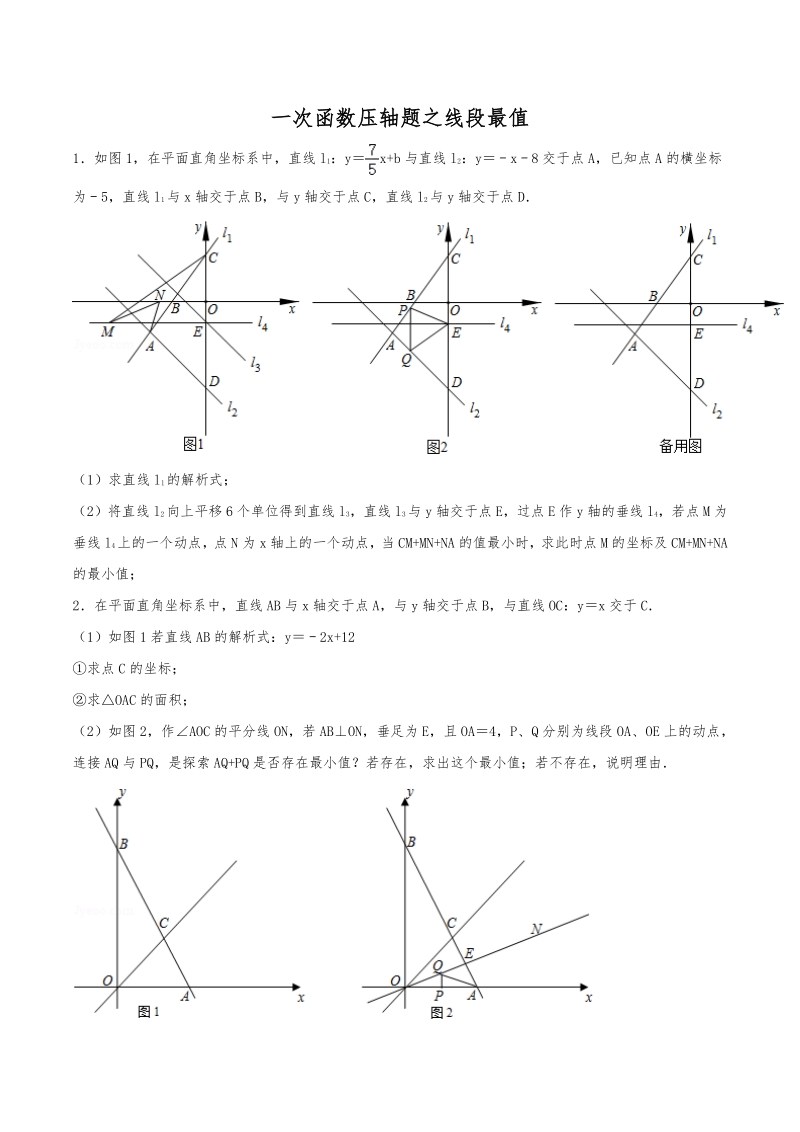
1、一次函数压轴题之线段最值一次函数压轴题之线段最值 1如图 1，在平面直角坐标系中，直线 l1：yx+b 与直线 l2：yx8 交于点 A，已知点 A 的横坐标 为5，直线 l1与 x 轴交于点 B，与 y 轴交于点 C，直线 l2与 y 轴交于点 D （1）求直线 l1的解析式； （2）将直线 l2向上平移 6 个单位得到直线 l3，直线 l3与 y 轴交于点 E，过点 E 作 y 轴的垂线 l4，若点 M 为 垂线 l4上的一个动点，点 N 为 x 轴上的一个动点，当 CM+MN+NA 的值最小时，求此时点 M 的坐标及 CM+MN+NA 的最小值； 2在平面直角坐标系中，直线 AB 与 x
2、 轴交于点 A，与 y 轴交于点 B，与直线 OC：yx 交于 C （1）如图 1 若直线 AB 的解析式：y2x+12 求点 C 的坐标； 求OAC 的面积； （2）如图 2，作AOC 的平分线 ON，若 ABON，垂足为 E，且 OA4，P、Q 分别为线段 OA、OE 上的动点， 连接 AQ 与 PQ，是探索 AQ+PQ 是否存在最小值？若存在，求出这个最小值；若不存在，说明理由 3如图，在平面直角坐标系中，矩形 OABC 的顶点 A（4，0） ，C（0，3） ，直线 yx+交 OA 于点 D， 交 BC 于点 E，动点 P 从点 O 出发，以每秒 2 个单位长度的速度沿 OAAB 运动，
3、到点 B 停止，设PDE 的面 积为 S（平方单位） ，点 P 的运动时间为 t（秒） （1）求点 D 和点 E 的坐标； （2）求 S 与 t 之间的函数关系式，并写出 t 的取值范围； （3）当点 P 在边 AB 上运动，且 PD+PE 的值最小时，直接写出直线 EP 的表达式 4一次函数的图象与 x 轴、y 轴分别交于点 A（8，0）和点 B（0，6） （1）确定此一次函数的解析式 （2）求坐标原点 O 到直线 AB 的距离 （3） 点 P 是线段 AB 上的一个动点， 过点 P 作 PM 垂直于 x 轴于 M， 作 PN 垂直于 y 轴于 N， 记 LPM+PN， S=PM PN 问
4、L 和 S 是否存在最大值和最小值？若存在，求出此时 P 点到原点 O 的距离，若不存在请说明理由 5如图，在平面真角坐标系中，点 A 的坐标是（，0） ，点 B 的坐标是（0，1） 点 B 和点 C 关于原点 对称点 P 是直线 AB 位于 y 轴右侧部分图象上一点，连接 CP，已知 SBPCSABC， （1）求直线 AC 的解析式； （2）如图 2，AOC 沿着直线 AC 平移得AOC，平移后的点 A与点 C 重合点 F 为直线 AC 上的一动 点， 当 PF+FC的值最小时，请求出 PF+FC的最小值及此时点 F 的坐标； （3）如图 3，将PBC 沿直线 PA 翻折得PBG，点 N 为
5、平面内任意一动点，在直线 PA 上是否存在点 M，使 得以点 M、N、P、G 为顶点的四边形是矩形？若存在，请直接写出点 M 的坐标；若不存在，说明理由 6如图，在平面直角坐标系中，平行四边形 ABCD 的边 AB 在 x 轴上，AD 与 y 轴交于点 E，连接 BE，已知点 A（3，0） 、B（3，0） 、C（7，4） ，点 G 为对角线 BD 上一点，过点 G 作 y 轴的平行线交 BE 于点 F，点 M、 N 是直线 BE 上的两个动点（点 M 在点 N 的上方） ，且 MN，连接 GN、DM （1）求BDE 的面积； （2）若 GF，求 DM+MN+NG 的最小值，此时在 y 轴上有一
6、动点 R，当|GRNR|最大时，求点 R 的坐标； （3）在（2）的条件下，把GFB 绕点 B 逆时针旋转一个角 a（0180） ，在旋转过程中，直线 GF 与直线 BE、x 轴分别交于点 P、点 Q，当BPQ 是以 B 为顶点的等腰三角形时，求出 PQ 的长以及相应的旋转 角的度数 7如图，直线 ykx+b 与 x 轴和 y 轴交于 A、B 两点，AB4，BAO45 （1）如图 1，求直线 AB 的解析式 （2）如图 1，直线 y2x2 交 x 轴于点 E且 P 为该直线在直线 AB 上方一动点，当PAB 的面积等于 10 时，将线段 PE 沿着 x 轴平移得到线段 P1E1，连接 OP1求
7、 OP1+P1E1+的最小值 （3）如图 2，在（2）问的条件下，若直线 y2x2 与 y 轴的交点是 C，连接 CE1，得到OCE1，将OCE1 绕着原点 O 逆时针旋转（0180） ，旋转过程中直线 OC 与直线 AB 交于点 M，直线 CE1与直线 AB 交 于点 N，当CMN 为等腰三角形时，直接写出的值 8如图，在平面直角坐标系中，直线 yx+4 分别交 x 轴，y 轴于 A，B 两点，点 C 为 OB 的中点，点 D 在 第二象限，且四边形 AOCD 为矩形（有一个角是直角的平行四边形） （1）直接写出点 A，B 的坐标，并求直线 AB 与 CD 交点 E 的坐标； （2）动点 P
8、 从点 C 出发，沿线段 CD 以每秒 1 个单位长度的速度向终点 D 运动；同时动点 N 从点 A 出发， 沿线段 AO 以每秒 1 个单位长度的速度向终点 O 运动，过点 P 作 PHOA，垂足为 H，连接 NP设点 P 的运动 时间为 t 秒 若NPH 的面积为 1，求 t 的值； 点Q是点B关于点A的对称点， 问BP+PH+HQ是否有最小值？如果有， 直接写出相应的点P的坐标和BP+PH+HQ 的最小值；如果没有，请说明理由 9已知直线 yx+6 与 x 轴，y 轴分别相交于点 A，B，将OBA 对折，使点 O 的对应点 E 落在直线 AB 上，折痕交 x 轴于点 C （1）求点 C
9、的坐标和直线 BC 的函数表达式； （2）若已知 x 轴上有一点 D（4，0） ，点 M 为直线 AB 上一点，点 N 为直线 BC 上一点，是否存在这样的点 M、 N，使得以点 A、D、M、N 为顶点的四边形是平行四边形？若存在，求出点 M 的坐标：若不存在，说明理由； （3）已知 y 轴上有点 P（0，2） ，点 Q 为直线 BC 上一点，点 K 为直线 yx 上一点，是否存在合适的点 Q， K，使得 PQ+KQ 最小？若存在，求出 PQ+KQ 的最小值以及此时 K 点的坐标；若不存在，请说明理由 10在平面直角坐标系 xoy 中，直线 yx+m（m0）与 x 轴，y 轴分别交于 A，B
10、两点，点 P 在直线 AB 上 （1）如图 1，若 m+1，点 P 在线段 AB 上，POA60，求点 P 的坐标； （2）如图 2，以 OP 为对角线作正方形 OCPD（O，C，P，D 按顺时针方向排列） ，当点 P 在直线 AB 上运动时， 的值是否会发生变化？若不变，请求出其值；若变化，请说明理由； （3）如图 3，在（1）的条件下，Q 为 y 轴上一动点，连 AQ，以 AQ 为边作正方形 AQEF（A，Q，E，F 按顺时 针方向排列） ，连接 OE，AE，则 OE+AE 的最小值为 11如图，一次函数 ykx+b 的图象与 x 轴交于点 A，与 y 轴交于点 B（0，2） ，与正比例函
11、数 yx 的图 象交于点 C（4，c） （1）求 k 和 b 的值； （2）如图 1，点 P 是 y 轴上一个动点，当|PAPC|最大时，求点 P 的坐标； （3）如图 2，设动点 D，E 都在 x 轴上运动，且 DE2，分别连结 BD，CE，当四边形 BDEC 的周长取最小值 时直接写出点 D 和 E 的坐标 12如图 1，在平面直角坐标系中，直线 l：y与 x 轴交于点 A，且经过点 B（2，m） ，已知点 C（3， 0） （1）求直线 BC 的函数解析式； （2）在线段 BC 上找一点 D，使得ABO 与ABD 的面积相等，求出点 D 的坐标； （3）y 轴上有一动点 P，直线 BC 上
12、有一动点 M，若APM 是以线段 AM 为斜边的等腰直角三角形，求出点 M 的坐标； （4）如图 2，E 为线段 AC 上一点，连结 BE，一动点 F 从点 B 出发，沿线段 BE 以每秒 1 个单位运动到点 E 再沿线段 EA 以每秒个单位运动到 A 后停止，设点 F 在整个运动过程中所用时间为 t，求 t 的最小值 1 【解答】解： （1）点 A 的横坐标为5， A（5，3） ， 将点 A 代入 yx+b， b4， 直线 l1的解析式 yx+4； （2）l2：yx8 与 y 轴的交点 D（0，8） ， 将直线 l2向上平移 6 个单位得到直线 l3，直线 l3与 y 轴交于点 E， E（0
13、，2） ， 过点 E 作 y 轴的垂线 l4， 点 D 是点 C 关于直线 l4的对称点，作点 A 关于 x 轴的对称点 A（5，3） ， 连接 AD交 x 轴、l4于点 N、M，则此时 CM+MN+NA 最小，最小值为：AD， CM+MN+NAMD+MN+ANAD， AD； CM+MN+NA 的值最小为； 2 【解答】解： （1）联立 AB、OC 的函数表达式得：， 点 C（4，4） ； 直线 AB 的解析式：y2x+12 令 y0，则 x6，即 OA6， SOACOAyC6412； （2）ON 是AOC 的平分线，且 ABON， 则点 A 关于 ON 的对称点为点 C，AOOC4， 当 C
14、、Q、P 在同一直线上，且垂直于 x 轴时，AQ+PQ 有最小值 CP， 设：CPOPx，则 2x 24216， 解得：x2CP 3 【解答】解： （1）yx+，当 y0 时，x3，即点 D（3，0） ， 当 y3 时，x1，故点 E（1，3） ， 故：D（3，0） ，E（1，3） ； （2）如图 1，当点 P 在 OD 段时，此时 0t， SPDOC3t+； 当点 P 在 DA 段时，此时t2， 同理可得：S3t； 当点 P（P）在 AB 段时，此时 2t， SS梯形 DABESADPSBEP61（2t4）3（72t）2t； 故 S时 2t； （3）在 x 轴上取点 D 的对称点 D（5，0
15、） ，连接 DE 交 AB 于点 P，则此时 PD+PE 的值最小， 将点 E、D的坐标代入一次函数表达式：ykx+b 得：，解得：， 故直线 EP 的表达式为：yx+ 4 【解答】解： （1）设一次函数解析式为 ykx+b， 函数图象经过点 A（8，0）和点 B（0，6） ， ， 解得 所以，函数解析式为 yx+6； （2）设点 O 到 AB 的距离为 h， 点 A（8，0）和点 B（0，6） ， OA8，OB6， 由勾股定理得，AB10， SAOB10h86， 解得 h4.8， 所以，坐标原点 O 到直线 AB 的距离为 4.8； （3）设 AMx， 则 OMOAAM8x， PMx 轴，P
16、Ny 轴， 四边形 OMPN 是矩形， PNOM8x， PMAM tanBAOxx， LPM+PNx+8xx+8， 点 P 是线段 AB 上的一个动点， 点 M 在线段 OA 上， 0 x8， 0， 当 x0 时，L 值最大，最大值为 8，此时，点 P 到原点 O 的距离为 8， x8 时，L 值最小，最小值为 6，此时，点 P 到原点 O 的距离为 6 5 【解答】解： （1）点 B 和点 C 关于原点对称，则点 C（0，1） ， 将点 A、C 的坐标代入一次函数表达式：ymx+n 得：，解得：， 故直线 AC 的表达式为：yx1； （2）过点 C作直线 lx 轴，过点 P 作 PFl，垂足
17、为点 F，交 AC 于点 F， tanABO，故ABO60，BAO30， OAB30FCF，FFFC， 则 PF+FCPF+FFPF，即此时，PF+FC最小，最小值为 PF， SBPCSABC，则|xP|xA|， 故点 P（，） ， ACCC2，则点 C（，2） ， 则点 F（，2） ， 点 F（，） ， PF+FC最小值 PF； （3）存在，理由： 当 GMPM 时， 如图ABC60ABG， GBH60，GBBC2， 则 GHGBsinGBH2sin60， 故点 G（，2） ； M、N、P、G 为顶点的四边形是矩形， 点 M 位置如下图所示，设点 M（m，m+1） ， 将点 A、B 的坐标代
18、入一次函数：ysx+t 得：，解得：， 故直线 AB 的表达式为：yx+1， GMAB，则设直线 GM 的表达式为：yx+b， 将点 G 的坐标代入上式得：2（）+b，解得：b1， 故：直线 GM 的表达式为：yx1， 联立并解得：x， 故点 M（，） ； 当 GMGP 时， 同理可得：点 M（，） ； 综上，点 M（，）或（，） 6 【解答】解： （1）四边形 ABCD 是平行四边形， CDAB，CDAB6 C（7，4） D（1，4） 设直线 AD 解析式为 ykx+b，将 A（3，0） ，D（1，4）代入得，解得， 直线 AD 解析式为 yx+3，令 x0，得 y3， E（0，3） SBD
19、ESABDSABE64633 （2）设直线 BE 解析式为 yk1x+b1，将 B（3，0） 、E（0，3）代入得，解得， 设直线 BE 解析式为 yx+3， 设直线 BD 解析式为 yk2x+b2，将 B（3，0） 、D（1，4）代入得，解得， 设直线 BD 解析式为 y2x+6， 设 G（m，2m+6） ，F（m，m+3） ，由题意得 GF2m+6（m+3）m+3，解得 m， G（，3） ，F（，） ； 如图 1，OBOE3 OBE45 OEOBBE MN， 点 M 分别向右向下平移个单位得到点 N， 作点 D 关于直线 BE 得对称点 D1，连接 D1M，过点 N 作 D2ND1M 且
20、D2ND1M， D1（1，2） ，D2（，） ， DM+MN+NGMN+D2N N+GN， 当 D2、N、G 在同一直线上时，D2N N+GND2G 为最小值， D2G， DM+MN+NG 的最小值为 当点 R、N、G 在同一直线上时，|GRNR|最大， 点 R 是直线 D2G 与 y 轴的交点 设直线 D2G 解析式为 yk3x+b3，将 D2（，） ，G（，3） ，代入得，解得， 直线 D2G 解析式为 yx+，令 x0，得 y R（0，） （3）BPQ 为等腰三角形，PBQ45或 135， BQP22.5或 45或 67.5或 90 BFG 中，BFG180GFE18045135，BFB
21、E 在旋转过程中，直线 GF 与 x 轴的交点 Q 在点 B 左侧时，BQP90，BPQ 不可能为等腰三角形 当点 Q 在点 B 右侧时，分三种情况： 如图 2，BQPPBQ45， BPQ90 BFGBFG135 BFQ18013545， FBQ90， FBFOBE+OBF45+90135，即旋转角135； 在BFQ 中，FBQ90，BFQBQF45， BQBF， PBQOBE45， BPQ180PBQBQF90， PQBQ sinPBQsin45（舍去） ； 如图 3，BQPBPQ67.5，BFG135， BFQ45， FBQ180BFQBQP1804567.567.5， OBF180FBQ
22、18067.5112.5 旋转角OBE+OBF45+112.5157.5 过点 B 作 BMPQ 于 M，FBQBQP67.5， FQFB， 在 RtFBM 中，BFM45， BMFMBF，MQFQFM， BPQBQP， BPBQ BMPQ PQ2MQ2（）33 如图 4，BQPBPQ22.5时，BFG135， BFP45， FBQBFPBQP4522.522.5 旋转角EBO+FBQ45+22.567.5； 过点 B 作 BMPQ 于 M，BQPBPQ22.5， BPBQ BMPQ PQ2MQ FBQBQP， FQBF， BFP45， FMBFcosBFPcos45 PQ2MQ2（+）3+3
23、 BQP90时， 旋转角180，0180 不符合题意 综上所述，PQ3+3，67.5或 PQ33，157.5 7 【解答】解： （1）由 k0， BAO45， BOAO AB4， A（4，0） ，B（0，4） ， yx4， （2）如图 1： P 为直线 y2x2 在直线 AB 上方一动点， 设点 P（m，2m2） ，点 P 在直线 AB 上方，且PAB 的面积等于 10， OAB 的面积等于 8，点 P 位于 x 轴上方 由 S梯形 APFO+SAOBSPBFSPAB得 10 解得 m3； P（3，4） ； E（1，0） ， PEP1E12， 作 P1关于 y 轴的对称点 P2，过 E1作 E
24、1DAB 于 D，过 P2作 P2Gx 轴于 G，连接 OP2，过点 E1作 E1P3OP2，且 使 E1P3OP2，此时 P3、E1、D 成一直线时，E1P3+DE1的值最小，即 OP2+DE1的值最小， 此时，OP1+P1E1+最小 OP2DE1， AE1D45 DE1O135 P2OA135， P2OG45 点 P2的横坐标与纵坐标互为相反数，点 P1的横、纵坐标相等， P1（4，4） ，E1（2，0） ， OP2OP1，DE1AE， OP1+P1E1+最小就是求 OP2+DE1， 当 OP2DE1时，OP2+DE1的值最小， P2OGAE1D45， OP1OP2P2G4 P2（4，4）
25、 ，P1（4，4） ，E1（2，0） ， AE1OAOE1422， OP1+P1E1+的最小值为 5+2 （3）由题意得：C（0，2） ，OCOE1，COE190， CMN 为等腰三角形，分四种情况： CNMNCM45（如图 2） ，旋转角45； CNMCMN67.5（如图 3） ，旋转角67.5； CMNNCM45（如图 4） ，旋转角90； CMNNCM22.5（如图 5） ，旋转角157.5 综上所述，旋转角45，67.5，90，157.5时，CMN 是等腰三角形 8 【解答】解： （1）A 是直线 yx+4 与 x 轴的交点， 令 y0 得 x3 A（3，0） 又B 是直线 yx+4
26、与 y 轴的交点， 令 x0，解得 y4 B（0，4） 由题意知，点 C 为 OB 的中点，且四边形 AOCD 为矩形 直线 CD 的方程为 y2 直线 AB 与 CD 交点为 E， 联立，解得 E（1.5，2） （2）分两种情况讨论： 第一种情况当 0t1.5 时，如图 1， 根据题意可知：经过 t 秒，CPt，ANt，HOCPt，PHOC2， NH32t， S NPHPH NH，且NPH 的面积为 1， 2（32t）1， 解得：t1； 第二种情况：当 1.5t3 时，如图 2， 根据题意可知：经过 t 秒，CPt，ANt，HOCPt，PHOC2， AH3t， HNANAHt（3t）2t3，
27、 S NPHPH NH，且NPH 的面积为 1， 2（2t3）1 解得：t2； 当 t1 或 2 时，存在NPH 的面积为 1； BP+PH+HQ 有最小值，最小值为 如图 3，连接 PB、CH，则四边形 PBCH 是平行四边形， BPCH BP+PH+HQCH+HQ+2 要使 CH+HQ 的值最小，只须 C、H、Q 三点共线即可， 点 Q 是点 B 关于点 A 的对称点， Q（6，4） 又点 C（0，2） 直线 CQ 的解析式为：yx+2 令 y0，得 x2， H（2，0） ， 所求点 P 的坐标为 P（2，2） 根据勾股定理可得 CQ 此时，BP+PH+HQCH+HQ+PHCQ+2 9 【
28、解答】解： （1）连接 CE，则 CEAB， yx+6 与 x 轴，y 轴分别相交于点 A，B， 则点 A、B 的坐标分别为： （8，0） 、 （0，6） ，则 AB10， 设：OCa，则 CEa，BEOB6， AE1064，CA8a， 由勾股定理得：CA 2CE2+AE2，即（8a）2a2+42， 解得 a3， 故点 C（3，0） ； 将点 B、C 的坐标代入一次函数表达式：ykx+b 并解得： 直线 BC 的表达式为：y2x+6； （2）AD4，设点 M（m，m+6） ，点 N（n，2n+6） ， 当 AD 是平行四边形的边时， 则 MNAD，且 MNAD， 即：m+62n+6，mn4，
29、解得：m， 故点 M（，）或（，） ； 当 AD 是平行四边形的对角线时， 由中点公式可得： m+n6+6，m+62n+60， 解得：m， 故点 M（，） ； 综上，点 M（，）或（，）或（，） ； （3）在 BA 上取 BPBP，则点 P是点 P 关于直线 BC 的对称点， 过点 P作 PK直线 yx 交于点 K，交 BC 于点 Q，则 PQ+KQ 为最小，最小值为 PK， 点 P（0，2） ，设BAO， 则 tan，则 cos，PB624， xPPBcos4， 故点 P（，） ， PK直线 yx，则直线 PK 的表达式为：yx+s， 将点 P的坐标代入上式并解得：s， 故直线 BP的表达式
30、为：yx+， 将上式与 yx 联立并解得：x， 故点 K（，） ， PQ+KQ 为最小值 PK 为： 10 【解答】解： （1）如图 1 所示：过点 P 作 PGOA，垂足为 G yx+m， A（m，0） ，B（0，m） OBOAm+1 PAG45 又PGA90， PGGA POG60，PGO90 PGOG （+1）OG+1 OG1， PG 点 P 的坐标为（1，） （2）的值不变 如图 2 所示，过点 O 作 OMOP 交 PC 的延长线与 M，连接 BM 四边形 OCPD 是正方形， OCPC，OCP90， OPC45 MOP90， OMPOPM45， OPOM A（m，0） 、B（0，m
31、） ， OAOBm BOAMOP90， POAMOB OAOB，POAMOB，OPOM， POAMOB（SAS） ， OAPOBM135， MBP90， C 为 PM 的中点， BCCPOP， （3）如图 3 所示：过 E 作 EK 垂直 y 轴与 K，设 Q（0，a） 可证明OAQKQE OQKEa，AOKQ+1 E（a，a+1） 点 E 在直线 yx+1 上运动， 点 B 在直线 yx+1 上 设直线 yx+1 交 x 轴与 N N（1，0） BNO45 作点 O 关于直线 yx+1 的对称点 O1，连接 AO1，交直线 yx+1 与 E1，连接 OE1、O1N、O1E OE1O1E1 O
32、E1+AE1O1AO1E+AE， OE+AE 的最小值为线段 O1A 的长 BNOBNO145，ONO1N， ANO190 在 RtO1NA 中，O1A+ 故答案为：+ 11 【解答】解： （1）把点 C 坐标代入 yx， 解得：c6，则点 C（4，6） ， 一次函数交 y 轴于点 B， 函数表达式为：ykx+2， 把点 C 坐标代入上式，解得：k1， 故：k1，b2， 一次函数表达式为：yx+2； （2）当点 P 运动到点 B 的位置时，|PAPC|最大， 则点 P 坐标为（0，2） ； （3）以下各点的坐标分别为：B（0，2） ，C（4，6） ， 过点 C 作 CGDE，使 GCDE， 则
33、：四边形 DECG 为平行四边形， 作点 G 作关于 x 轴的对称点 F，连接 BF，交 x 轴于 D，点 D 即为所求点， 则点 G 坐标为（2，6） ，点 F 坐标为（2，6） ， 则：DFDGEC，DB+CEBD+DGBD+DFBF，即：BD+CE 最小， 而：DE、BC 长度为常数， 故：在图示位置时，四边形 BDEC 的周长取最小值， 把点 B、F 点坐标代入一次函数表达式：ymx+b， 解得：BF 所在的直线表达式为：y4x+2， 令：y0，则 x， 则：点 D 和 E 的坐标分别为（，0） 、 （，0） ， 由勾股定理得：BC4，CE，BD， 则：四边形 BDEC 的周长取最小值
34、2+4+2 12 【解答】解： （1）将点 B 坐标代入直线 l 的表达式得：m3，点 B（2，3） ， 令 y0，则 x2，即点 A（2，0） ， 将点 B、C 的坐标代入一次函数表达式：ykx+b 得：，解得：， 故：直线 BC 的表达式为：y3x+9； （2）过点 O 作 ODAB 交 BC 于点 D，则 D 点为所求， 直线 AB 表达式得 k 值为，则直线 OD 的表达式为 yx， 将直线 BC 与 OD 表达式联立并解得：x， 即：点 D 的坐标为（，） ； （3）过点 P 作 x 轴的平行线分别于过点 A、M 与 y 轴的平行线于点 G、H， 设点 P 的坐标为（0，n） 、点 M（m，93m） ， GPA+GAP90，GPA+HPM90，HPMGAP， 又 PAPM，GH90，AGPPHM（AAS） ， GPHM2，GAPH， 即：， 解得：m或， 即点 M 的坐标为（，）或（，） ； （4）t+BE+AE， 过点 A 作倾斜角为 45 度的直线 l2，过点 E 作 EFl2交于点 F， 则：EFAE，即 tBE+EF， 当 B、E、F 三点共线且垂直于直线 l2时，t 最小，即：tBF， 同理，直线 l2的表达式为：yx2，直线 BF 表达式为：yx+1， 将上述两个表达式联立并解得：x，即：点 F（，） ， tBF
