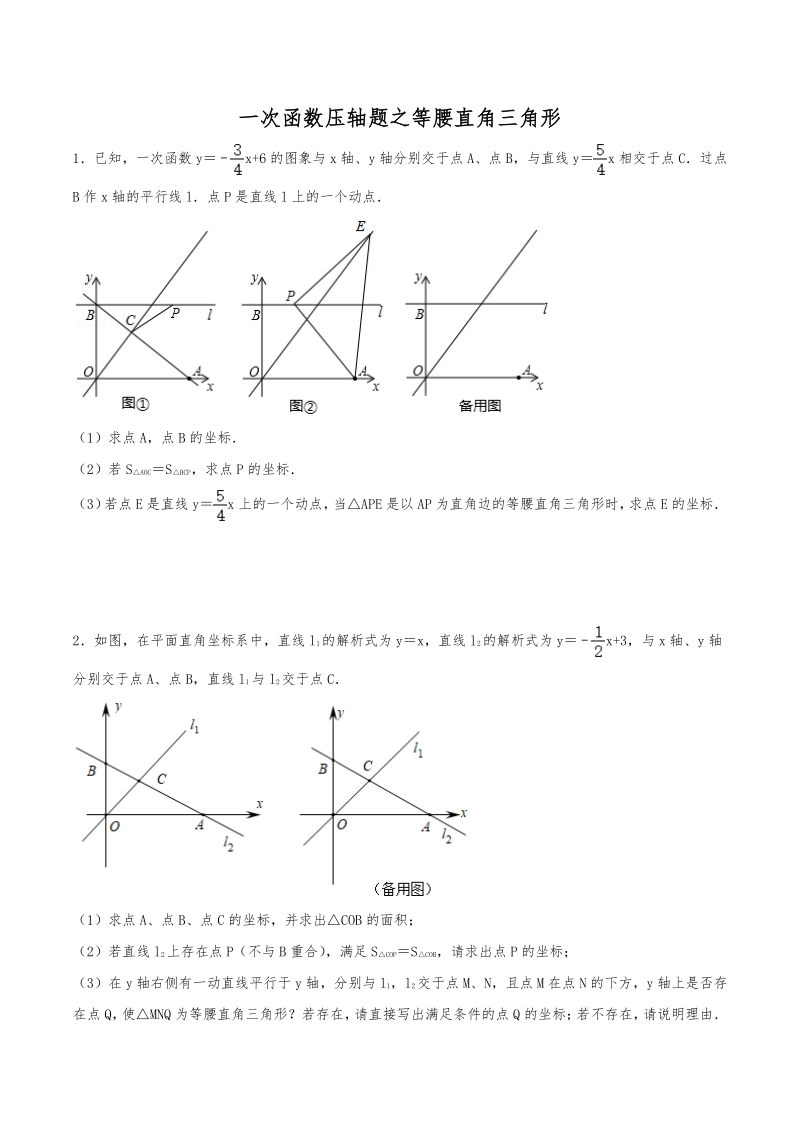
1、一次函数压轴题之等腰直角三角形一次函数压轴题之等腰直角三角形 1已知，一次函数 yx+6 的图象与 x 轴、y 轴分别交于点 A、点 B，与直线 yx 相交于点 C过点 B 作 x 轴的平行线 l点 P 是直线 l 上的一个动点 （1）求点 A，点 B 的坐标 （2）若 SAOCSBCP，求点 P 的坐标 （3） 若点 E 是直线 yx 上的一个动点， 当APE 是以 AP 为直角边的等腰直角三角形时， 求点 E 的坐标 2如图，在平面直角坐标系中，直线 l1的解析式为 yx，直线 l2的解析式为 yx+3，与 x 轴、y 轴 分别交于点 A、点 B，直线 l1与 l2交于点 C （1）求点
2、A、点 B、点 C 的坐标，并求出COB 的面积； （2）若直线 l2上存在点 P（不与 B 重合） ，满足 SCOPSCOB，请求出点 P 的坐标； （3）在 y 轴右侧有一动直线平行于 y 轴，分别与 l1，l2交于点 M、N，且点 M 在点 N 的下方，y 轴上是否存 在点 Q， 使MNQ 为等腰直角三角形？若存在， 请直接写出满足条件的点 Q 的坐标； 若不存在， 请说明理由 3如图 1，在平面直角坐标系中，直线 l1：yx+b 与直线 l2：yx8 交于点 A，已知点 A 的横坐标 为5，直线 l1与 x 轴交于点 B，与 y 轴交于点 C，直线 l2与 y 轴交于点 D （1）求直
3、线 l1的解析式； （2）将直线 l2向上平移 6 个单位得到直线 l3，直线 l3与 y 轴交于点 E，过点 E 作 y 轴的垂线 l4，若点 M 为 垂线 l4上的一个动点，点 N 为 x 轴上的一个动点，当 CM+MN+NA 的值最小时，求此时点 M 的坐标及 CM+MN+NA 的最小值； （3）在（2）条件下，如图 2，已知点 P、Q 分别是直线 l1、l2上的两个动点，连接 EP、EQ、PQ，是否存在 点 P、Q，使得EPQ 是以点 P 为直角顶点的等腰直角三角形，若存在，求点 P 的坐标，若不存在，说明理 由 4如图，在平面直角坐标系中，已知直线 BD：yx2 与直线 CE：yx+
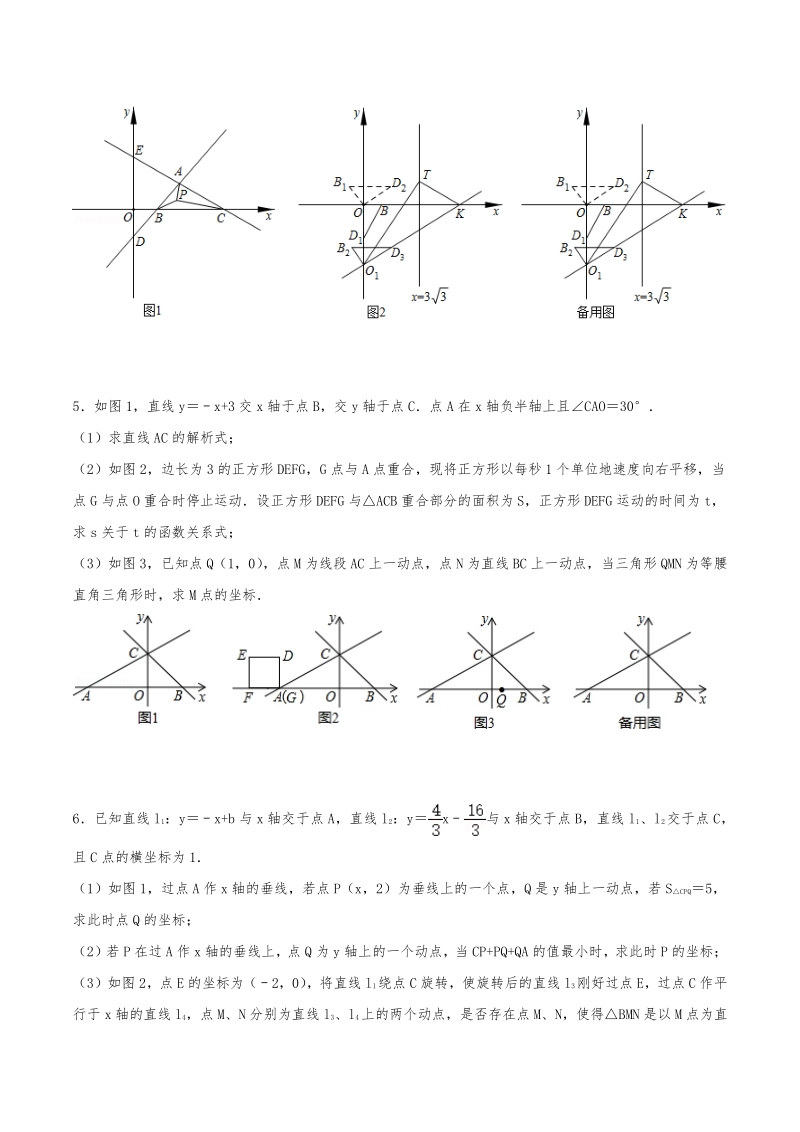
4、4 相交于点 A （1）求点 A 的坐标； （2）点 P 是ABC 内部一点，连接 PA、PB、PC，求 PB+PA+PC 的最小值； （3）将点 D 向下平移一个单位得到点 D1，连接 BD1，将OD1B 绕点 O 旋转至OB1D2的位置，使 B1D2x 轴， 再将OB1D2沿 y 轴向下平移得到O1B2D3，在平移过程中，直线 O1D3与 x 轴交于点 K，在直线 x3上任取 一点 T，连接 KT，O1T，O1KT 能否以 O1K 为直角边构成等腰直角三角形？若能，请直接写出所有符合条件 的 T 点的坐标；若不能，请说明理由 5如图 1，直线 yx+3 交 x 轴于点 B，交 y 轴于点
5、C点 A 在 x 轴负半轴上且CAO30 （1）求直线 AC 的解析式； （2）如图 2，边长为 3 的正方形 DEFG，G 点与 A 点重合，现将正方形以每秒 1 个单位地速度向右平移，当 点 G 与点 O 重合时停止运动设正方形 DEFG 与ACB 重合部分的面积为 S，正方形 DEFG 运动的时间为 t， 求 s 关于 t 的函数关系式； （3）如图 3，已知点 Q（1，0） ，点 M 为线段 AC 上一动点，点 N 为直线 BC 上一动点，当三角形 QMN 为等腰 直角三角形时，求 M 点的坐标 6已知直线 l1：yx+b 与 x 轴交于点 A，直线 l2：yx与 x 轴交于点 B，直
6、线 l1、l2交于点 C， 且 C 点的横坐标为 1 （1）如图 1，过点 A 作 x 轴的垂线，若点 P（x，2）为垂线上的一个点，Q 是 y 轴上一动点，若 SCPQ5， 求此时点 Q 的坐标； （2）若 P 在过 A 作 x 轴的垂线上，点 Q 为 y 轴上的一个动点，当 CP+PQ+QA 的值最小时，求此时 P 的坐标； （3）如图 2，点 E 的坐标为（2，0） ，将直线 l1绕点 C 旋转，使旋转后的直线 l3刚好过点 E，过点 C 作平 行于 x 轴的直线 l4，点 M、N 分别为直线 l3、l4上的两个动点，是否存在点 M、N，使得BMN 是以 M 点为直 角顶点的等腰直角三角
7、形？若存在，求出 N 点的坐标；若不存在，请说明理由 7如图，在矩形 ABCO 中，点 O 为坐标原点，点 B（4，3） ，点 A、C 在坐标轴上，点 Q 在 BC 边上，直线 L1： ykx+k+1 交 y 轴于点 A对于坐标平面内的直线，先将该直线向右平移 1 个单位长度，再向下平移 1 个单 位长度，这种直线运动称为直线的斜平移现将直线 L1经过 2 次斜平移，得到直线 L2 （1）求直线 L1与两坐标轴围成的面积； （2）求直线 L2与 AB 的交点坐标； （3）在第一象限内，在直线 L2上是否存在一点 M，使得AQM 是等腰直角三角形？若存在，请直接写出点 M 的坐标；若不存在，请说
8、明理由 8如图，直线 ykx+k 分别交 x 轴、y 轴于点 A，C，直线 BC 过点 C 交 x 轴于点 B，且 OAOC，CBA 45，点 P 是直线 BC 上的一点 （1）求直线 BC 的解析式； （2）若动点 P 从点 B 出发沿射线 BC 方向匀速运动，速度为个单位长度/秒，连接 AP，设PAC 的面积 为 S，点 P 的运动时间为 t 秒，求 S 与 t 之间的函数关系式，并写出 t 的取值范围； （3）若点 Q 是直线 AC 上且位于第三象限图象上的一个动点，点 M 是 y 轴上的一个动点，当以点 B、M、Q 为顶点的三角形为等腰直角三角形时，求点 Q 和点 M 的坐标 9如图，
9、在平面直角坐标系中，直线 AB：yx+与直线 AC：y+8 交于点 A，直线 AB 分别交 x 轴、y 轴于 B、E，直线 AC 分别交 x 轴、y 轴于点 C、D （1）求点 A 的坐标； （2）在 y 轴左侧作直线 FGy 轴，分别交直线 AB、直线 AC 于点 F、G，当 FG3DE 时，过点 G 作直线 GH y 轴于点 H，在直线 GH 上找一点 P，使|PFPO|的值最大，求出 P 点的坐标及|PFPO|的最大值； （3）将一个 45角的顶点 Q 放在 x 轴上，使其角的一边经过 A 点，另一边交直线 AC 于点 R，当AQR 为等 腰直角三角形时，请直接写出点 R 的坐标 10如
10、图，已知直线 yx+4 与 x 轴、y 轴分别相交于点 A、B，点 C 从 O 点出发沿射线 OA 以每秒 1 个单 位长度的速度匀速运动，同时点 D 从 A 点出发沿 AB 以每秒 1 个单位长度的速度向 B 点匀速运动，当点 D 到 达 B 点时 C、D 都停止运动点 E 是 CD 的中点，直线 EFCD 交 y 轴于点 F，点 E与 E 点关于 y 轴对称点 C、D 的运动时间为 t（秒） （1）当 t1 时，AC ，点 D 的坐标为 ； （2）设四边形 BDCO 的面积为 S，当 0t3 时，求 S 与 t 的函数关系式； （3）当直线 EF 与AOB 的一边垂直时，求 t 的值； （
11、4）当EFE为等腰直角三角形时，直接写出 t 的值 11 如图 1， 在平面直角坐标系中， O 为坐标原点， 直线 l： yx+m 与 x、 y 轴的正半轴分别相交于点 A、 B，过点 C（4，4）画平行于 y 轴的直线交直线 AB 于点 D，CD10 （1）求点 D 的坐标和直线 l 的解析式； （2）求证：ABC 是等腰直角三角形； （3） 如图 2， 将直线 l 沿 y 轴负方向平移， 当平移适当的距离时， 直线 l 与 x、 y 轴分别相交于点 A、 B， 在直线 CD 上存在点 P，使得ABP 是等腰直角三角形请直接写出所有符合条件的点 P 的坐标 （不必 书写解题过程） 1 【解答
12、】解： （1）一次函数 yx+6 的图象与 x 轴、y 轴分别交于点 A、点 B， 则点 A、B 的坐标分别为： （8，0） 、 （0，6） ； （2）联立 yx+6、yx 并解得：x3，故点 C（3，） ， SAOC815SBCPBP（yPyC）BP（6） ， 解得：BP， 故点 P（，6）或（，6） （3）设点 E（m，m） 、点 P（n，6） ； 当EPA90时，如左图， MEP+MPE90，MPE+NPA90， MEPNPA，APPE，EMPPNA（AAS） ， 则 MEPN6，MPAN， 即|mn|6，m68n， 解得：m或 16， 故点 E（，）或（16，20） ； 当EAP90时
13、，如右图， 同理可得：AMPANE（AAS） ， 故 MPEN，AMAN6， 即mn8，|8m|6，解得：m2 或 14， 故点 E（2，）或（14，） ； 综上，E（，）或（14，）或； （2，）或（16，20） 2 【解答】解： （1）直线 l2的解析式为 yx+3，与 x 轴、y 轴分别交于点 A、点 B，则点 A、B 的坐标 分别为（6，0） 、 （0，3） ， 联立式 yx，yx+3 并解得：x2，故点 C（2，2） ； COB 的面积OBxC323； （2）设点 P（m，m+3） ， SCOPSCOB，则 BCPC， 则（m2） 2+（ m+32） 222+125， 解得：m4 或
14、 0（舍去 0） ， 故点 P（4，1） ； （3）设点 M、N、Q 的坐标分别为（m，m） 、 （m，3m） 、 （0，n） ， 当MQN90时， GNQ+GQN90，GQN+HQM90，MQHGNQ， NGQQHM90，QMQN， NGQQHM（AAS） ， GNQH，GQHM， 即：m3mn，nmm， 解得：m，n； 当QNM90时， 则 MNQN，即：3mmm，解得：m， nyN3； 当NMQ90时， 同理可得：n； 综上，点 Q 的坐标为（0，）或（0，）或（0，） 3 【解答】解： （1）点 A 的横坐标为5， A（5，3） ， 将点 A 代入 yx+b， b4， 直线 l1的解析
15、式 yx+4； （2）l2：yx8 与 y 轴的交点 D（0，8） ， 将直线 l2向上平移 6 个单位得到直线 l3，直线 l3与 y 轴交于点 E， E（0，2） ， 过点 E 作 y 轴的垂线 l4， 点 D 是点 C 关于直线 l4的对称点，作点 A 关于 x 轴的对称点 A（5，3） ， 连接 AD交 x 轴、l4于点 N、M，则此时 CM+MN+NA 最小，最小值为：AD， CM+MN+NAMD+MN+ANAD， AD； CM+MN+NA 的值最小为； （3）存在，理由： 设点 P、Q 的坐标分别为： （m，m+4） 、 （n，n8） ， 当点 E 在点 P 右边时，过点 Q 作
16、x 轴的平行线交 y 轴于点 M，过点 P 作 PNQM 于点 N，PN 交 l4于点 K， 则PNQEKP（AAS） ， PNKE，QNPK， 即：m+4+n+8m，mnm+4+2， 解得：m3， 点 P（3，） 当点 E 在点 P 的左侧时，同理可得： （，5） ， 故答案为： （3，）或（，5） ， 4 【解答】解： （1）直线，则点 B、D 的坐标分别为： （，0） 、 （0，2） ； 直线，则点 C、E 的坐标分别为： （4，0） 、 （0，4） ； 联立 BD、CE 的表达式并解得：x2，故点 A（2，2） ； （2）如图，将APB 绕点 C 逆时针旋转 60得到EFC，则BFP
17、是等边三角形，ECB90， BC3，ACCE， 在 RtEBC 中，BE， PA+PB+PCEF+FP+PBBE， PA+PB+PC， PA+PB+PC 的最小值为； （3）存在，理由： 点 D1（0，3） ，点 B（，0） ， 则BD1O30，B1D2x 轴，则直线 OD2的倾斜角为 30， 设直线 O1K 的表达式为：yx+m， 则点 O1（0，m） ，点 K（m，0） ， 则 MO1m，MKm，KNm，TN|m3|，则点 T（3，m） O1KT 能否以 O1K 为直角边构成等腰直角三角形，则 O1KTK，TKO1K， 过点 K 作 y 轴的平行线分别交过点 O1、T 与 x 轴的平行线于
18、点 M、N， NKT+NTK90，NKT+O1KM90， O1KMNTK，KNTO1MK90，O1KTK， KNTO1MK（AAS） ， TNKM，即：|m3|m， 解得：m， 故点 T（3，）或（3，） 5 【解答】解： （1）直线 yx+3 交 x 轴于点 B，交 y 轴于点 C，则点 B、C 的坐标为（3，0） 、 （0，3） ， CAO30，则 AC2OC6，则 OA3， 将点 A、C 的坐标代入一次函数表达式：ykx+b 并解得： 直线 AC 的表达式为：yx+3； （2）如图 2 所示： 当 0t3 时， （左侧图） ， 正方形的 DA 边交 AC 于点 H，点 A 运动到点 M
19、处， 则点 M（3+t，0） ，则点 H（3+t，t） ， SSAHMAMHMttt 2， 当 3t3时， （右侧图） ， 正方形的 DA 边交 AC 于点 H，点 A 运动到点 G 处，E、F 交直线 AC 于点 R、S， AGt，则 ASt3，则 RS（t3） ，同理 HGt， 同理可得：SS梯形 RSHG3（t+t）t； 故：S； （3）点 M 为线段 AC 上一动点， 经画图，MQN 分别为 90时，点 M 不在线段 AC 上， NMQ90时，三角形 QMN 为等腰直角三角形， 过点 M 作 y 轴的平行线交 x 轴于点 G，过点 N 作 x 轴的平行线交 MG 于点 R、交 y 轴于
20、点 H， 设点 M、N 的坐标分别为（m，m+3） 、 （n，3n） ， NMR+RNM90，MNR+GMQ90， GMQRNM， NRMMGO90，MRMQ， NRMMGO（AAS） ， 则 MGRN，GQRM， 即：nmm+3，3n（m+3）1m， 解得：m2， 故点 M 的坐标为（2，1） ； 当MNQ90时， 同理可得：点 M（，2） ； 综上，点 M 的坐标为： （2，1）或（，2） 6 【解答】解： （1）直线 l2：yx，令 x1，则 y4，故 C（1，4） ， 把 C（1，4）代入直线 l1：yx+b，得：b3，则 l1为：yx3，所以 A（3，0） ， 所以点 P 坐标为（3
21、，2） ，如图，设直线 AC 交 y 轴于点 M， 设 yPC：ymx+t 得：，解得， yPC1.5x2.5，即 M（0，2.5） SCPQQM（xCxP）（yQ+2.5）45，解得：yQ0 或5， Q 的坐标为（0，0）或（0，5） ； （2）确定 C 关于过 A 垂线的对称点 C（7，4） 、A 关于 y 轴的对称点 A（3，0） ， 连接 AC交过 A 点的垂线与点 P，交 y 轴于点 Q，此时，CP+PQ+QA 的值最小， 将点 A、C点的坐标代入一次函数表达式：ykx+b得： 则直线 AC的表达式为：yx， 即点 P 的坐标为（3，） ， （3）将 E、C 点坐标代入一次函数表达式
22、，同理可得其表达式为：yx 当点 M 在直线 l4上方时，设点 N（n，4） ，点 M（s，s） ，点 B（4，0） ， 过点 N、B 分别作 y 轴的平行线交过点 M 与 x 轴的平行线分别交于点 R、S， RMN+RNM90，RMN+SMR90， SMRRNM， MRNMSB90，MNMB， MSBNRM（AAS） ， RNMS，RMSB， 即，解得：， 故点 N 的坐标为（16，4） ， 当点 M 在 l4下方时， 同理可得：N（，4） ， 即：点 N 的坐标为（，4）或（16，4） 7 【解答】解： （1）将点 A（0，3）代入直线 L1：ykx+k+1 并解得：k2， 故 L1的表达
23、式为：y2x+3， 设：L1与 x 轴交点坐标为 D，则其坐标为（，0） ， 直线 l1与两坐标轴围成的面积ODAO3； （2）将直线 L1经过 2 次斜平移，得到直线 L2：y2（x2）+322x3， 当 y3 时，x3， 即直线 L2与 AB 的交点坐标为（3，3） ； （3）当QAM 为直角时，点 M 在第四象限，舍去； 当AQM 为直角时， 对于 L2，当 x4 时，y5， 故点 M（4，5） （舍去） ； 当AMQ 为直角时，AMMQ， 过点 M 作 x 轴的平行线分别交 AO、BC 于点 G、H， 设点 M（m，2m3） ，点 Q（4，n） ， AMG+GAM90，AMG+QMH9
24、0， QMHGAM，AGMMHQ90，AMMQ， AGMMHQ（AAS） ， AGMH，即：|32m+3|4m， 解得：m2 或， 故点 M（，）或（2，1） ， 故点 M（，）或（2，1） 8 【解答】解： （1）直线 ykx+k 分别交 x 轴、y 轴于点 A，C，则点 A（1，0） ， 且 OAOC，则点 C（0，3） ，则 k3， 故直线 AC 的表达式为：y3x+3， CBA45，OBOC3，点 B（3，0） ， 点 C（0，3） 、点 B（3，0） ，则直线 BC 的表达式为：yx+3； （2）当点 P 在线段 BC 时， 过点 P 作 PHx 轴于点 H， CBA45，PHPBs
25、in45tt， SSABCSABPBA（OCPH）4（3t）62t， （0t3） ； 当点 P 在 y 轴右侧的射线 BC 上时， 同理可得：SSABPSABC2t6， （t3） ； 故 S； （3）设点 M（0，m） ，点 Q（n，3n+3） ， 如图 2（左侧图） ， 当BMQ90时， （点 M 在 x 轴上方） ， 分别过点 Q、P 作 y 轴的平行线 QG、BH，过点 M 作 x 轴的平行线分别交 GQ、BH 于点 G、H， GMQ+MQG90，GMQ+HMB90， HMBGQM， MHBQGM90，MBMQ， MHBQGM（AAS） ， GQMH，BHGM， 即：mn，m3n33，
26、解得：m，n； 故点 M（0，） 、点 Q（，） ； 同理当点 M 在 x 轴下方时， 3n+3m3 且mn，解得：mn0（舍去） ； 当MQB90时， 同理可得：n3n3，3n+3m3n， 解得：m6，n， 故点 M（0，6） 、点 Q（，） ； 当QBM90时， 同理可得：3n33，m3n 解得：m5，n2， 点 M（0，5） 、点 Q（2，3） ； 综上，M（0，） 、Q（，）或 M（0，6） 、Q（，）或 M（0，5）点 Q（2，3） 9 【解答】解： （1）联立，解得：， 故点 A 的坐标为（2，7） ； （2）由题意得：点 E、D、B、C 的坐标分别为（0，） 、 （0，8） 、
27、（，0） 、 （16，0） ， 过点 A 作 MNx 轴，分别交 FG、DE 于点 M、N，则：AN2， FGDE， AFGAED， 3，则 AM6， 点 M 的横坐标为：8， 则点 F、G 的坐标分别为（8，） 、 （8，4） ， 在 y 轴上找到点 O 关于直线 GH 的对称点 O（0，8） ，连接 FO并延长，交直线 GH 于点 P， 此时，|PFPO|的值最大，最大值为 PO， 直线 OF 的表达式为：yx+8，当 y4 时，x，即点 P 坐标为（，4） ， |PFPO|FO， 故：点 P 坐标为（，4） ，|PFPO|； （3）AQR 为等腰直角三角形，有如下图所示的两种情况， 当
28、AQAC， 当点 R 在点 A 下方时， 直线 AQ 的表达式为：y2x+b，将点 A 坐标代入得：72（2）+b，解得：b3， 故：直线 AQ 的表达式为：y2x+3，则点 Q 坐标为（，0） ， 过点 A 作 x 轴的平行线，过点 R 作 y 轴的平行线，过点 Q 作 y 轴的平行线，围成矩形 GMQH， GAR+QAH90，QAH+AQH90， AQHGAR， AGRQHA90，ARAQ， AGRQHA（AAS） ， HQGA7，GRAH2+，OM2+GA9， RM7 故点 R 的坐标为（9，） ， 当点 R 在点 A 上方时， 同理可得点 R 坐标为（5，） ； 当 RQAC 时， 同
29、理，点 R的坐标为（12，14）或（，） ， 故：点 R 的坐标为（9，）或（5，）或（12，14）或（，） 10 【解答】解： （1）如图 1，过 D 作 DHAC 于 H， 直线 yx+4 与 x 轴、y 轴分别相交于点 A，A、B， A（3，0） ，B（0，4） ， AO3，BO4， AB5， 当 0t3 时，如图 1， COt，ADt， AC3t，DHAD sinBAOt，AHADcosBAOt， 当 t1 时，AC312， 点 D 的坐标为（，） ； （2）AO3，BO4，AB5 sinBAO，cosBAO 过 D 作 DHAC 于 H， 当 0t3 时，如图 1， COt，ADt，
30、 AC3t，DHAD sinBAOt， SSABOSADC34（3t） t， St 2 t+6（0t3） （3）如图 2，当 EFBO 时， EFCD， CDBO， ACD90， 在 RtADC 中，cosBAO， ， t， 当 EFAB 时，如图 3， EFCD， 直线 CD 和直线 AB 重合， C 点和 A 点重合， t3 （4）如图 4， 当 0t，且且重叠部分为等腰梯形 PEQM 时， 则PEQMQE， 菱形 CDMN， CDMN， MQECEQ， EFCD， 即CEF90， CEQ45， ACDCEQ45， 过 D 作 DHAC 于 H，则DHC 是等腰直角三角形， DHHC， t
31、3tt， t； 如图 5， 当t5，且重叠部分为等腰梯形 EHNK 时， 同理可得CHE45， 连接 DHDH， EF 垂直平分 CD， CHDH，DHECHE45， DHC90， DHt， 而 CHCOHOCO（AOAH）t（3t） ， t（3t）t， t 11 【解答】解： （1）CD10，点 C 的坐标为（4，4） ， 点 D 的坐标为（4，6） ， 把点 D（4，6）代入得，m4 直线 l 的解析式是； （2）， A（8，0） ，B（0，4） ， 过点 C 画 CHy 轴于 H，则 CHOH4，BH8 在AOB 和BHC 中， AOBH，AOBBHC，BOCH， AOBBHC， ABBC，HBCOAB， ABC90， ABC 是等腰直角三角形； （3）p（4，）或（4，8）或（4，12）或（4，4）或（4，4）
