1、2020 年湖南省邵阳市邵阳县中考数学质年湖南省邵阳市邵阳县中考数学质量量检检查查试卷试卷 一、选择题：本大题共一、选择题：本大题共 10 个小题，每小题个小题，每小题 3 分，共分，共 30 分在每小题给出的四个选项中，只有一项是符合分在每小题给出的四个选项中，只有一项是符合 题目要求的题目要求的 12 的绝对值的倒数是（ ） A B2 C D2 2下列计算正确的是（ ） Ax3x2x6 B （a3+1） （a31）a91 C D 3如图，ABCD，CDE140，则A 的度数为（ ） A140 B60 C50 D40 4纳米是一种长度单位，1 纳米0.000 000 001 米，已知某种花粉
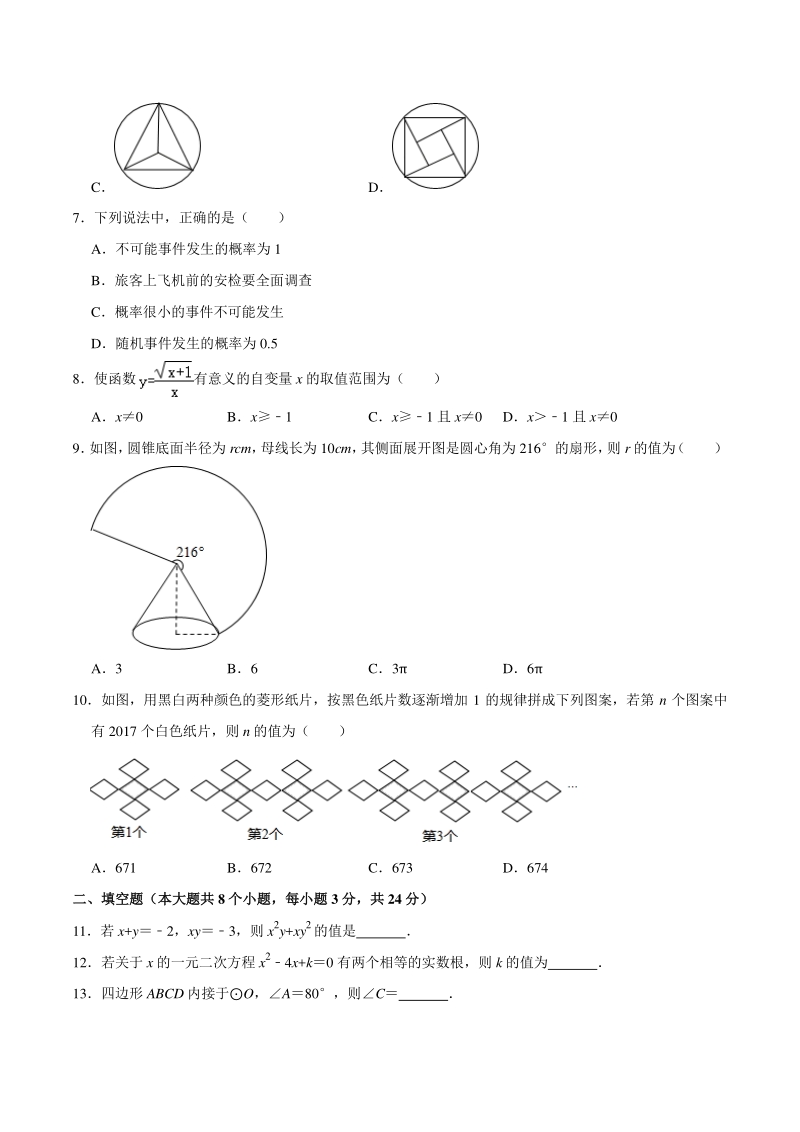
2、的直径为 5300 纳米，这种花粉的直径用 科学记数法表示为（ ） A5.310 4 米 B5.310 5 米 C5.310 6 米 D5.310 7 米 5如图是某个几何体的三视图，该几何体是（ ） A圆锥 B三棱锥 C圆柱 D三棱柱 6下列图形中，既是轴对称图形又是中心对称图形的是（ ） A B C D 7下列说法中，正确的是（ ） A不可能事件发生的概率为 1 B旅客上飞机前的安检要全面调查 C概率很小的事件不可能发生 D随机事件发生的概率为 0.5 8使函数有意义的自变量 x 的取值范围为（ ） Ax0 Bx1 Cx1 且 x0 Dx1 且 x0 9 如图， 圆锥底面半径为 rcm，
3、母线长为 10cm， 其侧面展开图是圆心角为 216的扇形， 则 r 的值为 （ ） A3 B6 C3 D6 10如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加 1 的规律拼成下列图案，若第 n 个图案中 有 2017 个白色纸片，则 n 的值为（ ） A671 B672 C673 D674 二、填空题（本大题共二、填空题（本大题共 8 个小题，每小题个小题，每小题 3 分，共分，共 24 分）分） 11若 x+y2，xy3，则 x2y+xy2的值是 12若关于 x 的一元二次方程 x24x+k0 有两个相等的实数根，则 k 的值为 13四边形 ABCD 内接于O，A80，则C 14不等
4、式组的解集是 15如图，在O 中，弦 AC2，点 B 是圆上一点，且ABC45，则O 的半径 R 16如图，已知平行四边形 ABCD 中，BCD 的平分线交边 AD 于 E，ABC 的平分线交 AD 于 F，若 AB 12，AE5，则 EF 17 小明在离路灯底部 6m 处测得自己的影子长为 1.2m， 小明的身高为 1.6m， 那么路灯的高度为 m 18等腰三角形的底和腰是方程 x26x+80 的两根，则这个三角形的周长为 三、解答题：本大题共三、解答题：本大题共 8 个小题，第个小题，第 1925 题每小题题每小题 8 分，第分，第 26 题题 10 分，共分，共 66 分解答题写出文字说
5、分解答题写出文字说 明、证明过程或演算步骤明、证明过程或演算步骤 19 （8 分）计算： 20 （8 分）先化简，再求值，其中 x 是从 2，2 和中选取的一个合适的数， 21 （8 分）为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答 100 道选择题，答对一题得 1 分，不答或错答不得分、不扣分，赛后对全体参赛选手的答题情况进行了 相关统计，整理并绘制成如下图表： 组别 分数段 频数（人） 频率 1 50 x60 30 0.1 2 60 x70 45 0.15 3 70 x80 60 n 4 80 x90 m 0.4 5 90 x100 45 0.15 请
6、根据以图表信息，解答下列问题： （1）表中 m ，n ； （2）补全频数分布直方图； （3）全体参赛选手成绩的中位数落在第几组； （4）若得分在 80 分以上（含 80 分）的选手可获奖，记者从所有参赛选手中随机采访 1 人，求这名选手 恰好是获奖者的概率 22 （8 分）如图，已知 ADBC，ACBD （1）求证：ADBBCA； （2）OA 与 OB 相等吗？若相等，请说明理由 23 （8 分）由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防 雾霾口罩共 20 万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表： 甲 乙 原料成本 12 8
7、销售单价 18 12 生产提成 1 0.8 （1）若该公司五月份的销售收入为 300 万元，求甲、乙两种型号的产品分别是多少万只？ （2） 公司实行计件工资制， 即工人每生产一只口罩获得一定金额的提成， 如果公司六月份投入总成本 （原 料总成本+生产提成总额）不超过 239 万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润 最大？并求出最大利润（利润销售收入投入总成本） 24 （8 分）如图，AB 是长为 5m，倾斜角为 37的自动扶梯，平台 BD 与大楼 CE 垂直，且与扶梯 AB 的长 度相等，在 B 处测得大楼顶部 C 的仰角为 65，求大楼 CE 的高度（结果保留整数） （参
8、考数据： ，） 25 （8 分）如图，在ABC 中，ABAC，点 D 在 BC 上，BDDC，过点 D 作 DEAC，垂足为 E，O 经过 A，B，D 三点 （1）求证：AB 是O 的直径； （2）判断 DE 与O 的位置关系，并加以证明； （3）若O 的半径为 6，BAC60，求 DE 的长 26 （10 分）如图，已知抛物线 yx2+bx+c 经过 A（3，0） ，B（0，3）两点 （1）求此抛物线的解析式和直线 AB 的解析式； （2）如图，动点 E 从 O 点出发，沿着 OA 方向以 1 个单位/秒的速度向终点 A 匀速运动，同时，动点 F 从 A 点出发，沿着 AB 方向以个单位/秒
9、的速度向终点 B 匀速运动，当 E，F 中任意一点到达终点时 另一点也随之停止运动，连接 EF，设运动时间为 t 秒，当 t 为何值时，AEF 为直角三角形？ （3）如图，取一根橡皮筋，两端点分别固定在 A，B 处，用铅笔拉着这根橡皮筋使笔尖 P 在直线 AB 上方的抛物线上移动，动点 P 与 A，B 两点构成无数个三角形，在这些三角形中是否存在一个面积最大 的三角形？如果存在，求出最大面积，并指出此时点 P 的坐标；如果不存在，请简要说明理由 2020 年湖南省邵阳市邵阳县中考数学质检试卷年湖南省邵阳市邵阳县中考数学质检试卷 参考答案与试题解析参考答案与试题解析 一、选择题：本大题共一、选择
10、题：本大题共 10 个小题，每小题个小题，每小题 3 分，共分，共 30 分在每小题给出的四个选项中，只有一项是符合分在每小题给出的四个选项中，只有一项是符合 题目要求的题目要求的 12 的绝对值的倒数是（ ） A B2 C D2 【分析】 首先根据负数的绝对值等于它的相反数求出2 的绝对值， 然后利用乘积为 1 的两数互为倒数， 用 1 除以求出的绝对值即可得到最后结果 【解答】解：|2|2，而 2 的倒数为 12， 2 的绝对值的倒数是 故选：C 2下列计算正确的是（ ） Ax3x2x6 B （a3+1） （a31）a91 C D 【分析】根据同底数幂的运算法则、平方差公式、算术平方根以及
11、立方根的意义对各项进行判断即可 【解答】解：Ax3x2x5，故选项 A 错误； B （a3+1） （a31）a61，故选项 B 错误； C|a|，故选项 C 错误； Da，正确 故选：D 3如图，ABCD，CDE140，则A 的度数为（ ） A140 B60 C50 D40 【分析】先求出CDE 的邻补角，再根据两直线平行，内错角相等解答 【解答】解：CDE140， ADC18014040， ABCD， AADC40 故选：D 4纳米是一种长度单位，1 纳米0.000 000 001 米，已知某种花粉的直径为 5300 纳米，这种花粉的直径用 科学记数法表示为（ ） A5.310 4 米 B5
12、.310 5 米 C5.310 6 米 D5.310 7 米 【分析】先把 5300 纳米换算成 530010 9 米，再用科学记数法表示 【解答】解：由题意可知：5300 纳米530010 9 米5.310 6 米 故选：C 5如图是某个几何体的三视图，该几何体是（ ） A圆锥 B三棱锥 C圆柱 D三棱柱 【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状 【解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出这个几何体应该 是三棱柱 故选：D 6下列图形中，既是轴对称图形又是中心对称图形的是（ ） A B C D 【分析】根据轴对称图形与中心对称
13、图形的概念求解 【解答】解：A、既是轴对称图形又是中心对称图形，故此选项正确； B、是轴对称图形，不是中心对称图形，故此选项错误； C、既是轴对称图形又是中心对称图形，故此选项错误； D、不是轴对称图形，是中心对称图形，故此选项错误； 故选：A 7下列说法中，正确的是（ ） A不可能事件发生的概率为 1 B旅客上飞机前的安检要全面调查 C概率很小的事件不可能发生 D随机事件发生的概率为 0.5 【分析】根据概率的意义和必然发生的事件的概率 P（A）1、不可能发生事件的概率 P（A）0，随 机事件发生的概率在 0 与 1 之间，A、D、C 进行判定；根据全面调查的定义对 B 进行判定 【解答】解
14、：A、不可能事件发生的概率为 0，所以 A 选项错误； B、旅客上飞机前的安检要全面调查，所以 B 选项正确； C、概率很小的事件不是不可能发生，而是发生的机会较小，所以 C 选项错误； D、随机事件发生的概率在 0 与 1 之间，所以 D 选项错误 故选：B 8使函数有意义的自变量 x 的取值范围为（ ） Ax0 Bx1 Cx1 且 x0 Dx1 且 x0 【分析】根据被开方数大于等于 0，分母不等于 0 列式计算即可得解 【解答】解：由题意得，x+10 且 x0， 解得 x1 且 x0 故选：C 9 如图， 圆锥底面半径为 rcm， 母线长为 10cm， 其侧面展开图是圆心角为 216的扇
15、形， 则 r 的值为 （ ） A3 B6 C3 D6 【分析】直接根据弧长公式即可得出结论 【解答】解：圆锥底面半径为 rcm，母线长为 10cm，其侧面展开图是圆心角为 216的扇形， 2r210，解得 r6 故选：B 10如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加 1 的规律拼成下列图案，若第 n 个图案中 有 2017 个白色纸片，则 n 的值为（ ） A671 B672 C673 D674 【分析】将已知三个图案中白色纸片数拆分，得出规律：每增加一个黑色纸片时，相应增加 3 个白色纸 片；据此可得第 n 个图案中白色纸片数，从而可得关于 n 的方程，解方程可得 【解答】解：第
16、 1 个图案中白色纸片有 41+13 张； 第 2 个图案中白色纸片有 71+23 张； 第 3 个图案中白色纸片有 101+33 张； 第 n 个图案中白色纸片有 1+n33n+1（张） ， 根据题意得：3n+12017， 解得：n672， 故选：B 二、填空题（本大题共二、填空题（本大题共 8 个小题，每小题个小题，每小题 3 分，共分，共 24 分）分） 11若 x+y2，xy3，则 x2y+xy2的值是 6 【分析】根据提公因式法，把（x2y+xy2）分解因式，进而将已知条件代入求出即可 【解答】解：x2y+xy2 xy（x+y） ， 当 x+y2，xy3 时， 原式3（2） 6； 故
17、答案为：6 12若关于 x 的一元二次方程 x24x+k0 有两个相等的实数根，则 k 的值为 4 【分析】根据判别式的意义得到（4）24k0，然后解一次方程即可 【解答】解：根据题意得（4）24k0， 解得 k4 故答案为 4 13四边形 ABCD 内接于O，A80，则C 100 【分析】由四边形 ABCD 内接于O，A80，根据圆的内接四边形的对角互补，即可求得答案 【解答】解：四边形 ABCD 内接于O，A80， C180A100 故答案为：100 14不等式组的解集是 x3 【分析】分别求出各不等式的解集，再求出其公共解集即可 【解答】解：解不等式 2x15，得 x3； 解不等式 84
18、x0，得 x2； 不等式组的解集为 x3， 故答案为：x3 15如图，在O 中，弦 AC2，点 B 是圆上一点，且ABC45，则O 的半径 R 2 【分析】由圆周角定理得出AOC90，根据等腰直角三角形的性质即可得出答案 【解答】解：ABC45， AOC2ABC90， OAOCR， AOC 是等腰直角三角形， ROAOCAC2 故答案为：2 16如图，已知平行四边形 ABCD 中，BCD 的平分线交边 AD 于 E，ABC 的平分线交 AD 于 F，若 AB 12，AE5，则 EF 7 【分析】根据平行四边形的性质可得 ADBC，根据两直线平行内错角相等可得AFBFBC，再由角 平分线的定义可
19、得ABFFBC，从而不难推出AFBABF，由等角对等边可得 ABAF，已知 AE 的长，从而 EF 的长不难求解 【解答】解：四边形 ABCD 是平行四边形， ADBC， AFBFBC， BF 平分ABC， ABFFBC， AFBABF， ABAF； AB12，AE5， EFAFAE1257， 故答案为：7 17 小明在离路灯底部 6m 处测得自己的影子长为 1.2m， 小明的身高为 1.6m， 那么路灯的高度为 9.6 m 【分析】如图，设 AB 为小亮，CD 为路灯，DB6 米，利用相似三角形求得 CD 的长即可 【解答】解：如图，AB1.6m，DB6m，BE1.2m， ABDE，CDDE
20、， ABCD EABECD， ， AB1.6m，DB6m，BE1.2m， ， 解得：CD9.6， 故答案为：9.6 18等腰三角形的底和腰是方程 x26x+80 的两根，则这个三角形的周长为 10 【分析】由等腰三角形的底和腰是方程 x26x+80 的两根，解此一元二次方程即可求得等腰三角形的 腰与底边的长，注意需要分当 2 是等腰三角形的腰时与当 4 是等腰三角形的腰时讨论，然后根据三角形 周长的求解方法求解即可 【解答】解：x26x+80， （x2） （x4）0， 解得：x2 或 x4， 等腰三角形的底和腰是方程 x26x+80 的两根， 当 2 是等腰三角形的腰时，2+24，不能组成三角
21、形，舍去； 当 4 是等腰三角形的腰时，2+44，则这个三角形的周长为 2+4+410 这个三角形的周长为 10 故答案为：10 三、解答题：本大题共三、解答题：本大题共 8 个小题，第个小题，第 1925 题每小题题每小题 8 分，第分，第 26 题题 10 分，共分，共 66 分解答题写出文字说分解答题写出文字说 明、证明过程或演算步骤明、证明过程或演算步骤 19 （8 分）计算： 【分析】直接利用负整数指数幂的性质和零指数幂的性质、特殊角的三角函数值分别化简得出答案 【解答】解：原式119+2+4 119+1+4 6 20 （8 分）先化简，再求值，其中 x 是从 2，2 和中选取的一个
22、合适的数， 【分析】根据分式的加减乘除运算法则进行运算化简，然后选择 x代入求值即可 【解答】解：原式（） ， x2 且 x0， x， 则原式+2 21 （8 分）为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答 100 道选择题，答对一题得 1 分，不答或错答不得分、不扣分，赛后对全体参赛选手的答题情况进行了 相关统计，整理并绘制成如下图表： 组别 分数段 频数（人） 频率 1 50 x60 30 0.1 2 60 x70 45 0.15 3 70 x80 60 n 4 80 x90 m 0.4 5 90 x100 45 0.15 请根据以图表信息，解答下列
23、问题： （1）表中 m 120 ，n 0.2 ； （2）补全频数分布直方图； （3）全体参赛选手成绩的中位数落在第几组； （4）若得分在 80 分以上（含 80 分）的选手可获奖，记者从所有参赛选手中随机采访 1 人，求这名选手 恰好是获奖者的概率 【分析】 （1）根据表格可以求得全体参赛选手的人数，从而可以求得 m 的值，n 的值； （2）根据（1）中的 m 的值，可以将补全频数分布直方图； （3）根据表格可以求得全体参赛选手成绩的中位数落在第几组； （4）根据表格中的数据可以求得这名选手恰好是获奖者的概率 【解答】解： （1）由表格可得， 全体参赛的选手人数有：300.1300， 则 m3
24、000.4120，n603000.2， 故答案为：120，0.2； （2）补全的频数分布直方图如右图所示， （3）30+4575，75+60135，135+120255， 全体参赛选手成绩的中位数落在 80 x90 这一组， 即全体参赛选手成绩的中位数落在第 4 组； （4）由题意可得， ， 即这名选手恰好是获奖者的概率是 0.55 22 （8 分）如图，已知 ADBC，ACBD （1）求证：ADBBCA； （2）OA 与 OB 相等吗？若相等，请说明理由 【分析】 （1）根据 SSS 定理推出全等即可； （2）根据全等得出OABOBA，根据等角对等边得出即可 【解答】 （1）证明：在ADB
25、和BCA 中， ， ADBBCA（SSS） ； （2）解：OAOB， 理由是：ADBBCA， ABDBAC， OAOB 23 （8 分）由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防 雾霾口罩共 20 万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表： 甲 乙 原料成本 12 8 销售单价 18 12 生产提成 1 0.8 （1）若该公司五月份的销售收入为 300 万元，求甲、乙两种型号的产品分别是多少万只？ （2） 公司实行计件工资制， 即工人每生产一只口罩获得一定金额的提成， 如果公司六月份投入总成本 （原 料总成本+生产提成总额）不超
26、过 239 万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润 最大？并求出最大利润（利润销售收入投入总成本） 【分析】 （1）设甲型号的产品有 x 万只，则乙型号的产品有（20 x）万只，根据销售收入为 300 万元列 出方程，求出方程的解即可得到结果； （2）设安排甲型号产品生产 y 万只，则乙型号产品生产（20y）万只，根据公司六月份投入总成本（原 料总成本+生产提成总额）不超过 239 万元列出不等式，求出不等式的解集确定出 y 的范围，再根据利润 售价成本列出 W 与 y 的一次函数，根据 y 的范围确定出 W 的最大值即可 【解答】解： （1）设甲型号的产品有 x 万只，则
27、乙型号的产品有（20 x）万只， 根据题意得：18x+12（20 x）300， 解得：x10， 则 20 x201010， 则甲、乙两种型号的产品分别为 10 万只，10 万只； （2）设安排甲型号产品生产 y 万只，则乙型号产品生产（20y）万只， 根据题意得：13y+8.8（20y）239， 解得：y15， 根据题意得：利润 W（18121）y+（1280.8） （20y）1.8y+64， 当 y15 时，W 最大，最大值为 91 万元 24 （8 分）如图，AB 是长为 5m，倾斜角为 37的自动扶梯，平台 BD 与大楼 CE 垂直，且与扶梯 AB 的长 度相等，在 B 处测得大楼顶部
28、C 的仰角为 65，求大楼 CE 的高度（结果保留整数） （参考数据： ，） 【分析】作 BFAE 于点 F，则 BFDE，先在 RtABF 中，利用正弦三角函数可求出 BF 的长，再在 RtCDB 中，利用正切三角函数可求出 CD 的长，然后根据线段的和差即可得 【解答】解：如图，作 BFAE 于点 F，则 BFDE， 由题意得：BDAB5m，BDCE，BAF37，CBD65， 在 RtABF 中，sinBAF， 则 BFABsin3753（m） ， 在 RtCDB 中，tanCBD， 则 CDBDtan65511（m） ， 则 CEDE+CDBF+CD3+1114（m） ， 答：大楼 CE
29、 的高度约为 14m 25 （8 分）如图，在ABC 中，ABAC，点 D 在 BC 上，BDDC，过点 D 作 DEAC，垂足为 E，O 经过 A，B，D 三点 （1）求证：AB 是O 的直径； （2）判断 DE 与O 的位置关系，并加以证明； （3）若O 的半径为 6，BAC60，求 DE 的长 【分析】 （1）连接 AD，由 ABAC，BDCD，利用等腰三角形三线合一性质得到 ADBC，利用 90 的圆周角所对的弦为直径即可得证； （2）DE 与圆 O 相切，理由为：连接 OD，由 O、D 分别为 AB、CB 中点，利用中位线定理得到 OD 与 AC 平行，利用两直线平行内错角相等得到O
30、DE 为直角，再由 OD 为半径，即可得证； （3）由 ABAC，且BAC60，得到三角形 ABC 为等边三角形，设 AC 与O 交于点 F，连接 BF， DE 为三角形 CBF 中位线，求出 BF 的长，即可确定出 DE 的长 【解答】 （1）证明：连接 AD， ABAC，BDDC， ADBC， ADB90， AB 为圆 O 的直径； （2）DE 与圆 O 相切， 理由为：连接 OD， O、D 分别为 AB、BC 的中点， OD 为ABC 的中位线， ODBC， DEBC， DEOD， OD 为圆的半径， DE 与圆 O 相切； （3）解：ABAC，BAC60， ABC 为等边三角形， AB
31、ACBC12， 连接 BF， AB 为圆 O 的直径， AFBDEC90， AFCF6，DEBF， D 为 BC 中点， E 为 CF 中点，即 DE 为BCF 中位线， 在 RtABF 中，AB12，AF6，根据勾股定理得：BF6， DEBF3 26 （10 分）如图，已知抛物线 yx2+bx+c 经过 A（3，0） ，B（0，3）两点 （1）求此抛物线的解析式和直线 AB 的解析式； （2）如图，动点 E 从 O 点出发，沿着 OA 方向以 1 个单位/秒的速度向终点 A 匀速运动，同时，动点 F 从 A 点出发，沿着 AB 方向以个单位/秒的速度向终点 B 匀速运动，当 E，F 中任意一
32、点到达终点时 另一点也随之停止运动，连接 EF，设运动时间为 t 秒，当 t 为何值时，AEF 为直角三角形？ （3）如图，取一根橡皮筋，两端点分别固定在 A，B 处，用铅笔拉着这根橡皮筋使笔尖 P 在直线 AB 上方的抛物线上移动，动点 P 与 A，B 两点构成无数个三角形，在这些三角形中是否存在一个面积最大 的三角形？如果存在，求出最大面积，并指出此时点 P 的坐标；如果不存在，请简要说明理由 【分析】 （1）用待定系数法求出抛物线，直线解析式； （2）分两种情况进行计算即可； （3）方法 1、确定出面积达到最大时，直线 PC 和抛物线相交于唯一点，从而确定出直线 PC 解析式为 y x+
33、，根据锐角三角函数求出 BD，计算即可 方法 2、设出点 P 的坐标，进而表示出点 M 坐标，即可表示出 PM，最后用面积和即可得出二次函数， 即可得出结论 【解答】解： （1）抛物线 yx2+bx+c 经过 A（3，0） ，B（0，3）两点， ， ， yx2+2x+3， 设直线 AB 的解析式为 ykx+n， A（3，0） ，B（0，3） ， ， yx+3； （2）由运动得，OEt，AFt， OA3， AEOAOE3t， AEF 和AOB 为直角三角形，且EAFOAB， 如图 1， 当AOBAEF 时， ， ， t， 如图 2， 当AOBAFE 时， ， ， t1； （3）如图，存在， 过点
34、 P 作 PCAB 交 y 轴于 C， 直线 AB 解析式为 yx+3， 设直线 PC 解析式为 yx+b， 联立， x+bx2+2x+3， x23x+b30 94（b3）0 b， BC3，x， P（，） 过点 B 作 BDPC， 直线 BD 解析式为 yx+3， BD， BD， AB3 S最大ABBD3 即：存在面积最大，最大是，此时点 P（，） 方法 2、如图， 过点 P 作 PNx 轴于 N，交 AB 于 M， 设点 P（m，m2+2m+3） ， M（m，m+3） ， PMm2+2m+3+m3m2+3m， SSPABSPAM+SPBM（m2+3m）3（m23m）（m）2+， 当 m时，S最大，此时，P（，）
