1、2021 年中考复习二次函数压轴题分类训练年中考复习二次函数压轴题分类训练 1：与线段长度相关的综合题：与线段长度相关的综合题 1如图，直线 yx+2 与抛物线 yax2+bx+6（a0）相交于 A（，）和 B（4，m） ，点 P 是线段 AB 上 异于 A、B 的动点，过点作 PCx 轴于点 D，交抛物线于点 C （1）求抛物线的解析式； （2）如果设点 P 的坐标为（n，n+2） ，则点 C 的坐标可表示为 ； （3）请用含有 n 的式子表示 PC 的长，并确定 PC 长度的最大值 2在平面直角坐标系中，点 A 的坐标为（m，2m+3） ，过点 A 作 y 轴的平行线交二次函数 yx2的图
2、象于 点 B （1）点 B 的纵坐标为 （用含 m 的代数式表示） ； （2）当点 A 落在二次函数 yx2的图象上时，求 m 的值； （3）当 m0 时，若 AB2求 m 的值； （4）当线段 AB 的长度随 m 的增大而增大时，直接写出 m 的取值范围 3如图，直线 y1x+3 与 x 轴于交于点 B，与 y 轴交于点 C抛物线 y2x2+bx+c 经过 B、C 两点，并 与 x 轴另一个交点为 A （1）求抛物线 y2的解析式； （2）若点 M 在抛物线上，且 SMOC4SAOC，求点 M 的坐标； （3）设点 P 是线段 BC 上一动点，过 P 作 PQx 轴，交抛物线于点 Q，求线段
3、 PQ 长度的最大值 4如图，在平面直角坐标系中，已知抛物线 yax2+bx+与 x 轴交于 A（5，0） ，B（1，0）两点，与 y 轴交于点 C （）求抛物线的解析式； （）若点 M 是抛物线的顶点，连接 AM，CM，求ACM 的面积； （）若点 P 是抛物线上的一动点，过点 P 作 PE 垂直 y 轴于点 E，交直线 AC 于点 D，过点 D 作 x 轴 的垂线，垂足为点 F，连接 EF，当线段 EF 的长度最短时，求出点 P 的坐标 5如图，二次函数 yax2+bx+c 的图象与 x 轴交于 A，B 两点，其中 A 的坐标为（1，0） ，与 y 轴交于点 C（0，5） ，并经过点（1，
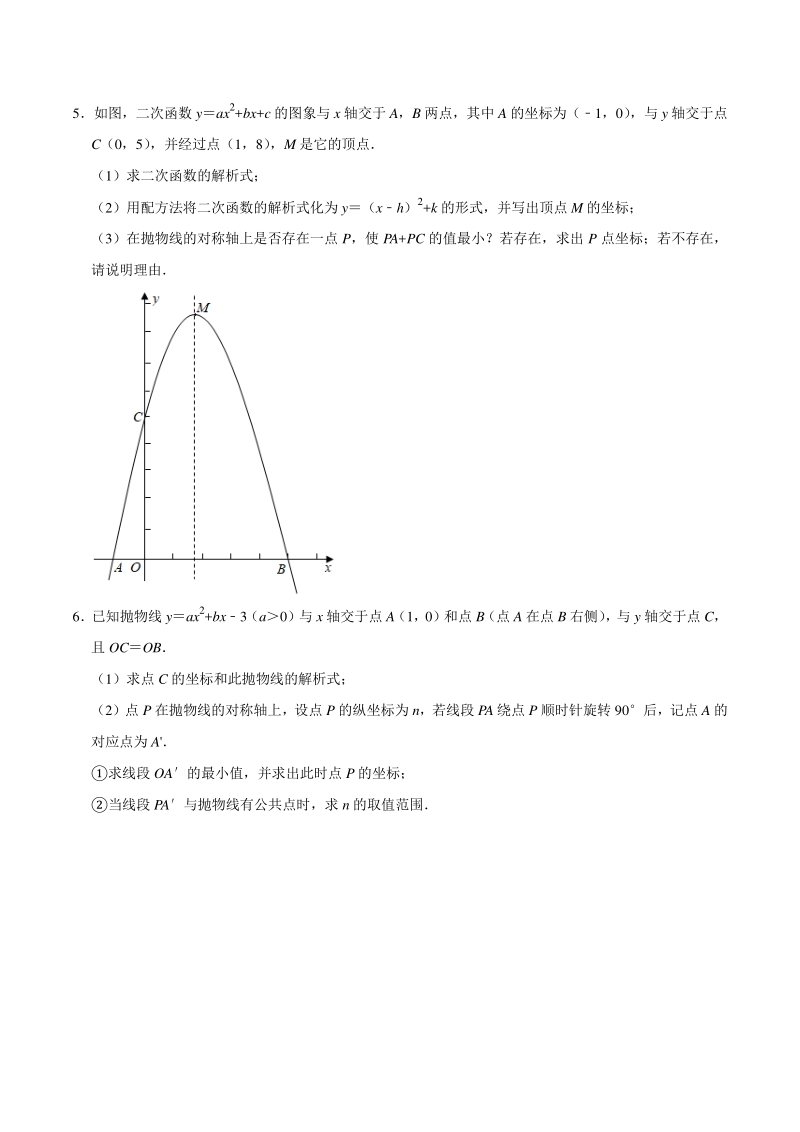
4、8） ，M 是它的顶点 （1）求二次函数的解析式； （2）用配方法将二次函数的解析式化为 y（xh）2+k 的形式，并写出顶点 M 的坐标； （3）在抛物线的对称轴上是否存在一点 P，使 PA+PC 的值最小？若存在，求出 P 点坐标；若不存在， 请说明理由 6已知抛物线 yax2+bx3（a0）与 x 轴交于点 A（1，0）和点 B（点 A 在点 B 右侧） ，与 y 轴交于点 C， 且 OCOB （1）求点 C 的坐标和此抛物线的解析式； （2）点 P 在抛物线的对称轴上，设点 P 的纵坐标为 n，若线段 PA 绕点 P 顺时针旋转 90后，记点 A 的 对应点为 A 求线段 OA的最小值
5、，并求出此时点 P 的坐标； 当线段 PA与抛物线有公共点时，求 n 的取值范围 7抛物线 yax2+bx+c 交 x 轴于 A（1，0） 、B（3，0）两点，顶点纵坐标为4 （1）求抛物线的解析式； （2）直线 l：ykxk（0k3）与抛物线交于 M（xM，yM） 、N（xN，yN） ，xMxN， 求 yM的范围； 点 P（xP，yP）在抛物线上（xMxPxN） ，点 Q（xQ，yQ）在直线 l 上，xPxQ，PQ 的长度记为 d对 于每一个 k，d 都有最大值，请求出 d 的最大值与 k 的函数关系式 8如图，已知抛物线 C1的顶点为 E（，） ，与 x 轴交于点 A、B（点 A 在点 B
6、 左侧） ，与 y 轴交于点 C（0，2） ； （1）求抛物线 C1的解析式； （2）点 D 是抛物线 C1上一点，且ACO+BCD45，求点 D 的坐标； （3） M 为抛物线在点 B 右侧上的一点， M 与 N 两点关于抛物线的对称轴对称， MB， NA 分别交 y 轴于 P、 Q 两点，求 OP2OQ 的值 9如图 1，抛物线 yax2+（a+3）x+3（a0）与 x 轴交于点 A（4，0） ，与 y 轴交于点 B，在 x 轴上有一 动点 E（m，0） （0m4） ，过点 E 作 x 轴的垂线交直线 AB 于点 N，交抛物线于点 P，过点 P 作 PM AB 于点 M （1）求 a 的值
7、和直线 AB 的函数表达式； （2）设PMN 的周长为 C1，AEN 的周长为 C2，若，求 m 的值； （3）如图 2，在（2）条件下，将线段 OE 绕点 O 逆时针旋转得到 OE，旋转角为 （090） ， 连接 EA、EB，求 EA+EB 的最小值 10抛物线 C：yx2+2x+3 与 x 轴负半轴交于点 A，与 y 轴交于点 B （1）写出 AB 的长； （2）如图 1，已知 C（0，2） ，点 E 是 x 轴正半轴上的点，OE 的垂直平分线 MN，交 OE 于点 F交 CE 于点 M，交抛物线 C 于点 N，若 MN2，求点 E 的坐标； （3）如图 2将抛物线 C 向左平移 1 个单
8、位长度，再向上平移 b（b0）个单位长度得到抛物线 C1，点 D 是抛物线 C1的顶点，点 P 是抛物线 C1在第一象限上的动点，PPy 轴，交抛物线 C1于点 P，直线 PO 交抛物线 C1于点 Q，直线 QP交 y 轴于 H，求证：HDOD 11如图，抛物线与 x 轴交于 A（1，0） 、B（3，0）两点，于 y 轴交于点 C（0，3） ，顶点为 D （1）求该抛物线的解析式及顶点 D 的坐标； （2）请计算以 A、B、D、C 为顶点的四边形的面积； （3）在 x 坐标轴上是否存在点 Q，使得 Q 点到 C、D 两点的距离之和最短，若存在，请直接写出 Q 点 坐标，若不存在，请说明理由 1
9、2如图 1，已知抛物线 yax22ax+b 与 x 轴交于点 A（2，0）和点 B，与 y 轴交于点 C（0，4） （1）求抛物线的函数解析式； （2）如图 2，已知点 P 是第四象限抛物线上的一点，且PAB2ACO，求点 P 的横坐标； （3）如图 3，点 D 为抛物线的顶点，直线 ykxk+2 交抛物线于点 E，F，过点 E 作 y 轴的平行线交 FD 的延长线于点 P，求 CP 的最小值 13如图 1，抛物线 yax2+c 与 x 轴交于点 A、B，与 y 轴交于点 C，P 为 x 轴下方抛物线上一点，若 OC 2OA4 （1）求抛物线解析式； （2）如图 2，若ABPACO，求点 P
10、的坐标； （3）如图 3，点 P 的横坐标为 1，过点 P 作 PEPF，分别交抛物线于点 E，F求点 A 到直线 EF 距离 的最大值 14已知抛物线与 x 轴交于点 A、B（点 A 在点 B 的左边） ，与 y 轴交于点 C （1）若 m1，求点 B 的坐标； （2）求出点 B、C 的坐标（用含 m 的式子表示） ； （3）若点 P 是线段 AB 上一点，过点 P 作 x 轴的垂线交抛物线于点 M，交直线 AC 于点 N，当线段 MN 长的最大值为时，求 m 的取值范围 15已知抛物线 yx22mx4m+4 经过定点 A （1）求 A 点坐标； （2）直线 yt（t6）与抛物线交于 B，C
11、 两点（B 在 C 的左边） ，过点 A 作 ADBC 于点 D，是否存 在 t 的值，使得对于任意的 m，DACABD 恒成立，若存在，请求 t 的值；若不存在，请说明理由 （3）如图，当 m1 时，直线 y2x 交对称轴于点 E，在直线 OE 的右侧作EOP 交抛物线于点 P，使 得 tanEOP，已知 x 轴上有一个点 M（t，0） ，EM+PM 是否存在最小值？若存在，求 t 的值；若不 存在，请说明理由 16如图，抛物线 yx2+bx+c 交 x 轴于点 A，B 两点，OA1，与 y 轴交于点 C，连接 AC，tanOAC3， 抛物线的对称轴与 x 轴交于点 D （1）求点 A，C
12、的坐标； （2）若点 P 在抛物线上，且满足PAB2ACO，求直线 PA 在与 y 轴交点的坐标； （3）点 Q 在抛物线上，且在 x 轴下方，直线 AQ，BQ 分别交抛物线的对称轴于点 M、N求证：DM+DN 为定值，并求出这个定值 参考答案参考答案 1解： （1）B（4，m）在直线 yx+2 上， m4+26， B（4，6） A（，） ，B（4，6）在抛物线 yax2+bx+6 上， ， 解得， 抛物线的解析式为 y2x28x+6； （2）设动点 P 的坐标为（n，n+2） ，则 C 点的坐标为（n，2n28n+6） 故答案是： （n，2n28n+6） ； （3）P（n，n+2） ，C（n
13、，2n28n+6） ， PC（n+2）（2n28n+6） ， 2n2+9n4， 2（n）2+， PC0， 当 n时，线段 PC 最大且为 2解： （1）根据题意知，点 B 的横坐标是 m， 将 xm 代入 yx2，得 ym2 即点 B 的纵坐标为 m2 故答案是：m2； （2）把 A（m，2m+3）代入 yx2，得2m+3m2 解得 m13，m21； （3）根据题意知：|2m+3m2|2 2m+3m22， 解得 m11，m21 m0， m1，符合题意； 2m+3m22， 解得 m11，m21 m0， m1，符合题意 综上所述，m 的值为1 或1； （4）由（2）知，当点 A、B 重合时，点 A
14、 的坐标是（3，9）或（1，1） 设 ABd， 当3m0 时，d2m+3m2（m+1）2+4 时，对称轴是直线 m1 且抛物线开口向下， 线段 AB 的长度随 m 的增大而增大时，3m1 当 m1 时，根据题意知，线段 AB 的长度随 m 的增大而增大时，m1 综上所述，m 的取值范围是3m1 或 m1 3解： （1）由直线 y1x+3 得：B（3，0） ，C（0，3） ， 将其代入 y2x2+bx+c，得 解得 故抛物线 y2的解析式是：y2x2+2x+3； （2）抛物线 y2的解析式 y2x2+2x+3（x3） （x+1）知，A（1，0） OA1 又C（0，3） ， OC3 设点 M 的坐
15、标为（x，x2+2x+3） ， SMOC4SAOC， 3|x|431， |x|4， x4， 当 x4 时，x2+2x+316+8+35； 当 x4 时，x2+2x+3168+321， 点 M 的坐标为（4，5）或（4，21） ； （3）设 P（a，a+3） ，此时 Q（a，a2+2a+3） ， PQa2+2a+3（a+3）a2+3a（a）2+ 该抛物线顶点坐标是（，） ，且开口向下， 当 a时，PQ 取最大值 4解： （）令 x0，则 y，即 C（0，） 设抛物线的表达式为 ya（xx1） （xx2）a（x5） （x+1） ， 将点 C 的坐标代入上式得：a（05） （0+1） ， 解得 a，
16、 故抛物线的表达式为 y（x5） （x+1）x2+2x+； （）由抛物线的表达式得顶点 M（2，） ， 过点 M 作 MHy 轴交 AC 于点 H， 设直线 AC 的表达式为 ykx+t，则， 解得， 故直线 AC 的表达式为 yx+， 当 x2 时，y，则 MH3， 则AMC 的面积SMHC+SMHAMHOA35； （）点 D 在直线 AC 上，设点 D（m，m+） ， 由题意得，四边形 OEDF 为矩形，故 EFOD，即当线段 EF 的长度最短时，只需要 OD 最短即可， 则 EF2OD2m2+（m+）2m2m+， 0，故 EF2存在最小值（即 EF 最小） ，此时 m1， 故点 D（1，
17、2） ， 点 P、D 的纵坐标相同， 故 2x2+2x+，解得 x2， 故点 P 的坐标为（2+，2）或（2，2） 5解： （1）二次函数 yax2+bx+c 的图象经过 A（1，0） ，C（0，5） ， （1，8） ， 则有：， 解得 抛物线的解析式为 yx2+4x+5 （2）yx2+4x+5（x24x+4）+5+4（x2）2+9， 二次函数的解析式化为 y（x2）2+9， 顶点 M 的坐标为（2，9） （3）存在，理由如下： 如图，由 A、B 关于对称轴对称，连接 BC 交对称轴于 P，连接 PA，此时 PA+PC 的值最小 由 yx2+4x+5（x5） （x+1）知 A（1，0） ，B（
18、5，0） ， B（5，0） ，C（0，5） ，设直线 BC 的解析式为 ymx+n（m0） ，则有 ， 解得 ， 直线 BC 的解析式为 yx+5 抛物线的对称轴 x2， P（2，3） 6解： （1）把 x0 代入 yax2+bx3，得：y3， 点 C 的坐标为（0，3） ， OC3， OBOC3， B（3，0） ， 把 A（1，0）和 B（3，0）代入 yax2+bx3，得：， 解得：， 此抛物线的解析式为 yx2+2x3； （2）由（1）可知：抛物线的对称轴为直线 x1， 设点 P（1，n） ， 当 n0 时，如图 1，设对称轴与 x 轴的交点为 M，过点 A作 ANPM 于 N， 线段
19、PA 绕点 P 顺时针旋转 90， APAP，APA90PMAPNA， NPA+APM90APM+PAM， NPAPAM， ANPPMA（AAS） ， ANPMn，PNAM2， 点 A（1n，n2） ， 当 n0 时，同理可得点 A（1n，n2） ， 当 n0 时，点 P 与点 M 重合，则点 A（1，2） ，符合 A（1n，n2） ， OA， 当 n时，OA有最小值为， 此时点 P（1，） ； 点 A（1n，n2） ， 点 A 在直线 yx3 上， 如图 2， 当线段 PA与抛物线有公共点， 则1n3 或1n0， n2 或 n1， 又当点 P 在抛物线顶点下方上，线段 PA与抛物线没有公共点
20、， n4， 综上所述：n2 或4n1 7解： （1）设抛物线的表达式为 ya（xx1） （xx2）a（x1） （x+3）a（x2+2x3） ， 函数的对称轴为 x（13）1， 当 x1 时，ya（x2+2x3）4a4， 解得 a1， 故抛物线的表达式为 yx2+2x3； （2）ykxkk（x1） ， 当 x1 时，ykxk0， 故该函数过点（1，0） ，即点 N（1，0） ， 故点 N、A 重合，如图： 联立， 整理得：x2+（2k）x+k30， 则 xM+xNk2， 而 xN1， 故 xMk3， 当 xk3 时，ykxkk（x1）k（k31）k24kyM， 0k3， 故4k24k0， 即 y
21、M的范围为4yM0； 由题意知，PQy 轴， 设点 P 的坐标为（x，x2+2x3） ，则点 Q（x，kxk） ， 则 PQkxkx22x+3x2+（k2）x+（3k） ， 10， 故 PQ 有最大值， 当 x时， PQ 的最大值为（）2+（k2） （）+（3k） ， 即 dmaxk22k+4 8解： （1）设抛物线的解析式为：ya（x）2， 将 C（0，2）代入得a2，解得 a1， y（x）2x2x2； （2）在 yx2x2 中，令 x0，得 y2，令 y0，得 x1 或 x2， C（0，2） ，A（1，0） ，B（2，0） ， OBOC2， BOC 为等腰直角三角形， OCB45， 当点
22、D 在 x 轴上方时， 设 CD 交 x 轴于点 Q， ACO+BCDQCO+BCD45， ACOQCO， 又AOCQOC90，OCOC， OACOCQ（ASA） ， OQOA1， Q（1，0） ， 由点 C、Q 的坐标得，直线 CQ 的表达式为 y2x2， 联立并解得， D（3，4） ； 当点 D 在 x 轴下方时， 将中的CBQ 沿着 BC 翻折得CBQ， 则 BQBQ1，QBQ90， Q（2，1） ， 同理可得：直线 CQ的表达式为 yx2， 联立并解得， D（，） ， 综上所述，D（3，4）或（，） ； （3）设 M（xM，yM） ，N（xN，yN） ， 设直线 MB 的解析式为：ym
23、（x2）， P（0，2m） ， 联立并整理得：x2（m+1）x+2m20， xB+xM2+xMm+1， xMm1， 同理可得：xNn+2， 又 M、N 关于对称轴对称， xM+xNm1+n+21， m+n0， OP2OQ2m2（n）2（m+n）0， 答：OP2OQ 的值为 0 9解： （1）令 y0，则 ax2+（a+3）x+30， （x+1） （ax+3）0， x1 或， 抛物线 yax2+（a+3）x+3（a0）与 x 轴交于点 A（4，0） ， 4， a A（4，0） ，B（0，3） ， 设直线 AB 解析式为 ykx+b，则， 解得， 直线 AB 解析式为 yx+3； （2）如图 1，
24、 PMAB，PEOA， PMNAEN， PNMANE， PNMANE， ， NEOB， ， AN（4m） ， 抛物线解析式为 yx2+x+3， PNm2+m+3（m+3）m2+3m， ， 解得 m2 或 4， 经检验 x4 是分式方程的增根， m2； （3） 如图 2， 在 y 轴上 取一点 M使得 OM， 连接 AM， 在 AM上取一点 E使得 OEOE OE2，OMOB34， OE2OMOB， ， BOEMOE， MOEEOB， ， MEBE， AE+BEAE+EMAM，此时 AE+BE最小（两点间线段最短，A、M、E共 线时） ， 最小值AM 10解： （1）对于 yx2+2x+3，令
25、yx2+2x+30，解得 x1 或 3，令 x0，则 y3， 故点 A、B 的坐标为（1，0） 、 （0，3） ， 则 AB； （2）如下图，设点 E 的坐标为（2m，0） ，则点 F（m，0） ，点 N（m，m2+2m+3） ， 由中点公式得，点 M 的坐标为（m，1） ， 则 MN|m2+2m+31|2， 解得 m2 或 0（舍去）或+1 或 1（舍去） ， 故 m2 或+1； （3）由 yx2+2x+3 得，其顶点为（1，4） ， 将抛物线 C 向左平移 1 个单位长度，再向上平移 b（b0）个单位长度得到抛物线 C1，则平移后的抛物 线表达式为 yx2+4+b， 则点 D（0，4+b）
26、 ， 设点 P 的坐标为（p，q） ，点 Q 的坐标为（s，t） ，则点 P的坐标为（p，q） ， 设直线 PQ 的表达式为 ykx，直线 PQ 的表达式为 ymx+n， 联立并整理得：x2+kx4b0，则 ps4b， 联立并整理得：x2+mx+n4b0，则psn4b， 由和得：n4b4+b，解得 n8+2b， 故点 H 的坐标为（0，8+2b） ， 则 HD8+2b4b4+bOD 11解： （1）设抛物线的表达式为 yax2+bx+c， 将点 A、B、C 的坐标代入抛物线表达式得：，解得， 故抛物线的表达式为 yx22x+3， 抛物线的对称轴为 x1，当 x1 时，yx22x+34， 故点
27、D 的坐标为（1，4） ； （2）由点 B、C、D 的坐标知，BC218，CD22，BD220， 则 BC2+CD2BD2，则BCD 为直角三角形， 四边形 ABCD 的面积BCCD+ABOC3+439； （3）存在，理由： 作点 C 关于 x 轴的对称点 E（0，3） ，连接 DE 交 x 轴于点 Q，则点 Q 为所求点， 设直线 ED 的表达式为 ykx+b，则，解得， 故直线 DE 的表达式为 y7x3， 令 y7x30，解得 x， 故点 Q 的坐标为（，0） 12解： （1）将点 A、C 的坐标代入抛物线表达式得，解得， 故抛物线的表达式为 yx2+x+4； （2）在 OB 上取 OR
28、OA2， 则ACR2ACOPAB， 过点 A 作 AKCR 于点 K，设直线 AP 交 y 轴于点 H， 则 SACRARCOCRAK，即44AK， 解得 AK，则 sinACK，则 tanACKtanBAP， 在 RtAOH 中，OHAOtanBAP2， 由点 A、H 的坐标得，直线 AP 的表达式为 yx； 联立并解得 x， 故点 P 的横坐标为； （3）设点 E、F 的坐标分别为（m，m2+m+4） 、 （n，n2+n+4） ， 联立与 ykxk+2 并整理得：x2+（2k2）x（4+2k）0， 则 m+n22k，mn42k， 由抛物线的表达式知，点 D（1，） ， 由点 D、F 的坐标
29、得，直线 FD 的表达式为 y（n1）x+n+4， 当 xm 时，y（n1）m+n+4mn+（m+n）+4（42k）+（22k）+47， 故点 P 的坐标为（m，7） ， 则 PC3， 故 PC 的最小值为 3 13解： （1）CO4，故 c4，则抛物线的表达式为 yax24， OC2OA4，故点 A（2，0） ，则 04a4，解得 a1， 故抛物线的表达式为 yx24； （2）过点 A 作 x 轴的垂线交 BP 的延长线于点 Q， 在BAQ 和COA 中， ， BAQCOA（AAS） ， AQOA2， Q（2，2） ， 由点 B、Q 的坐标得，直线 BQ 解析式为 yx1， 联立， 解得 x
30、12（舍去） ，x2， P（，） ； （3）设 E（x1，x124） ，F（x2，x224） ，P（1，3） ， 由点 P、E 的坐标得，yPE（x1+1）x4x1， 同理可得 yPF（x2+1）x4x2， 又PEPF， （x1+1） （x2+1）1， x1x2+x1+x2+11， x1x22（x1+x2） ， 同理可得 EF 的解析式为：yEF（x1+x2）x4x1x2， yEF（x1+x2）x4+2+（x1+x2）（x1+x2） （x+1）2， 直线 EF 恒过定点（1，2） ，设该点为 R， 连接点 AR，则 AR 为点 A 到直线 EF 距离的最大值， AR 14解： （1）对于，令
31、y（x+5） （xm）0，解得 x5 或 m，令 x 0，则 y（0+5） （0m）， 故点 A、B、C 的坐标分别为（5，0） 、 （m，0） 、 （0，） ， 当 m1 时，点 B 的坐标为（1，0） ； （2）由（1）知，点 B、C 的坐标为（m，0） 、 （0，） ； （3）依题意得 A（5，0） ，C（0，m） ， 由 m0，设过 A，C 两点的一次函数解析式是 ykx+b， 将 A，C 代入上式得，解得， 过 A，C 两点的一次函数解析式是 ymx+m， 设点 P（t，0） ，则5tm（m0） ， M（t，t2+t+） ，点 N（t，mt+） ， 当5t0 时， MN（t2+t+）
32、（mt+）t2t， 0， 该二次函数图象开口向下， 又对称轴是直线 t， 当 t时，MN 的长最大， 此时 MN（）2（）； 当 0tm 时， MN（mt+）（t2+t+）t2+t， 0， 该二次函数图象开口向上， 又对称轴是直线 t， 当 0tm 时，MN 的长随 t 的增大而增大， 当 tm 时，MN 的长最大，此时 MNm2+2.5m， 线段 MN 长的最大值为， m2+2.5m， 整理得： （m+2.5）2， 由图象可得：m， m0， m 的取值范围是 0m 15解： （1）yx22mx4m+4x22m（x+2）+4， 当 x2 时，y6， 抛物线 yx22mx4m+4 经过定点（2，
33、6） ， A（2，6） ； （2）yt（t6） ， x22mx4m+4t， x24mx8m+82t0， xB+xC4m，xBxC88m2t， DACABD，ADB90， ADBCBA， ， AD2BDCD， （6t）2（xB+2） （xC+2） ， 3612t+t2xBxC+2（xB+xC）+4， 3612t+t288m2t+8m+4， 整理得 t210t+240， 解得 t4 或 t6（舍去） ， t4； （3）存在，理由如下， 当 m1 时，抛物线为 yx22x， yx22x（x2）22， 对称轴为直线 x2， 直线 y2x 交对称轴于点 E， E（2，4） ， 过 E 点作 EFOE，E
34、Hy 轴，交 OP 于 F，交 y 轴于 H，作 FGEH 于 G， OH4，EH2， tanEOP， ， OEF90， HEO+GEF90GEF+GFE， HEOGFE， EHOFGE90， EOHFEG， ， EG2，FG1， F（4，3） ， 直线 OP 的解析式为 yx， 解得或， P（，） ， E（2，4） ， E 点关于 x 轴的对称点 E（2，4） ，连接 PE，交 x 轴于 M，此时 ME+MPPE，EM+PM 的值 最小， 设直线 PE的解析式为 ykx+b， ，解得 k，b， 直线 PE的解析式为 yx， 令 y0，则x+0， 解得 x， M（，0） ， t 16解： （1
35、）OA1，tanOAC3， 则 OCOAtanOAC3，故点 A、C 的坐标分别为（1，0） 、 （0，3） ， （2）抛物线 yx2+bx+c 经过点 A（1，0） ，C（0，3） ， ，解得， 抛物线的函数表达式为 yx2+2x3； 若点 P 在 x 轴下方，如图 1， 延长 AP 到 H，使 AHAB，过点 B 作 BIx 轴，连接 BH，作 BH 中点 G，连接并延长 AG 交 BI 于点 F， 过点 H 作 HIBI 于点 I， 当 x2+2x30，解得：x13，x21， B（3，0） ， A（1，0） ，C（0，3） ， OA1，OC3，AC，AB4， RtAOC 中，sinACO
36、，cosACO， ABAH，G 为 BH 中点， AGBH，BGGH， BAGHAG，即PAB2BAG， PAB2ACO， BAGACO， RtABG 中，AGB90，sinBAG， BGAB， BH2BG， HBI+ABGABG+BAG90， HBIBAGACO， RtBHI 中，BIH90，sinHBI，cosHBI， HIBH，BIBH， xH3+，yH，即 H（，） ， 由点 A、H 的坐标的，直线 AH 的表达式为：yx， 故直线 PA 在与 y 轴交点的坐标为（0，） ； 若点 P 在 x 轴上方，如图 2， 在 AP 上截取 AHAH，则 H与 H 关于 x 轴对称， H（，） ， 同理可得，直线 AH：yx+， 故直线 PA 在与 y 轴交点的坐标（0，） ； 综上，直线 PA 在与 y 轴交点的坐标为（0，）或（0，） ； （3）DM+DN 为定值， 抛物线 yx2+2x3 的对称轴为：直线 x1， D（1，0） ，xMxN1， 设 Q（t，t2+2t3） （3t1） ， 由点 A、Q 的坐标得，直线 AQ：y（t+3）xt3， 当 x1 时，yMt3t32t6， DM0（2t6）2t+6， 同理可得，直线 BQ：y（t1）x+3t3， 当 x1 时，yNt+1+3t32t2， DN0（2t2）2t+2， DM+DN2t+6+（2t+2）8，为定值
