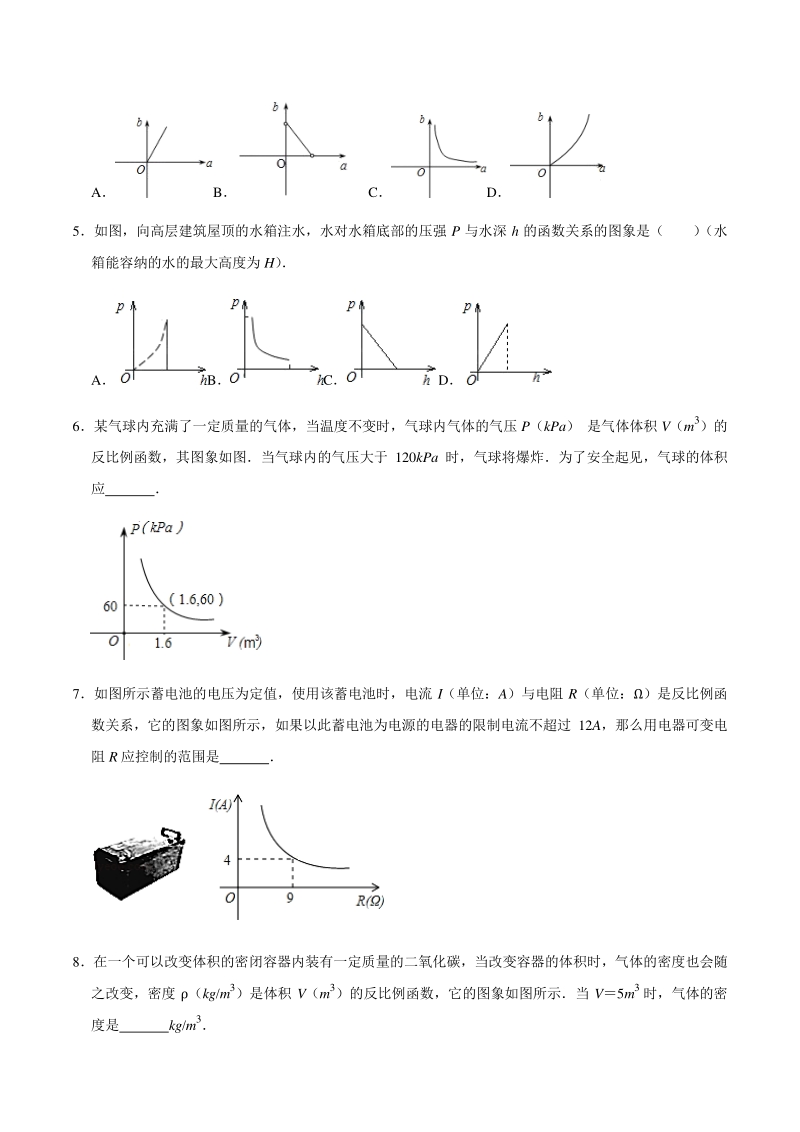
1、2021 年中考数学一轮复习专题突破训练：反比例函数的应用年中考数学一轮复习专题突破训练：反比例函数的应用 1某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强 p（Pa）是气球体积 V（m3） 的反比例函数，且当 V1.5m3时，p16000Pa，当气球内的气压大于 40000Pa 时，气球将爆炸，为确 保气球不爆炸，气球的体积应（ ） A不小于 0.5m3 B不大于 0.5m3 C不小于 0.6m3 D不大于 0.6m3 2小颖和小亮玩掷骰子游戏，每人分别先后掷两次得到 a，b，并约定点（a，b）落在如图反比例函数 y （x0）图象内为小亮胜，落在外则小颖胜，落在图象上为平
2、局，你认为谁获胜希望较大？（ ） A小颖 B小亮 C都一样 D无法确定 3 如图， 反比例函数的一个分支与O 有两个交点 A， B， 且这个分支平分O， 以下说法正确的是 （ ） A反比例函数的这个分支必过圆心 O B劣弧 AB 等于 120 度 C反比例函数的这个分支把O 的面积平分 D反比例函数的这个分支把O 的周长平分 4 已知有一根长为 10 的铁丝， 折成了一个矩形框 则这个矩形相邻两边 a， b 之间函数的图象大致为 （ ） AB CD 5如图，向高层建筑屋顶的水箱注水，水对水箱底部的压强 P 与水深 h 的函数关系的图象是（ ） （水 箱能容纳的水的最大高度为 H） ABCD 6
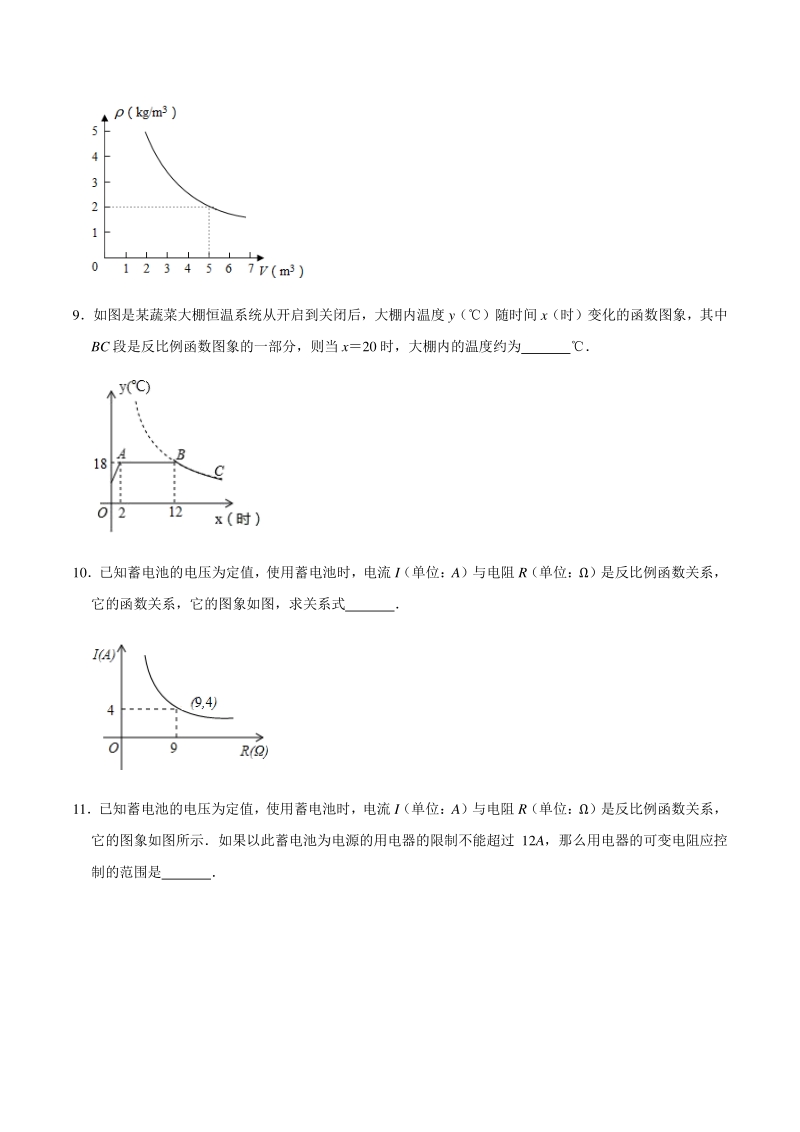
3、某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 P（kPa） 是气体体积 V（m3）的 反比例函数，其图象如图当气球内的气压大于 120kPa 时，气球将爆炸为了安全起见，气球的体积 应 7如图所示蓄电池的电压为定值，使用该蓄电池时，电流 I（单位：A）与电阻 R（单位：）是反比例函 数关系，它的图象如图所示，如果以此蓄电池为电源的电器的限制电流不超过 12A，那么用电器可变电 阻 R 应控制的范围是 8在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随 之改变，密度 （kg/m3）是体积 V（m3）的反比例函数，它的图象如图所示当 V5m
4、3时，气体的密 度是 kg/m3 9如图是某蔬菜大棚恒温系统从开启到关闭后，大棚内温度 y（）随时间 x（时）变化的函数图象，其中 BC 段是反比例函数图象的一部分，则当 x20 时，大棚内的温度约为 10已知蓄电池的电压为定值，使用蓄电池时，电流 I（单位：A）与电阻 R（单位：）是反比例函数关系， 它的函数关系，它的图象如图，求关系式 11已知蓄电池的电压为定值，使用蓄电池时，电流 I（单位：A）与电阻 R（单位：）是反比例函数关系， 它的图象如图所示如果以此蓄电池为电源的用电器的限制不能超过 12A，那么用电器的可变电阻应控 制的范围是 12在温度不变的条件下，一定质量的气体的压强 P
5、与它的体积 V 成反比例，当 V200 时，P50，则当 P25 时，V 13小伟欲用撬棍撬动一块大石头，已知阻力和阻力臂分别为 1200N 和 0.5m，当撬动石头的动力 F 至少需 要 400N 时，则动力臂 l 的最大值为 m 14由 x 人完成报酬共为 100 元的某项任务，若人均报酬 y 元不少于 24 元，且 y 为整数，则完成此任务的 人数 x 的值为 15我们已经学习了反比例函数，在生活中，两个变量间具有反比例函数关系的实例有许多，例如：在路 程 s 一定时，平均速度 v 是运行时间 t 的反比例函数，其函数关系式可以写为：v （s 为常数，s0） 请你仿照上例，再举一个在日常
6、生活、学习中，两个变量间具有反比例函数关系的实例： ；并写 出这两个变量之间的函数解析式： 16实验数据显示：一般成年人喝半斤低度白酒后，1.5 小时内其血液中酒精含量 y（毫克/百毫升）与时间 x（时）的关系可近似地用二次函数 yax2+bx 刻画；1.5 小时后（包括 1.5 小时）y 与 x 可近似地用反比 例函数 y（k0）刻画如图所示，并且通过测试发现酒后半小时和 1.5 小时的酒精含量均为 150 毫 克/百毫升，酒后 5 小时为 45 毫克/百毫升 （1）求二次函数和反比例函数解析式； （2）喝酒后几时血液中的酒精含量达到最大值？最大值为多少？ （3）按国家规定：车辆驾驶人员血液
7、中的酒精含量大于或等于 20 毫克/百毫升时属于“酒后驾驶” ，不 能驾驶上路参照上述数学模型，假设某驾驶员晚上 20：00 在家喝完半斤低度白酒，第二天早上 8：00 能否驾车去上班？请说明理由 17 某医药研究所研发了一种新药， 试验药效时发现： 1.5 小时内， 血液中含药量 y （微克） 与时间 x （小时） 的关系可近似地用二次函数 yax2+bx 表示；1.5 小时后（包括 1.5 小时） ，y 与 x 可近似地用反比例函数 y（k0）表示，部分实验数据如表： 时间 x（小时） 0.2 1 1.8 含药量 y（微克） 7.2 20 12.5 （1）求 a、b 及 k 的值； （2）
8、服药后几小时血液中的含药量达到最大值？最大值为多少？ （3）如果每毫升血液中含药量不少于 10 微克时治疗疾病有效，那么成人按规定剂量服用该药一次后能 维持多长的有效时间 （1.41，精确到 0.1 小时） 18 某商场出售一批进价为 2 元的贺卡，在市场营销中发现此商品的日销售单价 x （元）与日销售量 y （个） 之间有如下关系： 日销售单价 x （元） 3 4 5 6 日销售量 y（个） 20 15 12 10 （1）猜测并确定 y 与 x 之间的函数关系式，并画出图象； （2）设经营此贺卡的销售利润为 W 元，求出 W 与 x 之间的函数关系式， （3）若物价局规定此贺卡的售价最高不能
9、超过 10 元/个，请你求出当日销售单价 x 定为多少时，才能获 得最大日销售利润？最大利润是多少元？ 19 货轮从甲港往乙港运送货物， 甲港的装货速度是每小时 30 吨， 一共装了 8 小时， 到达乙港后开始卸货， 乙港卸货的速度是每小时 x 吨，设卸货的时间是 y 小时， （1）求 y 与 x 间的函数关系式； （2）若卸货的速度是 40 吨每小时，求乙港的卸完全部货物的时间是多少？ （3）在（2）的条件下，当卸货时间在 4 小时的时候，问船上剩余货物是多少吨？ 20 某医药研究所研制并生产治疗同种病的 A、 B 两种新药， 经过统计， 有两个成年人同时按正常药量服用， 1 小时后， 服用
10、 A 药品的血液中含药量 y1（微克/毫升） 与时间 x （小时） 满足反比例函数 y1 （x1） ， 服用 B 药品的血液中含药量 y2（微克/毫升）与时间 x（小时）满足二次函数 y2ax2+bx+c（x1） ，如图 所示，且在 3 小时，含药量达到最大值为 8 微克/毫升， （1）求 k 以及 a、b、c 的值； （2）当服用 B 药品的血液中含药量 y2为 3.5 微克/毫升时，求 y1的值； （3）若血液中 B 药品含药量不低于 6.5 微克/毫升时，A 药品含药量在 0.75 微克/毫升与 4.5 微克/毫升之 间（包括 0.75 和 4.5）时为疗效时间，求这两种药品均起疗效的时
11、间有多长？（结果保留根号） 21已知某电路的电压 U（V） ，电流 I（A） ，电阻 R（）三者之间有关系式 UIR，且电路的电压 U 恒为 220V （1）求出电流 I 关于电阻 R 的函数表达式； （2）如果该电路的电阻为 250，则通过它的电流是多少？ （3）如图，怎样调整电阻箱 R 的值，可以使电路中的电流 I 增大？若电流 I1.1A，求电阻 R 的值 22春季是流感高发的季节，为此，某校为预防流感，对教室进行熏药消毒在对教室进行消毒的过程中， 先经过 10min 的药物燃烧， 再封闭教室 15min， 然后打开门窗进行通风 已知室内空气中含药量 y （mg/m3） 与药物在空气中的
12、持续时间 x（min）之间的函数关系式如图所示（即图中线段 OA、线段 AB 和双曲线在 点 B 及其右侧部分） ，请根据图中信息解答下列问题： （1）求药物燃烧阶段和打开门窗进行通风阶段 y 与 x 之间的函数表达式； （2）若室内空气中的含药量不低于 5mg/m3且持续时间不少于 35min，才能有效消灭病毒，则此次消毒 是否有效？请说明理由 23阅读下列材料： 对于任意正实数 a，b，0，a2+b0，a+b2，当且仅当 ab 时，等号 成立 结论：在 a+b2均为正实数）中，若 ab 为定值 p，则 a+b2，当且仅当 ab 时，a+b 有最小值 2 拓展：对于任意正实数 a，b，c，都
13、有 a+b+c3，当且仅当 abc 时，等号成立在 a+b+c 3， （a，b，c 均为正实数）中，若 abc 为定值 p，则 a+b+c3，当且仅当 abc 时，a+b+c 有最小值 3 例如：x0，则 x+4，当且仅当 x，即 x2 时等号成立又如：若 x0，求 2x+的 最小值时，因为 2x+6，当且仅当 x，即 x2 时等号成立，故当 x 2 时，2x+有最小值 6根据上述材料，解答下列问题： （1）若 a 为正数，则当 a 时，代数式 2a+取得最小值，最小值为 ； （2）已知函数 y1x2（x0）与函数 y2，求函数 y1+y2的最小值及此时 x 的值； （3）我国某大型空载机的一
14、次空载运输成本包含三部分：一是基本运输费用，共 8100 元；二是飞行耗 油，每一百公里 1200 元；三是飞行损耗费用，飞行损耗费用与路程（单位：百公里）的平方成正比，比 例系数为 0.04，设该空载机的运输路程为 x 百公里，则该空载机平均每一百公里的运输成本 y 最低为多 少？ 24某月食品加工厂以 2 万元引进一条新的生产加工线已知加工这种食品的成本价每袋 20 元，物价部门 规定：该食品的市场销售价不得高于每袋 35 元，若该食品的月销售量 y（千袋）与销售单价 x（元）之 间的函数关系为：y（月获利月销售收入生产成本投资成本） （1）当销售单价定为 25 元时，该食品加工厂的月销量
15、为多少千袋； （2）求该加工厂的月获利 M（千元）与销售单价 x（元）之间的函数关系式； （3）求销售单价范围在 30 x35 时，该加工厂是盈利还是亏损？若盈利，求出最大利润；若亏损，最 小亏损是多少 25 保护生态环境， 建设绿色社会已经从理念变为人们的行动 某化工厂 2009 年 1 月的利润为 200 万元 设 2009 年 1 月为第 1 个月，第 x 个月的利润为 y 万元由于排污超标，该厂决定从 2009 年 1 月底起适当 限产，并投入资金进行治污改造，导致月利润明显下降，从 1 月到 5 月，y 与 x 成反比例到 5 月底， 治污改造工程顺利完工，从这时起，该厂每月的利润比
16、前一个月增加 20 万元（如图） （1）分别求该化工厂治污期间 y 与 x 之间对应的函数关系式 （2）求 5 月份的利润及治污改造工程完工后 y 与 x 之间对应的函数关系式 （3）治污改造工程完工后经过几个月，该厂月利润才能达到 2009 年 1 月的水平？ 参考答案参考答案 1解：设函数解析式为 P， 当 V1.5m3时，p16000Pa， kVp24000， p， 气球内的气压大于 40000Pa 时，气球将爆炸， 40000， 解得：V0.6，即气球的体积应不小于 0.6m3 故选：C 2解：列表如下： 1 2 3 4 5 6 1 （1，1） （2，1） （3，1） （4，1） （5
17、，1） （6，1） 2 （1，2） （2，2） （3，2） （4，2） （5，2） （6，2） 3 （1，3） （2，3） （3，3） （4，3） （5，3） （6，3） 4 （1，4） （2，4） （3，4） （4，4） （5，4） （6，4） 5 （1，5） （2，5） （3，5） （4，5） （5，5） （6，5） 6 （1，6） （2，6） （3，6） （4，6） （5，6） （6，6） 所有等可能的情况，即 P 坐标有 36 种，落在数 y（x0）图象内部有 13 种情形，落在外部有 19 种情形， 小亮胜的概率，小颖胜的概率为， 小颖胜的可能性比较大， 故选：A 3解：A、反比例函
18、数的这个分支不可能过圆心 O，否则无法平分圆，故错误； B、劣弧 AB 等于 180，故错误； C、反比例函数的这个分支不能把O 的面积平分，故错误； D、这个分支平分O，即反比例函数的这个分支把O 的周长平分，D 正确 故选：D 4解：根据题意有：a+b5； 故 a 与 b 之间的函数图象为一次函数，且根据实际意义 a、b 应大于 0其图象在第一象限； 故选：B 5解：P 与水深 h 的函数关系为 Pgh，即压强 P 与水深 h 成正比 故选：D 6解：设球内气体的气压 P（kPa）和气体体积 V（m3）的关系式为 P， 图象过点（1.6，60） k96 即 P在第一象限内，P 随 V 的增
19、大而减小， 当 P120 时，V 故答案为：不小于m3 7解：设电流 I 与电阻 R 的函数关系式为 I， 图象经过的点（9，4） ， k36， I， 电流不超过 12A， 12， 解得：R3， 故答案为：R3 8解：由图象可知，函数图象经过点（5，2） ， 所以当 V5m3时，气体的密度是 2kg/m3 故答案为 2 9解：点 B（12，18）在双曲线 y上， 18， 解得：k216 当 x20 时，y10.8， 所以当 x20 时，大棚内的温度约为 10.8 故答案为：10.8 10解：电流 I 是电阻 R 的反比例函数，设 I， 图象经过（9，4） ， 4， 解得 k4936， I， 故
20、答案为：I 11解：由题意可得：I，将（9，4）代入得： UIR36， 以此蓄电池为电源的用电器的限制不能超过 12A， 12， 解得：R3 故答案为：R3 12解：一定质量的气体的压强 P 与它的体积 V 成反比例，当 V200 时，P50， KPV10000， 当 P25 时，V1000025400 故答案为：400 13解：由杠杆平衡条件可知：动力动力臂阻力阻力臂， 即：400l12000.5， 解得 l1.5 故答案为：1.5 14解：由 x 人完成报酬共为 100 元的某项任务， xy100， 即：y， 人均报酬 y 元不少于 24 元，且 y 为整数， x1、2、4 故答案为：1、
21、2、4 15解：矩形的面积 S 一定时，矩形的长 a 是矩形的宽 b 的反比例函数， 这两个变量之间的函数解析式为：a（S 为常数，且 S0） 故答案为：矩形的面积 S 一定时，矩形的长 a 是矩形的宽 b 的反比例函数；a （S 为常数，且 S0） 16解： （1）根据题意： 酒后半小时和 1.5 小时的酒精含量均为 150 毫克/百毫升， 即当 x0.5 时，y150，x1.5 时，y150 1.5 小时内其血液中酒精含量 y（毫克/百毫升）与时间 x（时）的关系可近似地用二次函数 yax2+bx 刻画， 即当 0 x1.5 时，yax2+bx， 解得 所以二次函数解析式为 y200 x2
22、+400 x（0 x1.5） ； 酒后 5 小时为 45 毫克/百毫升 1.5 小时以后（包括 1.5 小时）y 与 x 可近似地用反比例函数 y（k0）刻画， 即当 x5 时，y45， k545225， 所以反比例函数解析式为 y（x1.5） 答：二次函数解析式为 y200 x2+400 x（0 x1.5） ； 反比例函数解析式为 y（x1.5） （2）二次函数解析式为 y200 x2+400 x， y200 x2+400 x200（x1）2+200， 当 x1 时，血液中的酒精含量达到最大值，最大值为 200（毫克/百毫升） ； （3）第二天早上 8：00 能驾车去上班，理由如下： 晚上
23、20：00 在家喝完半斤低度白酒，第二天早上 8：00，一共 12 个小时， 将 x12 代入 y， 则 y20， 答：第二天早上 8：00 能驾车去上班 17解： （1）设 1.5 小时内，血液中含药量 y（微克）与时间 x（小时）的关系为 yax2+bx， 根据表格得：， 解得：a20，b40， 1.5 小时后（包括 1.5 小时） ，y 与 x 可近似地用反比例函数 y（k0） ，根据表格得： k1.812.522.5， a20，b40，k22.5； （2）由（1）知 y20 x2+40 x， y20（x1）2+20， 服药后 1 小时血液中的含药量达到最大值，最大值为 20 微克； （
24、3）当 y10 时，1020 x2+40 x，或 10， 解得：x1或 x1+，x2.25， 成人按规定剂量服用该药一次后能维持 2.25（1）2.0 小时的有效时间 18解： （1）由表可知，xy60， y （x0） ， 函数图象如下： （2）根据题意，得： W（x2） y （x2） 60； （3）x10， 12， 则 6048， 即当 x10 时，W 取得最大值，最大值为 48 元， 答：当日销售单价 x 定为 10 元/个时，才能获得最大日销售利润，最大利润是 48 元 19解： （1）总货量308240 吨， xy240， 故 y （2）x40，代入 y可得 y6， 乙港的卸完全部货物
25、的时间是 6 小时 （3）x40， 即当卸货时间在 4 小时的时候共卸货 440160 吨 船上剩余货物是 24016080 吨 20解： （1）把（1，6）代入 y1得，k166， 在 3 小时，含药量达到最大值为 8 微克/毫升， 设 y2（微克/毫升）与时间 x（小时）满足二次函数关系式为 y2a（x3）2+8， 把（1，6）代入得，6a（13）2+8， 解得：a， y2（微克/毫升）与时间 x（小时）满足二次函数关系式为 y2（x3）2+8， 即 y2（x3）2+8x2+3x+， b3，c； （2）把 y23.5 代入 y2x2+3x+得， 3.5x2+3x+， 解得：x10，x26，
26、 把 x6 代入 y1得 y11； （3）如果每毫升血液中含药量不低于 6.5 微克时为疗效时间， y6.5 时，6.5x2+3x+， 解得：x13+，x23， 把 y0.75 和 4.5 分别代入 y1得，x8，x， 这两种药品均起疗效的时间有（3+）小时 21解： （1）某电路的电压 U（V） ，电流 I（A） ，电阻 R（）三者之间有关系式 UIR， I， 代入 U220 得：I， 电流 I 关于电阻 R 的函数表达式是 I； （2）当 R250 时，I0.88A， 电路的电阻为 250，则通过它的电流是 0.88A； （3）I， 电流与电阻成反比关系， 要使电路中的电流 I 增大可以减
27、少电阻， 当 I1.1A 时，I1.1A， 解得：R200 22解： （1）设正比例函数的解析式为 ykx， 把（8，12） ）代入解析式得，k， 则正函数解析式为 yx（0 x10） ， 将 x10 代入解析式得，y15， 故 A（10，15） ， 设反比例函数解析式为 y， 将（25，8）代入解析式得，k258200， 则反函数解析式为 y（x25） ， （2）将 y5 代入 yx 得 x， 将 y5 代入 yx 得到 x40， 4035， 这次消毒很彻底 23解： （1）因为 2a+22，当且仅当 2a，即 a时等号成立，故当 a时，2a+ 取得最小值为 2； 故答案为：，2； （2）y
28、1x2（x0） ，y2， 函数 y1+y2x2+， x2+x2+312，当且仅当 x2，即 x2 时等号成立，故当 x2 时，x2+ 取得最小值是 12， 即函数 y1+y2的最小值是 12，此时 x 的值是 2； （3）设该空载机的运输路程为 x 百公里，则运输成本为 xy 元， 由题意得：xy8100+1200 x+0.04x2， y， 因为+0.04x236，当且仅当，即 x450 时等号成立， y36+12001236， 故该空载机平均每一百公里的运输成本 y 最低为 1236 元 24解： （1）当 x25 时，y24 千袋， 所以当销售单价定为 25 元时，该食品加工厂的月销量为
29、24 千袋； （2）当 20 x30 时，M（x20）20580； 当 30 x35 时，M（0.5x+10） （x20）20 x2220； （3）当 30 x35 时，Mx2220，当 x35 时，M 最大，则 M352220392.5（千元） 39.25（万元） ， 答：此时该加工厂盈利，最大利润为：39.25 万元 25解： （1）当 1x5 时，设，把（1，200）代入，得 k200，即； （2）从 1 月到 5 月，y 与 x 成反比例 当 x5 时，即， y40， 到 5 月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加 20 万元， 当 x5 时，y40+20（x5）20 x60； （3）当 y200 时，20 x60200， 解得：x13， 所以治污改造工程顺利完工后经过 1358 个月后，该厂利润达到 200 万元
