1、太原太原 2020-2021 学年第一学期九年级期末考试数学模拟试卷学年第一学期九年级期末考试数学模拟试卷 一、选择题（本大题共一、选择题（本大题共 10 道小题，每小题道小题，每小题 3 分，共分，共 30分）分） 1. 方程 2 80 x 的解为（ ） A. 1 4x ， 2 4x B. 1 2 2x ， 2 2 2x C. 1 0 x ， 2 2 2x D. 2 2x 【答案】B 2. 下列函数中，y是 x 的反比例函数的是（ ） A. x y 3 B. 5 y x C. 2 1 y x D. 1 y2 x 【答案】B 3. 如图所示的几何体的俯视图是（ ） A. B. C. D. 【答
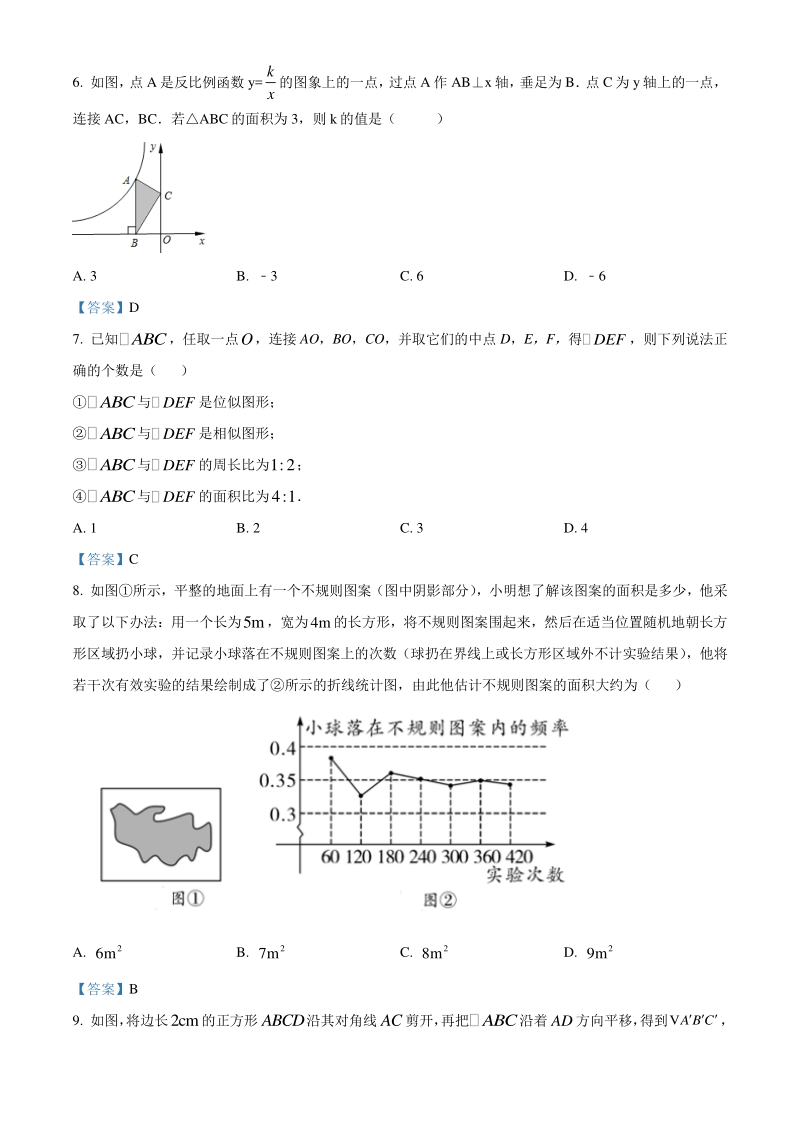
2、案】B 4. 如图所示，在平行四边形 ABCD 中，对角线 AC、BD 相交于点 O，下列条件不能判定平行四边形 ABCD 为矩形是（） A. ABC90 B. ACBD C. AD=AB D. BADADC 【答案】C 5. 经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，则两辆汽车 经过这个十字路口时，一辆向右转，一辆向左转的概率是( ) A. 2 3 B. 2 9 C. 1 3 D. 1 9 【答案】B 6. 如图， 点 A是反比例函数 y= k x 的图象上的一点， 过点 A 作 ABx轴， 垂足为 B 点 C为 y轴上的一点， 连接 AC，BC若ABC
3、的面积为 3，则 k的值是（ ） A. 3 B. 3 C. 6 D. 6 【答案】D 7. 已知ABC，任取一点O，连接 AO，BO，CO，并取它们的中点 D，E，F，得 DEF，则下列说法正 确的个数是（ ） ABC与DEF是位似图形； ABC与DEF是相似图形； ABC与DEF的周长比为1:2； ABC与DEF的面积比为4:1 A. 1 B. 2 C. 3 D. 4 【答案】C 8. 如图所示，平整的地面上有一个不规则图案（图中阴影部分） ，小明想了解该图案的面积是多少，他采 取了以下办法：用一个长为5m，宽为4m的长方形，将不规则图案围起来，然后在适当位置随机地朝长方 形区域扔小球，并记
4、录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果） ，他将 若干次有效实验的结果绘制成了所示的折线统计图，由此他估计不规则图案的面积大约为（ ） A. 2 6m B. 2 7m C. 2 8m D. 2 9m 【答案】B 9. 如图， 将边长2cm的正方形ABCD沿其对角线AC剪开， 再把ABC沿着AD方向平移， 得到 A B C V， 若两个三角形重叠部分的面积为 2 1cm，则它移动的距离 AA 等于（ ） A. 0.5cm B. 1cm C. 1.5cm D. 2cm 【答案】B 10. 如图，ABC 中，D、E 是 BC 边上的点，BD：DE：EC=3：2：1，M
5、在 AC 边上，CM：MA=1：2，BM 交 AD， AE 于 H，G，则 BH：HG：GM 等于（ ） A. 3：2：1 B. 5：3：1 C. 25：12：5 D. 51：24：10 【答案】D 二、填空题（本大题共二、填空题（本大题共 5 道小题，共道小题，共 10 分）分） 11. 若关于 x的方程 2 20 xxm有两个相等的实数根，则实数 m的值等于_ 【答案】 1 8 12. 在函数 4 y x 的图象上有三点 （3， y1） 、 （2， y2） 、 （1， y3） ， 则函数值 y1、 y2、 y3的大小关系为_ 【答案】y3y1y2 13. 如图，平面内直线 1234 / /
6、 /llll，且相邻两条平行线间隔均为 1，正方形ABCD四个顶点分别在四条平 行线上，则正方形的面积为_ 【答案】5 14. 如图，在RtABC中，90ACB，12AC ，24BC ，点 D在边BC上，点 E在线段AD上， EFAC于点 F，EGEF交AB于点 G若EFEG，则CD的长为_ 【答案】8 15. 如图,菱形 ABCD顶点 A 在例函数 y= 3 x (x0)的图象上，函数 y= k x (k3，x0)的图象关于直线 AC 对称， 且经过点 B、D两点，若 AB2，DAB30 ，则 k的值为_. 【答案】6+2 3 三、解答题（本大题共三、解答题（本大题共 8 道小题，共道小题，
7、共 60 分）分） 16. 解下列过程： （1） 2 220 xx； （2）(23)(32)(23)xxxx 【答案】 （1） 1 13x ， 2 13x ； （2） 1 1.5x ， 2 1x 17. 共享经济已经进入人们的生活小沈收集了自已感兴趣的 4个共享经济领域的图标，共享出行、共享服 务、共享物品、共享知识，制成编号为 A、B、C、D的四张卡片（除字母和内容外，其余完全相同） 现将 这四张卡片背面朝上，洗匀放好 （1）小沈从中随机抽取一张卡片是“共享服务”的概率是 ； （2）小沈从中随机抽取一张卡片（不放回） ，再从余下的卡片中随机抽取一张，请你用列表或画树状图的 方法求抽到的两张卡
8、片恰好是“共享出行”和“共享知识”的概率 （这四张卡片分别用它们的编号 A、 B、 C、D表示） 【答案】 （1） 1 4 ； （2） 1 6 18. 在大棚中栽培新品种的蘑菇，在18的条件下生长最快，因此用装有恒温系统的大棚栽培，如图是某 天恒温系统从开启升温到保持恒温及关闭大棚内温度 y（）随时间 x（时）变化的函数图象，其中BC 段是函数 k y x （0k ）图象的一部分 （1）求出当12x时对应的 y与 x 的函数关系式； （2）若该蘑菇适宜生长的温度不低于12，则这天该种蘑菇适宜生长的时间是多长？ 【答案】 （1） 216 y x (12x)； （2）17.5小时 19. 如图，是
9、两棵树分别在同一时刻、同一路灯下的影子 （1）请画出路灯灯泡的位置（用字母O表示） （2）在图中画出路灯灯杆（用线段OC表示） ； （3）若左边树AB的高度是 4米，影长是 3米，树根B离灯杆底的距离是 1米，求灯杆的高度 【答案】 （1）见解析； （2）见解析； （3）灯杆高度是 16 3 米 20. 如图，ABC中，ABAC，AD是BC边上的高，点 O是AC中点，延长DO到 E，使OE OD=， 连接AE，CE 求证：四边形ADCE是矩形 【答案】见解析 21. 如图，某小区规划在一个长30m，宽20m矩形场地上，修建两横两竖四条同样宽的道路，且横、竖 道路分别与矩形的长、 宽平行， 其余
10、部分种草坪， 若使每块草坪的面积都为 2 56m.应如何设计道路的宽度？ 【答案】道路的宽度应设计为 1m. 22. 综合与实践四边形旋转中的数学 “智慧”数学小组在课外数学活动中研究了一个问题，请帮他们解答 问题情境： 如图 1， 在矩形ABCD中，AB6，8AD ， E， F分别为AB，AD边的中点， 四边形AEGF 为矩形，连接CG 特例分析： （1）请直接写出CG的长是_ （2）如图 2，当矩形AEGF绕点 A 旋转（比如顺时针旋转）至点 G落在边AB上时，请计算DF与CG的 长，通过计算，试猜想DF与CG之间的数量关系 深入探究： （3）请从下面 A、B 两题中任选一题作答我选择_题
11、 A当矩形AEGF绕点 A 旋转至如图 3 的位置时， （2）中DF与CG之间的数量关系是否还成立？请说明 理由 B “智慧”数学小组对图形的旋转进行了拓展研究， 如图 4， 在A B C D中，60B ，AB6，8AD ， E，F 分别为AB，AD边的中点，四边形AEGF为平行四边形，连接CG“智慧”数学小组发现DF与 CG仍然存在着特定的数量关系 如图 5， 当A E G F绕点 A旋转 （比如顺时针旋转） ， 其他条件不变时，DF 与CG是否还存在着第（2）问中特定的数量关系？请说明理由 【答案】 （1）5； （2） 4 5 DFCG； （3）A成立，理由见解析；B存，理由见解析 23.
12、 如图，在同一平面直角坐标系中，直线2yx和双曲线 8 y x 相交于 A、B两点 （1）连结AO、BO，求出AOB面积 （2）已知点 E 在双曲线 8 y x 上且横坐标为 1，作EF垂直于 x轴垂足为 F，点 H 是 x 轴上一点，连结EH 交双曲线于点 I，连结IF并延长交 y 轴于点 G，若点 G坐标为 8 0, 5 ，请求出 H 点的坐标 （3）已知点 M 在 x 轴上，点 N 是平面内一点，以点 O、E、M、N为顶点的四边形是菱形，请你直接写出 N 点的坐标 【答案】 （1）6； （2） 213 ,0 2 H ； （3）(1, 8)或(165,8)或(165,8)或 63 (,8) 2
