1、第 1 页 共 4 页 x O y x O y x O y x O y 20202021 学年佛山市普通高中高三教学质量检测(一)学年佛山市普通高中高三教学质量检测(一) 数 学 数 学 注意事项注意事项: 1答卷前,考生要务必填涂答题卷上的有关项目 2选择题每小题选出答案后,用2B铅笔把答案涂在答题卷相应的位置上 3非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内；如需改动, 先划掉原来的答案,然后再写上新的答案；不准使用铅笔和涂改液,不按以上要求作答的答案无效 4请考生保持答题卷的整洁.考试结束后,将答题卷交回. 一、选择题一、选择题:本题共8小题,每小题5 分
2、,共40 分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1已知全集U为实数集, 2 30Ax xx = , 1Bx x = ,则 ( ) U AB = ? ( ) A 01xx B 01xx C 13xx ”是“2abc + ”的( ) A充分不必要条件B必要不充分条件 C充分必要条件D既不充分也不必要条件 4. 平行四边形ABCD中,点E是DC的中点,点F是BC的一个三等分点(靠近B),则EF ? ? ( ) A. 11 23 ABAD ? ? B. 11 42 ABAD + ? ? C. 11 32 ABAD + ? ? D. 12 23 ABAD ? ? 5. 随着新一轮科技
3、革命和产业变革持续推进,以数字化、网络化、智能化以及融合化为主要特征的新型基 础设施建设越来越受到关注.5G基站建设就是“新基建”的众多工程之一,截至2020年底,我国已累 计开通5G基站超70万个,未来将进一步完善基础网络体系,稳步推进5G网络建设,实现主要城区及 部分重点乡镇5G网络覆盖.2021年1月计划新建设5万个5G基站,以后每个月比上一个月多建设1万 个,预计我国累计开通500万个5G基站时要到( ) A.2022年12月B.2023年2月C.2023年4月D.2023年6月 6. 设sin2a = ,则( ) A. 2 1 2 2log a aa B. 2 1 2 log2 a
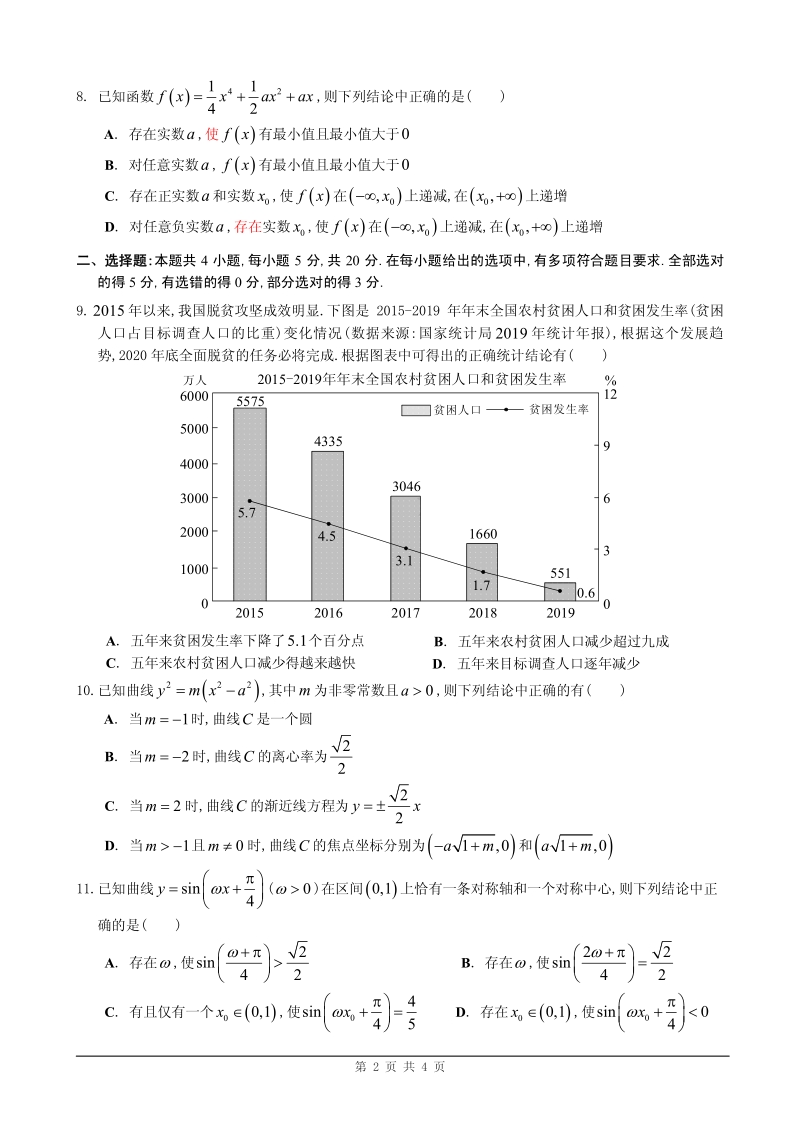
4、aa C. 2 1 2 log2 a aa D. 2 1 2 log2 a aa ,则下列结论中正确的有( ) A. 当1m = 时,曲线C是一个圆 B. 当2m = 时,曲线C的离心率为 2 2 C. 当2m = 时,曲线C的渐近线方程为 2 2 yx = D. 当1m 且0m 时,曲线C的焦点坐标分别为 ( ) 1,0am + 和 ( ) 1,0am + 11.已知曲线sin 4 yx =+ (0 )在区间( )0,1上恰有一条对称轴和一个对称中心,则下列结论中正 确的是( ) A. 存在 ,使 2 sin 42 + B. 存在 ,使 22 sin 42 + = C. 有且仅有一个 ( )
5、 0 0,1x ,使 0 4 sin 45 x += D. 存在 ( ) 0 0,1x ,使 0 sin0 4 x + )的焦点为F,准线l交x轴于点K,过F作倾斜角为 的直线与C 交于,A B两点,若60AKB =,则sin =_. 16.已知四棱锥PABCD 的顶点都在球O上,3AB = ,4BC = ,1CD = ,2 6AD = ,5AC = ,平面 PAD 平面ABCD,且PAPD ,则球O的体积为_. 四、解答题:四、解答题:本题共 6 小题,共 70 分,解答应写出文字说明、证明过程或演算步骤. 17.( (10 分)分) 在 212 loglog1 nn aa + =+ , 1
6、 2 n nn aa + =+ , 22 11 2 nnnn aaaa + = (0 n a )这三个条件中任选一个, 补充在下面问题中,并作答. 已知 nn ba 为等差数列, n b的前n项和为 n S,且 1 2a = , 1 2b = , 3 14b = ,_,是否存在 正整数k,使得2021 k S ?若存在,求k的最小值；若不存在,说明理由. 注:如果选择多个条件分别作答,按第一个解答计分. 18.( (12 分)分) 如图,在梯形ABCD中,/ /ABCD,2AB = ,5CD = , 2 3 ABC = . (1) 若2 7AC = ,求梯形ABCD的面积； (2) 若ACBD
7、 ,求tan ABD . 19.( (12 分)分) 如图,直三棱柱 111 ABCABC 中, 1 1 2 2 ACBCAA = ,M、N分别 为AB、 11 BC的中点. (1) 求证:/MN平面 11 ACC A； (2) 若 1 3 2B M = ,求二面角 11 BAMN 的余弦值. 第 4 页 共 4 页 区域IV区域III 区域II区域I 180 160 140 120 100 0 y(AQI) x(人数) 140130100110120708090605040 20 40 60 80 连续60天参加健身运动人数与AQI散点图 20.( (12 分)分) 为了了解空气质量指数(A
8、QI)与参加户外健身运动的人数之间的关系,某校环保小组在暑假期间(60 天)进行了一项统计活动:每天记录到体育公园参加户外健身运动的人数,并与当天 AQI 值(从气象部门获 取)构成60组成对数据( ), ii x y(1,2,60i = ? ),其中 i x为当天参加户外健身运动的人数, i y为当天的 AQI 值,并制作了如下散点图: (1) 环保小组准备做y与x的线性回归分析,算得y与x的相关系数为0.58 ,试分析y与x的线 性相关关系？ (2) 环保小组还发现散点有分区聚集的特点,尝试作聚类分析.用直线100 x = 与100y = 将散点图分 成、四个区域(如图),统计得到各区域的
9、点数分别为5、10、10、35,并初步认定“参加户 外健身运动的人数不少于100与AQI 值不大于100有关联”,试分析该初步认定的犯错率是否小于1%? 附: ( ) ( )( )( )( ) 2 2 n adbc K abcdacbd = + 21.( (12 分)分) 已知椭圆C: 22 22 1 xy ab += (0ab )的右焦点为 ( )1,0F,且过点 ( )2,0A . (1) 求C的方程； (2) 点P、Q分别在C和直线4x = 上,/OQAP,M为AP的中点,求证:直线OM与直线QF的交 点在某定曲线上. 22.( (12 分)分) 设0a 且1a ,函数 ( )sinsi
10、nfxaxax = . (1) 若 ( )fx在区间( )0,2 有唯一极值点 0 x,证明: ( ) ( ) 0 min 2, 1fxaa 得10n ,即存在正整数k,使得2021 k S ,且k的最小值为10.10 分 选: 由 1 2 n nn aa + =+ 得 1 21 2aa = , 2 32 2aa = , 3 43 2aa = , 1 1 2 n nn aa = (2n ), 1 分 相加得 ( ) 1 1231 1 2 12 222222 12 n nn n aa =+= ? ,又 1 2a = ,所以2 n n a = (2n ), 显然 1 2a = 也满足2 n n a
11、 = (2n ),故2 n n a = . 3 分 下同选. 选: 由 22 11 2 nnnn aaaa + = 整理得( )( ) 11 20 nnnn aaaa + += , 1 分 又0 n a ,所以 1 2 nn aa + = ,即 1 2 n n a a + = , 第 2 页 共 5 页 z y x O M C1 B1 A1 C B A N 所以 n a是首项为2,公比为2的等比数列,所以2 n n a = . 3分 下同选. 18. 【解析解析】 (1)设BCx = ,在ABC 中,由余弦定理得 2 1 28422 () 2 xx =+ ,即 2 2240 xx += , 解
12、得4x = 或6x = (舍),所以4BC = 2 分 则 13 2 42 3 22 ABC S = = 3 分 因为 5 2 AB CD = ,所以 5 5 3 2 ABC ADC S S = 4 分 则梯形ABCD的面积+7 3 ABCADC SSS = 5 分 (2)设ABD = ,则BDC = , 2 BAC = , 2 3 DBC = , 6 BCA = 6 分 在ABC 中,由正弦定理得 2 sinsin 62 BC = 7 分 在BDC 中,由正弦定理得 5 2sin sin 3 BC = 8 分 两式相除得 2 2sin sin3 5sinsin 62 = ,展开得 31 2
13、(cossin) sin 22 cos31 5 (sincos) 22 + = 9 分 所以 22 5 3sin7sincos2 3cos0 = ,即 2 5 3tan7tan2 30 = 10 分 解得 2 3 tan 3 = 或 3 5 ,因为(,) 6 2 ,则 2 3 tan 3 = ,即 2 3 tan 3 ABD = .12 分 19.【解析解析】(1)取AC中点O,连结OM, 1 OC, 在ABC 中,因为M为AB中点,O为AC中点, 所以/OMBC,且 1 2 OMBC = ,1 分 又N为 11 BC中点, 11 /BCBC且 11 BCBC = , 所以 1 /C NBC,
14、且 1 1 2 C NBC = , 2 分 所以 1 /OMC N且 1 /OMC N,从而四边形 1 OMNC为平行四边形.3 分 所以 1 /MNOC, 4 分 又MN 平面 11 ACC A, 1 OC 平面 11 ACC A,所以/MN平面 11 ACC A. 5 分 (2)在直三棱柱 111 ABCABC 中, 1 BBAB , 1 3 2B M = , 1 4BB = , 所以 22 11 2BMB MBB = ,故2 2AB = , 222 ACBCAB += ,从而ACBC . 6 分 以C为原点,建立空间直角坐标系Cxyz 如图所示,则 ( )1,1,0M, ( ) 1 2,
15、0,4A, ( ) 1 0,2,4B, ( )0,1,4N, ( ) 1 1,1,4MB = ? ? , ( ) 1 1, 1,4MA = ? ? , ( )1,0,4MN = ? ? ,7 分 第 3 页 共 5 页 Q P F M A y xO 设平面 11 MAB的法向量为 ( ) 1 , ,x y z =n,则 11 11 0 0 MA MB = = ? ? ? ? n n ,即 40 40 xyz xyz += += ,解得 0 yx z = = , 令1x = ,得 ( ) 1 1,1,0 =n,8 分 设平面 1 MA N的法向量为 ( ) 2 , ,x y z =n,则 21
16、2 0 0 MA MN = = ? ? ? ? n n ,即 40 40 xyz xz += += ,解得 4 8 xz yz = = , 令1z = ,得 ( ) 2 4,8,1 =n,9 分 所以 12 12 12 122 2 cos, 329 = n n n n n n , 11 分 所以二面角 11 BAMN 的余弦值为2 2 3 .12 分 20.【解析解析】(1)0.58 ,y与x的相关关系为负相关, 2 分 且 0.75 ,故线性相关性不强,所以不建议继续做线性回归分析, 得到回归方程,拟合效果也会不理想.(相关指数 2 0.3364R )4 分 (2)建立22 列联表如下 人数
17、100 10515 AQI100 103545 合计204060 8 分 代入公式计算得 2 2 60 (35050) 10 15 45 2040 K = 10 分 查表知6.6351010.828 ,则 ( )fx 在区间( )0,2 至少有 12 24 , 11 xx aa = + 两个变号零点,故01a ,2 分 令 ( )0fx = ,得 2 1 m m x a = + , 2 1 n n x a = ,其中,m nZ,仅当1m = 时, ( ) 1 2 0,2 1 x a = + , 且在 1 x的左右两侧,导函数的值由正变负, 故01a 时, ( )fx在区间( )0,2 有唯一极
18、值点 0 2 1 x a = + ,此时 ( ) 000 sinsinfxaxax = 3 分 方法方法1将 0 2 1 x a = + 代入得 ( ) 0 22 sinsin 11 a fxa aa = + 22 sinsin 2 11 a a aa =+ + ( ) 2 1sin 1 a a a =+ + 4 分 当 21 12 a a + ,即 1 0 3 a 时,sinxx (*)知: ( ) ( ) 22 1sin12 11 aa aaa aa + + ,即当11 3 a 时,( )12aa , ( ) ( ) ( ) ( )122 1sin1sin1sin 111 aaa aaa
19、aaa +=+=+ + 由不等式(*)知:( ) ( ) ( ) ( ) ( ) 11 1sin11 11 aa aaa aa += + , 由知 ( ) ( ) 0 min 2, 1fxaa .6 分 方法方法2由 000 2 2 1 xaxx a = + , 0 2 1a x = ,代入得 ( ) ( ) 00000 0 2 sinsinsin 21 sinfxaxaxxx x = ,即 ( ) 00 0 2 sinfxx x = 以下用分析法可证: ( ) ( ) 0 min 2, 1fxaa 时,sinsinsin0faaa aaaa = , 第 5 页 共 5 页 所以 3 0 2
20、ff a ,7 分 由零点存在性定理知, ( )fx在区间 3 , 2a 至少有一个零点； 8 分 当11 2 a 时,2 a ,2a ,22a , ( ) ( )sin0,2sin20,fafa = = 9 分 由零点存在性定理知, ( )fx在区间( ),2 至少有一个零点；10 分 当 1 0 2 a , ( )0fx , ( )fx是增函数； 在区间( ),2 上, ( )0gx ,即 ( )g x递减,即 ( )fx 递减, ( ) ( )20fxf . 所以 ( )fx在区间( )0,2 没有零点,满足题意. 11 分 综上所述,若 ( )fx在区间( )0,2 没有零点,则正数a的取值范围是 1 0,2 . 12 分
