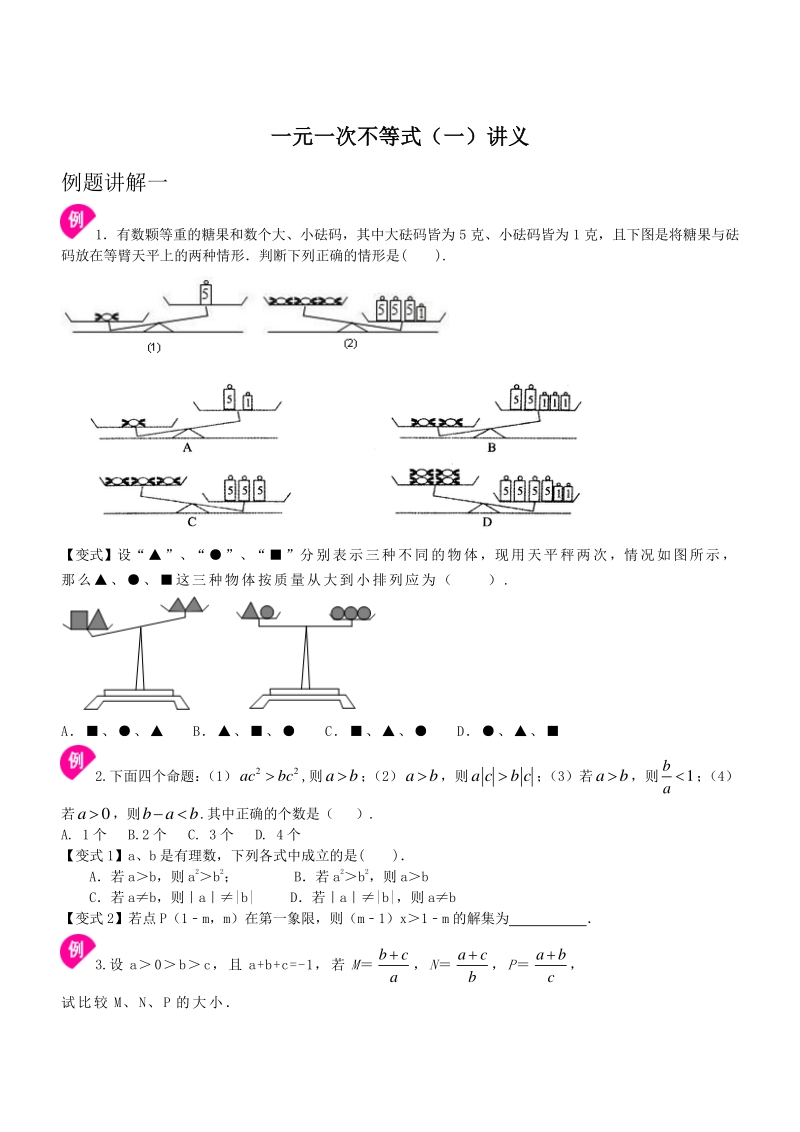
1、一元一次不等式一元一次不等式（一）（一）讲义讲义 例题讲解一 1有数颗等重的糖果和数个大、小砝码，其中大砝码皆为 5 克、小砝码皆为 1 克，且下图是将糖果与砝 码放在等臂天平上的两种情形判断下列正确的情形是( ). 【变式】设“”、“”、“”分别表示三种不同的物体，现用天平秤两次，情况如图所示， 那么、这三种物体按质量从大到小排列应为（ ）. A、 B、 C、 D、 2.下面四个命题： （1）,则； （2），则； （3）若，则； （4） 若，则.其中正确的个数是（ ）. A. 1 个 B.2 个 C. 3 个 D. 4 个 【变式 1】a、b 是有理数，下列各式中成立的是( ) A若 ab，
2、则 a 2b2； B若 a2b2，则 ab C若 ab，则a|b| D若a|b|，则 ab 【变式 2】若点 P（1m，m）在第一象限，则（m1）x1m 的解集为 3.设 a0bc，且 a+b+c=-1，若M，N，P， 试比较 M、N、P 的大小 22 acbcababa cb cab1 b a 0abab bc a ac b ab c 4.【提出问题】已知 xy=2，且 x1，y0，试确定 x+y 的取值范围 【分析问题】先根据已知条件用一个量如 y 取表示另一个量如 x，然后根据题中已知量 x 的取值范围，构建另 一量 y 的不等式，从而确定该量 y 的取值范围，同法再确定另一未知量 x
3、的取值范围，最后利用不等式性质即 可获解 例题讲解二 1下列式子哪些是一元一次不等式？哪些不是一元一次不等式？为什么？ （1） （2） （3） （4） （5） 2.求不等式的非负整数解，并把它的解在数轴上表示出来 【变式 1】解不等式： 【变式 2】代数式的值不大于的值，求 x 的范围 3.m 为何值时，关于 x 的方程：的解大于 1？ 0 x 1 x 1 2x 2 3yx1x 2x2) 1 4 x ( 3 2 2 3 6151 632 xmm x 【变式】已知关于方程的解是非负数，是正整数，则 4.若关于 x，y 的二元一次方程组的解满足 xy3.5，求出满足条件的 m 的所有正整 数解 5
4、.若关于的不等式只有三个正整数解，求的取值范围. 【变式】已知的解集中的最大整数为 3，则的取值范围是 6. 若关于的不等式的解集为，则关于的不等式的解 集 例题讲解三 1.（2016深圳）解不等式组： 【变式】解不等式组 无解则 a 的取值范围是 ( ) Aa1 Bal Ca1 Da1 x 3 x2 3 mx2 x mm xax a ax a xnmx 5 3 x x0n5mx)nm2( 3(2)4 2 3 xx ax x 2. 不等式组是否存在整数解？如果存在请求出它的解；如果不存在要说 【变式】解不等式组，并写出它的所有非负整数解 3.试确定实数 a 的取值范围使不等式组 恰好有两个整数
5、解 【变式】. .已知a是自然数，关于x的不等式组的解集是x2，求a的值 4.求不等式（2x1） （x+3）0 的解集 解：根据“同号两数相乘，积为正”可得：或 解得 x ；解得 x3 不等式的解集为 x 或 x3 请你仿照上述方法解决下列问题： （1）求不等式（2x3） （x+1）0 的解集 （2）求不等式0 的解集 3(2)5(4)2.(1) 56 2(2)1,.(2) 3 221 1.(3) 23 xx x x xx 1 0 23 544 (1) 33 xx a xxa 3x-4a, x-20 5.某校初三年级春游， 现有 36 座和 42 座两种客车供选择租用， 若只租用 36 座客车
6、若干辆， 则正好坐满； 若只租用 42 座客车，则能少租一辆，且有一辆车没有坐满，但超过 30 人；已知 36 座客车每辆租金 400 元，42 座客车每辆租金 440 元 (1)该校初三年级共有多少人参加春游? (2)请你帮该校设计一种最省钱的租车方案 【变式 1】 “向阳”中学某班计划用勤工俭学收入的 66 元，同时购买单价分别为 3 元、2 元、1 元的甲乙丙三种 纪念品，奖励参加校“艺术节”活动的同学已知购买的乙种纪念品比购买的甲种纪念品多 2 件，而购买的甲 种纪念品不少于 10 件，且购买甲种纪念品费用不超过总费用的一半，若购买的甲、乙、丙三种纪念品恰好用了 66 元钱，问可有几种
7、购买方案，每种方案中购买甲乙丙三种纪念品各多少件？ 【变式 2】5.12 四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作 拟派 30 名医护 人员，携带 20 件行李（药品、器械） ，租用甲、乙两种型号的汽车共 8 辆，日夜兼程赶赴灾区经了解，甲种 汽车每辆最多能载 4 人和 3 件行李，乙种汽车每辆最多能载 2 人和 8 件行李 (1) 设租用甲种汽车x辆，请你设计所有可能的租车方案； (2) 若甲、乙汽车的租车费用每辆分别为 8000 元、6000 元，请你选择最省钱的租车方案 同步练习一 一、选择题一、选择题 1已知关于 x 的不等式是一元一次不等式，那么 m 的值是
8、( ) . . Am1 Bm1 Cm-1 D不能确定 2由得到，则 a 应该满足的条件是（ ）. . Aa0 Ba0 Ca0 Da 为任意实数 3已知，如果，则 x 的取值范围是（ ）. . Ax2 Bx2 Cx-2 Dx-2 4设 a，b 是常数，不等式 + 0 的解集为 x ，则关于 x 的不等式 bx-a0 的解集是（ ） | | (1)0 m mx mn 22 mana 1 25yx 2 23yx 12 yy Ax Bx- Cx- Dx 5不等式1 的正整数解的个数是（ ） A1 个 B2 个 C3 个 D4 个 6.关于的不等式的解集如图所示，则的值是（ ）. A0 B2 C -2
9、D-4 二二、填空题填空题 7 （2016绍兴）不等式+2 的解是 8若不等式（3m-2）x7 的解集为 x，则 m 的值为 9比较大小：_. . 10已知-4 是不等式的解集中的一个值，则的范围为_. . 11若关于 x 的不等式只有六个正整数解，则 a 应满足_. . 12.已知的解集中的最小整数为，则的取值范围是 . . 三、解答题三、解答题 13若 m、n 为有理数，解关于 x 的不等式(m 21)xn 14.当 x 为何值时，代数式- x+3 的值比 6x-3 的值大 15.当时，求关于 x 的不等式的解集 16.已知 A2x 23x2，B2x24x5，试比较 A 与 B 的大小 同
10、步练习二 一、选择题一、选择题 1不等式组的解集是 x1，则 m 的取值范围是（ ） x2ax2a 22 336ab 22 241ab 5axa 30 xa ax 2a 3 10 )3(2 k k kx xk 4 )5( Am1 Bm1 Cm0 Dm0 2若不等式组有实数解则实数 m 的取值范围是 ( ) A B C D 3若关于 x 的不等式组无解，则 a 的取值范围是 ( ) Aa1 Bal C1 Da1 4关于 x 的不等式的整数解共有 4 个，则 m 的取值范围是 ( ) A6m7 B6m7 C6m7 D6m7 5某班有学生 48 人，每人都会下象棋或者围棋，且会下象棋的人数比会下围棋
11、的人数的 2 倍少 3 人，两种棋 都会下的至多 9 人，但不少于 5 人，则会下围棋的人有 （ ） A20 人 B19 人 C11 人或 13 人 D20 人或 19 人 6某城市的一种出租车起步价是 7 元（即在 3km 以内的都付 7 元车费） ，超过 3km 后，每增加 1km 加价 1.2 元 （不足 1km 按 1km 计算） ，现某人付了 14.2 元车费，求这人乘的最大路程是（ ） A10km B9 km C8km D7 km 二二、填空题填空题 7.已知，且，则 k 的取值范围是_ 8不等式组 x xm 1 有 3 个整数解，则 m 的取值范围是 9如果不等式组的解集是 0
12、x1，那么 a+b 的值为_ 10将一筐橘子分给几个儿童，若每人分 4 个，则剩下 9 个橘子；若每人分 6 个，则最后一个孩子分得的橘子 将少于 3 个，则共有_个儿童，_个橘子 11对于整数 a、b、c、d，规定符号已知，则 b+d 的值是_ 12. 在ABC 中，三边为、, （1）如果，那么的取值范围是 ； （2）已知ABC 的周长是 12，若是最大边，则的取值范围是 ； （3） 三、解答题三、解答题 530 0 x xm 5 3 m 5 3 m 5 3 m 5 3 m 3(2)4 32 xx xax 0 721 xm x 24 221 xyk xyk 10 xy 2 2 23 x a
13、xb ab acbd dc a b c 3ax4bx28c x bb cabbacacbcba 13.解下列不等式组 (1) (2) （3） （4） 14.已知：关于 x，y 的方程组的解是正数，且 x 的值小于 y 的值 （1）求的范围； （2）化简|8+11|-|10+1| 15.某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球 （每个气排球的价格都相同， 每个篮球的 价格都相同） 经洽谈，购买 1 个气排球和 2 个篮球共需 210 元；购买 2 个气排球和 3 个篮球共需 340 元 （1）每个气排球和每个篮球的价格各是多少元？ （2）该体育馆决定从这家体育用品商店一次性购买
14、气排球和篮球共 50 个，总费用不超过 3200 元，且购买气排 球的个数少于 30 个，应选择哪种购买方案可使总费用最低？最低费用是多少元？ 2 31 3 1 3(1)6 x x xx 2 1 21x 210 310 320 x x x 21 5 3 x 27 243 xya xya a aa 一元一次不等式一元一次不等式（一）参考答案（一）参考答案 例题讲解一 1有数颗等重的糖果和数个大、小砝码，其中大砝码皆为 5 克、小砝码皆为 1 克，且下图是将糖果与砝 码放在等臂天平上的两种情形判断下列正确的情形是( ). 【思路点拨】根据图示可知 1 个糖果的质量5 克，3 个糖果的质量16 克，
15、依此求出 1 个糖果的质量取值范 围，再在 4 个选项中找出情形正确的 【答案】D. 【解析】 解：由图(1)知，每一个糖果的重量大于 5 克，由图(2)知：3 个糖果的重量小于 16 克，即每一个糖果的重量小 于克故 A 选项错；两个糖果的重量小于克故 B 选项错；三个糖果的重量大于 15 克小于 16 克故 C 选项错，四个糖果的重量小于克故 D 选项对 【总结升华】观察图示，确定大小本题涉及的知识点是不等式，涉及的数学思想是数形结合思想，解决问题 的基本思路是根据图示信息列出不等式 举一反三：举一反三： 【变式】设“”、“”、“”分别表示三种不同的物体，现用天平秤两次，情况如图所示， 那
16、么、这三种物体按质量从大到小排列应为（ ）. A、 B、 C、 D、 【答案】C. 类型二、类型二、不等式的基本性质不等式的基本性质 16 3 322 10 33 16641 421 333 2.下面四个命题： （1）,则； （2），则； （3）若，则； （4） 若，则.其中正确的个数是（ ）. A. 1 个 B.2 个 C. 3 个 D. 4 个 【答案】B. 【解析】(1)由得，因为0,所以，正确； （2）因为，当时，所以错误； （3）因为，当时，没有意义，而当时，所以错误； （4）因为，所以，正确. 【总结升华】不等式的基本性质是不等式变形的主要依据，要认真弄清楚不等式的基本性质与等式的
17、基本性质 的异同点，特别是不等式两边同时乘以（或除以）同一个数时，不仅要考虑这个数不等于 0，而且先必须确定 这个数是正数还是负数. 举一反三：举一反三： 【变式 1】a、b 是有理数，下列各式中成立的是( ) A若 ab，则 a 2b2； B若 a2b2，则 ab C若 ab，则a|b| D若a|b|，则 ab 【答案】D. 【变式 2】若点 P（1m，m）在第一象限，则（m1）x1m 的解集为 【答案】x1. 解：点 P（1m，m）在第一象限， 1m0， 即 m10； 不等式（m1）x1m， （m1）x（m1） ， 不等式两边同时除以 m1，得： x1， 故答案为：x1 3.设 a0bc，
18、且 a+b+c=-1，若M，N，P， 试比较 M、N、P 的大小 【答案与解析】a+b+c=-1， b+c=-1-a， M=1， 同理可得 N=1，P=1； 又a0bc， 0， 22 acbcababa cb cab1 b a 0abab 22 acbc0c 2 cab ab0c a cb c ab0a b a 0a1 b a 0a0a bab bc a ac b ab c 1 a a 1 a 1 b 1 c 1 a 1 c 1 b 1111 即 MPN 【总结升华】本题考查不等式的基本性质，关键是 M、N、P 的等价变形，利用了整体思想消元， 转化为 a、b、c 的大小关系 4.（2016
19、春唐河县期中） 【提出问题】已知 xy=2，且 x1，y0，试确定 x+y 的取值范围 【分析问题】先根据已知条件用一个量如 y 取表示另一个量如 x，然后根据题中已知量 x 的取值范围，构建另 一量 y 的不等式，从而确定该量 y 的取值范围，同法再确定另一未知量 x 的取值范围，最后利用不等式性质即 可获解 【解决问题】解：xy=2，x=y+2 又x1，y+21，y1 又y0，1y0， 同理得 1x2 由+得1+1y+x0+2 x+y 的取值范围是 0 x+y2 【尝试应用】已知 xy=3，且 x1，y1，求 x+y 的取值范围 【思路点拨】先根据已知条件用一个量如 y 取表示另一个量如
20、x，然后根据题中已知量 x 的取值范围，构建另 一量 y 的不等式，从而确定该量 y 的取值范围，同法再确定另一未知量 x 的取值范围，最后利用不等式性质即 可获解 【答案与解析】 解：xy=3， x=y3 又x1， y31， y2 又y1， 1y2， 同理得2x1 由+得 12y+x21 x+y 的取值范围是1x+y1 【总结升华】 此题主要考查了等量代换及不等式的基本性质 （1） 不等式的两边同时乘以 （或除以） 同一个正数， 1 a 1 c 1 b 不等号的方向不变； （2）不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变； （3）不等式的两 边同时加上（或减去）同一个数或同一
21、个含有字母的式子，不等号的方向不变 例题讲解二 1下列式子哪些是一元一次不等式？哪些不是一元一次不等式？为什么？ （1） （2） （3） （4） （5） 【思路点拨】根据一元一次不等式的定义判断 【答案与解析】 解：(1)是一元一次不等式 （2） （3）(4)(5)不是一元一次不等式，因为： （2）中分母中含有字母， （3）未知数 的最高次数不是 1 次， （4）不等式左边含有两个未知数， （5）不是不等式，是一元一次方程 【总结升华】一元一次不等式的定义主要由三部分组成：不等式的左右两边分母不含未知数；不等式中只 含一个未知数；未知数的最高次数是 1，三个条件缺一不可 类型二、解一元一次不等
22、式类型二、解一元一次不等式 2.求不等式的非负整数解，并把它的解在数轴上表示出来 【思路点拨】首先应对不等式的左右代数式化简，使得分子、分母上的小数化成整数，然后根据不等式的性质 2 去掉分母等进行求解不等式，再在解集中求出符合条件的非负整数 【答案与解析】 解：原不等式可化为：去分母， 得 6（4x10）15（5x）10（32x） 去括号，得 24x6075+15x3020 x 移项，得 24x+15x+20 x30+60+75 合并同类项，得 59x165 把系数化为 1，得 x， 解集 x的非负整数解是：0，1，2， 数轴表示是： 【总结升华】 本题主要考查了不等式的解法， 求出解集是解
23、答本题的关键， 解不等式应根据不等式的基本性质 举一反三：举一反三： 【变式 1】解不等式： 0 x 1 x 1 2x 2 3yx1x 2x2) 1 4 x ( 3 2 2 3 【答案】 解：去括号，得 移项、合并同类项得： 系数化 1，得 故原不等式的解集是. 【变式 2】代数式的值不大于的值，求 x 的范围 【答案】 解：根据题意得：解不等式， 去分母得：63（3x1）2（12x） ， 去括号得：69x+324x， 移项得：4x9x263， 合并同类项得：5x7， 解得：x 3.m 为何值时，关于 x 的方程：的解大于 1？ 【思路点拨】从概念出发，解出方程（用 m 表示 x） ，然后解不
24、等式 【答案与解析】 解： x-12m+2=6x-15m+3 5x=3m-1 由 解得 m2 【总结升华】此题亦可用 x 表示 m，然后根据 x 的范围运用不等式基本性质推导出 m 的范围 举一反三：举一反三： 【变式】已知关于方程的解是非负数，是正整数，则 【答案】1 或 2. 4.（2016杭州模拟）若关于 x，y 的二元一次方程组的解满足 xy3.5，求出满足条 件的 m 的所有正整数解 【思路点拨】先解出方程组再解不等式 【答案与解析】 2x31 4 x 6x 4 3 8x 8x 6151 632 xmm x 31 5 m x 31 1 5 m x 3 x2 3 mx2 x mm 解：
25、由方程组的两个方程相减得：xy=0.5m2 0.5m23.5， m3， 满足条件的 m 的所有正整数解为 m=1，m=2 【总结升华】本题考查了巧解二元一次方程组，有时根据具体问题，可以不必解出的具体值能得出关于 m 的不等式是解此题的关键 类型二、类型二、不等式的解及解集不等式的解及解集 5.若关于的不等式只有三个正整数解，求的取值范围. 【思路点拨】首先根据题意确定三个正整数解，然后再确定 a 的范围 【答案】. 【解析】 解：不等式只有三个正整数解， 三个正整数解为：1，2，3， ， 【总结升华】此题主要考查了一元一次不等式的整数解，做此题的关键是确定好三个正整数解 举一反三：举一反三：
26、 【变式】已知的解集中的最大整数为 3，则的取值范围是 【答案】. 类型四、逆用不等式的解集类型四、逆用不等式的解集 6. 若关于的不等式的解集为，则关于的不等式的解 集 【思路点拨】先根据第一个不等式确定的关系或符号，再代入第二个不等式进行求解 【答案】. 【解析】 解：由的解集为可知得：，即 将上式代入， 化简整理得：，又 所以. 【总结升华】解答本题的关键是根据不等号的方向改变确定 y,x xax a 4a3 ax 4a3 ax a 4a3 xnmx 5 3 x x0n5mx)nm2( n,m 7 10 x nmx 5 3 x 0m 5 3 m n m 5 3 n 0n5mx)nm2(
27、m2mx 5 7 0m 7 10 x 0m 例题讲解三 1.（2016深圳）解不等式组： 【思路点拨】按照解不等式组的基本步骤进行求解就可以了 【答案与解析】 解：， 解得 x2， 解得 x1， 则不等式组的解集是1x2 【总结升华】求出不等式、的解集后，应取其公共部分作为不等式组的解集，解集的规律：同大取大；同 小取小；大小小大中间找；大大小小找不到 举一反三：举一反三： 【变式】解不等式组 无解则 a 的取值范围是 ( ) Aa1 Bal Ca1 Da1 【答案】B 2. 不等式组是否存在整数解？如果存在请求出它的解；如果不存在要说 明理由. 【思路点拨】 解这类问题的第一步是分别求出各个
28、不等式的解集； 第二步借助数轴以确定不等式组的公共解集； 最后看公共解集中是否存在整数解. 【答案与解析】 解：解不等式（1） ，得：x2； 3(2)4 2 3 xx ax x 3(2)5(4)2.(1) 56 2(2)1,.(2) 3 221 1.(3) 23 xx x x xx 解不等式（2） ，得：x-3； 解不等式（3） ，得：x-2； 在数轴上分别表示不等式（1） 、 （2） 、 （3）的解集： 原不等式组的解集为：-2x2. 原不等式组的整数解为：-2、-1、0、1. 【总结升华】 求不等式组的解集就是求不等式组中所有不等式解集的公共部分.对于三个以上的不等式有时不容 易得到公共解
29、集，于是常常借助数轴的直观性，这样较容易确定其解集.在数轴上表示点的位置，要注意空心圈 与实心圆点的不同用法. 举一反三：举一反三： 【变式】 （2015北京）解不等式组，并写出它的所有非负整数解 【答案】解：， 由得：x2； 由得：x ， 不等式组的解集为2x ， 则不等式组的所有非负整数解为：0，1，2，3 3.试确定实数 a 的取值范围使不等式组 恰好有两个整数解 【思路点拨】先确定其解集，再判断出整数解，最后利用数轴确定 a 的范围 【答案与解析】 解：由不等式，去分母得 3x+2(x+1)0， 去括号，合并同类项，系数化为 1 后得 x 由不等式去分母得 3x+5a+44x+4+3a
30、，可解得 x2a 所以原不等式组的解集为， 因为该不等式组恰有两个整数解： 0 和 l， 故有： 12a2， 所以： 【总结升华】 此题考查的是一元一次不等式组的解法， 得出 x 的整数解， 再根据 x 的取值范围求出 a 的值即可 1 0 23 544 (1) 33 xx a xxa 1 0 23 xx 2 5 544 (1) 33 a xxa 2 2 5 xa 1 2 a 【高清课堂：高清课堂：第二讲第二讲 一元一次不等式组的解法一元一次不等式组的解法 370096370096 例例 6 6】 举一反三：举一反三： 【变式】. .已知a是自然数，关于x的不等式组的解集是x2，求a的值 【答
31、案】解：解第一个不等式，得解集， 解第二个不等式，得解集， 不等式组的解集为x2， ，即，又为自然数， 或 1 或 2 类型二、类型二、解特殊的一元一次不等式组解特殊的一元一次不等式组 4.（2015黔西南州）求不等式（2x1） （x+3）0 的解集 解：根据“同号两数相乘，积为正”可得：或 解得 x ；解得 x3 不等式的解集为 x 或 x3 请你仿照上述方法解决下列问题： （1）求不等式（2x3） （x+1）0 的解集 （2）求不等式0 的解集 【答案与解析】 解： （1）根据“异号两数相乘，积为负”可得或， 解得不等式组无解；解得，1x ； （2）根据“同号两数相乘，积为正”可得， 解得
32、，x3，解得，x2， 故不等式组的解集为：x3 或 x2 【总结升华】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找 不到”的原则是解答此题的关键 类型三、类型三、一元一次不等式组的应用一元一次不等式组的应用 5.某校初三年级春游， 现有 36 座和 42 座两种客车供选择租用， 若只租用 36 座客车若干辆， 则正好坐满； 3x-4a, x-20 4 3 a x 2x 4 2 3 a 2aa 0a 若只租用 42 座客车，则能少租一辆，且有一辆车没有坐满，但超过 30 人；已知 36 座客车每辆租金 400 元，42 座客车每辆租金 440 元 (1)该
33、校初三年级共有多少人参加春游? (2)请你帮该校设计一种最省钱的租车方案 【思路点拨】 本题的关键语句是：“若只租用 42 座客车， 则能少租一辆， 且有一辆车没有坐满， 但超过 30 人” 理 解这句话，有两层不等关系 (1)租用 36 座客车 x 辆的座位数小于租用 42 座客车(x-1)辆的座位数 (2)租用 36 座客车 x 辆的座位数大于租用 42 座客车(x-2)辆的座位数+30 【答案与解析】 解：(1)设租 36 座的车 x 辆 据题意得：， 解得： 由题意 x 应取 8，则春游人数为：368288(人) (2)方案：租 36 座车 8 辆的费用：84003200(元)， 方案
34、：租 42 座车 7 辆的费用：74403080(元)， 方案：因为 426+361288，所以租 42 座车 6 辆和 36 座车 1 辆的总费用： 644014003040(元) 所以方案：租 42 座车 6 辆和 36 座车 1 辆最省钱 【总结升华】本例不等关系相对隐蔽，需要在审题过程中加以挖掘 举一反三：举一反三： 【变式 1】 “向阳”中学某班计划用勤工俭学收入的 66 元，同时购买单价分别为 3 元、2 元、1 元的甲乙丙三种 纪念品，奖励参加校“艺术节”活动的同学已知购买的乙种纪念品比购买的甲种纪念品多 2 件，而购买的甲 种纪念品不少于 10 件，且购买甲种纪念品费用不超过总
35、费用的一半，若购买的甲、乙、丙三种纪念品恰好用了 66 元钱，问可有几种购买方案，每种方案中购买甲乙丙三种纪念品各多少件？ 【答案】 解：设购买的甲、乙、丙三种纪念品件数分别为 x、y、z，由题意得： 且 由方程组得： 解不等式组得：10 x11 x 为整数，x10 或 x11 当 x10 时，y12，z12 当 x11 时，y13，z7 可有两种方案购买 【高清课堂：高清课堂：实际问题与一元一次不等式组实际问题与一元一次不等式组 409416409416 练习练习】 3642(1) 3642(2)30 xx xx 7 9 x x 2 6623 xy zyx 2 66 3 10 x x xz
36、xy 562 2 【变式 2】5.12 四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作 拟派 30 名医护 人员，携带 20 件行李（药品、器械） ，租用甲、乙两种型号的汽车共 8 辆，日夜兼程赶赴灾区经了解，甲种 汽车每辆最多能载 4 人和 3 件行李，乙种汽车每辆最多能载 2 人和 8 件行李 (1) 设租用甲种汽车x辆，请你设计所有可能的租车方案； (2) 若甲、乙汽车的租车费用每辆分别为 8000 元、6000 元，请你选择最省钱的租车方案 【答案】 解：（1）设租用甲种汽车x辆，则租用乙种汽车，则： ， 解得：， 应为整数，或 8， 有两种租车方案，分别为： 方案
37、 1：租甲种汽车 7 辆，乙种汽车 1 辆；方案 2：租甲种汽车 8 辆，乙种汽车 0 辆 （2）租车费用分别为： 方案 1: 800076000162000（元） ；方案 2：8000:864000（元） 方案 1 花费最低，所以选择方案 1 同步练习一 一、选择题一、选择题 1已知关于 x 的不等式是一元一次不等式，那么 m 的值是( ) . . Am1 Bm1 Cm-1 D不能确定 2由得到，则 a 应该满足的条件是（ ）. . Aa0 Ba0 Ca0 Da 为任意实数 3已知，如果，则 x 的取值范围是（ ）. . Ax2 Bx2 Cx-2 Dx-2 4设 a，b 是常数，不等式 +
38、0 的解集为 x ，则关于 x 的不等式 bx-a0 的解集是（ ） Ax Bx- Cx- Dx 5 （2016南充）不等式1 的正整数解的个数是（ ） (8)x 42(8)30 38(8)20 xx xx 4 78 5 x x7x | | (1)0 m mx mn 22 mana 1 25yx 2 23yx 12 yy A1 个 B2 个 C3 个 D4 个 6.关于的不等式的解集如图所示，则的值是（ ）. A0 B2 C -2 D-4 二二、填空题填空题 7 （2016绍兴）不等式+2 的解是 8若不等式（3m-2）x7 的解集为 x，则 m 的值为 9比较大小：_. . 10已知-4 是
39、不等式的解集中的一个值，则的范围为_. . 11若关于 x 的不等式只有六个正整数解，则 a 应满足_. . 12.已知的解集中的最小整数为，则的取值范围是 . . 三、解答题三、解答题 13若 m、n 为有理数，解关于 x 的不等式(m 21)xn 14.当 x 为何值时，代数式- x+3 的值比 6x-3 的值大 15.当时，求关于 x 的不等式的解集 16.已知 A2x 23x2，B2x24x5，试比较 A 与 B 的大小 【答案与解析】【答案与解析】 一、选择题一、选择题 1. 【答案】C； 【解析】，所以； 2. 【答案】C； 【解析】由得到，不等式两边同乘以，不等号方向没变，所以；
40、 3. 【答案】B； 【解析】，即，解得：. 4. 【答案】B； x2ax2a 22 336ab 22 241ab 5axa 30 xa ax 2a 3 10 )3(2 k k kx xk 4 )5( 1,10mm 1m mn 22 mana 2 a 2 0,0aa即 12 yy2523xx 2x 【解析】解：解不等式 + 0， 移项得： - ， 解集为 x ， - = ，且 a0 b=-5a0， =- 解不等式 bx-a0， 移项得：bxa， 两边同时除以 b 得：x ， 即 x- 故选 B 5.【答案】D 【解析】解：去分母得：3（x+1）2（2x+2）6， 去括号得：3x+34x+46，
41、 移项得：3x4x463， 合并同类项得：x5， 系数化为 1 得：x5， 故不等式的正整数解有 1、2、3、4 这 4 个. 6. 【答案】A； 【解析】 因为不等式的解集为， 再观察数轴上表示的解集为， 因此， 解得 二、填空题二、填空题 【解析】去分母，得：3（3x+13）4x+24， 去括号，得：9x+394x+24， 移项，得：9x4x2439， 合并同类项，得：5x15， 系数化为 1，得：x3， 故答案为：x3 8. 【答案】-； 2ax2 2 2a x 1x1 2 2a 0a 【解析】解：（3m-2）x7 的解集为 x， x， =- ，解得 m=- 故答案为：- 9. 【答案】
42、； 【解析】， 所以. 10 【答案】； 【解析】将-4 代入得：，所以. 11.【答案】； 【解析】由已知得：，即. 12.【答案】 【解析】画出数轴分析得出正确答案. 三、解答题三、解答题 13.【解析】 解： (m 21)xn ， 两边同除以负数（m 21）得： . 原不等式的解集为：. 14.【解析】 解：由题意得，- x+36x-3， 去分母得，-x+186（6x-3） ， 去括号得，-x+1836x-18， 移项得，-x-36x-18-18， 合并同类项，-37x-36， 把 x 的系数化为 1 得，x 因此，当 时，代数式- x+3 的值比 6x-3 的值大 15.【解析】 22
43、2222 (336)(241)50ababab 2222 336241abab 5 4 a 45a 5 4 a 1821a 3 a x 67 3 a 1821a 2a3 22 10,10.mm 22 11 nn x mm 2 1 n x m 解： 16.【解析】 解：, 当时，；当时，；当时，. 同步练习二 一、选择题一、选择题 1 （2016聊城）不等式组的解集是 x1，则 m 的取值范围是（ ） Am1 Bm1 Cm0 Dm0 2若不等式组有实数解则实数 m 的取值范围是 ( ) A B C D 3若关于 x 的不等式组无解，则 a 的取值范围是 ( ) Aa1 Bal C1 Da1 4关
44、于 x 的不等式的整数解共有 4 个，则 m 的取值范围是 ( ) A6m7 B6m7 C6m7 D6m7 3 10 )3(2 k k 6 -18 10-kk 4k kx xk 4 )5( -54 -4kx kx k (4) kkx 4 k x k 7x7BA 1xBA 1xBA 1xBA 530 0 x xm 5 3 m 5 3 m 5 3 m 5 3 m 3(2)4 32 xx xax 0 721 xm x 5某班有学生 48 人，每人都会下象棋或者围棋，且会下象棋的人数比会下围棋的人数的 2 倍少 3 人，两种棋 都会下的至多 9 人，但不少于 5 人，则会下围棋的人有 （ ） A20
45、人 B19 人 C11 人或 13 人 D20 人或 19 人 6某城市的一种出租车起步价是 7 元（即在 3km 以内的都付 7 元车费） ，超过 3km 后，每增加 1km 加价 1.2 元 （不足 1km 按 1km 计算） ，现某人付了 14.2 元车费，求这人乘的最大路程是（ ） A10km B9 km C8km D7 km 二二、填空题填空题 7.已知，且，则 k 的取值范围是_ 8 （2016龙东地区）不等式组 x xm 1 有 3 个整数解，则 m 的取值范围是 9如果不等式组的解集是 0 x1，那么 a+b 的值为_ 10将一筐橘子分给几个儿童，若每人分 4 个，则剩下 9 个橘子；若每人分 6 个，则最后一个孩子分得的橘子 将少于 3 个，则共有_个儿童，_个橘子 11对于整数 a、b、c、d，规定符号已知，则 b+d 的值是_ 12. 在ABC 中，三边为、, （1）如果，那么的取值范围是 ； （2）已知ABC 的周长是 12，若是最大边，则的取值范围是 ； （3） 三、解答题三、解答题 13.解下列不等式组 (1)
