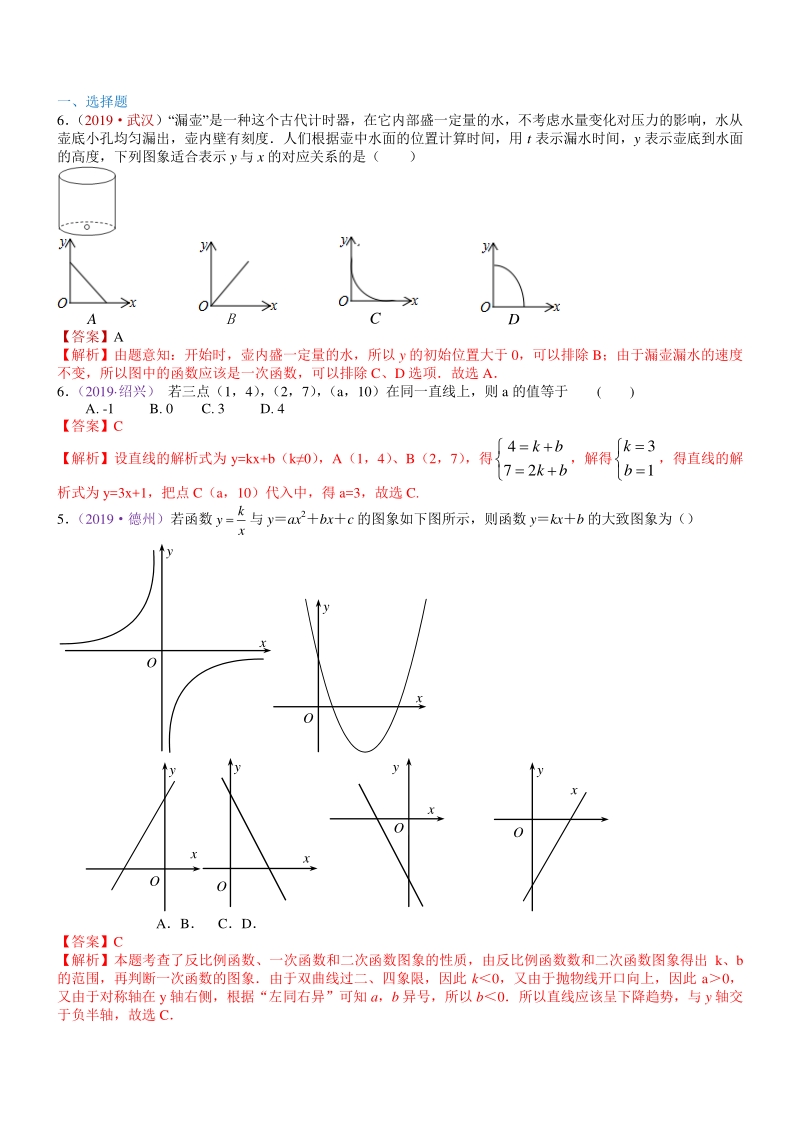
1、 一、选择题 6 （2019武汉）“漏壶”是一种这个古代计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从 壶底小孔均匀漏出，壶内壁有刻度人们根据壶中水面的位置计算时间，用 t 表示漏水时间，y 表示壶底到水面 的高度，下列图象适合表示 y 与 x 的对应关系的是（ ） 【答案】A 【解析】由题意知：开始时，壶内盛一定量的水，所以 y 的初始位置大于 0，可以排除 B；由于漏壶漏水的速度 不变，所以图中的函数应该是一次函数，可以排除 C、D 选项故选 A 6 （2019 绍兴） 若三点（1，4） ， （2，7） ， （a，10）在同一直线上，则 a 的值等于 ( ) A. -1 B
2、. 0 C. 3 D. 4 【答案】C 【解析】设直线的解析式为 y=kx+b（k0） ，A（1，4） 、B（2，7） ，得 4 72 kb kb ，解得 3 1 k b ，得直线的解 析式为 y=3x+1，把点 C（a，10）代入中，得 a=3，故选 C. 5 （2019德州）若函数 k y x 与 yax2bxc 的图象如下图所示，则函数 ykxb 的大致图象为（） AB CD 【答案】C 【解析】本题考查了反比例函数、一次函数和二次函数图象的性质，由反比例函数数和二次函数图象得出 k、b 的范围，再判断一次函数的图象由于双曲线过二、四象限，因此 k0，又由于抛物线开口向上，因此 a0，
3、又由于对称轴在 y 轴右侧，根据“左同右异”可知 a，b 异号，所以 b0所以直线应该呈下降趋势，与 y 轴交 于负半轴，故选 C O y O y x O y x O y x O y x O y x DCBA x 11（2019 德州） 在下列函数图象上任取不同两点 P1（x1， y1） 、 P2（x2， y2） ， 一定能使0 成立的是 （ ） Ay3x1（x0） Byx2+2x1（x0） Cy（x0） Dyx24x1（x0） 【答案】D 【解析】Ak30，y 随 x 的增大而增大，即当 x1x2时，必有 y1y2，当 x0 时，0，故 A 选项不符合； B 对称轴为直线 x1， 当 0 x
4、1 时 y 随 x 的增大而增大， 当 x1 时 y 随 x 的增大而减小， 当 0 x1 时：当 x1x2时，必有 y1y2，此时0，故 B 选项不符合；C当 x0 时，y 随 x 的增大 而增大，即当 x1x2时，必有 y1y2，此时0，故 C 选项不符合；D对称轴为直线 x2，当 x0 时 y 随 x 的增大而减小，即当 x1x2时，必有 y1y2，此时0，故 D 选项符合；故选 D 7 （2019苏州）若一次函数 y =kx+b（k、b 为常数，且 k0）的图象过点 A（0，-l） ，B(1，1)则不等式 kx+b1 的解集为 （ ） Ax0 Cx1 【答案】D 【解析】本题考查了一次
5、函数及其应用，如图所示：不等式 kx+b1 的解为 x1故选 D 第 7 题答图 8 （2019杭州）已知一次函数 y1=ax+b 和 y2=bx+a（ab） ，函数 y1和 y2的图象可能是（ ） A B C D 【答案】A 【解析】当0,0ab， 1 y、 2 y的图象都经过一、二、三象限；当0,0ab， 1 y、 2 y的图象都经过二、 三、 四象限； 当0,0ab， 1 y的图象都经过一、 三、 四象限， 2 y的图象都经过一、 二、 四象限； 当0,0ab， 1 y的图象都经过一、二、四象限， 2 y的图象都经过一、三、四象限.满足题意的只有 A. 11 （2019威海） x y 1
6、 O x y 1 O x y 1 O x y 1 O 甲、乙施工队分別从两端修一段长度为 380 米的公路.在施工过程中，乙队曾因技术改进而停工一天，之后加快 了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的. 施工时间/天 1 2 3 4 5 6 7 8 9 累计完成施工量/米 35 70 105 140 160 215 270 325 380 下列说法错误的是 A甲队每天修路 20 米 B乙队第一天修路 15 米 C乙队技术改进后每天修路 35 米 D前七天甲、乙两队修路长度相等 【答案】D 【解析】从表格当中观察自变量与函数的变化关系，从第 1 天到第 4 天可
7、以看出每天的变化规律相同，从第 5 天发生了改变，这说明正是乙队停工的那一天，从而推出甲队每天修路 20 米，故 A 正确；根据两队的合作从而 算得乙队第一天修路 15 米， 故 B 正确； 通过第 6 天累计完成的施工量， 能算出乙队技术改进后每天修路 35 米， 故 C 正确；因甲队每天修路 20 米，故前 7 天甲队一共修了 140 米，第 7 天两队累计完成施工量为 270 米，从而 算出乙队前 7 天一共修了 130 米，所以前 7 天甲乙两队修路长度不等，故 D 错误 8 （2019青岛）已知反比例函数 y= ab x 的图象如图所示，则二次函数 y=ax2-2x 和一次函数 y=
8、bxa 在同一平面 直角坐标系中的图象可能是 AB C D 【答案】C 【解析】观察反比例函数可知 a，b 同号，若 a，b 同为正，则- 2 2a 0,所以二次函数 y=ax2-2x 开口向上，与 x 轴 交于原点,对称轴在 x 轴正半轴,一次函数经过第一、 二、 三象限； 若 a， b 同为负， 则- 2 2a 0,所以二次函数 y=ax2-2x 开口向上，与 x 轴交于原点,开口向下，对称轴在 x 轴负半轴,一次函数经过第二、三、四象限,根据以上规则判 定只有 C 正确,故选 C. 5 （2019 江西） 已知正比例函数 1 y的图象与反比例函数 2 y的图象相交于点 A(2， 4)，
9、下列说法正确的是 （ ） A.反比例函数 2 y的解析式是 x y 8 2 B.两个函数图象的另一交点坐标为(2，-4) C.当 x-2 或 0 x2 时， 1 y 2 y D.正比例函数 1 y与反比例函数 2 y都随 x 的增大而增大 【答案】C 【解析】设正比例函数解析式为 1 y=ax，反比例函数解析式为 x b y 2 ， 正比例函数 1 y的图象与反比例函数 2 y的图象相交于点 A(2，4)， 2a=4， 2 4 b ，a=2，b=8，正比例函数解析式为 1 y=2x，反比例函数解析式为 x y 8 2 .故 A 错误； 由 x y xy 8 2 得 4 2 y x 或 4 2
10、y x ，两个函数图象的另一交点坐标为(-2，-4) ，故 B 错误； 由函数图象可知：当 x-2 时， 1 y 2 y ；当 0 x2 时， 1 y 2 y .C 正确. 正比例函数 1 y随 x 的增大而增大；在每个象限内，反比例函数 2 y都随 x 的增大而减小.D 错误. 5 （2019益阳）下列函数中，y 总随 x 的增大面减小的是（ ） A.y=4x B.y=-4x C.y=x-4 D. 2 xy 【答案】B 【解析】y 总随 x 的增大面减小，y=-4x.故选 B. 10（2019 娄底） 如图 （4） ， 直线y xb 和2ykx与 x 轴分别交于点 A （2， 0） ， 点
11、B （3， 0） ， 则 0 20 xb kx 的解集为（ ） A. x3 C x3 D 2x2；在 x 轴 上 3 的左边，对应于每一 个 x 的值，函数值2ykx都落在 x 轴的上方，即不等式 kx+20 的解集为 x3；再根据“大小小大取中间” 即可得出不等式组 0 20 xb kx 的解集 观察函数图象得到 不等式0 xb的解集为 x2， 不等式 kx+20 的解集为 x3； 所以不等式组 0 20 xb kx 的解集为2x3 故选 A 8 （2019黄冈） 已知林茂的家、体育场、文具店在同一直线上，图中的信息反映的过程是林凌从家跑步去体 育场，在体育场锻炼了一阵后又走到文具店买笔，然
12、后再走回家、图中x表示时间，y表示林茂离家的距离.依据 图中的信息，下列说法错误的是（ ） A.体育场离林茂家2.5km B.体育场离文具店1km C.林茂从体育场出发到文具店的平均速度是50m/min D.林茂从文具店回家的平均速度是60m/min 【答案】C 【解析】选项A，林茂从家到体育场离林茂家2.5km，正确； 选项B，林茂从体育场到文具店的距离是2.5-1.51km，正确； 选项C，林茂从体育场出发到文具店的平均速度是 25001200200 45303 m/min，错误； 选项D，林茂从文具店回家的平均速度是 1500 9065 60m/min，正确. 10 （2019陇南）如图
13、，在矩形 ABCD 中，ABAD，对角线 AC，BD 相交于点 O，动点 P 由点 A 出发，沿 ABBCCD 向点 D 运动设点 P 的运动路程为 x， AOP 的面积为 y， y 与 x 的函数关系图象如图所示， 则 AD 边的长为（ ） A3 B4 C5 D6 【答案】B 【解析】由图可得，AB+BC=7，设 BC=x，则 AB=7-x，AOB 的面积是 3，点 O 为 AC 的中点， (7) 2 2 x x =3，解得，x=3 或 x=4，ABBC，BC=4，AD=4，故选 B 1. (2019聊城)某快递公司每天上午 9：0010：00 为集中揽件和派件时段,甲仓库用来揽收快件,乙仓
14、库用来 派发快件,该时段内甲,乙两仓库的快件数量 y(件)与时间 x(分)之间的函数图象如图所示,那么当两仓库快递件 数相同时,此刻的时间为（ ） A.9：15 B.9：20 C.9：25 D.9：30 E DC B A y/km x/min1530456590 1.5 2.5 0 【答案】B 【解析】由图可知,两仓库的快件数量 y(件)与时间 x(分)都是一次函数关系,故用待定系数法求出 y甲6x+40,y乙 4x+240,令 y甲y乙,得 x20,则两仓库快递件数相同时的时间为 9：20. 2. (2019 聊城)如图,在 RtABO 中,OBA90,A(4,4),点 C 在边 AB 上,
15、且 AC CB 1 3 ,点 D 为 OB 的中点,点 P 为 边 OA 上的动点,当点 P 在 OA 上移动时,使四边形 PDBC 周长最小的点 P 的坐标为 A.(2,2) B.( 5 2 , 5 2 ) C.( 8 3 , 8 3 ) D.(3,3) 【答案】C 【解析】由题可知：A(4,4),D(2,0),C(4,3),点 D 关于 AO 的对称点 D(0,2),设 lDC：ykx+b,将 D(0,2),C(4,3)代入,可 得 y 1 4 x+2,与 yx 联立,得,x 8 3 ,y 8 3 ,P( 8 3 , 8 3 )故选 C. 3. （2019潍坊）如图，在矩形 ABCD 中，
16、AB=2，BC=3，动点 P 沿折线 BCD 从点 B 开始运动到点 D使运动 的路程为 x，ADP 的面积为 y，那么 y 与 x 之间的函数关系的图象大致是（ ） 【答案】D 【解析】当点 P 在 BC 段时 0 x3，此时ADP 的面积不变， 1 3 23 2 y ，当点 P 在 CD 段时 3x4 （当点 P 运动到点 D 时不构成三角形） ， 1315 3 (32) 222 yxx ， 所以 3(03) 315 (34) 22 x y xx ， 故答案选 D 4. (2019枣庄) 如图,一直线与两坐标轴的正半轴分别交于 A,B 两点,P 是线段 AB 上任意一点(不包括端点),过点
17、 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为 8,则该直线的函数表达式是（ ） A.yx+4 B.yx+4 C.yx+8 D.yx+8 【答案】A 【解析】由题可知,矩形 ONPM 中,ON+NP+PM+MO8,OM+ON4,设 P(x,y),则 x+y4,即 yx+4,故选 A. 5. （2019自贡）均匀的向一个容器内注水，在注满水的过程中，水面的高度 h 与时间 t 的函数关系如图所示， 则该容器是下列四个中的（ ） 【答案】D. 【解析】解：由图象可知，高度 h 随时间 t 的变换规律是先快后慢. D 选项的底面积由小变大，水面高度随时间变换符合先快后慢. 故选 D. 6.（
18、2019衢州）如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿EADC移动至终点 C.设P点经过的路径长为x，CPE的面积为y，则下列图象能大致反映y与x函数关系的是（ ） 【答案】C 【解析】当点 P 在线段 AE 上时，即当 0x2 时，SCPE= 1 2 EPBC= 1 2 x4=2x；当点 P 在线段 AD 上时，即当 2x6 时，SCPE= S正方形ABCD- SBEC- SAPE- SPDC=44- 1 2 42- 1 2 2(x-2)- 1 2 4(6-x)=x+2，图象 为向上倾斜的线段；当点 P 在线段 DC 上时，即当 6x的解集为 . 【答案】x化为
19、3kx-6k0，3kx6k，因为 k0，所以 x2故答案为 x2 2. （2019 滨州） 如图， 直线 ykx+b （k0） 经过点 A （3， 1） ， 当 kx+b 1 3 x 时， x 的取值范围为_ 【答案】x3 【解析】当 x=3 时， 1 3 x= 1 3 3=1，点 A 在一次函数 y= 1 3 x 的图象上，且一次函数 y= 1 3 x 的图象经过第一、 三象限，当 x3 时，一次函数 y= 1 3 x 的图象在 y=kx+b 的图象上方，即 kx+b 1 3 x 3. (2019泰安)在平面直角坐标系中,直线 l:yx+1 与 y 轴交于点 A1,如图所示,依次作正方形 O
20、A1B1C1,正方形 y x C 16题图 E D B AO y x C 16题图 E B F D AO x y x y O -6 O O O BC A A B B A P E F C1A2B2C2,正方形 C2A3B3C3,正方形 C3A4B4C4,点 A1,A2,A3,A4,在直线上,点 C1,C2,C3,C4,在 x 轴正 半轴上,则前 n 个正方形对角线长的和是_. 【答案】2n22 【解析】点 A1是 yx+1 与 y 轴的交点,A1(0,1),OA1B1C1是正方形,C1(1,0),A1C1 2,A2(1,2),C1A2 2,A2C222,A3C24,A3C342,按照此规律,An
21、Cn2n 1 2,前 n 个正方形对角线长的和为:2+22 +4 2+2n 1 22(1+2+4+2n 1) 2(1+1+2+4+2n 11) 2(2n1)2n22. 4. （2019 潍坊）当直线(22 )3yk xk经过第二、三、四象限时，则 k 的取值范围是 【答案】1k3 【解析】直线经过第二、三、四象限，所以 220, 30 k k ，解得：1k3 5. （2019乐山）如图，在四边形ABCD中，ADBC， 30B，线ABl .当直线l沿射线BC方向， 从点B开始向右平移时，直线l与四边形ABCD的边分别相交于点E、F.设直线l向右平移的距离为x，线段 EF的长为y，且y与x的函数关
22、系如图所示，则四边形ABCD的周长是 . 图 图 【答案】10+2 3 【解析】过 A 作 AGl 交 BC 于 G, 过 C 作 CHl 交 AD 于 H， 由图象可知，BG=4,CG=AH=1，DH =7-5=2， 30B，ABl .，AG = 1 2 BG=2，cosB= 3 2 AB BG ，AB=23， AGl,CHl ， CHAG，又AGB=90-B=60，HCG=AGB=60， 又ADBC，DHC=HCB=60,又 CH=DH=2，所以CHD 是等边三角形， CD=DH=2，四边形ABCD的周长=AB+BG+GC+AH+DH+DC=23+4+1+1+2+2=10+23. 6.（2
23、019攀枝花）正方形 A1B1C1A2，A2B2C2A3，A3B3C3A4，按如图所示的方式放置，点 A1，A2，A3，和点 B1， B2， B3， 分别在直线 ykxb （k0） 和 x 轴上。 已知 A1（0， 1） ， 点 B1（1， 0） ， 则 C5的坐标是 . l F E D C A B 【答案】（47,16） 【解析】如图， C1（2，1），C2（5，2），C 3（11，4），C 4（23，8）， C1的横坐标：221, 纵坐标：120, C2的横坐标：52220, 纵坐标：221, C3的横坐标：11232120, 纵坐标：422, C4的横坐标：2324222120, 纵坐标
24、：823, 依此类推，C5的横坐标：252322212047, 纵坐标：1624, C5（47,16）. 7. （2019天津）直线 y=2x-1 与 x 轴交点坐标为 【答案】 （ 2 1 ，0） 【解析】直线与 x 轴的交点即当 y=0 时，x 的值为 2 1 ，所以答案为（ 2 1 ，0） 【知识点】一次函数与二元一次方程，坐标轴的点的坐标的特点. 8. （2019金华）元朝朱世杰的算学启蒙一书记载：“今有良马日行二百四十里，驽马日行一百五十里，驽 马先行一十二日，问良马几何日追及之”，如图是两匹马行走路程 ts 关于行走时间 t 的函数图象，则两图象交点 P 的坐标是_. x y A4
25、 C3 B3 A3 C2 A2 B2 C1 B1 A1 O x y A4 C3 B3 A3 C2 A2 B2 C1 B1 A1 O t（日） s(里) P 12 O 【答案】 （32，4800） 【解析】设良马 t 日追之,根据题意，得 240 , 150(12 , st st ）解得 20, 4800. t s 故答案为（32，4800） 9.（2019重庆 B 卷）一天，小明从家出发匀速步行去学校上学，几分钟后，在家休假的爸爸发现小明忘带数学 书， 于是爸爸立即匀速跑步去追小明， 爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的 5/4 快步赶往学 校，并在从家出发后 23 分钟到校（
26、小明被爸爸追上时交流时间忽略不计）.两人之间相距到达路程 y（米）与小 明从家出发到学校的步行时间 x（分钟）之间的函数关系如图所示，则小明家到学校的路程为 米. 【答案】2080 米 【解析】小明被爸爸追上以前的速度为 x 米/分钟， 爸爸的速度为 y 米/分钟， 由题意得：11x = 5y 解得 x=80 55 4 x+5y=1380 y=176 小明家到学校的路程为： 11 80+（23-11）5 4 80 =880+1200 = 2080（米） 23 （2019 山东省德州市，23，12）下表中给出 A，B，C 三种手机通话的收费方式 收费方式 月通话费/元 包时通话时间/h 超时费/
27、（元/min） A 30 25 0.1 B 50 50 0.1 C 100 不限时 （1）设月通话时间为 x 小时，则方案 A，B，C 的收费金额 y1，y2，y3都是 x 的函数，请分别求出这三个函数 解析式 （2）填空： 若选择方式 A 最省钱，则月通话时间 x 的取值范围为 ； 若选择方式 B 最省钱，则月通话时间 x 的取值范围为 ； 若选择方式 C 最省钱，则月通话时间 x 的取值范围为 ； （3）小王、小张今年 5 月份通话费均为 80 元，但小王比小张通话时间长，求小王该月的通话时间 【解题过程】 （1）0.1 元/min6 元/h， 由题意可得， y1， y2， y3100（x
28、0） ； （2）作出函数图象如图： 17题图题图 0111623 1380 x/分钟分钟 y/米米 结合图象可得： 若选择方式 A 最省钱，则月通话时间 x 的取值范围为：0 x， 若选择方式 B 最省钱，则月通话时间 x 的取值范围为：x， 若选择方式 C 最省钱，则月通话时间 x 的取值范围为：x 故答案为：0 x，x，x （3）小王、小张今年 5 月份通话费均为 80 元，但小王比小张通话时间长， 结合图象可得：小张选择的是方式 A，小王选择的是方式 B， 将 y80 分别代入 y2，可得 6x25080， 解得：x55， 小王该月的通话时间为 55 小时 25 （2019淮安）快车从甲
29、地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶， 途中快车体息 1.5 小时，慢车没有休息.设慢车行驶的时间为 x 小时，快车行校的路程为 1 y千米，慢车行驶的路 程为 2 y千米.下图中折线 OAEC 表示 1 y与 x 之间的函数关系，线段 OD 表示 2 y与 x 之间的函数关系. 请解答下判问题： (1)求快车和慢车的速度； (2)求图中线段 EC 所表示的 1 y与 x 之间的函数表达式； (3)线段 OD 与线段 EC 相交于点 F，直接写出点 F 的坐标，并解释点 F 的实际意义. 第 25 题图 【解题过程】 （1）1802=90，1803=60， 快
30、车的速度为 90km/h，慢车的速度 60km/h； （2）途中快车体息 1.5 小时， 点 E（3.5，180）. （360-180）90=2， 点 C（5.5，360）. 设 EC 的解析式为bkxy 1 ， 则 3605 . 5 1805 . 3 bk bk ， 135 90 b k ， 13590 1 xy. （3）慢车的速度为 60km/h， OD 的解析式为 y=60 x. 由 13590 60 xy xy 得， 270 2 9 y x ， 点 F 的坐标为（270 2 9， ）. 点 F 的实际意义：慢车行驶的时间为 2 9 小时，第二次背快车追上，此时两车的行程均为 270km
31、. 10. （2019重庆 A 卷）某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落 在公司，无法联系，于是乙匀速骑车去追赶甲乙刚出发 2 分钟时，甲也发现自己手机落在公司，立刻按原 路原速骑车回公司，2 分钟后甲遇到乙，乙把手机给甲后立即原路原速返回公司，甲继续原路原速赶往某小 区送物件，甲乙两人相距的路程 y（米）与甲出发的时间 x（分钟）之间的关系如图所示（乙给甲手机的时 间忽略不计）则乙回到公司时，甲距公司的路程是 米 【答案】6000 【解析】由图象可知甲 8 分钟行驶 4000 米，甲速为 500 米/分，而甲乙两人 2 分钟行驶的路程和为甲 10 分钟
32、行 驶的路程，故乙速为(500105002)41000 米/分，于是 400045006000 米，即为乙回到公司时，甲 距公司的路程，因此答案为 6000 三、解答题 23(2019泰州)小李经营一家水果店,某日到水果批发市场批发一种水果,经了解,一次性批发这种水果不得少于 100kg,超过 300kg时,所有这种水果的批发单价均3元/kg,图中拆线表示批发单价 y(元/kg)与质量 x(kg)的函数关系. 求图中线段 AB 所在直线的函数表达式; 小李用 800 元一次可以批发这种水果的质量是多少? 第 23 题图 x y (kg) (元元/kg) B A 5 3 300100 O 【解题
33、过程】(1)由图可得,点 A(100,5),B(300,3),设线段 AB 表达式为 ykx+b,则 5100 3300 kb kb ,解之得: 0.01 6 k b , 所以 y0.01x+6(100 x300); (2)设批发 xkg,则单价为(0.01x+6)元,根据题意可列方程:(0.01x+6)x800,解之得:x1200,x2400(舍去),所以小 李用 800 元一次可以批发这种水果的质量为 200kg. 18 （2019 年浙江省绍兴市，第 18 题，8 分 ）如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 y（千 瓦时）关于已行驶路程 x（千米）的函数图象. （1）根据
34、图象，直接写出蓄电池剩余电量为 35 千瓦时时汽车已行驶的路程，当1500 x时，求 1 千瓦时的 电量汽车能行驶的路程； （2）当200150 x时求 y 关于 x 的函数表达式，并计算当汽车已行驶 180 千米时，蓄电池的剩余电量. 【分析】 （1）由图象可知，蓄电池剩余电量为 35 千瓦时时汽车已行驶了 150 千米，据此即可求出 1 千瓦时的 电量汽车能行驶的路程； （2）运用待定系数法求出 y 关于 x 的函数表达式，再把 x180 代入即可求出当汽车已行驶 180 千米时，蓄 电池的剩余电量 解： （1）由图象可知，蓄电池剩余电量为 35 千瓦时时汽车已行驶了 150 千米 1 千
35、瓦时的电量汽车能行驶的路程为：千米. （2）设 ykx+b（k0） ，把点（150，35） ， （200，10）代入， 得，y0.5x+110， 当 x180 时，y0.5180+11020. 答：当 150 x200 时，函数表达式为 y0.5x+110，当汽车已行驶 180 千米时，蓄电池的剩余电量为 20 千瓦时 22 （2019山东省青岛市，22，10分）某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售 量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示. （1）求该商品每天的销售量y与销售单价x之间的函数关系式； （2）若商店按单价不低于成本价，且不高
36、于50元销售，则销售单价定为多少，才能使销售该商品每天获得的利 润w（元）最大？最大利润是多少？ （3）若商店要使销售该商品每天获得的利润不低于800元，则每天的销售量最少应为多少件？ 【解题过程】解： （1）设y与销售单价x之间的函数关系式为：ykxb， 将点(30,100)、(45,70)代入一次函数表达式得： 10030 7045 kb kb ， 解得： 2 160 k b ， 故函数的表达式为：2160yx ； （2）由题意得： 2 (30)( 2160)2(55)1250wxxx， 20 ，故当55x 时，w随x的增大而增大，而3050 x剟， 当50 x 时，w由最大值，此时，12
37、00w ， 故销售单价定为 50 元时，该超市每天的利润最大，最大利润 1200 元； （3）由题意得：(30)( 2160) 800 xx， 解得：70 x， 每天的销售量2160 20yx ， 每天的销售量最少应为 20 件 17 （2019 江西省，17，6 分）如图，在平面直角坐标系中，点 A、B 的坐标分别为( 2 3 ，0） ， （ 2 3 ，1） ，连 接 AB，以 AB 为边向上作等边三角形 ABC. (1)求点 C 的坐标； (2)求线段 BC 所在直线的解析式. 【解题过程】 （1）如图所示，作 BDx 轴于点 D， 点 A、B 的坐标分别为( 2 3 ，0） ， （ 2
38、3 ，1） ， AD= 2 3 ) 2 3 (=3，BD=1， 21)3( 2222 BDADAB, 3 3 3 1 tan AD BD BAD, BAD=30. ABC 是等边三角形， BAC=60，AC=AB=2， CAD=BAD+BAC=30+60=90， 点 C 的坐标为( 2 3 ，2） ； （2）设线段 BC 所在直线的解析式为 y=kx+b， 点 C、B 的坐标分别为( 2 3 ，2） ， （ 2 3 ，1）, 1 2 3 2 2 3 bk bk ，解得 2 3 3 3 b k ， 线段 BC 所在直线的解析式为： 2 3 3 3 xy. 19 （2019山西）某游泳馆推出了两种
39、收费方式. 方式一:顾客先购买会员卡,每张会员卡 200 元,仅限本人一年使用,凭卡游泳,每次游泳再付费 30 元. 方式二:顾客不购买会员卡,每次游泳付费 40 元. 设小亮在一年内来此游泳馆的次数为 x 次,选择方式一的总费用为 y1(元),选择方式二的总费用为 y2(元). (1)请分别写出 y1,y2与 x 之间的函数表达式. (2)小亮一年内在此游泳馆游泳的次数 x 在什么范围时,选择方式一比方式二省钱. 【解题过程】(1)y130 x+200,y240 x (2)由 y1y2,得 30 x+30020,当 x20 时,选择方式一比方式二省钱. 21 （2019常德）某生态体验园推出
40、了甲、乙两种消费卡，设入园次数为 x 时所需费用为 y 元，选择这两种卡 消费时，y 与 x 的函数关系如图 5 所示，解答下列问题： （1）分别求出选择这两种卡消费时，y 关于 x 的函数表达式； （2）请根据入园次数确定选择哪种卡消费比较合算 解： （1）设 y甲kx，把（5，100）代入得 1005k，k20，y甲20 x. 设 y乙k1x+b1，把（0，100）和（20，300）分别代入得 1 11 100 20300 b kb ，解得 1 1 100 10 b k ，y乙10 x+100. （2）y乙10 x+100 与 y甲20 x 联立解得 B（10，200） ， 当 0 x10
41、 时，y甲y乙，即选择甲种消费卡合算； 当 x10 时，y甲y乙，即选择乙种消费卡合算 1. （2019重庆 A 卷）在初中阶段的函数学习中，我们经历了“确定函数的表达式利用函数图象研究其性 质运用函数解决问题”的学习过程在画函数图象时，我们通过描点或平移的方法画出了所学的函数图 象同时，我们也学习了绝对值的意义 )0( )0( aa aa a 结合上面经历的学习过程，现在来解决下面的问题：在函数bkxy3中，当 x2 时，y4；当 x0 时，y1 x（次） y(元） 300 05 图5 C B A 乙 甲 100 20 （1）求这个函数的表达式； （2）在给出的平面直角坐标系中，请用你喜欢的
42、方法面出这个函数的图象并写出这个函数的一条性质； （3）已知函数 y 1 2 x3 的图象如图所示，结合你所画的函数图象，直接写出不等式3 2 1 3xbkx的 解集 【思路分析】 （1）利用待定系数法，将 x2 时，y4；x0 时，y1 代入函数关系式，得到关于 k、b 的二元一次方程组，解之即可 （2）利用绝对值意义将所求带有绝对值的函数转化为分段函数，即可在所给 网格的平面直角系中画出该函数的图象，并结合图象较易从增减性上写出该函数的性质； （3）利用数形结合 思想，由两个函数图象的交点的横坐标分别为 1 和 4，分段函数图象在直线 y 1 2 x3 下方的自变量 x 的取 值范围即为所
43、求不等式的解集体 【解题过程】 （1）由题意得 234 31 kb b ，解得 3 2 4 k b ，故该函数解析式为 y 3 3 2 x4 （2）当 x2 时，该函数为 y 3 2 x7；当 x2 时，该函数为 y 3 2 x1，其图象如下图所示： 性质：当 x2 时，y 随 x 的增大而增大；当 x2 时，y 随 x 的增大而减小 （3）不等式3 2 1 3xbkx的解集为 1x4 【知识点】一次函数的图象与性质；分类函数；绝对值；待定系数法；不等式的解集；数形结合思想 2. （2019重庆 B 卷）函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索 第 23 题
44、答图 y x O -1 -2-3-4-5-6-7-8 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 86 5 432 1 y x O -1 -2-3-4-5-6-7-8 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 86 5 432 1 第 23 题图 画函数2yx 的图象，经历分析解析式、列表、描点、连线过程得到函数图象如下图所示；经历同样的过程 画函数22yx和22yx的图象如右图所示. (1)观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解析式中绝对值前面的系数相同， 则图象的开口方向和形状完全相同， 只有最高点和对称轴发生了变化.写
45、出点 A， B 的坐标和函数22yx的 对称轴； (2)探索思考：平移函数2yx 的图象可以得到函数22yx和22yx的图象，分别写出平移的方 向和距离； (3)拓展应用：在所给的平面直角坐标系内画出函数231yx 的图象.若点( 1 x， 1 y)和( 2 x， 2 y)在该函数图 象上，且 2 x 1 x3，比较 1 y、 2 y的大小. 【思路分析】 （1）A 点的坐标是x=0 时函数22yx的值，代入即可求出；B 点的坐标是y=0 时函数 22yx的值，代入即可求得；观察函数22yx的图象即可得到对称轴； （2）根据函数2yx 顶点坐标 O（0，0）和函数22yx的顶点坐标 A；根据函
46、数2yx 顶点坐标 O （0，0）和函数22yx的顶点坐标 B； （3）根据函数图象的性质可推断出 1 y, 2 y. 也可用特值法求解： 2 x 1 x 1 x可以取 4， 2 x可以231yx 1 y=-1， 2 y=-3， 1 y 2 y. 【解题过程】解： （1）当x=0，222022yx ， 当y=0 时，220 x，x=-2，2x 22yx2x； （2）22yx是由2yx 向上平移 2 个单位长度得到的，22yx是由2yx 向左平移 2 个单 位长度得到的. （3）231yx 是由2yx 向右平移 3 个单位长度，向上平移 1 个单位长度得到的， 123 4 5 687 3 2 1
47、 -1 -2 -3 -4-5-6 -8 -9 -7 -6 -5 -4 -3 -2 -1 x y y=-2x+2 y=-2x y=-2x+2 x y -3 -2 -10 123 -6 -4-2 0-2 -4 -6 O A B 其顶点坐标为（3，1） ，对称轴为3x ，在对称轴的右侧，函数图象呈下降趋势， y随x的增大而减小， 2 x 1 x3, 1 y 2 y. 【知识点】新函数的应用；函数的性质；函数图象的画法； 3. (2019台州)如图 1,某商场在一楼到二楼之间设有上,下行自动扶梯和步行楼梯.甲,乙两人从二楼同时下行,甲乘 自动扶梯,乙走步行楼梯,甲离一楼地面的高度 h(单位:m)与下行时间 x(单位:s)之间具有函数关系 h 3 10 x+6,乙 离一楼地面的高度 y(单位:m)与下行时间 x(单位:s)的函数关系如图 2 所示. (1)求 y 关于 x 的函数关系式; (2)请通过计算说明甲,乙两人谁先到达一楼地面. 【思路分析】(1)用待定系数法得到解析式;(2)令函数值为零,求出两人到达一层的时间,比较可得结论. 【解题过程】(1)设 ykx+b,将(0,6),(15,3)代入 6 315 b kb ,k 1 5 ,b6,y 1 5 x+6. (2)对于甲:令
