1、 一、选择题一、选择题 9 （20192019长沙）长沙）如图，RtABC 中，C=90，B=30，分别以点 A 和点 B 为圆心，大于 1 2 AB 的长为半径 作弧，两弧相交于 M、N 两点，作直线 MN，交 BC 于点 D，连接 AD，则CAD 的度数是（ ） A20 B30 C45 D60 【答案答案】B 【解析】【解析】在ABC 中，B=30，C=90，BAC=180-B-C=60，由作图可知 MN 为 AB 的中垂线， DA=DB，DAB=B=30，CAD=BAC-DAB=30，故本题选：B 8 （2019烟台）烟台）已知60AOB，以 O 为圆心，以任意长为半径作弧，交 OA，O
2、B 于点 M，N，分别以 M，N 为圆心，以大于 1 2 MN的长度为半径作弧，两弧在AOB内交于点 P，以 OP 为边作15POC， 则BOC的度数为（ ） A15 B45 C15或30 D15或45 【答案答案】D 【解析】【解析】 由题目可以得出 OP 为AOB的平分线， 所以 1 30 2 AOPBOPAOB ， 又因为15POC， 考 虑 到 点 C 有 可 能 在A OP内 也 有 可 能 在B OP内 ， 所 以 当 点 C 在AOP内 时BOC 45BOPPOC，当点 C 在BOP内时BOC15BOPPOC 三、解答题三、解答题 22 （2019 山东省德州市，山东省德州市，2
3、2，12）如图，BPD120，点 A、C 分别在射线 PB、PD 上，PAC30，AC 2 （1）用尺规在图中作一段劣弧，使得它在 A、C 两点分别与射线 PB 和 PD 相切要求：写出作法，并保留 作图痕迹； （2）根据（1）的作法，结合已有条件，请写出已知和求证，并证明； （3）求所得的劣弧与线段 PA、PC 围成的封闭图形的面积 【解题过程】【解题过程】 （1）如图， （2）已知：如图，BPD120，点 A、C 分别在射线 PB、PD 上，PAC30，AC2，过 A、C 分 别作 PB、PD 的垂线，它们相交于 O，以 OA 为半径作O，OAPB， 求证：PB、PC 为O 的切线； 证明
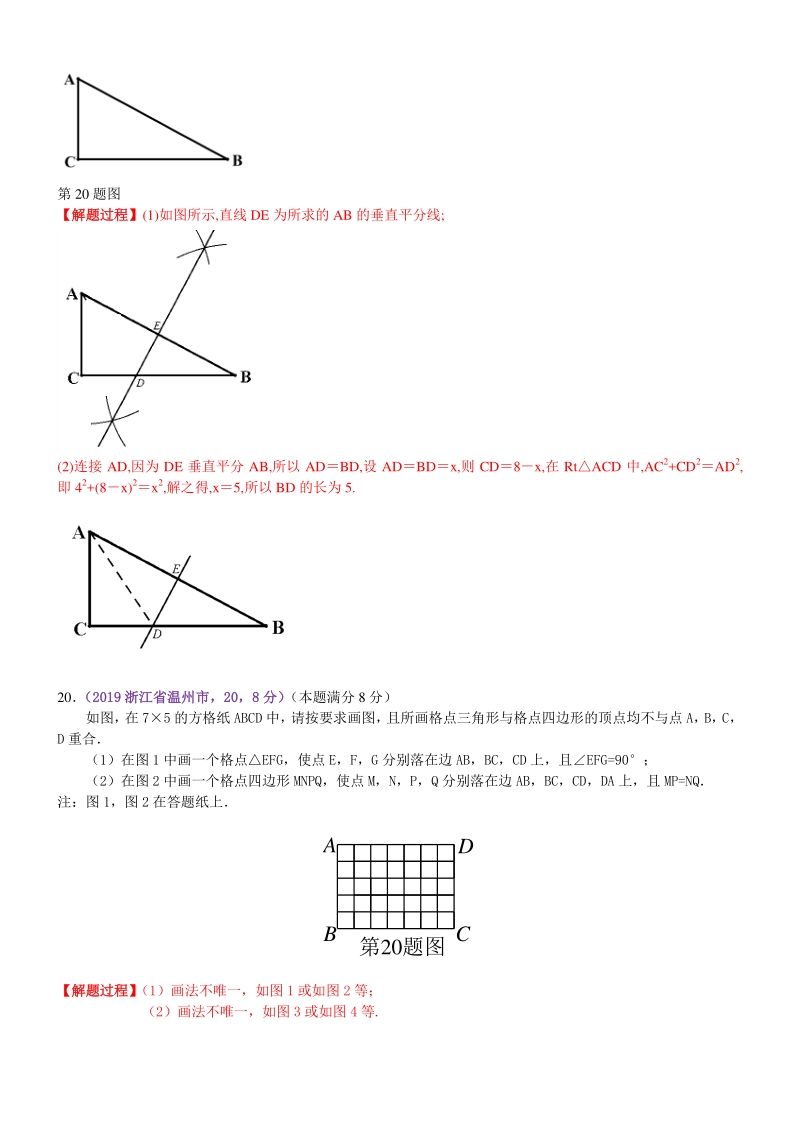
4、：BPD120，PAC30， PCA30， PAPC， 连接 OP， OAPA，PCOC， PAOPCO90， OPOP， RtPAORtPCO（HL） OAOC， PB、PC 为O 的切线； （3）OAPOCP903060， OAC 为等边三角形， OAAC2，AOC60， OP 平分APC， APO60， AP22，劣弧 AC 与线段 PA、PC 围成的封闭图形的面积S四边形APCOS扇形AOC2 2242 20(2019泰州泰州)如图,ABC 中,C90, AC4, BC8. (1)用直尺和圆规作 AB 的垂直平分线; (保留作图痕迹,不要求写作法) (2)若(1)中所作的垂直平分线交
5、BC 于点 D,求 BD 的长. 第 20 题图 【解题过程】【解题过程】(1)如图所示,直线 DE 为所求的 AB 的垂直平分线; (2)连接 AD,因为 DE 垂直平分 AB,所以 ADBD,设 ADBDx,则 CD8x,在 RtACD 中,AC2+CD2AD2, 即 42+(8x)2x2,解之得,x5,所以 BD 的长为 5. 20 （20192019 浙江省温州市，浙江省温州市，2020，8 8 分）分） （本题满分 8 分） 如图， 在 75 的方格纸 ABCD 中， 请按要求画图， 且所画格点三角形与格点四边形的顶点均不与点 A， B， C， D 重合 （1）在图 1 中画一个格点
6、EFG，使点 E，F，G 分别落在边 AB，BC，CD 上，且EFG=90； （2）在图 2 中画一个格点四边形 MNPQ，使点 M，N，P，Q 分别落在边 AB，BC，CD，DA 上，且 MP=NQ 注：图 1，图 2 在答题纸上 【解题过程】【解题过程】 （1）画法不唯一，如图 1 或如图 2 等； （2）画法不唯一，如图 3 或如图 4 等. 第20题图 D CB A 图 1 图 2 图 3 图 4 20 （2019嘉兴）嘉兴）在 66 的方格纸中，点A，B，C都在格点上，按要求画图： （1）在图 1 中找一个格点D，使以点A，B，C，D为顶点的四边形是平行四边形 （2）在图 2 中仅用
7、无刻度的直尺，把线段AB三等分（保留画图痕迹，不写画法） 【解题过程】【解题过程】解： （1）由勾股定理得： CDABCD，BDACBD， ADBCAD； 画出图形如图 1 所示； （2）如图 2 所示 21 （2019 江苏盐城卷，江苏盐城卷，21，8 如图，AD 是ABC 的角平分线 （1） 作线段 AD 的垂直平分线 EF，分别交 AB、AC 于点 E、F; (用直尺和圆规作图，标明字母，保留作图痕迹，不写作法) （2） 连接 DE、DF，四边形 AEDF 是_形 （直接写出答案） 【解题过程】【解题过程】 E F G A BC D G F E A BC D Q P N M A BC D
8、 M N P Q A BC D （1） 如图所示：直线 EF 就是线段 AD的垂直平分线 （2） 菱形 证明：连结 DE、DF EF 垂直平分 AD EA=ED,FA=FD EAD=EDA, FAD=FDA AD 是BAC 的平分线 EAD=FAD EAD=EDA=FAD=FDA AEDF,AFED 四边形 AEDF 为平行四边形 EA=ED 四边形 AEDF 为菱形 15 （2019青岛）已知： ， 直线 l 及 l 上两点 A, B. 求作：RtABC ，使点 C 在直线 l 的上方，且ABC= 90 , BAC 【解题过程】如国所示： 则 RtABC 即为所求. 15 （2019 江西省
9、，江西省，15，6 分）分）在在ABC 中，中，ABAC，点，点 A 在以在以 BC 为直径的半圆内，请仅用无刻度的直尺分为直径的半圆内，请仅用无刻度的直尺分 别按下列要求画图别按下列要求画图(保留画图痕迹保留画图痕迹). (1)在图在图 1 中作弦中作弦 EF，使，使 EFBC； (2)在图在图 2 中以中以 BC 为边作一个为边作一个 45的圆周角的圆周角. 【解题过程】解： （【解题过程】解： （1）如图所示）如图所示 DE 即为所求. （2）如图所示）如图所示 MBC 即为所求. 21 （2019陇南）陇南）已知：在ABC 中，ABAC （1）求作：ABC 的外接圆 （要求：尺规作图，
10、保留作图痕迹，不写作法） （2）若ABC 的外接圆的圆心 O 到 BC 边的距离为 4，BC6，则 S O 解： （解： （1 1）如图）如图O O即为所求即为所求 （2 2）设线段）设线段BCBC的垂直平分线交的垂直平分线交BCBC于点于点E E 由题意可知，由题意可知，OEOE4 4，BEBEECEC3 3， 在在 RtRtOBEOBE中，中，OBOB5 5， S S圆圆O O 5 5 2 2 2525 故答案为故答案为 2525 1.（2019济宁）济宁）如图，点 M 和点 N 在AOB 内部 （1）请你作出点 P，使点 P 到点 M 和点 N 的距离相等，且到AOB 两边的距离也相等（
11、保留作图痕迹，不写 作法） ； （2）请说明作图理由 解解： (1) 画出AOB 的角平分线，画出线段 MN 的垂直平分线，两者的交点就得到 P 点 （2）作图的理由：点 P 在AOB 的角平分线上，又在线段 MN 的垂直平分线上，AOB 的角平分线和线段 MN 的垂直平分线的交点即为所求 2 （2019无锡）按要求作图，不要求写作法，但要保留作图痕迹 （1）如图 1，A 为圆 O 上一点，请用直尺（不带刻度）和圆规作出得内接正方形； （2）我们知道，三角形具有性质，三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交 于一点，事实上，三角形还具有性质：三条高交于同一点，请运用上
12、述性质，只用直尺（不带刻度）作图： 如图 2，在ABCD 中，E 为 CD 的中点，作 BC 的中点 F； 图 3，在由小正方形组成的网格中，的顶点都在小正方形的顶点上，作ABC 的高 AH. 解：解： （1） 连结 AE 并延长交圆 E 于点 C，作 AC 的中垂线交圆于点 B，D，四边形 ABCD 即为所求. （2）连结 AC，BD 交于点 O，连结 EB 交 AC 于点 G，连结 DG 并延长交 CB 于点 F， F 即为所求. A E E C A B D A C B 一、选择题一、选择题 8 （2019深圳）如图，已知 AB=AC，AB=5，BC=3以 AB 两点为圆心，大于 1 2
13、AB 的长为半径画弧，两弧 相交于点 M，N，过 M，N 作直线与 AC 相交于点 D，则BDC 的周长为（ ） A8 B10 C11 D13 【答案】A 【 解 析 】 由 作 图 方 法 知 ， MN是 线 段AB的 垂 直 平 分 线 ， AD=BD ， BDC的 周 长 =BD+DC+BC=AD+DC+BC=5+3=8故选 A 【知识点】尺规作图；线段的垂直平分线；等腰三角形 9 （2019 河南）如图，在四边形 ABCD 中，ADBC，D=90，AD=4，BC=3，分别以点 A，C 为圆心， 大于 1 2 AC 长为半径作弧，两弧交于点 E，作射线 BE 交 AD 于点 F，交 AC
14、 于点 O，若点 O 是 AC 的中点， 则 CD 的长为（ ） A. 2 2 B.4 C.3 D. 10 【答案】A 【解题过程】过点 A 做 BMBC 与点 M, ADBC BCD+D=180 又D=90BCD=90 BCD=D=BMD=90 四边形 BCDM 为矩形 AB=BC=3 BM=CD 由作图可知 AE=CE 又O 是 AC 的中点 AB=BC=3 在 RtABM 中，AMB=90，AM=AD-MD=1 BM= 2222 312 2ABAM CD= 2 2.故选 A 【知识点】尺规作图 矩形的判定及性质 等腰三角形的性质 垂直平分线的性质 勾股定理 10.（2019宜昌）通过如下
15、尺规作图，能确定点 D 是 BC 边中点的是（ ） 【答案】【答案】A 【解析】【解析】作线段 BC 的垂直平分线可得线段 BC 的中点 由此可知：选项 A 符合条件，故选：A 【知识点】【知识点】作图题 10. （2019河北）根 F E O B A D C M F E O B D A C 据圆规作图的痕迹，可用直尺成功找到三角形外心的是（ ） 【答案】C 【解析】外心是三角形三边中垂线的交点，而 C 中的作图是找两边的中垂线，C 正确. 【知识点】【知识点】尺规作图、中垂线的作图、外心的定义尺规作图、中垂线的作图、外心的定义 二、填空题二、填空题 16 （2019兰州）如图，矩形兰州）如图
16、，矩形 ABCD，BAC=60，以点，以点 A 为圆心，以任意长为半径作弧分别交 为圆心，以任意长为半径作弧分别交 AB，AC 于于 点点 M,N 两点， 再分别以点两点， 再分别以点 M,N 为圆心， 以大于为圆心， 以大于 2 1 MN 的长作半径作弧交于点的长作半径作弧交于点 P， 作射线， 作射线 AP 交交 BC 于点于点 E， 若若 BE=1，则矩形，则矩形 ABCD 的面积等于的面积等于 . 【答案】【答案】3 3 【解【解析析】 在矩形】 在矩形 ABCD 中， 中， BAC=60， ， B=90， ， BCA=30， ， AE 平分平分BAC， ， BAE=EAC=30， 在
17、在 RtABE 中，中，BE=1，AE= 1 sin30 =2，AB= 1 3 tan30 ，EAC=ECA=30，EC=AE=2， S矩形矩形ABCD=AB BC=3 3. 【知识点】【知识点】矩形的性质，角平分线的性质，矩形的面积，锐角三角函数矩形的性质，角平分线的性质，矩形的面积，锐角三角函数 三、解答题三、解答题 23. （2019广州)如图，O 的直径 AB10，弦 AC8，连接 BC （1）尺规作图：作弦 CD，使 CDBC（点 D 不与 B 重合） ，连接 AD； （保留作图痕迹，不写作法） （2）在（1）所作的图中，求四边形 ABCD 的周长 【思路分析】 （1）以 C 为圆心
18、，CB 为半径画弧，交O 于 D，线段 CD 即为所求 （2）连接 BD，OC 交于点 E，设 OEx，构建方程求出 x 即可解决问题 【解题过程】解： （1）如图，线段 CD 即为所求 （2）连接 BD，OC 交于点 E，设 OEx AB 是直径， ACB90， BC= 2 2= 102 82=6， BCCD， = ， OCBD 于 E BEDE， BE2BC2EC2OB2OE2， 62（5x）252x2， 解得 x= 7 5， BEDE，BOOA， AD2OE= 14 5 ， 四边形 ABCD 的周长6+6+10+ 14 5 = 124 5 【知识点】作图题； 圆周角定理；解直角三角形 2
19、0 （2019 福建）已知ABC 为和点 A，如图. (1)以点 A为一个顶点作ABC，使ABCABC，ABC的面积等于ABC 面积的 4 倍； (尺规作图， 不写作法，保留作图痕迹) (2)设 D、E、F 分别是ABC 三边 AB、BC、AC 的中点，D、E、F分别是你所作的ABC三边 AB、BC、 CA的中点，求证：DEFDEF. 【思路分析】 （1）利用相似三角形面积比等于相似比平方，作ABC使ABC的各边是ABC 中各边的 2 倍； （2）利用三角形中位线定理，结合相似三角形对应边成比例，可得DEF 的各边与DEF的各边对应成比 A C BA 例，即可得出结论. 【解题过程】 （1）如
20、图： 则ABC为所求作图形. (2)证明：D、E、F 分别是ABC 三边 AB、BC、AC 的中点，DE=AC，EF=AB，FD=BC，同理，DE= AC， EF=AB， FD=BC， ABCABC， =， =， 即=，DEFDEF. 【知识点】尺规作图；相似三角形性质与判定；三角形中位线 24. （2019 宿迁）在 RtABC 中，C90 （1）如图，点 O 在斜边 AB 上，以点 O 为圆心，OB 长为半径的圆交 AB 于点 D，交 BC 于点 E，与边 AC 相 切于点 F求证：12； （2）在图中作M，使它满足以下条件： 圆心在边 AB 上；经过点 B；与边 AC 相切 （尺规作图，
21、只保留作图痕迹，不要求写出作法） 【思路分析】 （1）连接 OF，可证得 OFBC，结合平行线的性质和圆的特性可求得1OFB2，可得出 结论； （2）由（1）可知切点是ABC 的角平分线和 AC 的交点，圆心在 BF 的垂直平分线上，由此即可作出M 【解题过程】解： （1）证明：如图，连接 OF， C A B C B A 1 2 1 2 1 2 1 2 1 2 1 2 AC A C AB A B BC B C 1 2 1 2 AC A C 1 2 1 2 AB A B 1 2 1 2 BC B C DE D E EF E F FD F D AC 是O 的切线， OEAC， C90， OEBC，
22、 1OFB， OFOB， OFB2， 12 （2）如图所示M 为所求 作ABC 平分线交 AC 于 F 点， 作 BF 的垂直平分线交 AB 于 M，以 MB 为半径作圆， 即M 为所求 证明：M 在 BF 的垂直平分线上， MFMB， MBFMFB， 又BF 平分ABC， MBFCBF， CBFMFB， MFBC， C90， FMAC， M 与边 AC 相切 【知识点】作图题；与圆有关的位置关系 19 （2019广东） 如图，在 ABC 中，点D是边AB上的一点. （1）请用尺规作图法，在 ABC 内，求作 ADE ，使 ADEB ，DE交AC于E； （不要求写作法，保留 作图痕迹） （2）
23、在（1）的条件下，若 2 AD DB ，求 AE EC 的值. 【思路分析】 （1）尺规作一个角等于已知角； （2）根据平行线的判定和性质求解。 【解题过程】解： （1）如图. （2） ADEB ， /DEBC. ADEABC . 2 AEAD ECDB . 【知识点】尺规作图 平行线的判定和性质 17 （2019陕西） （5 分）如图，在ABC 中，ABAC，AD 是 BC 边上的高请用尺规作图法，求作ABC 的 外接圆 （保留作图痕迹，不写作法） 【分析】作线段 AB 的垂直平分线，交 AD 于点 O，以 O 为圆心，OB 为半径作O，O 即为所求 【解答】解：如图所示：O 即为所求 【点
24、评】本题考查作图复杂作图，等腰三角形的性质，三角形的外接圆与外心等知识，解题的关键是熟练 掌握基本知识，属于中考常考题型 20. （2019甘肃）如图，在ABC中，点P是AC上一点，连接BP，求作一点M，使得点M到AB和AC两 边的距离相等，并且到点B和点P的距离相等 （不写作法，保留作图痕迹） 【思路分析】【思路分析】根据角平分线的作法、线段垂直平分线的作法作图即可 【解题过程】解：如图，点M即为所求， 【知识点】线段垂直平分线的性质；角平分线的性质 21. （2019武威）已知：在ABC中，ABAC （1）求作：ABC的外接圆 （要求：尺规作图，保留作图痕迹，不写作法） （2）若ABC的外
25、接圆的圆心O到BC边的距离为 4，6BC ，则 O S 【思路分析】【思路分析】（1）作线段AB，BC的垂直平分线，两线交于点O，以O为圆心，OB为半径作O，O即为 所求 （2）在Rt OBE中，利用勾股定理求出OB即可解决问题 【解题过程】（1）如图，O即为所求 （2）设线段BC的垂直平分线交BC于点E 由题意4OE ，3BEEC， 在Rt OBE中， 22 345OB， 2 525 O S 圆 故答案为25 【知识点】等腰三角形的性质；三角形的外接圆与外心 17. （2019菏泽）如图，四边形 ABCD 是矩形 （1）用尺规作线段 AC 的垂直平分线，交 AB 于点 E，交 CD 于点 F
26、（不写作法，保留作图痕迹） ； （2）若 BC4，BAC30，求 BE 的长 【思路分析】【思路分析】（1）根据线段的垂直平分线的作图解答即可； （2）利用含 30的直角三角形的性质解答即可 【解题过程】解：（1）如图所示： （2）四边形 ABCD 是矩形，EF 是线段 AC 的垂直平分线， AEEC，CABACE30， ECB60， ECB30， BC4， BE= 43 3 【知识点】【知识点】矩形的性质；线段垂直平分线的性质；作图 一、选择题一、选择题 5 （2019 北京）北京） 已知锐角AOB，如图， （1）在射线 OA 上取一点 C，以点 O 为圆心，OC 长为半径作，交射线 OB
27、于点 D，连接 CD； （2）分别以点 C，D 为圆心，CD 长为半径作弧，交于点 M，N； （3）连接 OM，MN 根据以上作图过程及所作图形，下列结论中错误的是 ACOM=COD B若 OM=MN，则AOB=20 CMNCD DMN=3CD 【答案答案】D【解析】【解析】由作图知，CMCDDN ,OM=OC=OD=ON； A在中，由CMCD得COM=COD；故选项 A 正确. B由 OM=MN，结合 OM=ON 知OMN 为等边三角形；得MON=60.又由CMCDDN得COM=COD= DON；AOB=20.故选项 B 正确. C由题意知 OC=OD， 180 2 COD OCD . 设
28、OC 与 OD 与 MN 分别交于 R，S.易得MORNOS （ASA） OR=OS 180 2 COD ORS OCDORS MNCD. 故选项 C 正确. D由CMCDDN得 CM=CD=DN=3CD；而由两点之间线段最短得 CM+CD+DNMN，即 MN3CD；MN=3CD N M D OB C P Q A 是错误的；故选 D. 【知识点】【知识点】全等三角形的性质和判定、圆的有关性质、等边三角形的性质和判定. 7 （2019襄阳）如图，分别以线段 AB 的两个端点为圆心，大于 AB 的一半的长为半径画弧，两弧分别交于 C， D 两点，连接 AC，BC，AD，BD，则四边形 ADBC 一
29、定是( ) A正方形 B矩形 C梯形 D菱形 答案：D 解析：本题考查尺规作图以及菱形的判定.由作图可知，半径相等，可知 AC=AD=BC=BD，四条边相等的四边形 是菱形.选项 D 正确 8 （2019新疆）如图，在ABC 中，C=90，A=30，以点 B 为圆心，适当长为半径画弧，分别交 BA，BC 于点 M， N； 再分别以点 M、 N 为圆心，大于 1 2 MN 的长为半径画弧， 两弧交于点 P，作射线 BP 交 AC 于点 D则 下列说法中不正确的是（ ） ABP 是ABC 的平分线 BAD=BD CSCBDSABD=13 DCD= 1 2 BD 答案：C 解析：本题考查了含有 30
30、角的直角三角形以及尺规作图， 由画法可知 BP 是ABC 的平 分线，选项 A 正确； C=90，A=30，ABC=60 BP 是ABC 的平分线，ABP=DBC=A=30 AD=BDCD 选项 B 正确； DBC=30， CD= 1 2 BD选项 D 正确； CD= 1 2 BD，BD=AD， CDAD=1：2 BCD 与ACD 具有相同的高 BC， SCBDSABD=12选项 C 不正确，因此本题选 C 7.(2019东营)如图，在 RtABC 中，ACB=90 ，分别以点 B 和点 C 为圆心，大于 2 1 BC 的长为半径作弧，两 弧相交于 D、 E 两点， 作直线 DE 交 AB 于
31、点 F， 交 BC 于点 G， 连结 CF， 若 AC=3， CG=2， 则 CF 的长为 （ ） A 2 5 B3 C2 D 2 7 答案：A 解析：由作图可知，DE 是边 BC 的垂直平分线，那么 BC=2CG=4，在 RtABC 中，由勾股定理，可得 AB=5. 因为ACB=90 ，所以 DEAC，因为 G 为 BC 中点，所以 F 为 AB 中点，所以 CF= 2 1 AB= 2 5 因此本题选 A 7 （2019郴州）如图，分别以线段 AB 的两端点 A，B 为圆心，大于 1 2 AB 长为半径画弧，在线段 AB的两侧分 别交于点 E，F，作直线 EF 交 AB 于点 O在直线 EF
32、 上任取一点 P（不与 O重合），连接 P A，PB，则下列结论不一定 成立的是 AP APB BOAOB COPOF DPOAB 答案：C 解析：本题考查了线段垂直平分线的性质；作图复杂作图，由作图过程可知 EF 是 AB 的垂直平分线，所以 PA PB，OAOB，POAB，一定成立，因此本题选 C （2019包头）如图，在 Rt ABC 中，B90 ，以点 A 为圆心，适当长为半径画弧，分别交 AB 于点 D、E，再 分别过点 D、 E 为圆心， 大于 2 1 DE 的长为半径画弧， 两弧交于点 F， 作射线 AF 交边 BC 于点 G， 若 BG1， AC=4， 则 ACG 的面积是（）
33、 A1 B 2 3 C2 D 2 5 （第 7 题图） O F E AB P 答案：C 【解析】 本题考查了角平分线的尺规作图， 角平分线性质的应用及三角形面积的计算， 由尺规作图知， AF 是BAC 的角平分线，所以 ACG 边 AC 上的高即是点 G 到 AC 的距离BG，故其面积为 2 1 BG AC= 2 1 1 4=2，因 此本题选 C 9 （2019安顺）安顺） 如图，在菱形 ABCD 中，按以下步骤作图： 分别以点 C 和点 D 为圆心，大于 2 1 CD 为半径作弧，两弧交于点 M，N 两点； 作直线 MN，且 MN 恰好经过点 A，与 CD 交于点 E，连接 BE，则下列说法
34、错误的是（ ） AABC60 BSABE2SADE C若 AB4，则 BE47 DsinCBE 14 21 【答案答案】C 【解析】【解析】由作法得 AE 垂直平分 CD，AED90，CEDE， 四边形 ABCD 为菱形，AD2DE， DAE30，D60， ABC60，所以 A 选项的说法正确； AB2DE，SABE2SADE，所以 B 选项的说法正确； 作 EHBC 于 H，如图，若 AB4， 在 RtECH 中，ECH60，CHCE1，EH3CH3， 在 RtBEH 中，BE27，所以 C 选项的说法错误； sinCBE BE EH 72 3 14 21 ，所以 D 选项的说法正确 故选：
35、C 【知识点】【知识点】三角形的面积；线段垂直平分线的性质；菱形的性质；基本作图（作一条线段等于已知线段；作一个 角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线） ；解直角三角形菁 优 7. （2019长春）长春）如图，在 ABC 中，ACB 为钝角。用直尺和圆规在边 AB 上确定一点 D. 使ADC=2B， 则符合要求的作图痕迹是 第 9 题图 第9题答图 【答案】【答案】B 【解答过程】【解答过程】ADC=2B，且ADC=B+BCD， B=BCD， 点 D 在线段 BC 的垂直平分线上， 故选 B 【知识点】【知识点】线段垂直平分线的性质；作图复杂作图 二
36、、填空题二、填空题 15. （2019本溪）本溪）如图，BD 是矩形 ABCD 的对角线，在 BA 和 BD 上分别截取 BE，BF，使 BE=BF；分别以 E，F 为圆心，以大于 1 2 EF 的长为半径作弧，两弧在ABD 内交于点 G，作射线 BG 交 AD 于点 P，若 AP=3， 则点 P 到 BD 的距离为 . 【答案】【答案】3. 【解析】【解析】过点 P 作 PQBD，垂足为 Q， 根据题意可得 BP 平分ABD. 四边形 ABCD 为矩形， A=90 ， PA=PQ. PA=3， PQ=3， 故答案为 3. 【知识点】【知识点】角平分线的性质. 三、解答题三、解答题 18 （2
37、019仙桃）请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹 (1)如图，四边形ABCD中，AB=AD，B=D，画出四边形ABCD的对称轴m； (2)如图，四边形ABCD中，ADBC，A=D，画出BC边的垂直平分线n 解析：本题考查了轴对称的性质以及垂直平分线的性质 （1）根据条件可知 AB=AD,BC=BD,所以 A 点和 C 点都 在线段 BD 的垂直平分线上，即过 A、C 两点的直线为四边形 ABCD 的对称轴； （2）延长 BA 和 CD 交于 E 点， 根据条件可得 BE=CE，即 E 在 BC 的垂直平分线上，连接 AC、BD 相交于 F 点， 可得 BF=CF，即 F 点在
38、 BC 的垂直平分线上，所以过点 E、F 的直线为 BC 边的垂直平分线. 答案：解：(1)过 A、C 两点作直线 AC，即为对称轴 m; 延长 BA、CD，交于点 E，连接 AC、BD，交于点 F， 过 E、F 两点画直线 EF，即为 BC 边的垂直平分线 n. 20 （2019 柳州）柳州）已知：AOB 求作：AOB，使得AOBAOB 作法： 以 O 为圆心，任意长为半径画弧，分别交 OA，OB 于点 C，D； 画一条射线 OA，以点 O为圆心，OC 长为半径画弧，交 OA于点 C； 以点 C为圆心，CD 长为半径画弧，与第步中所画的弧相交于点 D； 过点 D画射线 OB，则AOBAOB
39、根据上面的作法，完成以下问题： （1）使用直尺和圆规，作出AOB（请保留作图痕迹） （2）完成下面证明AOBAOB 的过程（注：括号里填写推理的依据） 证明：由作法可知 OCOC，ODOD，DC ， CODCOD（ ） AOBAOB （ ） 【解题过程】解题过程】 （1）如图所示，AOB即为所求； （2）证明：由作法可知 OCOC，ODOD，DCDC， CODCOD（SSS） AOBAOB （全等三角形的对应角相等） 故答案为：DC，SSS，全等三角形的对应角相等 【知识点】【知识点】尺规作图，全等三角形的判定和性质 5. （2019荆州）如图，矩形 ABCD 的顶点 A，B，C 分别落在MO
40、N 的边 OM，ON 上，若 OAOC，要求只 用无刻度的直尺作MON 的平分线小明的作法如下：连接 AC，BD 交于点 E，作射线 OE，则射线 OE 平 分MON有以下几条几何性质：矩形的四个角都是直角，矩形的对角线互相平分，等腰三角形的 “三线合一” 小明的作法依据是（ ） A B C D 【答案】【答案】C 【解析】【解析】解：四边形 ABCD 为矩形， AECE， 而 OAOC， OE 为AOC 的平分线 故选：C 【知识点】【知识点】等腰三角形的性质；矩形的性质；作图基本作图 25. （2019 台湾）如图的ABC中，ABACBC，且D为BC上一点今打算在AB上找一点P，在AC 上
41、找一点Q，使得APQ与PDQ全等，以下是甲、乙两人的作法： （甲)连接AD，作AD的中垂线分别交AB、AC于P点、Q点，则P、Q两点即为所求 （乙)过D作与AC平行的直线交AB于P点，过D作与AB平行的直线交AC于Q点，则P、Q两点即为所求 对于甲、乙两人的作法，下列判断何者正确？( ) A两人皆正确 B两人皆错误 C甲正确，乙错误 D甲错误，乙正确 【答案】【答案】A 【解析】【解析】解：如图 1，PQ垂直平分AD， PAPD，QAQD， 而PQPQ， ()APQDPQ SSS ，所以甲正确； 如图 2，/ /PDAQ，/ /DQAP， 四边形APDQ为平行四边形， PADQ，PDAQ， 而
42、PQQP， ()APQDQP SSS ，所以乙正确 故选：A 【知识点】【知识点】全等三角形的判定；线段垂直平分线的性质；作图 20. （2019赤峰）已知：AC 是ABCD 的对角线 （1）用直尺和圆规作出线段 AC 的垂直平分线，与 AD 相交于点 E，连接 CE （保留作图痕迹，不写作法） ； （2）在（1）的条件下，若 AB3，BC5，求DCE 的周长 解：（1）如图，CE 为所作； （2）四边形 ABCD 为平行四边形， ADBC5，CDAB3， 点 E 在线段 AC 的垂直平分线上， EAEC， DCE 的周长CE+DE+CDEA+DE+CDAD+CD5+38 【知识点】线段垂直平
43、分线的性质；平行四边形的性质；作图基本作图 20. （2019孝感） 如图，RtABC 中，ACB=90，一同学利用直尺和圆规完成如下操作： 以点 C 为圆心，以 CB 为半径画弧，交 AB 于点 G；分别以点 G、B 为圆心，以大于GB 2 1 的长为半径画弧， 两弧交点 K，作射线 CK； 以点 B 为圆心，以适当的长为半径画弧，交 BC 于点 M，交 AB 的延长线于点 N；分别以点 M、N 为圆心， 以大于 2 1 MN 的长为半径画弧，两弧交于点 P，作直线 BP 交 AC 的延长线于点 D,交射线 CK 于点 E. 请你观察图形，根据操作结果解答下列问题； (1) 线段 CD 与
44、CE 的大小关系是 .（3 分） (2)过点 D 作 DFAB 交 AB 的延长线于点 F，若 AC=12，BC=5，求 tanDBF 的值.（5 分） 解析：本题考查了尺规作图及全等三角形的判定,勾股定理,三角函数的计算等知识 (1)由作图知CEAB,又DFAB,BP平分CBF, BCDBFD,由平行线及角平分线的性质得到CD=CE; (2)由勾股定理求得 AB,由三角函数求得 CD,DF,BC,BF 的值. 答案：解： （1）CD 与 CE 的大小关系是相等. （2）BD 平分CBF，BCCD，BFDF，BC=BF，CBD=FBD 在BCD 和BFD 中， DCB= DFB CBD= FBD BD=BD BCDBFD（AAS）CD=DF. 设 CD=DF=x,在 RtACB 中，AB= 22 ACBC=13 sinDAF= DFBC ADAB ， 5 1213 x x ，x= 15 2 BC=BF=5，tanDBF= DF AD = 15 2 1 5 = 3 2 .
