1、2019-2020 学年浙江省温州市瑞安市八年级（上）期末数学试卷学年浙江省温州市瑞安市八年级（上）期末数学试卷 一、选择题（本题有一、选择题（本题有 10 小题，每小题小题，每小题 3 分共分共 30 分分.每小题只有一个选项是正确的，不选多选、错选均每小题只有一个选项是正确的，不选多选、错选均 不得分）不得分） 1 （3 分）下列各组数可能是一个三角形的边长的是（ ） A5，7，12 B5，6，7 C5，5，12 D1，2，6 2 （3 分）在平面直角坐标系中，点（3，4）所在的象限是（ ） A第一象限 B第二象限 C第三象限 D第四象限 3 （3 分）下列图案中是轴对称图形的是（ ） A
2、 B C D 4 （3 分）一次函数 y2x+2 的图象与 x 轴的交点坐标是（ ） A （0，2） B （0，2） C （1，0） D （1，0） 5 （3 分）对于命题“若 ab，则 a2b2” ，能说明它属于假命题的反例是（ ） Aa2，b1 Ba1，b2 Ca2，b1 Da1，b1 6 （3 分）直线 y2x+b 上有三个点（2.4，y1） ， （1.5，y2） ， （1.3，y3） ，则 y1，y2，y3的大小关系是 （ ） Ay1y2y3 By1y2y3 Cy2y1y3 Dy2y1y3 7 （3 分）如图，ABCDCB要说明ABCDCB，需添加的条件不能是（ ） AABDC BAD
3、 CBMCM DACDB 8 （3 分）如图，在 RtABC 中，C90，AD 是BAC 的平分线，若 AC6，BC8，则 SABD：S ACD为（ ） A5：3 B5：4 C4：3 D3：5 9 （3 分）若不等式组的解集为 xa，则下列各式中正确的是（ ） Aa+b0 Ba+b0 Cab0 Dab0 10 （3 分）意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞“，从而巧妙 的证明了勾股定理小明用两张全等的的纸片和拼成如图 1 所示的图形，中间的六边形 ABCDEF 由两个正方形和两个全等的直角三角形组成 已知六边形 ABCDEF 的面积为 28， S正方形ABGF
4、： S正方形CDEG 4： 1 小明将纸片翻转后拼成如图 2 所示的图形， 其中BAF90， 则四边形 BCEF 的面积为（ ） A16 B20 C22 D24 二、填空题（本题有二、填空题（本题有 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 11 （3 分）若 a 的 3 倍与 2 的差是负数，则可列出不等式 12 （3 分）把点 A（3，1）先向右平移 2 个单位，再向上平移 3 个单位，所得点的坐标为 13 （3 分）在 RtABC 中，ABC90，D 为斜边 AC 的中点，BD5则 AC 14 （3 分）点 A（m，1）关于 y 轴的对称点恰好落在一次函数 y3x+
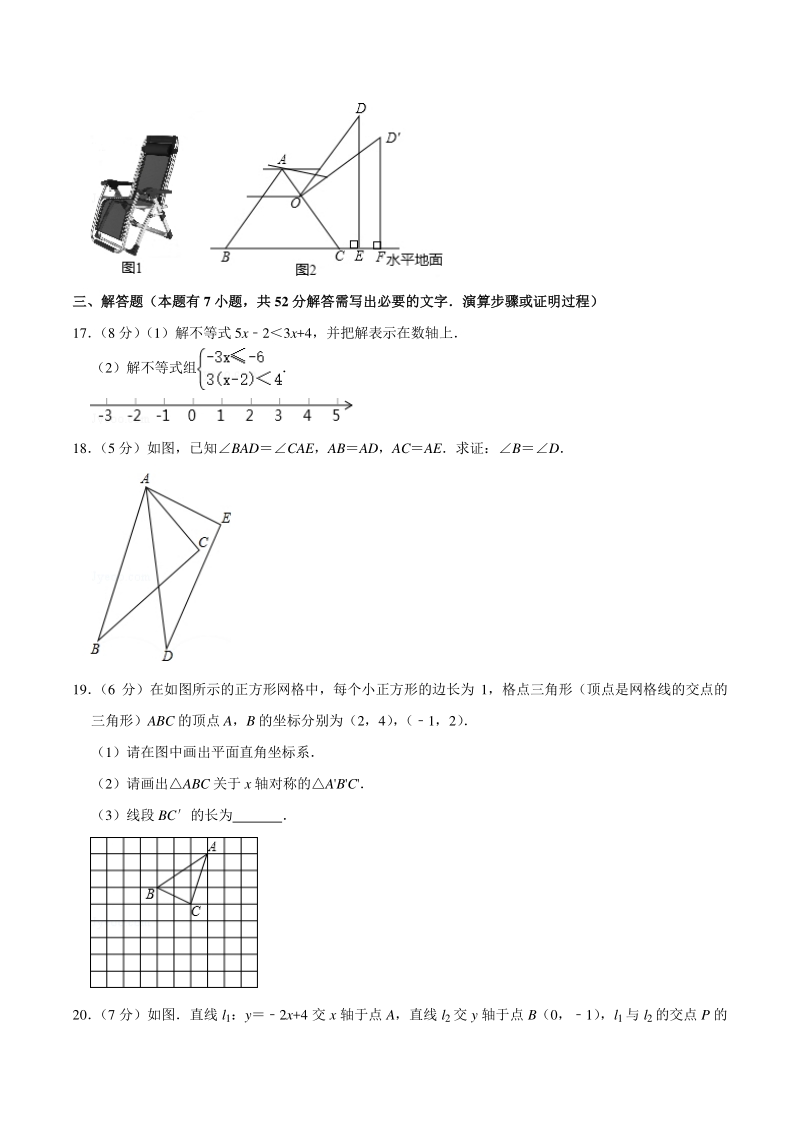
5、4 的图象上，则 m 15 （3 分）如图，在 RtABC 中，C90，D，E 分别为边 AB，AC 上一点，ADAE将ABC 沿 DF 折叠， 使点 B 与 E 重合， 折痕交边 BC 于点 F 若CEF 为等腰三角形， 则A 的度数为 度 16 （3 分）图 1 是小慧在“天猫双 11”活动中购买的一张多档位可调节靠椅，档位调节示意图如图 2 所 示，已知两支脚 ABAC10 分米，BC12 分米，O 为 AC 上固定连接点，靠背 OD10 分米档位为 档时，ODAB档位为档时，ODAC当靠椅由档调节为档时，靠背頂端 D 向后靠的水平 距离（即 EF）为 分米 三、解答题（本题有三、解答题
6、（本题有 7 小题，共小题，共 52 分解答需写出必要的文字演算步骤或证明过程）分解答需写出必要的文字演算步骤或证明过程） 17 （8 分） （1）解不等式 5x23x+4，并把解表示在数轴上 （2）解不等式组 18 （5 分）如图，已知BADCAE，ABAD，ACAE求证：BD 19 （6 分）在如图所示的正方形网格中，每个小正方形的边长为 1，格点三角形（顶点是网格线的交点的 三角形）ABC 的顶点 A，B 的坐标分别为（2，4） ， （1，2） （1）请在图中画出平面直角坐标系 （2）请画出ABC 关于 x 轴对称的ABC （3）线段 BC的长为 20 （7 分）如图直线 l1：y2x+
7、4 交 x 轴于点 A，直线 l2交 y 轴于点 B（0，1） ，l1与 l2的交点 P 的 横坐标为 1连结 AB （1）求直线 l2的函数表达式， （2）求PAB 的面积 21 （7 分）如图，在等腰 RtABC 中，BAC90，延长 BA 至点 D，连结 DC，过点 B 作 BEDC 于 点 E，F 为 BC 上一点，FCFE连结 AF，AE （1）求证：FAFE （2）若D60，BC10，求AEF 的周长 22 （8 分）某甜品店用 A，B 两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如 表所示该店制作甲款甜品 x 份，乙款甜品 y 份，共用去 A 原料 2000
8、克 款式 原料 A 原料（克） B 原料（克） 甲款甜品 30 15 乙款甜品 10 20 （1）求 y 关于 x 的函数表达式 （2）已知每份甲甜品的利润为 5 元，每份乙甜品的利润为 2 元，假设两款甜品均能全部卖出若获得总 利润不少于 360 元，则至少要用去 B 原料多少克？ 23 （11 分）如图直线 y2x+4 分别与 x 轴，y 轴交于点 AB，过点 B 的直线 yx+b 交 x 轴于点 C， D 为 OC 的中点P 为射线 BC 上一动点，连结 PA，PD，过 D 作 DEAP 于点 E （1）直接写出点 A，D 的坐标：A（ ， ） ，D（ ， ） （2）当 P 为 BC 中
9、点时，求 DE 的长 （3）当ABP 是以 AP 为腰的等腰三角形时，求点 P 坐标 （4）当点 P 在线段 BC（不与 BC 重合）上运动时，作 P 关于 DE 的对称点 P，若 P落在 x 轴上， 则 PC 的长为 2019-2020 学年浙江省温州市瑞安市八年级（上）期末数学试卷学年浙江省温州市瑞安市八年级（上）期末数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（本题有一、选择题（本题有 10 小题，每小题小题，每小题 3 分共分共 30 分分.每小题只有一个选项是正确的，不选多选、错选均每小题只有一个选项是正确的，不选多选、错选均 不得分）不得分） 1 （3 分）下列各组数
10、可能是一个三角形的边长的是（ ） A5，7，12 B5，6，7 C5，5，12 D1，2，6 【分析】根据三角形三边关系定理逐个判断即可 【解答】解：A、5+712，不符合三角形三边关系定理，不能组成三角形，故本选项不符合题意； B、5+67，5+76，6+75，符合三角形三边关系定理，能组成三角形，故本选项符合题意； C、5+512，不符合三角形三边关系定理，不能组成三角形，故本选项不符合题意； D、1+26，不符合三角形三边关系定理，不能组成三角形，故本选项不符合题意； 故选：B 【点评】本题考查了三角形的三边关系定理，能熟记三角形的三边关系定理的内容是解此题的关键，注 意：三角形的任意两
11、边之和都大于第三边 2 （3 分）在平面直角坐标系中，点（3，4）所在的象限是（ ） A第一象限 B第二象限 C第三象限 D第四象限 【分析】应先判断出点的横纵坐标的符号，进而判断点所在的象限 【解答】解：点的横坐标 30，纵坐标40， 点 P（3，4）在第四象限 故选：D 【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点四个象限的符号特点分别 是：第一象限（+，+） ；第二象限（，+） ；第三象限（，） ；第四象限（+，） 3 （3 分）下列图案中是轴对称图形的是（ ） A B C D 【分析】根据轴对称图形的概念判断即可 【解答】解：A、不是轴对称图形； B、不是轴对称图
12、形； C、不是轴对称图形； D、是轴对称图形； 故选：D 【点评】 本题考查的是轴对称图形的概念， 轴对称图形的关键是寻找对称轴， 图形两部分折叠后可重合 4 （3 分）一次函数 y2x+2 的图象与 x 轴的交点坐标是（ ） A （0，2） B （0，2） C （1，0） D （1，0） 【分析】把 y0 代入一次函数的解析式中即可求出与 x 轴的交点坐标 【解答】解：把 y0 代入 y2x+2， x1， 一次函数与 x 轴的交点坐标为（1，0） 故选：C 【点评】本题考查一次函数与 x 轴的交点坐标问题，解题的关键是将 y0 代入一次函数解析式中即可求 出答案本题属于基础题型 5 （3 分
13、）对于命题“若 ab，则 a2b2” ，能说明它属于假命题的反例是（ ） Aa2，b1 Ba1，b2 Ca2，b1 Da1，b1 【分析】反例就是符合已知条件但不满足结论的例子，可据此判断出正确的选项 【解答】解：对于命题“若 ab，则 a2b2” ，能说明它属于假命题的反例是 a1，b2，ab， 但（1）2（2）2， 故选：B 【点评】此题主要考查了反证法的意义，在假设结论不成立时要注意考虑结论的反面所有可能的情况， 如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定 6 （3 分）直线 y2x+b 上有三个点（2.4，y1） ， （1.5，y2） ， （1.3，y3） ，则
14、 y1，y2，y3的大小关系是 （ ） Ay1y2y3 By1y2y3 Cy2y1y3 Dy2y1y3 【分析】由 k20，利用一次函数的性质可得出 y 值随 x 值的增大而减小，结合2.41.51.3 可得出 y1y2y3，此题得解 【解答】解：k20， y 值随 x 值的增大而减小 又2.41.51.3， y1y2y3 故选：A 【点评】本题考查了一次函数的性质，牢记“k0，y 随 x 的增大而增大；k0，y 随 x 的增大而减小” 是解题的关键 7 （3 分）如图，ABCDCB要说明ABCDCB，需添加的条件不能是（ ） AABDC BAD CBMCM DACDB 【分析】根据全等三角形
15、的判定定理逐个判断即可 【解答】解：A、在ABC 和DCB 中 ABCDCB（SAS） ，故本选项不符合题意； B、在ABC 和DCB 中 ABCDCB（AAS） ，故本选项不符合题意； C、MBMC， MBCMCB， ABCDCB， ABMDCM， 在ABM 和DCM 中 ABMDCM（ASA） ， ABDC， 在ABC 和DCB 中 ABCDCB（SAS） ，故本选项不符合题意； D、根据ABCDCB，BCCB，ACBD 不能推出ABCDCB，故本选项符合题意； 故选：D 【点评】本题考查了全等三角形的判定和性质，能灵活运用定理进行推理是解此题的关键，注意：全等 三角形的判定定理有 SAS
16、，ASA，AAS，SSS 8 （3 分）如图，在 RtABC 中，C90，AD 是BAC 的平分线，若 AC6，BC8，则 SABD：S ACD为（ ） A5：3 B5：4 C4：3 D3：5 【分析】作 DEAB，根据角平分线的性质得到 DEDC，根据三角形的面积公式计算，得到答案 【解答】解：作 DEAB 于点 E， 由勾股定理得，AB10 AD 是BAC 的平分线，C90，DEAB， DEDC， SABDABDE，SACDACDC， SABD：SACDAB：AC10：65：3， 故选：A 【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键 9 （3
17、分）若不等式组的解集为 xa，则下列各式中正确的是（ ） Aa+b0 Ba+b0 Cab0 Dab0 【分析】 根据不等式组的解集为 xa，可得：ab，据此判断出各式中正确的是哪个即可 【解答】解：不等式组的解集为 xa， ab， a+b0 故选：B 【点评】此题主要考查了不等式的解集的求法，要熟练掌握，解答此题的关键是要明确：同大取大，同 小取小，大大小小没有解，大小小大取中间 10 （3 分）意大利文艺复兴时期的著名画家达芬奇利用两张一样的纸片拼出不一样的“空洞“，从而巧妙 的证明了勾股定理小明用两张全等的的纸片和拼成如图 1 所示的图形，中间的六边形 ABCDEF 由两个正方形和两个全等
18、的直角三角形组成 已知六边形 ABCDEF 的面积为 28， S正方形ABGF： S正方形CDEG 4： 1 小明将纸片翻转后拼成如图 2 所示的图形， 其中BAF90， 则四边形 BCEF 的面积为（ ） A16 B20 C22 D24 【分析】根据正方形的性质得到 GBGF，GCGE，BGFCGE90，根据全等三角形的性质得 到 BCEF，BCBFFEEC， 设 BCEFc，证得四边形 BCEF是菱形， BCc，推出四边形 BCEF是正方形，设 S正方形ABGF4m，S正方形CDEG1m，根据六边形 ABCDEF 的面积为 28，列方程即可得到结论 【解答】解：四边形 ABGF、四边形 C
19、DEG 是正方形， GBGF，GCGE，BGFCGE90， BGCFGE90， 在BGC 和FGE 中， BGCFGE（SAS） ， 同理可证BGCBAFEDC， BCEF，BCBFFEEC，设 BCEFc， 四边形 BCEF是菱形，BCc， DEFAFE，OEFAFB， BFE90， 四边形 BCEF是正方形， S正方形ABGF：S正方形CDEG4：1， 设 S正方形ABGF4m，S正方形CDEG1m， FG2，EG， 六边形 ABCDEF 的面积为 28， 4m+m+2228， m4， EF2， EFEF2， 四边形 BCEF的面积20， 故选：B 【点评】本题考查了勾股定理的证明，正方形
20、的判定和性质，全等三角形的判定和性质，正确的识别图 形是解题的关键 二、填空题（本题有二、填空题（本题有 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 11 （3 分）若 a 的 3 倍与 2 的差是负数，则可列出不等式 3a20 【分析】首先表示“a 的 3 倍与 2 的差” ，再表示“是负数”可得不等式 【解答】解：由题意得：3a20， 故答案为：3a20 【点评】此题主要考查了由实际问题抽象出一元一次不等式，关键是抓住关键词，选准不等号 12 （3 分）把点 A（3，1）先向右平移 2 个单位，再向上平移 3 个单位，所得点的坐标为 （5，2） 【分析】根据向左平移横坐
21、标减，向上平移，纵坐标加解答 【解答】解：点 A（3，1）向右平移 2 个单位，横坐标变为 3+25，向上平移 3 个单位，纵坐标变为 1+32， 所以所得点的坐标为（5，2） 故答案为（5，2） 【点评】 本题考查了利用平移解答坐标与图形的变化， 平移中点的变化规律是： 横坐标右移加， 左移减； 纵坐标上移加，下移减 13 （3 分）在 RtABC 中，ABC90，D 为斜边 AC 的中点，BD5则 AC 10 【分析】根据直角三角形斜边上的中线性质得出 AC2BD，代入求出即可 【解答】解：在 RtABC 中，ABC90，D 为斜边 AC 的中点，BD5， AC2BD2510， 故答案为：
22、10 【点评】本题考查了直角三角形斜边上的中线性质，能根据直角三角形斜边上的中线性质得出 AC2BD 是解此题的关键 14 （3 分）点 A（m，1）关于 y 轴的对称点恰好落在一次函数 y3x+4 的图象上，则 m 1 【分析】根据点 A 的坐标可找出点 A 关于 y 轴对称点的坐标，再利用一次函数图象上点的坐标特征可找 出关于 m 的一元一次方程，解之即可得出结论 【解答】解：点 A（m，1）关于 y 轴的对称点坐标为（m，1） 点（m，1）在一次函数 y3x+4 的图象上， 13m+4， m1 故答案为：1 【点评】本题考查了一次函数图象上点的坐标特征以及关于 x 轴、y 轴对称的点的坐
23、标，利用一次函数 图象上点的坐标特征，找出关于 m 的一元一次方程是解题的关键 15 （3 分）如图，在 RtABC 中，C90，D，E 分别为边 AB，AC 上一点，ADAE将ABC 沿 DF 折叠，使点 B 与 E 重合，折痕交边 BC 于点 F若CEF 为等腰三角形，则A 的度数为 30 度 【分析】如图，连接 BE设DBEDEBx用 x 的代数式表示A，B，根据A+B90构 建方程即可解决问题 【解答】解：如图，连接 BE设DBEDEBx 由翻折可知：FBFE，DBDE， FBEFEB，DBEDEB， CFCE，C90， CFE45， CFEFBE+FEB， FBEFEB22.5 AD
24、AE， ADEAEDDBE+DEB2x， A1804x， CBA+A90， 22.5+x+1804x90， 解得 x37.5， A180437.530， 故答案为 30 【点评】本题考查翻折变换，等腰三角形的性质，三角形内角和定理等知识，解题的关键是学会利用参 数构建方程解决问题 16 （3 分）图 1 是小慧在“天猫双 11”活动中购买的一张多档位可调节靠椅，档位调节示意图如图 2 所 示，已知两支脚 ABAC10 分米，BC12 分米，O 为 AC 上固定连接点，靠背 OD10 分米档位为 档时，ODAB档位为档时，ODAC当靠椅由档调节为档时，靠背頂端 D 向后靠的水平 距离（即 EF）
25、为 2 分米 【分析】过 A 作 AGBC 于点 G，过 O 作 OHBC 于 H，作 OMDF 于点 M，交 DE 于点 N，再次证 明全等：ABGDON，ACGODM，便可解决问题 【解答】解：过 A 作 AGBC 于点 G，过 O 作 OHBC 于 H，作 OMDF 于点 M，交 DE 于点 N，如 图所示， 则 OMHE，ONHE， ABAC10，BC12 BGCGBC6， AG， ABCD，BCOM， ABGDON， 在ABG 和DON 中， ， ABGDON（AAS） ， BGONHE6， ODAC DOM+MOC90， OMBC， MOCACG， ACG+CAG90， CAGDO
26、M， 在ACG 和ODM 中， ， ACGODM（AAS） ， AGOMHF8， EFHFHE862（dm） ， 故答案为：2 【点评】本题主要考查了全等三角形的性质与判定，勾股定理，等腰三角形的性质，关键是构造全等三 角形 三、解答题（本题有三、解答题（本题有 7 小题，共小题，共 52 分解答需写出必要的文字演算步骤或证明过程）分解答需写出必要的文字演算步骤或证明过程） 17 （8 分） （1）解不等式 5x23x+4，并把解表示在数轴上 （2）解不等式组 【分析】 （1）移项，合并同类项，系数化成 1 即可； （2）先求出每个不等式的解集，再求出不等式组的解集即可 【解答】解： （1）5
27、x23x+4， 5x3x4+2， 2x6， x3， 在数轴上表示不等式的解集为： ； （2） 解不等式得：x2， 解不等式得：x， 不等式组的解集为 2x 【点评】本题考查了解一元一次不等式，解一元一次不等式组，在数轴上表示不等式的解集的应用，题 目比较好，难度适中 18 （5 分）如图，已知BADCAE，ABAD，ACAE求证：BD 【分析】利用 SAS 判定ABCADE，再根据全等三角形的对应边相等，对应角相等，即可证得B D 【解答】证明：BADCAE， BACDAE ABAD，ACAE， ABCADE（SAS） BD 【点评】 本题考查三角形全等的判定与性质， 判定两个三角形全等的一般
28、方法有： SSS、 SAS、 AAS、 HL 注 意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对 应相等时，角必须是两边的夹角 19 （6 分）在如图所示的正方形网格中，每个小正方形的边长为 1，格点三角形（顶点是网格线的交点的 三角形）ABC 的顶点 A，B 的坐标分别为（2，4） ， （1，2） （1）请在图中画出平面直角坐标系 （2）请画出ABC 关于 x 轴对称的ABC （3）线段 BC的长为 【分析】 （1）根据顶点 A，B 的坐标，即可画出平面直角坐标系； （2）根据轴对称的性质作出各顶点关于 x 轴的对称点，再顺次连接即可； （3
29、）根据勾股定理进行计算即可得到线段 BC的长 【解答】解： （1）平面直角坐标系如图所示； （2）如图所示，ABC即为所求 （3）由勾股定理得，线段 BC的长为 故答案为： 【点评】本题考查的是作图轴对称变换以及勾股定理的运用，熟知关于 x 轴对称的点的坐标特点是解 答此题的关键 20 （7 分）如图直线 l1：y2x+4 交 x 轴于点 A，直线 l2交 y 轴于点 B（0，1） ，l1与 l2的交点 P 的 横坐标为 1连结 AB （1）求直线 l2的函数表达式， （2）求PAB 的面积 【分析】 （1）根据 l1的解析式求出 P 点的坐标，再设出 l2的解析式，利用待定系数法就可以求出
30、l2的解 析式 （2）设 l1交 y 轴于点 C，求出 A、C 点坐标，得到 BC 的长，再利用 SPABSABCSPBC求出PAB 的面积 【解答】解： （1）设点 P 坐标为（1，y） ， 代入 y2x+4，得 y2， 则点 P（1，2） 设直线 l2的函数表达式为 ykx+b， 把 P（1，2） 、B（0，1）分别代入 ykx+b， 得， 解得 k3，b1 所以直线 l2的函数表达式为 y3x1； （2）设 l1交 y 轴于点 C，如图 l1的解析式为 y2x+4， y0 时，x2；x0 时，y4， A（2，0） ，C（0，4） ， B（0，1） ， BC5， SPABSABCSPBC
31、【点评】本题考查待定系数法求直线的解析式，点的坐标，直线的交点坐标以及三角形的面积求得交 点坐标是解题的关键 21 （7 分）如图，在等腰 RtABC 中，BAC90，延长 BA 至点 D，连结 DC，过点 B 作 BEDC 于 点 E，F 为 BC 上一点，FCFE连结 AF，AE （1）求证：FAFE （2）若D60，BC10，求AEF 的周长 【分析】 （1）证明EBCBEF，得出 BFFEFC，在 RtBAC 中，AF 是斜边 BC 上的中线，即可 得出结论； （2） 易证ACD30， ABCACB45， 则ECFACD+ACB75， 由 （1） 得 FAFE， AF是斜边BC上的中线
32、， 得出AFBC， AFBC5， 由FCFE， 推出EFC1802ECF30， 得出AFE60，则AEF 是等边三角形，即可得出结果 【解答】 （1）证明：BEDC， EBC+ECBCEF+BEF90， FCFE， ECBCEF， EBCBEF， BFFEFC， 在 RtBAC 中，AF 是斜边 BC 上的中线， FAFC， FAFE； （2）解：D60，BAC90， ACD30， ABC 为等腰直角三角形， ABCACB45， ECFACD+ACB30+4575， 由（1）得：FAFE，AF 是斜边 BC 上的中线， AFBC，AFBC5， FCFE， EFC1802ECF18027530，
33、 AFE903060， AEF 是等边三角形， AEF 的周长3AF3515 【点评】本题考查了等腰直角三角形的性质、等腰三角形的判定与性质、直角三角形的性质、三角形内 角和定理、等边三角形的判定与性质等知识；熟练掌握直角三角形的性质，证明AEF 是等边三角形是 解题的关键 22 （8 分）某甜品店用 A，B 两种原料制作成甲、乙两款甜品进行销售，制作每份甜品的原料所需用量如 表所示该店制作甲款甜品 x 份，乙款甜品 y 份，共用去 A 原料 2000 克 款式 原料 A 原料（克） B 原料（克） 甲款甜品 30 15 乙款甜品 10 20 （1）求 y 关于 x 的函数表达式 （2）已知每
34、份甲甜品的利润为 5 元，每份乙甜品的利润为 2 元，假设两款甜品均能全部卖出若获得总 利润不少于 360 元，则至少要用去 B 原料多少克？ 【分析】 （1）根据甲、乙两种甜品所需 A 种原料及其总的消耗量得出 30 x+10y2000，变换成函数解析 式即可； （2）根据利润的要求 5x+2y360，与（1）中的关系求出变量 x 的范围，设用去 B 原料 m 克，可得 m 15x+20y15x+20（2003x）400045x，由一次函数的性质可求解 【解答】解： （1）由题可得，30 x+10y2000，即 y2003x， 故 y 关于 x 的函数表达式为 y2003x； （2）由题意可
35、得：5x+2y360， 5x+2（2003x）360， x40， 设用去 B 原料 m 克， m15x+20y15x+20（2003x）400045x， k45， m 随 x 的增大而减小， 当 x40 时， m 的最小值为 400045402200（克） 答：至少要用去 B 原料 2200 克 【点评】本题考查的是一次函数的应用，充分结合了方程、不等式的综合应用，学会利用函数求最值及 特殊解是解题的关键 23 （11 分）如图直线 y2x+4 分别与 x 轴，y 轴交于点 AB，过点 B 的直线 yx+b 交 x 轴于点 C， D 为 OC 的中点P 为射线 BC 上一动点，连结 PA，PD
36、，过 D 作 DEAP 于点 E （1）直接写出点 A，D 的坐标：A（ 2 ， 0 ） ，D（ 2 ， 0 ） （2）当 P 为 BC 中点时，求 DE 的长 （3）当ABP 是以 AP 为腰的等腰三角形时，求点 P 坐标 （4）当点 P 在线段 BC（不与 BC 重合）上运动时，作 P 关于 DE 的对称点 P，若 P落在 x 轴上， 则 PC 的长为 【分析】 （1）求出 A、B 的坐标，确定 BC 的表达式为：yx+4，D 为 OC 的中点，即可求解； （2）利用 SAPDAPDEADPD，即可求解； （3）分 APAB、APBP 两种情况，分别求解即可； （4）P 关于 DE 的对称
37、点 P，若 P落在 x 轴上，则点 P与点 A 重合，则 PDPD，即可求解 【解答】解： （1）直线 y2x+4 分别与 x 轴，y 轴交于点 AB， 令 x0，则 y4，令 y0，则 x2，故点 A、B 的坐标分别为： （2，0） 、 （0，4） ； 将点 B 的坐标代入 yx+b 并解得：b4， 故直线 BC 的表达式为：yx+4，故点 C（4，0） ，D 为 OC 的中点，故点 D（2，0） ； 故答案为：2，0，2，0； （2）P 为 BC 中点时，则点 P（2，2） ，而点 D（2，0） ，故 PDAC， SAPDAPDEADPD，即DE42， 解得：DE； （3）设点 P（m，4
38、m） ，而点 A、B 的坐标分别为： （2，0） 、 （0，4） ， 则 AP2（m+2）2+（4m）2，AB220，BP22m2， 当 APAB 时， （m+2）2+（4m）220，解得：m0（舍去）或 2； 当 APBP 时，同理可得：m5， 故点 P（2，2）或（5，1） ； （4）P 关于 DE 的对称点 P，若 P落在 x 轴上，则点 P与点 A 重合，即点 P（2，0） ， 则 PDPD，即（2+2）2（m2）2+（4m）2， 解得：m3（舍去 3+） ， 故点 P（3，1+） ，而点 C（4，0） ， 则 PC+， 故答案为 【点评】 本题考查的是一次函数综合运用， 涉及到一次函数的性质、 中点公式的运用、 勾股定理的运用、 面积的公式的运用等，其中（3） ，要注意分类求解，避免遗漏
