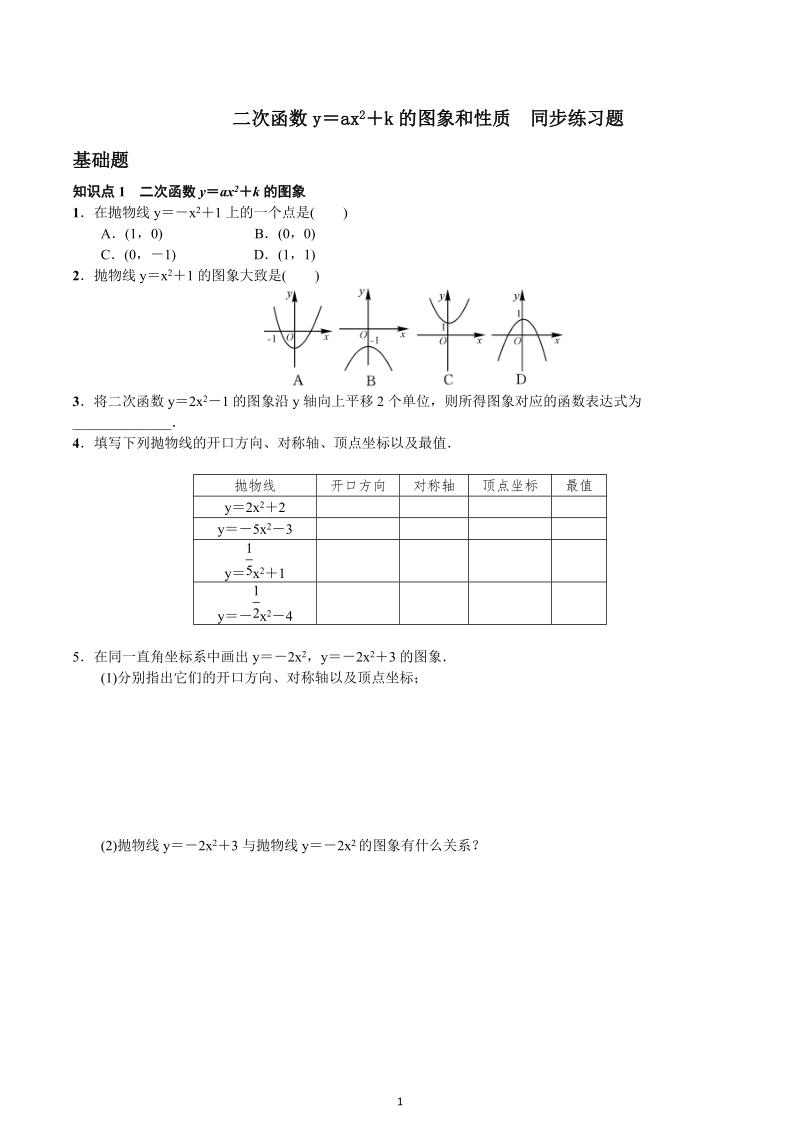
1、1二次函数 yax 2k 的图象和性质 同步练习题基础题知识点 1 二次函数 yax 2k 的图象1在抛物线 yx 21 上的一个点是( )A(1，0) B(0，0)C(0，1) D(1，1)2抛物线 yx 21 的图象大致是( )3将二次函数 y2x 21 的图象沿 y 轴向上平移 2 个单位，则所得图象对应的函数表达式为_4填写下列抛物线的开口方向、对称轴、顶点坐标以及最值抛物线 开口方向 对称轴 顶点坐标 最值y2x 22y5x 23y x2115y x24125在同一直角坐标系中画出 y2x 2，y2x 23 的图象(1)分别指出它们的开口方向、对称轴以及顶点坐标；(2)抛物线 y2x
2、 23 与抛物线 y2x 2 的图象有什么关系？2知识点 2 二次函数 yax 2k 的性质6已知点(x 1，y 1)，(x 2，y 2)均在抛物线 yx 21 上，下列说法中正确的是( )A若 y1y 2，则 x1x 2B若 x1x 2，则 y1y 2C若 0x 1x 2，则 y1y 2D若 x1x 20，则 y1y 27对于二次函数 y3x 22，下列说法错误的是( )A最小值为 2B图象与 y 轴没有公共点C当 x0 时，y 随 x 的增大而减小D其图象的对称轴是 y 轴8抛物线 y2x 21 在 y 轴右侧的部分是_( 填“上升”或“下降”) 9二次函数 y3x 23 的图象开口向_，
3、顶点坐标为_，对称轴为_，当 x0 时，y 随 x的增大而_；当 x0，所以 y 有最_值，当 x_时，y 的最_值是_中档题10下列各图象中有可能是函数 yax 2a(a0)的图象的是( )11在同一坐标系中，一次函数 ymx n 2 与二次函数 yx 2m 的图象可能是( )12已知 yax 2k 的图象上有三点 A(3，y 1)，B(1，y 2)，C(2，y 3)，且 y20 Ba0Ca 0 Da013与抛物线 y x21 顶点相同，形状也相同，而开口方向相反的抛物线所对应的函数解析式是( )45Ay x21 By x2154 45Cy x21 Dy x2145 4514若二次函数 ya
4、x 2c ，当 x 取 x1，x 2(x1x 2)时，函数值相等，则当 x 取 x1x 2 时，函数值为( )Aac Ba cCc Dc15将抛物线 yax 2c 向下平移 3 个单位，得到抛物线 y2x 21，则 a_，c_16若抛物线 yax 2k(a0)与 y2x 24 关于 x 轴对称，则 a_，k_317直接写出符合下列条件的抛物线 yax 21 的函数关系式：(1)通过点(3， 2)；(2)与 y x2 的开口大小相同，方向相反；12(3)当 x 的值由 0 增加到 2 时，函数值减少 4.18把 y x2 的图象向上平移 2 个单位12(1)求新图象的解析式、顶点坐标和对称轴；(
5、2)画出平移后的函数图象；(3)求平移后的函数的最大值或最小值，并求对应的 x 的值4综合题19如图，隧道的截图由抛物线和长方形构成，长方形的长是 8 m，宽是 2 m，抛物线可以用 y x2414表示一辆货运卡车高 4 m，宽 2 m，它能通过该隧道吗？5参考答案基础题1.A 2.C 3.y2x 21 4.向上 y 轴 (0，2) 最小值 2 向下 y 轴 (0，3) 最大值3 向上 y 轴 (0 ，1) 最小值 1 向下 y 轴 (0，4) 最大值4 5.如图所示. (1)抛物线 y2x 2 开口方向向下，对称轴为 y 轴，顶点坐标为 (0，0)抛物线 y2x 23 开口方向向下，对称轴为
6、 y 轴，顶点坐标为(0，3) (2)抛物线 y2x 23 可由抛物线 y2x 2 的图象向上平移 3 个单位得到 6.D 7.B 8.上升 9.上 (0，3) y 轴 增大 减小 小 0 小 3中档题10.B 11.D 12.A 13.B 14.D 15.2 2 16.2 4 17.(1)y x21.(2)y x21.(3)y x 21. 13 1218.(1)y x22，顶点坐标是(0 ，2)，对称轴是 y 轴(2)略(3)x 0 时，y 有最大值，为 2.12综合题19.把 y422 代入 y x24，得 2 x24，解得 x2 .此时可通过物体的宽度为14 14 22 (2 )4 2，它能通过该隧道2 2 2
