1、提分专练提分专练( (三三) ) 一次函数与反比例函数的综合一次函数与反比例函数的综合 |类型 1| 一次函数与反比例函数的综合 1.2018 襄阳 如图 T3-1,已知双曲线 y1= 与直线 y2=ax+b 交于点 A(-4,1)和点 B(m,-4). (1)求双曲线和直线的解析式; (2)直接写出线段 AB 的长和 y1y2时 x 的取值范围. 图 T3-1 2.2018 贵港 如图 T3-2,已知反比例函数 y= (x0)的图象与一次函数 y=- 1 2x+4 的图象交于 A 和 B(6,n)两点. (1)求 k 和 n 的值; (2)若点 C(x,y)也在反比例函数 y= (x0)的图
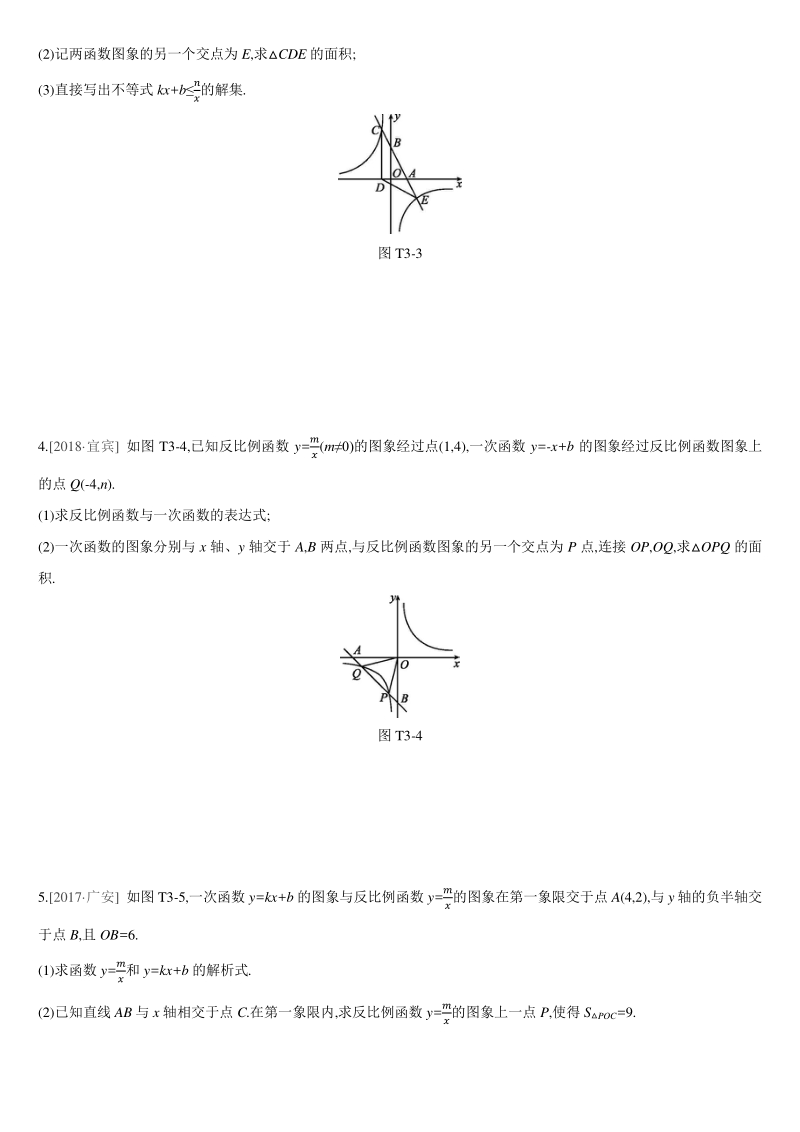
2、象上,求当 2x6 时,函数值 y 的取值范围. 图 T3-2 3.2018 枣庄 如图 T3-3,一次函数 y=kx+b(k,b 为常数,k0)的图象与 x 轴、 y 轴分别交于 A,B 两点,且与反比例函数 y= (n 为常数,且 n0)的图象在第二象限交于点 C,CDx 轴,垂足为 D,若 OB=2OA=3OD=12. (1)求一次函数与反比例函数的解析式; (2)记两函数图象的另一个交点为 E,求CDE 的面积; (3)直接写出不等式 kx+b 的解集. 图 T3-3 4.2018 宜宾 如图 T3-4,已知反比例函数 y= (m0)的图象经过点(1,4),一次函数 y=-x+b 的图
3、象经过反比例函数图象上 的点 Q(-4,n). (1)求反比例函数与一次函数的表达式; (2)一次函数的图象分别与 x 轴、y 轴交于 A,B 两点,与反比例函数图象的另一个交点为 P 点,连接 OP,OQ,求OPQ 的面 积. 图 T3-4 5.2017 广安 如图 T3-5,一次函数 y=kx+b 的图象与反比例函数 y= 的图象在第一象限交于点 A(4,2),与 y 轴的负半轴交 于点 B,且 OB=6. (1)求函数 y= 和 y=kx+b 的解析式. (2)已知直线 AB 与 x 轴相交于点 C.在第一象限内,求反比例函数 y= 的图象上一点 P,使得 S POC =9. 图 T3-
4、5 6.2018 北京 在平面直角坐标系 xOy 中,函数 y= (x0)的图象 G 经过点 A(4,1),直线 l:y= 1 4x+b 与图象 G 交于点 B,与 y 轴 交于点 C. (1)求 k 的值. (2)横、纵坐标都是整数的点叫做整点.记图象 G 在点 A,B 之间的部分与线段 OA,OC,BC 围成的区域(不含边界)为 W. 当 b=-1 时,直接写出区域 W 内的整点个数. 若区域 W 内恰有 4 个整点,结合图象,求 b 的取值范围. |类型 2| 反比例函数的实际应用 7.2018 乐山 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜,图 T3-6 是试
5、验阶段的某天恒 温系统从开启到关闭后,大棚内的温度 y()与时间 x(h)之间的函数关系,其中线段 AB,BC 表示恒温系统开启阶段,双曲线 的一部分 CD 表示恒温系统关闭阶段. 请根据图中信息解答下列问题: (1)求这天的温度 y 与时间 x(0 x24)的函数关系式; (2)求恒温系统设定的恒定温度; (3)若大棚内的温度低于 10,蔬菜会受到伤害,问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害? 图 T3-6 参考答案参考答案 1.解:(1)双曲线 y1= 经过点 A(-4,1), k=-41=-4,双曲线的解析式为 y1=-4 . 双曲线 y1=-4 经过点 B(m,
6、-4), -4m=-4,m=1,B(1,-4). 直线 y2=ax+b 经过点 A(-4,1)和点 B(1,-4), -4 + = 1, + = -4, 解得 = -1, = -3, 直线的解析式为 y2=-x-3. (2)AB=52,y1y2时,x 的取值范围是-4x1. 提示:由两点间距离坐标公式得 AB=(-4-1)2+ (1 + 4)2=52. 在图象中找出双曲线在直线上方的部分,确定这部分 x 的取值范围是-4x1. 2.解:(1)把 B(6,n)代入一次函数 y=-1 2x+4 中,可得 n=- 1 26+4=1, 所以 B 点的坐标为(6,1). 又 B 在反比例函数 y= (x
7、0)的图象上, 所以 k=xy=16=6, 所以 k 的值为 6,n 的值为 1. (2)由(1)知反比例函数的解析式为 y=6 . 当 x=2 时,y=6 2=3;当 x=6 时,y= 6 6=1, 由函数图象可知,当 2x6 时函数值 y 的取值范围是 1y3. 3.解:(1)OB=2OA=3OD=12, OA=6,OB=12,OD=4, A(6,0),B(0,12),点 D 的横坐标为-4, 把点 A,点 B 的坐标代入 y=kx+b 得 0=6k+b,b=12, k=-2,一次函数的解析式为 y=-2x+12. 点 C 与点 D 的横坐标相同,代入 y=-2x+12 得点 C 的纵坐标
8、为 20,即 C(-4,20), 20= -4,n=-80, 反比例函数的解析式为 y=-80 . (2)由 y=-2x+12 和 y=-80 得-2x+12=-80 , 解得 x1=-4,x2=10,E(10,-8), CDE 的面积为1 220(10+4)=140. (3)由图象可得-4x0). 在直线 y=2x-6 上,当 y=0 时,x=3, 点 C 的坐标为(3,0),即 OC=3, S POC =1 2OC yP= 1 23 8 =9, 解得 n=4 3,点 P 的坐标为 4 3,6 , 故当 S POC =9 时,在第一象限内,反比例函数 y=8 的图象上点 P 的坐标为 4 3
9、,6 . 6.解:(1)函数 y= (x0)的图象经过点 A(4,1), 1= 4,解得 k=4. (2)如图所示:由图可知区域 W 内的整点个数有 3 个:(1,0),(2,0),(3,0). 由可知,当直线 BC 过点(4,0)时,b=-1;当直线 BC 过点(5,0)时,5 4+b=0,b=- 5 4.此时,区域 W 内的整点个数有 4 个:(1,0),(2,0),(3,0),(4,0).结合函数图象知-5 4b-1. 当直线 BC 过点(1,2)时,1 4+b=2,b= 7 4. 当直线 BC 过点(1,3)时,1 4+b=3,b= 11 4 .此时,区域 W 内的整点个数有 4 个:
10、(1,1),(2,1),(3,1),(1,2).结合函数图象知7 4b 11 4 . 综上,-5 4b-1 或 7 4b 11 4 . 7.解:(1)设线段 AB 的解析式为 y=k1x+b(k10,0 x5). 线段 AB 过(0,10),(2,14), = 10, 21+ = 14,解得 1= 2, = 10, 线段 AB 的解析式为 y=2x+10(0 x5). B 在线段 AB 上,当 x=5 时,y=20, 点 B 的坐标为(5,20). 线段 BC 的解析式为 y=20(5x10). 设双曲线 CD 段的解析式为 y=2 (k20,10 x24), 点 C 在线段 BC 上, 点 C 的坐标为(10,20). 又点 C 在双曲线 y=2 上,k2=200. 双曲线 CD 段的解析式为 y=200 (10 x24). 故 y= 2 + 10(0 5), 20(5 10), 200 (10 24). (2)由(1)知,恒温系统设定的恒定温度为 20. (3)把 y=10 代入 y=200 中,解得 x=20, 20-10=10. 答:恒温系统最多关闭 10 小时,蔬菜才能避免受到伤害.
